大問1
(1) 次の➀~➃を計算しなさい。
➀ \( -5+1-(-12) \)
【解説】
\( =-5+1+12 \)
\( =8 \)
➁ \( \dfrac{3x+y}{2}-\dfrac{x+y}{3} \)
【解答】
\( \dfrac{7x+y}{6} \)
【解説】
\( =\dfrac{3(3x+y)-2(x+y)}{6} \)
\( =\dfrac{7x+y}{6} \)
➂ \( -ab^2 \div \dfrac{2}{3}a^2b \times (-4b) \)
【解答】
\( \dfrac{6b^2}{a} \)
【解説】
\( =\dfrac{-ab^2 \times 3 \times (-4b)}{2a^2b} \)
\( =\dfrac{6b^2}{a} \)
➃ \( \dfrac{8}{\sqrt{12}}+\sqrt{50} \div \sqrt{6} \)
【解説】
\( =\dfrac{8}{2\sqrt{3}}+\dfrac{5\sqrt{2}}{\sqrt{6}} \)
\( =\dfrac{4}{\sqrt{3}}+\dfrac{5}{\sqrt{3}} \)
\( =\dfrac{9}{\sqrt{3}} \)
\( =3\sqrt{3} \)
(2) ある中学校の生徒30人の通学時間を調べたところ,自転車で通学する23人の通学時間の平均値は \( a \) 分,徒歩で通学する7人の通学時間の平均値は \( b \) 分,生徒全員の通学時間の平均値は \( 14 \) 分であった。このとき,\( b \) を \( a \) の式で表しなさい。
【解答】
\( b=-\dfrac{23}{7}a+60 \)
【解説】
「平均値」=「すべてのデータの合計値」÷「データの個数」 の関係になっているので,
「すべてのデータの合計値」=「平均値」✕「データの個数」 になります。
生徒全員の通学時間の平均値は \( 14 \) 分なので,
生徒全員の通学時間の合計値は,\( 14 \times 30=420 \) 分 ・・・ ① になります。
自転車で通学する23人の通学時間の平均値は \( a \) 分なので,
自転車通学の人の通学時間の合計値は,\( a \times 23=23a \) 分 ・・・ ➁ になります。
徒歩で通学する7人の通学時間の平均値は \( b \) 分なので,
徒歩通学の人の通学時間の合計値は,\( b \times 7=7b \) 分 ・・・ ➂ になります。
➀➁➂より,
\( 23a+7b=420 \)
\( 7b=-23a+420 \)
\( b=-\dfrac{23}{7}a+60 \)
(3) 次の四角形のうち,必ず平行四辺形になる四角形はどれか。次のア~エからすべて選び,その記号を書きなさい。
ア 4つの角がすべて直角である四角形
イ 1組の対辺が平行であり,もう1組の対辺の長さが等しい四角形
ウ 対角線が垂直に交わる四角形
エ 対角線がそれぞれの中点で交わる四角形
【解説】
ア 4つの角がすべて直角である四角形は長方形になります。
長方形の対辺は平行で長さが等しいので,必ず平行四辺形になります。
イ 等脚台形は平行四辺形にはなりません。
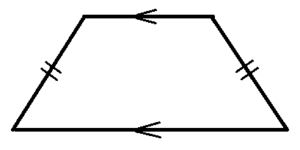
ウ 下の図のような図形は平行四辺形にはなりません。
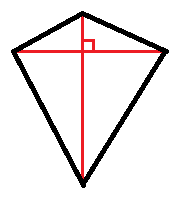
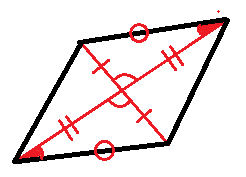
エ 対角線がそれぞれの中点で交わるとき,四角形の中にできる向かい合う三角形は,
2組の辺とその間の角がそれぞれ等しいので,合同になります。
合同な三角形において,対応する辺と角は等しいので,
この四角形は1組の対辺が平行で長さが等しくなり,必ず平行四辺形になります。
(4) \( 8a^2b-18b \) を因数分解しなさい。
【解答】
\( 2b(2a+3)(2a-3) \)
【解説】
\( =2b(4a^2-9) \)
\( =2b(2a+3)(2a-3) \)
(5) 2つの方程式 \( 3x+2y+16=0,2x-y+6=0 \) のグラフの交点が,方程式 \( ax+y+10=0 \) のグラフ上にある。このときの \( a \) の値を求めなさい。
【解説】
2つのグラフの交点は連立方程式の解として求めることができます。
\( 3x+2y+16=0,2x-y+6=0 \) を連立方程式として解くと,
\( x=-4,y=-2 \)
これを \( ax+y+10=0 \) に代入すると,
\( a \times (-4)+(-2)+10=0 \)
\( 4a=8 \)
\( a=2 \)
連立方程式の途中式
\( \left\{ \begin{array}{}
3x+2y+16=0 \; ・・・ \; ➀ \\
2x-y+6=0 \; ・・・ \; ➁ \end{array} \right. \)
➁\( \times 2 \) すると,
\( 4x-2y+12=0 \) ・・・ ➁’
➀\( + \)➁’
\( 7x+28=0 \)
\( x=-4 \)
➁に代入すると,
\( 2 \times (-4)-y+6=0 \)
\( -y-2=0 \)
\( y=-2 \)
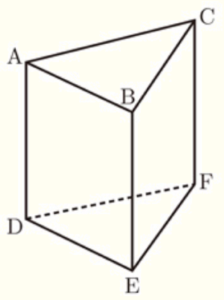
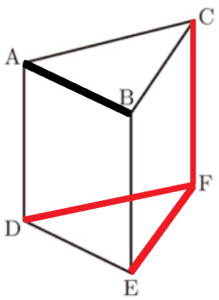
(6) 右の図は,三角柱 \( ABC-DEF \) である。辺 \( AB \) とねじれの位置にある辺をすべて書きなさい。
【解答】
辺 \( CF \),辺 \( DF \) ,辺 \( EF \)
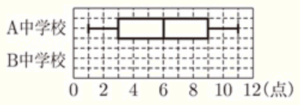
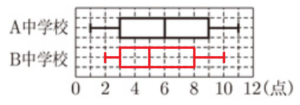
(7) 次の表は,A中学校とB中学校の野球部の最近10試合の得点のデータをまとめたものである。この表をもとに,A中学校の得点のデータを箱ひげ図で表した。A中学校の箱ひげ図にならって,B中学校の得点のデータの箱ひげ図をかき入れなさい。
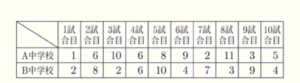
【解説】
B中学校の得点を少ない順に並べかえると,
\( 2,2,3,4,4,6,7,8,9,10 \)
このデータにおいて,最小値は,2点,最大値は10点
また,データの個数は10個だから,
第二四分位数(中央値)は,5番目と6番目の平均値になるので,5点
第一四分位数(中央値)は,3番目の値になるので,3点
第三四分位数(中央値)は,8番目の値になるので,8点
これらを箱ひげ図に表すと解答の図のようになります。
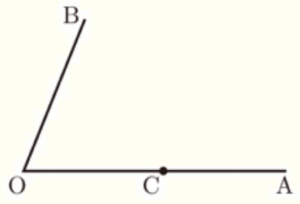
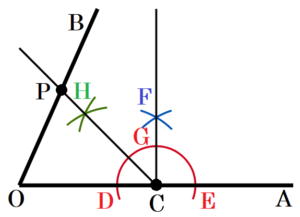
(8) 右の図のように,半直線 \( OA,OB \) があり,半直線 \( OA \) 上に点 \( C \) をとる。半直線 \( OB \) 上に \( ∠OCP=45° \) となる点 \( P \) を,定規とコンパスを使い,作図によって求めなさい。ただし,定規は直線をひくときに使い,長さを測ったり角度を利用したりしないこととする。なお,作図に使った線は消さずに残しておくこと。
【解答・解説】
点 \( C \) を通り,半直線 \( OA \) と垂直な直線を描き,そこでできる \( ∠C \) について二等分線を作図したとき,
半直線 \( OB \) の交点が求める点 \( P \) になります。
手順1 点 \( C \) を中心に円弧を描く
(半直線 \( OA \) との交点を点 \( D,E \) とします)
手順2 点 \( D,E \) を中心に円弧を描く
(交点を点 \( F \) とします)
手順3 半直線 \( CF \) を描く
(弧 \( DE \) との交点を点 \( G \) とします)
手順4 点 \( D,G \) を中心に円弧を描く
(交点を点 \( H \) とします)
手順5 半直線 \( CH \) を描く
手順5と半直線 \( OB \) との交点が求める点 \( P \) になります。
大問2
ゆうさんたちの学級では,数学の授業で次の〔問題〕に取り組んだ。下の【ゆうさんのノート】と【りくさんのノート】は,ゆうさんとりくさんがこの問題を正しく解いたノートの一部である。このことについて,下の (1)~(3) の問いに答えなさい。
〔問題〕
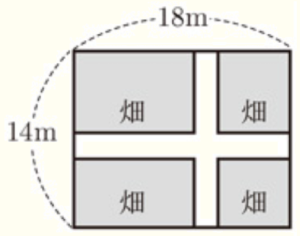
縦が \( 14 \; m \),横が \( 18 \; m \) の長方形の土地に,右の図のように,同じ幅の道を縦と横につくり,残りの土地を畑にすることにした。畑の面積が \( 192 \; m^2 \) となるようにするには,道幅を何 \( m \) にすればよいか。
【ゆうさんのノート】
〔解答〕
下の図のように,道を動かしても,畑の面積は
変わらない。
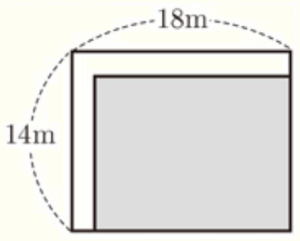
道幅を \( x \; m \) とすると,道を動かした畑の,
縦の長さと横の長さは,
( ア ) \( m \),( イ ) \( m \) と,
それぞれ \( x \) を使って表すことができる。
よって,方程式をつくると
( ア )( イ )\( =192 \)
\( ax^2+bx+c=0 \) の形にすると
X =0
Y
【りくさんのノート】
〔解答〕
道幅を \( x \; m \) とすると,縦方向の道の面積と横方向の道の面積は, ウ \( m^2 \),
エ \( m^2 \) と,それぞれ \( x \) を使って表すことができる。
また,縦方向の道と横方向の道が重なる部分の面積は \( x^2 \; m^2 \) となるので,道の面積の合計は,( ウ \( + \) エ \( -x^2) \; m^2 \) となる。
よって,方程式をつくると
\( 14×18-(\) ウ \( + \) エ \( -x^2)=192 \)
\( ax^2+bx+c=0 \) の形にすると
X =0
Y
(1) 【ゆうさんのノート】の ア , イ に当てはまる文字式を,それぞれ書きなさい。
【解答】
ア ・・・ \( 14-x \)
イ ・・・ \( 18-x \)
(2) 【りくさんのノート】の ウ , エ に当てはまる文字式を,それぞれ書きなさい。
【解答】
ウ ・・・ \( 14x \)
エ ・・・ \( 18x \)
(3) 【ゆうさんのノート】と【りくさんのノート】の X には同じ文字式が入り, Y には言葉と式を使って書いた解答の続きが入る。 X に当てはまる文字式と, Y に入る内容を書き,解答を完成させなさい。
【解答】
X ・・・ \( x^2-32x+60 \)
Y
\( (x-2)(x-30)=0 \)
\( x=2,30 \)
\( 0<x<14 \) より,あてはまるのは,\( x=2 \)
よって,道幅は \( 2 \; m \) にすればよい。
大問3
次の図のように,玉が6個入った箱Aと,玉が5個入った箱Bがある。1個のさいころを2回投げて,1回目に出た目の数だけ玉を箱Aから箱Bに移し,2回目に出た目の数だけ玉を箱Bから箱Aに移す。このとき,下の (1)・(2) の問いに答えなさい。ただし,さいころはどの目が出ることも同様に確からしいとする。

(1) 箱Aに入っている玉の個数が,5個になる確率を求めなさい。
【解説】
2回玉を移動させた後,箱Aの玉が1個減ればいいので,1回目に出た目の数が2回目に出た目の数より1大きければいいということになります。
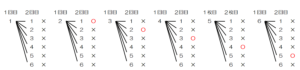
よって,出た目の組み合わせを樹形図に表すと,
あてはあまるのは5通り,すべての場合の数は36通りなので,求める確率は,\( \dfrac{5}{36} \)
(2) 箱Aに入っている玉の個数が,箱Bに入っている玉の個数より多くなる確率を求めなさい。
【解説】
1回目に移す玉の数と2回目に移す玉の数の大小関係によって,箱Aの玉の数と箱Bの玉の数の大小関係がどのようになるか考えると,
「1回目に移す玉の数」\( > \)「2回目に移す玉の数」のとき,「箱A」\( < \)「箱B」
「1回目に移す玉の数」\( = \)「2回目に移す玉の数」のとき,「箱A」\( > \)「箱B」
「1回目に移す玉の数」\( < \)「2回目に移す玉の数」のとき,「箱A」\( > \)「箱B」
なので,「1回目に移す玉の数」が「2回目に移す玉の数」と同じまたは少なくなる確率を求めます。
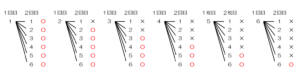
「1回目に移す玉の数」が「2回目に移す玉の数」と同じまたは少なくなるのは21通り,
すべての場合の数は36通りなので,求める確率は \( \dfrac{21}{36}=\dfrac{7}{12} \)
大問4
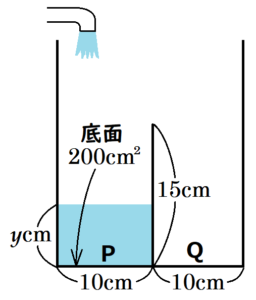
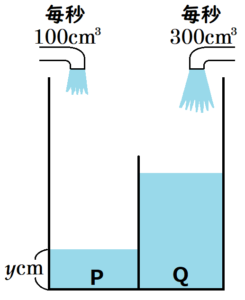
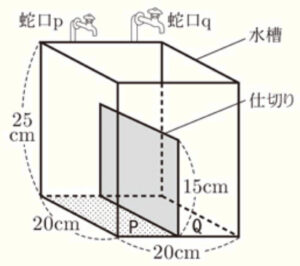
次の図のように,底面が1辺 \( 20 \; cm \) の正方形で高さが \( 25 \; cm \) である直方体の形をした水槽に,高さ \( 15 \; cm \) の長方形の仕切りが底面に対して垂直に取り付けられている。仕切りは底面積を2等分するように取り付けられており,2等分された底面をそれぞれ面 \( P \),面 \( Q \) とする。また,水槽の上には蛇口 \( p \),蛇口 \( q \) があり,蛇口 \( p \) を開くと面 \( P \) 側に水が入り,蛇口 \( q \) を開くと面 \( Q \) 側に水が入る。水面が仕切りの高さまで上昇すると,水があふれ出て仕切りの隣側に入る。水を入れ始めてから \( x \) 秒後の,面 \( P \) 側の水面の高さを \( y \; cm \) とするとき,下の (1)・(2)の問いに答えなさい。
ただし,水槽は水平な床の上に置かれており,水槽の壁や仕切りの厚さは考えないものとする。
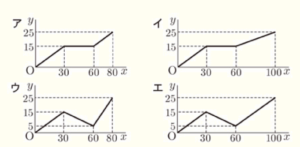
(1) 蛇口 \( p \) を開くと面 \( P \) 側に毎秒 \( 100 \; cm^3 \) ずつ水が入る。このとき,\( x \) と \( y \) との関係を表したグラフとして適切なものを,次のア~エから1つ選び,その記号を書きなさい。
【解説】
➀
面 \( P \) 側の底面積は \( 200 \; cm^2 \) なので,毎秒 \( 100 \; cm^3 \) ずつ水を入れるとき,毎秒 \( \dfrac{100}{200}=\dfrac{1}{2} \; (cm) \) ずつ水面の位置が高くなります。
仕切りの高さは \( 15 \; cm \) なので,\( x=15 \div \dfrac{1}{2}=30 \) 秒後に面 \( P \) 側が満タンになります。
➁
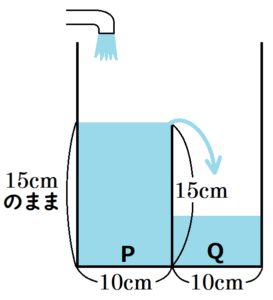
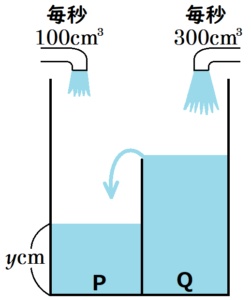
その後は,面 \( P \) 側からあふれる水が面 \( Q \) 側に入っていきます。
面 \( P \) 側と面 \( Q \) 側の容積は等しいので,面 \( Q \) 側が満タンになるまで \( 30 \) 秒かかります。
この \( x=30 \) から \( x=60 \) の間,面 \( P \) 側の水面の高さは \( 15 \; cm \) のままです。
➂
\( P \) 側も\( Q \) 側も仕切りの高さまで水が入った後は,水そう全体に水面の高さが高くなっていきます。
仕切りがなくなって,底面積は \( 400 \; cm^2 \) なので,毎秒 \( 100 \; cm^3 \) ずつ水を入れるとき,
毎秒 \( \dfrac{100}{400}=\dfrac{1}{4} \; cm \) ずつ水面の位置が高くなります。
仕切りがない部分の高さ \( 10 \; cm \) 水面が高くなるのにかかる時間は \( 10 \div \dfrac{1}{4}=40 \) 秒なので,水そうが満タンになるのは \( x=100 \) のときです。
以上を表しているグラフは イ になります。
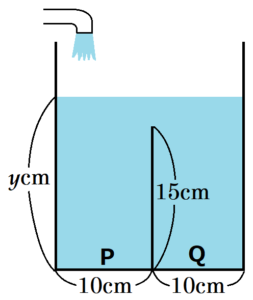
(2) 蛇口 \( p \) と蛇口 \( q \) の両方を同時に開けると,蛇口 \( p \) から面 \( P \) 側に毎秒 \( 100 \; cm^3 \) ずつ水が入り,蛇口 \( q \) から面 \( Q \) 側に毎秒 \( 300 \; cm^3 \) ずつ水が入る。このとき,次の➀・➁の問いに答えなさい。
➀ \( x=12 \) のときの \( y \) の値を求めなさい。
【解説】
面 \( Q \) 側には毎秒 \( 300 \; cm^3 \) ずつ水が入るので,
毎秒 \( \dfrac{300}{200}=\dfrac{3}{2} \; (cm) \) ずつ水面の位置が高くなります。
仕切りの高さは \( 15 \; cm \) なので,
\( x=15 \div \dfrac{3}{2}=10 \) 秒後に面 \( Q \) 側が満タンになります。
\( x=10 \) から \( x=12 \) までの \( 2 \) 秒間は,
蛇口 \( p \) からの毎秒 \( 100 \; cm^3 \) に加えて,
面 \( Q \) 側からあふれた毎秒 \( 300 \; cm^3 \) の合計で
毎秒 \( 400 \; cm^3 \) が面 \( P \) 側に入ります。
このとき,
毎秒 \( \dfrac{400}{200}=2 \; (cm) \) ずつ水面の位置が高くなります。
よって,
\( x=0 \) から \( x=10 \) までは,毎秒 \( \dfrac{1}{2} \; cm \) ずつ,
\( x=10 \) から \( x=12 \) までは,毎秒 \( 2 \; cm \) ずつ
面 \( P \) 側の水面の位置が高くなるので,\( x=12 \) のときの水面の位置は,
\( \dfrac{1}{2} \times 10+2 \times 2=9 \; (cm) \)
➁ \( x \) の値が \( 0 \) から \( 10 \) まで増加するときの変化の割合を \( a \),\( 10 \) から \( 15 \) まで増加するときの変化の割合を \( b \),\( 15 \) から \( 25 \) まで増加するときの変化の割合を \( c \) とするとき,\( a,b,c \) の大小を,不等号を使って表しなさい。
【解説】
変化の割合は毎秒何 \( cm \) ずつ水面の位置が高くなるかを表しています。
【\( x=0 \) から \( x=10 \) まで】
(1) と (2)➀ より,変化の割合は,\( a=\dfrac{1}{2} \)
【\( x=10 \) から \( x=15 \) まで】
(2)➀ より,面 \( P \) 側が満タンになるのが \( t \) 秒後とすると,
\( \dfrac{1}{2} \times 10+2 \times (t-10)=15 \; (cm) \)
\( 2t-15=15 \; (cm) \)
\( t=15 \) (秒後)
ここから,\( x=10 \) から \( x=15 \) まで増加するときの変化の割合は,\( b=2 \)
【\( x=15 \) から \( x=25 \) まで】
\( x=15 \) から後は,底面積 \( 400 \; cm^2 \) の水槽に毎秒 \( 400 \; cm^3 \) ずつ水を入れるので,
毎秒 \( \dfrac{400}{400}=1 \; cm \) ずつ水面の位置が高くなります。
ここから,水面の位置が \( 10 \; cm \) 高くなるのにかかる時間は \( 10 \) 秒です。
よって,\( x=15 \) から \( x=25 \) まで増加するときの変化の割合は,\( c=1 \)
以上より,\( a,b,c \) の大小の関係は,\( a<c<b \)
大問5
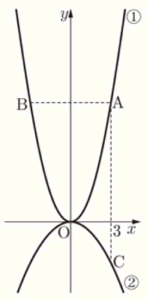
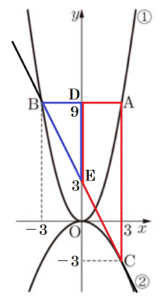
右の図において,➀は関数 \( y=x^2 \) のグラフ,➁は \( y=-\dfrac{1}{3}x^2 \) のグラフである。点 \( A \) は➀のグラフ上にあり,\( x \) 座標は \( 3 \) である。点 \( A \) と \( y \) 軸について対称な点を \( B \) とし,点 \( A \) と \( x \) 座標が等しい➁のグラフ上の点を \( C \) とする。このとき,次の (1)~(3) の問いに答えなさい。
(1) 点 \( C \) の座標を求めなさい。
【解説】
\( y=-\dfrac{1}{3}x^2 \) に \( x=3 \) を代入すると,
\( y=-\dfrac{1}{3} \times 3^2=-3 \)
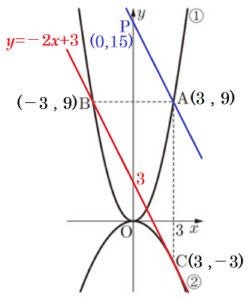
(2) 直線 \( BC \) と傾きが等しく,点 \( A \) を通る直線と,\( y \) 軸との交点を \( P \) とする。このとき,三角形 \( PBC \) の面積を求めなさい。
【解説】
点 \( A,B,C \) の座標は \( A(3,9),B(-3,9),C(3,-3) \) なので,
直線 \( BC \) の傾きは,\( \dfrac{-3-9}{3-(-3)}=-2 \)
直線 \( BC \) の式を \( y=-2x+b \) とすると,\( (3,-3) \) を通るので,
\( -3=-2 \times 3+b \)
\( b=3 \)
よって,直線 \( BC \) の式は \( y=-2x+3 \)
直線 \( AP \) の式を \( y=-2x+c \) とすると,\( (3,9) \) を通るので,
\( 9=-2 \times 3+c \)
\( c=15 \)
よって,点 \( P \) の座標は \( P(0,15) \)
直線 \( BC \) と\( y \) 軸との交点を \( Q \) とすると,
\( △PBC=△PBQ+△PCQ \) と考えることができます。
\( △PBQ,△PCQ \) の辺 \( PQ \) を底辺とすると,
どちらの三角形も底辺 \( PQ=12 \),高さは \( 3 \) なので,
\( △PBC=△PBQ+△PCQ \)
\( =12 \times 3 \times \dfrac{1}{2}+12 \times 3 \times \dfrac{1}{2} \)
\( =36 \)
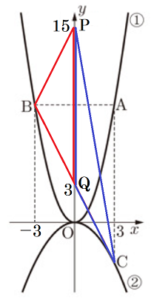
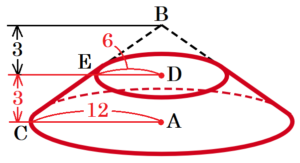
(3) 線分 \( AB \) と \( y \) 軸との交点を \( D \),線分 \( BC \) と \( y \) 軸との交点を \( E \) とする。台形 \( DECA \) を線分 \( DA \) を軸として1回転させたときにできる立体の体積を求めなさい。
ただし,円周率は \( \pi \) を用いること。
【解説】
台形 \( DECA \) は,\( △BAC \) から \( △BDE \) を除いたものなので,
体積を求める立体は,
「頂点が \( B \) で底面が線分 \( AC \) を半径とする円である円すい」から
「頂点が \( B \) で底面が線分 \( DE \) を半径とする円である円すい」を取り除いたものになります。
つまり,
求める立体 \(=\) 「大きい円すい」 \(-\) 「小さい円すい」
になります。
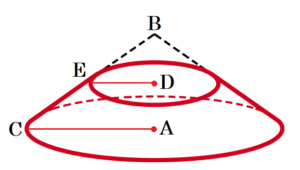
点 \( A,C,D,E \) の座標は,\( A(3,9),C(3,-3),
D(0,9),E(0,3) \) なので,
\( AC=12,DE=6 \),
大きい円すいの高さは \( 6 \),
小さい円すいの高さは \( 3 \)
になります。
大きい円すいの体積は,
\( \pi \times 12^2 \times 6 \times \dfrac{1}{3}=288\pi \)
小さい円すいの体積は,
\( \pi \times 6^2 \times 3 \times \dfrac{1}{3}=36\pi \)
よって,求める立体の体積は,
\( 288\pi-36\pi=252\pi \)
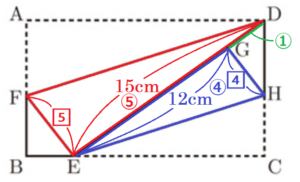
大問6
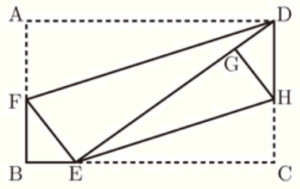
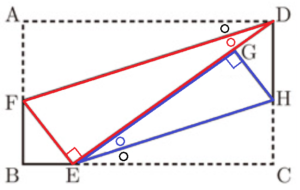
右の図のように,\( AB<BC \) であるような長方形 \( ABCD \) がある。まず,折り目が頂点 \( D \) を通り,頂点 \( A \) が辺 \( BC \) 上にくるように折り返す。このとき,頂点 \( A \) が移った点を \( E \) とし,折り目を線分 \( DF \) とする。次に,折り目が点 \( E \) を通り,頂点 \( C \) が線分 \( DE \) 上にくるように折り返す。このとき,頂点 \( C \) が移った点を \( G \) とし,折り目を線分 \( EH \) とする。次の (1)・(2) の問いに答えなさい。
(1) \( △DFE \) ∽ \( △EHG \) を証明しなさい。
【解答】
\( △DFE \) と \( △EHG \) において
長方形のすべての内角は \( 90° \) なので,
\( ∠DEF=∠EGH \) ・・・ ➀
長方形の向かい合う辺は平行なので,
\( ∠ADE=∠CEG \) ・・・ ➁
折り返す前後の図形は合同なので,
\( △ADF≡△EDF,△CEH≡△GEH \)
合同な三角形の対応する角の大きさは等しいので,
\( ∠EDF=\dfrac{1}{2}∠ADE \) ・・・ ➂
\( ∠GEH=\dfrac{1}{2}∠CEG \) ・・・ ➃
➁➂➃より,\( ∠EDF=∠GEH \) ・・・ ➄
➀➄より,2組の角がそれぞれ等しいので,\( △DFE \) ∽ \( △EHG \)
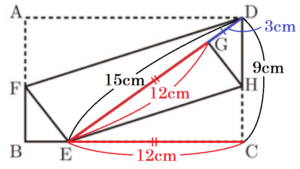
(2) \( AB=9 \; cm,BC=15 \; cm \) のとき,三角形 \( DFE \) の面積は,三角形 \( DHG \) の面積の何倍か。
【解答】
\( \dfrac{25}{4} \) 倍
【解説】
\( △DEC \) において,
\( CD=AB=9 \; cm,DE=BC=15 \; cm \)より,
\( BC^2=DE^2-CD^2=15^2-9^2=144 \)
\( BC=12 \; (cm) \) (\(BC>0\) より)
\( DE=15 \; cm,EG=BC=12 \; cm \) より,
\( DG=DE-EG=3 \; cm \)
(1) より,\( △DFE \) ∽ \( △EHG \) なので,
\( EF:GH=DE:EG=15:12=5:4 \)
\( EF=\dfrac{5}{4}GH \)
\( DE=15 \; cm,DG=3 \; cm \) より,
\( DE=5DG \)
よって,
\( △DFE=DE \times EF \times \dfrac{1}{2} \)
\( =5DG \times \dfrac{5}{4}GH \times \dfrac{1}{2} \)
\( =\dfrac{25}{4}\left(DG \times GH \times \dfrac{1}{2}\right) \)
\( △DFE=DG \times GH \times \dfrac{1}{2} \) なので,
\( △DFE=\dfrac{25}{4}△DFE \)