大問1
(1) \( -1+7 \)
(2) \( (-8) \times (-2)-(-4) \)
【解説】
\( =16+4 \)
\( =20 \)
(3) \( (-3a-5)-(5-3a) \)
【解説】
\( =-3a-5-5+3a \)
\( =-10 \)
(4) \( 4a^2b \div \dfrac{3}{2}b \)
【解答】
\( \dfrac{8}{3}a^2 \)
【解説】
\( =4a^2b \times \dfrac{2}{3b} \)
\( =\dfrac{8}{3}a^2 \)
(5) \( (\sqrt{3}+2)(\sqrt{3}-5) \)
【解説】
\( =3-5\sqrt{3}+2\sqrt{3}-10 \)
\( =-7-3\sqrt{3} \)
(6) ある正の整数から \( 3 \) をひいて,これを2乗すると \( 64 \) になります。この正の整数を求めなさい。ただし,解答欄の書き出しに続けて,答えを求めるまでの過程も書きなさい。
【解説】
ある正の整数を \( x \) とすると,
\( (x-3)^2=64 \)
\( x-3=±8 \)
\( x=3±8 \)
\( x=11,-5 \)
\( x \) は正の整数なので,あてはまるのは,\( x=11 \)
(7) \( y \) は \( x \) に反比例し,\( x=-3 \) のとき \( y=1 \) です。このとき,\( y \) を \( x \) の式で表しなさい。
【解答】
\( y=-\dfrac{3}{x} \)
【解説】
反比例の式は \( y=\dfrac{a}{x} \) (\( a \) は定数) で表すことができます。
\( x=-3 \) のとき \( y=1 \) なので,この式に代入すると,
\( 1=\dfrac{a}{-3} \)
\( a=-3 \)
よって,この式は,\( y=-\dfrac{3}{x} \)
(8) ことがらAの起こる確率を \( p \) とするとき,ことがらAの起こらない確率を \( p \) を使って表しなさい。
【解説】
確率とは,絶対に起こるを \( 1 \),絶対に起こらないを \( 0 \) として表すので,
起こる確率と起こらない確率の和は必ず1になります。
(9) 次のことがらが正しいかどうかを調べて,正しい場合には解答欄に「正しい」と書き,正しくない場合には反例を一つ書きなさい。
\( a \) が \( 3 \) の倍数ならば,\( a \) は\( 6 \) の倍数である。
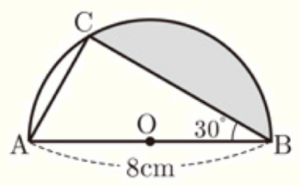
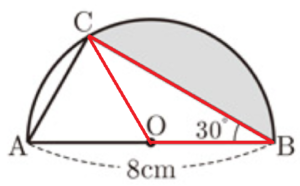
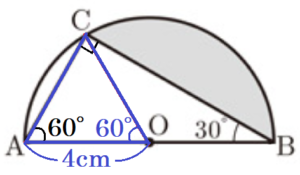
(10) 図のように,線分 \( AB \) を直径とする半円 \( O \) の弧 \( AB \) 上に点 \( C \) があります。3点 \( A,B,C \) を結んでできる \( △ABC \) について,\( AB=8 \; cm,∠ABC=30° \) のとき,弧 \( BC \) と線分 \( BC \) で囲まれた色のついた部分の面積を求めなさい。
【解答】
\( \dfrac{16}{3}\pi{}-4\sqrt{3} \; cm^2 \)
【解説】
補助線 \( OC \) をひくと,色がついた部分の面積は,
おうぎ形 \( OBC-△OBC \)
で求めることができます。
【\( △OBC \) の面積】
\( △ABC \) において,直径に対する円周角なので,\( ∠ACB=90° \)
ここから,\( ∠BAC=180°-30°-90°=60° \)
\( △OAC \) において,どちらも半径なので,\( OA=OC \) であり,
1つの角が \( 60° \) の二等辺三角形なので,正三角形になっています。
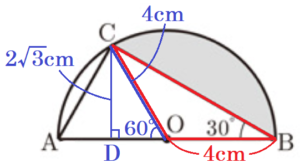
点 \( C \) から線分 \( AB \) に垂線をひき,交点を点 \( D \) とすると,
\( △OBC \) は,底辺 \( OB \),高さ \( CD \) であると考えられます。
\( △OCD \) は,\( 30°,60°,90° \) の直角三角形なので,
\( CD=OC \times \dfrac{\sqrt{3}}{2}=2\sqrt{3} \; (cm) \)
よって,
\( △OBC=4 \times 2\sqrt{3} \times \dfrac{1}{2}=4\sqrt{3} \; (cm^2) \)
おうぎ形 \( OBC \) の面積は,
半円 \( O=\pi{} \times 4 \times 4 \times \dfrac{120°}{360°}=\dfrac{16}{3}\pi{} \; (cm^2) \)
なので,
色がついた部分の面積 \( =\dfrac{16}{3}\pi{}-4\sqrt{3} \; (cm^2) \)
大問2
太郎さんと花子さんは,中学生の体力について調べています。<会話>を読んで,(1)〜(3) に答えなさい。
<会話>
太郎:私たちの中学校で実施している2年生の体力テストの結果を,5年ごとに比較してみよう。
花子:(あ)2010年,2015年,2020年の50m走のデータをもとに,箱ひげ図を作ってみたよ。
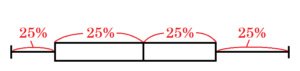
太郎:箱ひげ図の箱で示された区間には,すべてのデータのうち,真ん中に集まる約 (い) % のデータが
含まれていたよね。 箱ひげ図は,複数のデータの分布を比較しやすいね。
花子:(う)2010年,2015年,2020年の50m走のデータをもとに,ヒストグラムも作ってみたよ。
太郎:箱ひげ図とヒストグラムを並べると,データの分布をより詳しく比較できるね。
次は,反復横とびのデータを比較してみようよ。
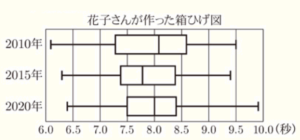
(1) 下線部 (あ) について,花子さんが作った箱ひげ図から読み取れることとして,次の ➀,➁ のことがらは,それぞれ正しいといえますか。【選択肢】の ア〜ウ の中から最も適当なものをそれぞれ一つ答えなさい。
➀ 2015年の第3四分位数は,2010年の第3四分位数よりも小さい。
➁ 2020年の平均値は8.0秒である。
【選択肢】
ア 正しい イ 正しくない ウ 花子さんが作った箱ひげ図からはわからない
【解説】
➀ 2015年の第3四分位数は,約8.4回,2010年の第3四分位数は,約8.6回
➁ 箱ひげ図からだけでは平均値は求められません。
(2) (い) に当てはまる数として最も適当なのは,ア~エ のうちではどれですか。一つ答えなさい。
ア \( 25 \) イ \( 50 \) ウ \( 75 \) エ \( 100 \)
【解説】
上下のひげの部分,第二四分位数をはさんで箱の左右には,それぞれ約 \( 25 \)%のデータが含まれます。
よって,箱の部分全体では約 \( 50 \)%のデータが含まれることになります。
(3) 下線部 (う) について,次の3つのヒストグラムは,花子さんが作った箱ひげ図の2010年,2015年,2020年のいずれかに対応しています。各年の箱ひげ図に対応するヒストグラムを,ア〜ウ の中からそれぞれ一つ答えなさい。
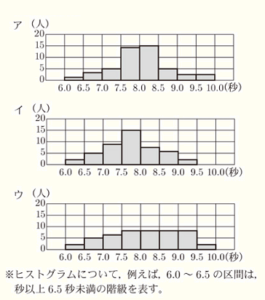
【解答】
2010年 ・・・ ウ
2015年 ・・・ イ
2020年 ・・・ ア
【解説】
まず,箱ひげ図とヒストグラムから,
最大値が9.0秒以上9.5秒未満の介入に含まれている2015年が イ になります。
次に,ア のヒストグラムに注目すると,
ほとんどの人が7.5秒以上8.0秒未満と8.0秒以上8.5秒未満の階級に含まれていることがわかります。
ここから,箱ひげ図の箱の部分全体が7.5秒以上8.5秒未満の範囲の中に含まれている
2020年がこれにあたることがわかります。
大問3
太郎さんは,ある洋菓子店で \( 1500 \) 円分の洋菓子を買おうと考えています。
(1),(2) に答えなさい。 ただし,消費税は考えないものとします。

(1) 洋菓子店では,\( 1500 \) 円すべてを使い切ると,\( 1 \) 個 \( 180 \) 円のプリンと \( 1 \) 個 \( 120 \) 円のシュークリームを合わせて \( 9 \) 個買うことができます。➀,➁ に答えなさい。
➀ 次の数量の間の関係を等式で表しなさい。
\( 1 \) 個 \( 180 \) 円のプリンを \( x \) 個と \( 1 \) 個 \( 120 \) 円のシュークリームを \( y \) 個買うときの代金の合計が \( 1500 \) 円である。
【解答】
\( 180x+120y=1500 \)
【解説】
\( 1 \) 個 \( 180 \) 円のプリンを \( x \) 個買うときの代金は,\( 180x \) 円,
\( 1 \) 個 \( 120 \) 円のシュークリームを \( y \) 個買うときの代金は,\( 120y \) 円
これらの合計が \( 1500 \) 円なので,\( 180x+120y=1500 \)
➁ プリンとシュークリームをそれぞれ何個買うことができるかを求めなさい。
【解答】
プリン ・・・ \( 7 \) 個
シュークリーム ・・・ \( 2 \) 個
【解説】
買うことができるプリンの数を \( x \) 個,シュークリームの数を \( y \) 個とすると,
買うことができる個数の関係は \( x+y=9 \) なので,
\( \left\{ \begin{array}{}
180x+120y=1500 \; ・・・ \; ➀ \\
x+y=9 \; ・・・ \; ➁ \\
\end{array} \right. \)
➀より,
\( 6x+4y=50 \) ・・・ ➀’
➀’\( – \)➁\( \times 4 \)
\( 2x=14 \)
\( x=7 \)
①に代入すると,
\( 7+y=9 \)
\( y=2 \)
(2) 太郎さんが洋菓子店に行くと,プリンが売り切れていたので,代わりに \( 1 \) 個 \( 120 \) 円のシュークリームと \( 1 \) 個 \( 90 \) 円のドーナツを,\( 1500 \) 円すべてを使い切って買うことにしました。➀,➁ に答えなさい。
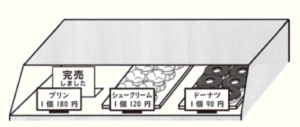
➀ 太郎さんは,シュークリームとドーナツをそれぞれ何個か買い,代金の合計が \( 1500 \) 円になる買い方について,次のように考えました。 には同じ数が入ります。 に適当な数を書きなさい。
<太郎さんの考え>
まず,次の数量の間の関係を等式で表します。
\( 1 \) 個 \( 120 \) 円のシュークリームを \( a \) 個と \( 1 \) 個 \( 90 \) 円のドーナツを \( b \) 個買うときの代金の合計が \( 1500 \) 円である。
次に,この等式を満たす \( a,b \) がどちらも \( 0 \) 以上の整数である場合を考えます。そのような \( a,b \) の組は,全部で 組あります。
よって,シュークリームとドーナツをそれぞれ何個か買い,代金の合計が \( 1500 \) 円になるような買い方は,全部で 通りあります。
【解説】
代金の関係式は \( 120a+90b=1500 \) なので,これを整理すると,\( b=50-\dfrac{4}{3}a \)
ここで,\( a \) が取り得る値の範囲は \( 0≦a≦12 \) なので,
\( a=0 \) のとき,\( b \) の値は,\( b=\dfrac{50}{3} \) → 整数ではないので不適
\( a=1 \) のとき,\( b \) の値は,\( b=\dfrac{46}{3} \) → 整数ではないので不適
\( a=2 \) のとき,\( b \) の値は,\( b=14 \) → ○
\( a=3 \) のとき,\( b \) の値は,\( b=\dfrac{38}{3} \) → 整数ではないので不適
\( a=4 \) のとき,\( b \) の値は,\( b=\dfrac{34}{3} \) → 整数ではないので不適
\( a=5 \) のとき,\( b \) の値は,\( b=10 \) → ○
\( a=6 \) のとき,\( b \) の値は,\( b=\dfrac{26}{3} \) → 整数ではないので不適
\( a=7 \) のとき,\( b \) の値は,\( b=\dfrac{22}{3} \) → 整数ではないので不適
\( a=8 \) のとき,\( b \) の値は,\( b=6 \) → ○
\( a=9 \) のとき,\( b \) の値は,\( b=\dfrac{14}{3} \) → 整数ではないので不適
\( a=10 \) のとき,\( b \) の値は,\( b=\dfrac{10}{3} \) → 整数ではないので不適
\( a=11 \) のとき,\( b \) の値は,\( b=2 \) → ○
\( a=12 \) のとき,\( b \) の値は,\( b=\dfrac{2}{3} \) → 整数ではないので不適
➁ シュークリームとドーナツがどちらも \( 8 \) 個ずつ残っているとき,それぞれ何個買うことができるかを求めなさい。
【解答】
シュークリーム ・・・ \( 8 \) 個
ドーナツ ・・・ \( 6 \) 個
【解説】
① の4通りのうち,\( 0≦a≦8,0≦b≦8 \) を満たすのは,\( a=8,b=6 \) の場合のみです。
大問4
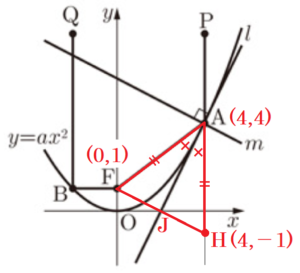
太郎さんは,パラボラアンテナに放物線の性質が利用されていることを知り,放物線について考えています。
<太郎さんが興味を持った性質>
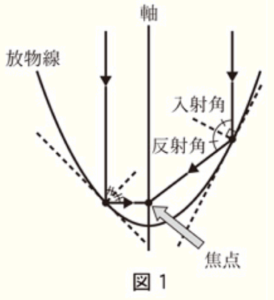
パラボラアンテナの形は,放物線を,その軸を回転の軸として回転させてできる曲面です。この曲面には,図1の断面図のように軸に平行に入ってきた光や電波を,ある1点に集めるという性質があります。
この点のことを 焦点 といいます。
また,光や電波がこの曲面で反射するとき,
入射角 \( = \) 反射角
となります。
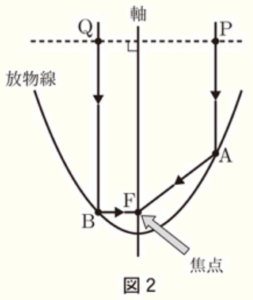
このとき,図2のように,点 \( P \) や点 \( Q \) を同時に通過した光や電波は、曲面上の点 \( A \) や点 \( B \) で反射し,同時に焦点 \( F \) に到達します。光や電波の進む速さは一定なので,
\( PA+AF=QB+BF \)
が成り立ちます。このことは,光や電波が,図2の破線上のどの位置を通過しても成り立ちます。
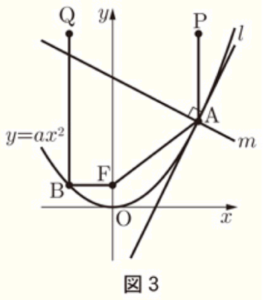
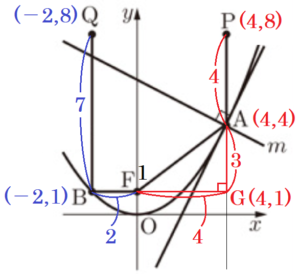
図3は,<太郎さんが興味を持った性質> を座標平面上に表したものです。 図3と【図3の説明】をもとに,(1)~(3) に答えなさい。
【図3の説明】
・2点 \( A,B \) は関数 \( y=ax^2 \) (\( a \) は定数) の
グラフ上の点
・点 \( A \) の座標は \( (4,4) \)
・点 \( B \) の \( x \) 座標は \( -2 \)
・点 \( F \) の座標は \( (0,1) \)
・点 \( P \) の座標は \( (4,8) \)
・点 \( Q \) の座標は \( (-2,8) \)
・直線 \( m \) は \( ∠PAF \) の二等分線
・直線 \( l \) は点 \( A \) を通り、直線 \( m \) と垂直に
交わる直線
・点 \( O \) は原点
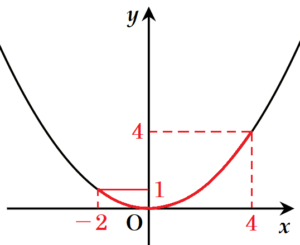
(1) 関数 \( y=ax^2 \) について,➀,➁ に答えなさい。
➀ \( a \) の値を求めなさい。
【解答】
\( a=\dfrac{1}{4} \)
【解説】
点 \( A(4,4) \) を通るので,
\( 4=a \times 4^2 \)
\( a=\dfrac{1}{4} \)
➁ \( x \) の変域が \( -2≦x≦4 \) のとき,\( y \) の変域を求めなさい。
【解説】
\( x \) の変域が \( 0 \) を含んでいるので,\( y \) の変域の最小値は \( 0 \)
\( x \) の変域の中で絶対値が最も大きくなるのは \( x=4 \) のときなので,
\( y \) の値は,\( y=\dfrac{1}{4} \times 4^2=4 \)
以上より,\( y \) の変域は,\( 0≦y≦4 \)
(2) 次の には \( 8 \) より小さい同じ数が入ります。 に適当な数を書きなさい。
\( PA+AF \) の値は,点 \( P \) と点 \( (4, \) \( ) \) の間の距離と等しい。
\( QB+BF \) の値は,点 \( Q \) と点 \( (-2, \) \( ) \) の間の距離と等しい。
【解説】
【\( PA+AF \) の値】
点 \( F \) から直線 \( PA \) に垂線をひき,
交点を点 \( G \) とすると,
\( AG=3,FG=4 \) なので,三平方の定理より,
\( AF^2=3^2+4^2=25 \)
\( AF=5 \) (\( AF>0 \) より)
求める点は点 \( A(4,4) \) から \( y \) 方向に \( -5 \) だけ
進んだ点なので,\( (4,-1) \) になります。
【\( QB+BF \) の値】
点 \( B \) は \( y=\dfrac{1}{4}x^2 \) 上の点で,\( x=-2 \) なので,
\( y \) 座標の値は,\( y=\dfrac{1}{4} \times (-2)^2=1 \)
ここから, \( B(-2,1),F(0,1) \) なので,\( BF=2 \)
求める点は点 \( B(-2,1) \) から \( y \) 方向に \( -2 \) だけ
進んだ点なので,\( (-2,-1) \) になります。
(3) 直線 \( l \) の方程式を求めなさい。
【解説】
右の図において,
直線 \( m \) は \( ∠PAF \) の二等分線なので,○ \( = \) ○
\( m⊥l \) なので,
○ \( + \) ✕ \( =90° \) ,○ \( + \) ✕ \( =90° \)
となり,✕ \( = \) ✕ になっています。
また,対頂角なので,✕ \( = \) ✕ でもあり,
✕ \( = \) ✕ になっています。
(2) で求めた点 \( (4,-1) \) を \( H \) とすると,
\( △AFH \) は \( AF=AH \) の二等辺三角形になっています。
また,直線 \( l \) は \( ∠FAH \) の二等分線であることから,線分 \( FH \) の中点を通ります。
線分 \( FH \) の中点を \( J \) とすると,
\( F(0,1),H(4,-1) \) より,点 \( J \) の座標は,
\( \left( \dfrac{0+4}{2},\dfrac{1+(-1)}{2} \right)=(2,0) \)
直線 \( l \) は,2点 \( A(4,4),J(2,0) \) を通るので,
傾き \( =\dfrac{4-0}{4-2}=2 \)
直線 \( l \) の式を \( y=2x+b \) とし,
\( x=2,y=0 \) を代入すると,
\( 0=2 \times 2+b \)
\( b=-4 \)
よって,直線 \( l \) の式は \( y=2x-4 \)
大問5
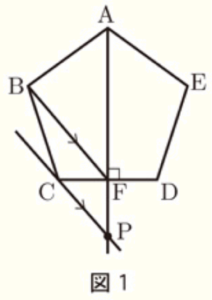
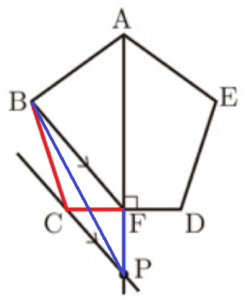
太郎さんは,正五角柱の形をしたケーキを4等分したいと考えています。<太郎さんの考え> を読み,(1)〜(3) に答えなさい。
<太郎さんの考え>
図1の正五角形 \( ABCDE \) は,ケーキを真上から見たときの模式図です。
ケーキを4等分するために,正五角形 \( ABCDE \) の面積を4等分する線分を考えます。
はじめに,点 \( A \) から辺 \( CD \) に垂線 \( AF \) をひくと,線分 \( AF \) は正五角形 \( ABCDE \) の面積を2等分します。
次に,点 \( B \) を通り,四角形 \( ABCF \) の面積を2等分する直線を考えます。点 \( C \) を通り,直線 \( BF \) に平行な直線と,直線 \( AF \) との交点を \( P \) とします。 このとき,\( △BCF \) の面積と (あ) の面積が等しいから,四角形 \( ABCF \) の面積は (い) の面積と等しくなります。
したがって, (う) を点 \( Q \) とすると,線分 \( BQ \) は四角形 \( ABCF \) の面積を2等分します。
同じように考えて,線分 \( EQ \) は四角形 \( AEDF \) の面積を2等分します。
以上のことから,線分 \( AF \),線分 \( BQ \),線分 \( EQ \) により,正五角形 \( ABCDE \) の面積は4等分されます。
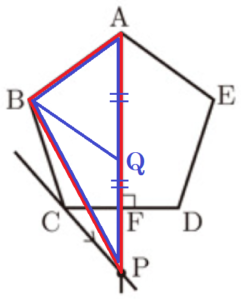
(1) (あ) , (い) に当てはまるものとして最も適当なのは,ア~カ のうちではどれですか。それぞれ一つ答えなさい。
ア \( △CPF \) イ \( △BPF \) ウ \( △BCP\)
エ \( △ACP \) オ \( △ABP \) カ 四角形 \( BCPF \)
【解説】
(あ)
線分 \( BF \) を固定して考えると,\( BF//CP \) より,等積変形の考え方から,\( △BCF \) と \( △BPF \) の面積は等しくなります。
(い)
四角形 \( ABCF \) の面積を \( △ABF+△BCF \) と考えると,\( △BCF=△BPF \) より,
\( △ABF+△BPF=△ABP \)
(2) (う) に当てはまるものとして最も適当なのは,ア~エ のうちではどれですか。一つ答えなさい。
ア 直線 \( BE \) と直線 \( AF \) との交点 イ 線分 \( AF \) の中点
ウ 線分 \( AP \) の中点 エ 直線 \( BD \) と直線 \( AF \) との交点
【解説】
(1) より,四角形 \( ABCF=△ABP \) なので,
点 \( Q \) が線分 \( AP \) の中点であるとき,
\( △BAQ \) と \( △BPQ \) は底辺の長さが等しく,
高さが共通な三角形になるので,面積が等しくなります。
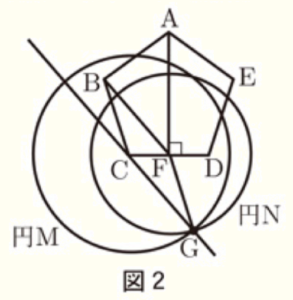
(3) 太郎さんは,下線部について,点 \( C \) を通り,直線 \( BF \) に平行な直線を<作図の手順>に従って作図し,作図した直線と直線 \( BF \) は平行であることを次のように説明しました。①,➁ に答えなさい。
<作図の手順>
手順1) 点 \( C \) を中心として,線分 \( BF \) の長さと等しい半径の円 \( M \) をかく。
手順2) 点 \( F \) を中心として,線分 \( BC \) の長さと等しい半径の円 \( N \) をかく。
手順3) 図2のように,2つの円の交点の1つを \( G \) とし,直線 \( CG \) をひく。
<作図した直線と直線 \( BF \) は平行であることの説明>
図2において,
\( △BCF ≡ △GFC \)
となり,
対応する角は等しいから,
\( ∠BFC=∠GCF \)
よって, (え) が等しいので,
\( BF//CG \)
となります。
① \( △BCF≡△GFC \) を証明しなさい。
【解答】
\( △BCF \) と \( △GFC \) において,
\( CF \) は共通 ・・・ ➀
仮定より,
\( BF=GC \) ・・・ ➁
\( BC=GF \) ・・・ ③
➀➁➂より,3組の辺の長さがそれぞれ等しいので,
\( △BCF≡△GFC \)
➁ (え) に当てはまるものとして最も適当なのは,ア~エ のうちではどれですか。 一つ答えなさい。
ア 対頂角 イ 同位角 ウ 錯角 エ 円周角