大問1
(1) \( x,y \) についての連立方程式 A,B がある。連立方程式 A,B の解が同じであるとき,\( a,b \) の値を求めなさい。
A \( \left\{ \begin{array}{}
-x-5y=7 \\
ax+by =9 \\
\end{array} \right. \) B \( \left\{ \begin{array}{}
2bx+ay=8 \\
3x+2y=5 \\
\end{array} \right. \)
【解説】
A,
B の解が同じということは,4つの方程式のどれを組み合わせても成り立つので,
\( \left\{ \begin{array}{}
-x-5y=7 \\
3x+2y=5 \\
\end{array} \right. \)
これを解くと,\( x=3,y=-2 \)
これを残りの2式に代入し,連立方程式にすると,
\( \left\{ \begin{array}{}
3a-2b=9 \\
6b-2a=8 \\
\end{array} \right. \)
これを解くと,\( a=5,b=3 \)
大問2
右の表は,あるクラスの生徒20人が受けた小テストの得点のデータを,度数分布表に整理したものである。
このデータを箱ひげ図で表したときに,度数分布表と矛盾するものを,次の ア~エ のうちからすべて選び,符号で答えなさい。
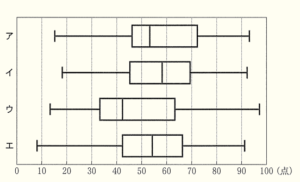
【解説】
度数分布表から,最小値,第一四分位数,中央値,第三四分位数,最大値がどの階級に含まれるかを確認すると,
最小値 ・・・ 10点以上20点未満
第一四分位数 ・・・ 40点以上50点未満
中央値 ・・・ 50点以上60点未満
第三四分位数 ・・・ 60点以上70点未満 または 70点以上80点未満
最大値 ・・・ 90点以上100点未満
なので,矛盾しているのは
ウ と
エ
ウ ・・・ 第一四分位数と中央値が合わない,エ ・・・ 最小値が合わない
大問3
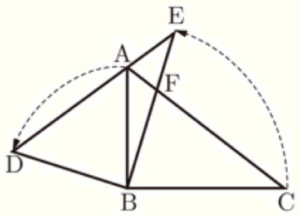
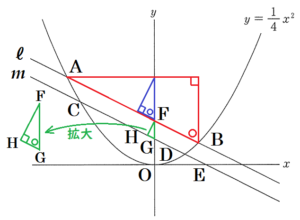
右の図の \( △ABC \) は,\( AB=3 \; cm, BC=4 \; cm \),
\( ∠ABC=90° \) の直角三角形である。\( △DBE \) は,\( △ABC \) を,点 \( B \) を中心として, 矢印の方向に回転させたものであり,\( △DBE \) の辺 \( DE \) 上に,\( △ABC \) の頂点 \( A \) がある。 また,辺 \( CA \) と辺 \( BE \) の交点を \( F \) とする。
このとき,次の ①,② の問いに答えなさい。
① 線分 \( AE \) の長さを求めなさい。
【解答】
\( \dfrac{7}{5} \; cm \)
【解説】
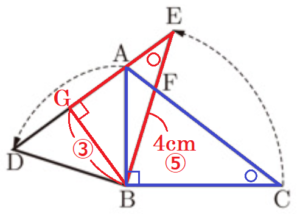
点 \( B \) から線分 \( DE \) に垂線をひき,交点を 点 \( G \) とすると,\( △ABC \) ∽ \( △BGA \) なので,
\( AB:AC=BG:BE \)
\( 3:5=BG:4 \)
\( BG=\dfrac{12}{5} \; (cm) \)
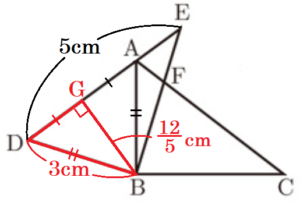
\( △BDG \) において,三平方の定理より,
\( DG^2=BD^2-BG^2 \)
\( =9-\dfrac{144}{25}=\dfrac{81}{25} \)
\( DG=\dfrac{9}{5} \; (cm) \)
\( DE=5 \; cm,DG=AG \) より,
\( AE=DE-2DG \)
\( =5-2 \times \dfrac{9}{5} \)
\( =\dfrac{7}{5} \; (cm) \)
② \( △ABF \) の面積を求めなさい。
【解答】
\( \dfrac{14}{13} \; cm^2 \)
【解説】
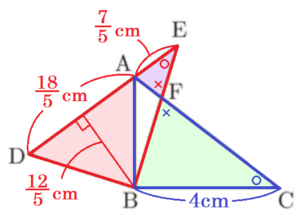
\( △ABD+△AEF+△ABF=△DBE \),
\( △BCF+△ABF=△ABC,△DBE=△ABC \) なので,
\( △ABD+△AEF+△ABF=△BCF+△ABF \)
\( △ABD+△AEF=△BCF \)
となっています。
また,
\( ∠AEF=∠BCF,∠AFE=∠BFC \) より,
\( △AEF \) ∽ \( △BCF \) であり,
相似比は,
\( AE:BC=\dfrac{7}{5}:4=7:20 \)
となっています。
ここから,\( △AEF \) と \( △BCF \) の面積比は,
\( 7^2:20^2=49:400 \)
となるので,\( △AEF \) の面積を \( 49S \) とすると,
\( △BCF \) の面積は \( 400S \) と表すことができます。
\( △ABD+△AEF=△BCF \) より,
\( \left( \dfrac{18}{5} \times \dfrac{12}{5} \times \dfrac{1}{2} \right)+49S=400S \)
\( 351S=\dfrac{18 \times 6}{25} \)
\( S=\dfrac{4}{13 \times 25} \)
\( △BCF+△ABF=△ABC \) より,
\( 400S+△ABF=3 \times 4 \times \dfrac{1}{2} \)
\( 400 \times \dfrac{4}{13 \times 25}+△ABF=6 \)
\( \dfrac{64}{13}+△ABF=6 \)
\( △ABF=\dfrac{14}{13} \; (cm^2) \)
大問4
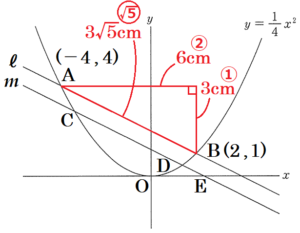
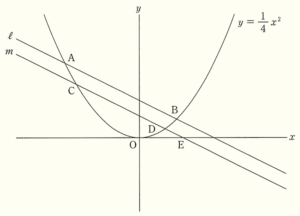
右の図のように,関数 \( y=\dfrac{1}{4}x^2 \) のグラフと,傾きが \( -\dfrac{1}{2} \) の2つの平行な直線 \( l,m \) がある。
関数 \( y=\dfrac{1}{4}x^2 \) のグラフと直線 \( l \) の交点を \( A,B \) とし,関数 \( y=\dfrac{1}{4}x^2 \) のグラフと直線 \( m \) の交点を \( C,D \) とする。
2点 \( A,B \) の \( x \) 座標は,それぞれ \( -4,2 \) であり,点 \( C \) の \( x \) 座標は,\( -4 \) より大きく \( 0 \) より小さい。また,直線 \( m \) と \( x \) 軸との交点を \( E \) とする。
このとき,次の ①,② の問いに答えなさい。
ただし, 原点 \( O \) から点 \( (1,0) \) までの距離及び原点 \( O \) から点 \( (0,1) \) までの距離をそれぞれ \( 1 \; cm \) とする。
① \( △ADB \) の面積が \( \dfrac{3}{7} \; cm^2 \) のとき,直線 \( m \) の式を求めなさい。
【解答】
\( y=-\dfrac{1}{2}x+\dfrac{13}{7} \)
【解説】
【方針】
直線 \( l \) と \( y \) 軸の交点を点 \( F \),
直線 \( m \) と \( y \) 軸の交点を点 \( G \) とし,
さらに,点 \( F \) から直線 \( m \) に垂線をひき,
交点を点 \( H \) とします。
赤の三角形と緑の三角形は相似であり,
線分 \( FH \) は \( △ADB \) の高さと等しいので,
\( △ADB \) の高さを求めると,
辺の比を用いて \( FG \) を求めることができます。
ここから,\( FG \) の長さを使って,点 \( G \) の \( y \) 座標を求めることで,直線 \( m \) の式を求めることができます。
【解答】
点 \( A \) は,\( y=\dfrac{1}{4}x^2 \) 上の点で,\( x \) 座標は \( -4 \) なので,
\( y=\dfrac{1}{4} \times (-4)^2=4 \)
点 \( B \) は,\( y=\dfrac{1}{4}x^2 \) 上の点で,\( x \) 座標は \( 2 \) なので,
\( y=\dfrac{1}{4} \times 2^2=1 \)
よって,
\( AB^2=6^2+3^2=45 \)
\( AB=3\sqrt{5} \; (cm) \)
\( △ADB \) の高さを \( h \) とすると,
\( △ADB=AB \times h \times \dfrac{1}{2} \)
\( \dfrac{3}{7}=3\sqrt{5} \times h \times \dfrac{1}{2} \)
\( h=\dfrac{2}{7\sqrt{5}} \; (cm) \)
右の図において,
\( FH:FG=2:\sqrt{5} \)
\( \dfrac{2}{7\sqrt{5}}:FG=2:\sqrt{5} \)
\( FG=\dfrac{1}{7} \; (cm) \)
直線 \( l \) の式を \( y=-\dfrac{1}{2}x+b \) とし,
\( x=2,y=1 \) を代入すると,
\( 1=-\dfrac{1}{2} \times 2+b \)
\( b=2 \)
なので,直線 \( l \) の式は, \( y=-\dfrac{1}{2}x+2 \)
ここから,点 \( F \) の座標は,\( F(0,2) \)
よって,点 \( G \) の座標は,\( G \left( 0,2-\dfrac{1}{7}=\dfrac{13}{7} \right) \) となるので,
直線 \( m \) の式は, \( y=-\dfrac{1}{2}x+\dfrac{13}{7} \)
② 四角形 \( ACEB \) が平行四辺形になるとき, 直線 \( m \) の切片を求めなさい。
平行四辺形の向かい合う辺の長さは等しいので,
右の図で赤と青の三角形は合同になっています。
ここで,点 \( C \) は \( y=\dfrac{1}{4}x^2 \) 上の点なので,
\( x \) 座標を \( t \) とすると,
\( y \) 座標は,\( \dfrac{1}{4}t^2 \) と表すことができます。
点 \( C \) の \( y \) 座標は \( 3 \) なので,
\( \dfrac{1}{4}t^2=3 \)
\( t=-2\sqrt{3} \) ( \( t<0 \) より)
直線 \( m \) の式を \( y=-\dfrac{1}{2}x+b \) とし,
\( x=-2\sqrt{3},y=3 \) を代入すると,
\( 3=-\dfrac{1}{2} \times (-2\sqrt{3})+b \)
\( b=3-\sqrt{3} \)
よって,直線 \( m \) の切片は \( 3-\sqrt{3} \)