大問1
(1) \( -3^2 \times \{ 7-(-4)^2 \} \) を計算せよ。
【解説】
\( =-9 \times (7-16) \)
\( =-9 \times (-9) \)
\( =81 \)
(2) \( \dfrac{3x-2y}{6}-\dfrac{4x-y}{8} \) を計算せよ。
【解答】
\( -\dfrac{5}{24}y \)
【解説】
\( =\dfrac{4(3x-2y)-3(4x-y)}{24} \)
\( =\dfrac{12x-8y-12x+3y}{24} \)
\( =-\dfrac{5}{24}y \)
(3) \( 3\sqrt{50}-\sqrt{2}-\sqrt{54} \div \sqrt{3} \) を計算せよ。
【解説】
\( =3 \times 5\sqrt{2}-\sqrt{2}-3\sqrt{6} \div \sqrt{3} \)
\( =15\sqrt{2}-\sqrt{2}-3\sqrt{2} \)
\( =11\sqrt{2} \)
(4) 次の連立方程式を解け。
\( \left\{ \begin{array}{}
2x-3y=5 \\
3x-(4x-6y)=-1 \\
\end{array} \right. \)
【解答】
\( x=3,y=\dfrac{1}{3} \)
【解説】
\( \left\{ \begin{array}{}
2x-3y=5 \;\; ・・・ \;\; ➀ \\
3x-(4x-6y)=-1 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁より,
\( -x+6y=-1 \) ・・・ ➁’
➀\( \times 2 \)\( + \) ➁’
\( 3x=9 \)
\( x=3 \)
➁’に代入すると,
\( -3+6y=-1 \)
\( 6y=2 \)
\( y=\dfrac{1}{3} \)
(5) 関数 \( y=-2x^2 \) について,\( x \) の値が \( a \) から \( a+2 \) まで増加するときの変化の割合が \( -40 \) である。このとき,\( a \) の値を求めよ。
【解説】
\( y=-2x^2 \) において,
\( x=a \) のとき,\( y=-2a^2 \)
\( x=a+2 \) のとき,\( y=-2(a+2)^2 \)
なので,変化の割合を \( a \) を使って表すと,
\( \dfrac{\{-2(a+2)^2 \}-(-2a^2)}{(a+2)-a}=\dfrac{-2\{(a+2)^2-a^2 \}}{2} \)
\( =-4a-4 \)
よって,変化の割合の関係は,
\( -4a-4=-40 \)
\( -4a=-36 \)
\( a=9 \)
(6) \( (2x+y+5)(2x+y-5) \) を展開せよ。
【解答】
\( 4x^2+4xy+y^2-25 \)
【解説】
\( 2x+y=A \) とすると,
与式 \( =(A+5)(A-5) \)
\( =A^2-25 \)
\( =(2x+y)^2-25 \)
\( =4x^2+4xy+y^2-25 \)
(7) 2次方程式 \( 6x^2+2x-1=0 \) を解け。
【解答】
\( x=\dfrac{-1±\sqrt{7}}{6} \)
【解説】
この2次方程式を \( ax^2+bx+c=0 \) とすると,\( a=6,b=2,c=-1 \) なので,
解の公式より,
\( x=\dfrac{-2±\sqrt{2^2-4 \times 6 \times (-1)}}{2 \times 6} \)
\( =\dfrac{-2±\sqrt{28}}{12} \)
\( =\dfrac{-2±2\sqrt{7}}{12} \)
\( =\dfrac{-1±\sqrt{7}}{6} \)
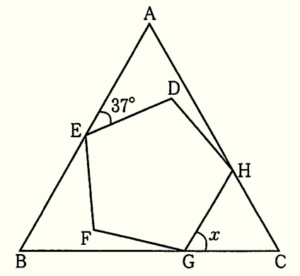
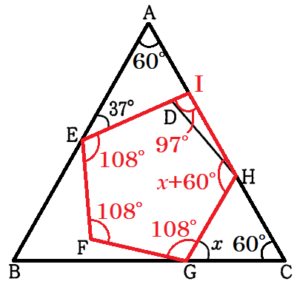
(8) 右の図のように,正三角形 \( ABC \) と正五角形 \( DEFGH \) があり,頂点 \( E \) は辺 \( AB \) 上に,頂点 \( G \) は辺 \( BC \) 上に,頂点 \( H \) は辺 \( CA \) 上にある。このとき,\( ∠x \) の大きさを求めよ。
【解説】
線分 \(ED\) を延長したときの線分 \( AC \) との交点を点 \( I \) とすると,
五角形 \( DEFGH \) において,
\( △AEI \) の外角なので,\( ∠EIH=37°+60°=97° \)
\( △CGH \) の外角なので,\( ∠GHI=∠x+60° \)
正五角形の内角の和は \( 540° \) なので,
1つの角は \( \dfrac{540°}{5}=108° \) であり,
\( ∠E=∠F=∠G=108° \)
よって,
\( 108° \times 3+97°+(x+60°)=540° \)
\( x+481°=540° \)
\( x=59° \)
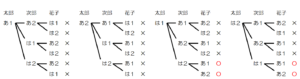
(9) あたりくじが2本,はずれくじが2本の合計4本のくじが入った箱がある。この箱から,太郎さん,次郎さん,花子さんが,この順に1本ずつくじをひく。このとき,花子さんだけがあたりくじをひく確率を求めよ。ただし,ひいたくじは箱にもどさず,どのくじがひかれることも同様に確からしいものとする。
【解説】
2本のあたりくじに「あ1,あ2」,2本のはずれくじに「は1,は2」と名前をつけ,
3人がひいたくじの組み合わせを樹形図に書いてみると,
花子さんだけがあたりくじをひく組み合わせは4通り,すべての組み合わせは24通りなので,
求める確率は,\( \dfrac{4}{24}=\dfrac{1}{6} \)
大問2
ある中学校のボランティア部に所属する生徒9人と,先生1人の合計10人がごみ拾いのボランティア活動に参加した。次の資料は,生徒9人がそれぞれ拾ったペットボトルの本数を示したものである。資料中の \( a,b \) は \( 0<a<b \) であり,生徒9人がそれぞれ拾ったペットボトルの本数はすべて異なっていた。また,生徒9人がそれぞれ拾ったペットボトルの本数の平均値はちょうど8本であった。

このとき,次の問い(1)・(2)に答えよ。
(1) \( a,b \) の値をそれぞれ求めよ。
【解説】
平均値は,「すべてのデータの合計値 \( \div \) データの個数」で求められるので,
「すべてのデータの合計値 \( = \) 平均値 \( \times \) データの個数」で求めることができます。
拾ったペットボトルの本数の平均値は8本なので,
生徒9人が拾ったペットボトルの本数の合計は,\( 8 \times 9=72 \)(本)であり,
\( 3+9+15+6+11+8+4+a+b=72 \)
\( a+b=16 \)
\( a+b=16 \) を満たす \( (a,b) \; (0<a<b) \) の組み合わせは,
\( (a,b)=(1,\fbox{15}),(2,14),(\fbox{3},13),(\fbox{4},12),(5,\fbox{11}),(\fbox{6},10),(7,\fbox{9}) \)
であり,
\( 3,9,15,6,11,8,4 \) をどれも使わない組み合わせは,\( a=2,b=14 \)
(2) 資料に,先生が拾ったペットボトルの本数を追加すると,生徒と先生の合計10人がそれぞれ拾ったペットボトルの本数の四分位範囲はちょうど9本であった。このとき,先生が拾ったペットボトルの本数を求めよ。
【解説】
四分位範囲は,「第三四分位数 \( – \) 第一四分位数」で求められます。
先生を含めて合計10人のデータを集めたので,
第一四分位数は少ない方から3番目の人の本数,
第三四分位数は少ない方から8番目(多い方から3番目)の人の本数
になります。
生徒9人がそれぞれ拾ったペットボトルの本数を少ない順に並べると,
\( 2,3,4,6,8,9,11,14,15 \)
となるので。
少ない方から3番目の人の本数が \( 4 \) 本,多い方から3番目人の本数が \( 11 \) 本であると仮定して
四分位範囲を求めると,\( 11-4=7 \)(本)となり,あてはまりません。
ここから,第一四分位数の \( 4 \) 本,第三四分位数の \( 11 \) 本のどちらかは間違っているとわかります。
ここで,第一四分位数の \( 4 \) 本が正しいと仮定すると,
第三四分位数は \( 4+9=13 \)(本)になるので,
先生が拾ったペットボトルの本数を \( 13 \) 本として,拾った本数の順番に書き加えると,
\( 2,3,4,6,8,9,11,\fbox{13},14,15 \)
となり,多い方から3番目になっているのであてはまります。
次に,第三四分位数の \( 11 \) 本が正しいと仮定すると,
第一四分位数は \( 11-9=2 \)(本)になります。
先生が拾ったペットボトルの本数を \( 2 \) 本として,拾った本数の順番に書き加えると,
\( 2,\fbox{2},3,4,6,8,9,11,14,15 \)
先生が拾ったペットボトルの本数を \( 1 \) 本として,拾った本数の順番に書き加えると,
\( 1,\fbox{2},3,4,6,8,9,11,14,15 \)
となり,どちらにしても少ない方から3番目にならないのであてはまりません。
よって,先生が拾ったペットボトルの本数は \( 13 \) 本であったとわかります。
大問3
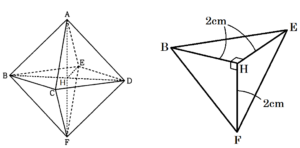
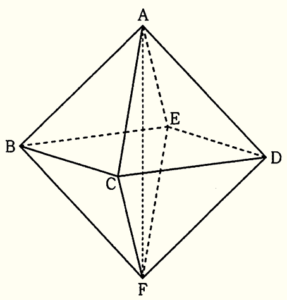
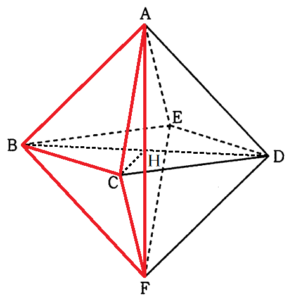
右の図のように,正八面体 \( ABCDEF \) がある。また,\( AF=4 \; cm \) である。
このとき,次の問い(1)~(3)に答えよ。
(1) この正八面体の1辺の長さを求めよ。
【解答】
\( 2\sqrt{2} \; cm \)
【解説】
正八面体は,すべての辺の長さが等しく,
合同な四角すいを上下ひっくり返してくっつけた形になっているので,
線分 \( BD \) と \( CE \) の交点を点 \( H \) とすると,
\( AH=\dfrac{1}{2}AF=2 \; cm \)
になっています。
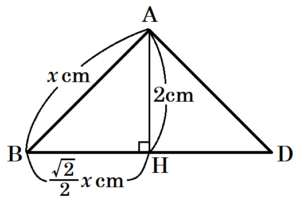
四角すい \( ABCDE \) だけに注目し,
1辺の長さを \( x \; cm \) とすると,
四角形 \( BCDE \) は正方形なので,
\( BD=\sqrt{2}x \; cm,BH=\dfrac{\sqrt{2}}{2}x \; cm \)
\( △ABH \) において,三平方の定理より,
\( AB^2=AH^2+BH^2 \)
\( x^2=2^2+\left( \dfrac{\sqrt{2}}{2}x \right)^2 \)
\( x^2=4+\dfrac{1}{2}x^2 \)
\( \dfrac{1}{2}x^2=4 \)
\( x^2=8 \)
\( x=2\sqrt{2} \; (cm) \) (\( x>0 \) より)
(2) 線分 \( BD \) の中点を \( H \) とするとき,三角錐 \( HBFE \) の体積を求めよ。
【解答】
\( \dfrac{4}{3} \; cm^3 \)
【解説】
四角形 \( BCDE \) は正方形で,1辺の長さは \( 2\sqrt{2} \; cm \) なので,
\( BD=\sqrt{2} \times 2\sqrt{2}=4 \; (cm),BH=\dfrac{1}{2}BD=2 \; (cm) \)
正方形の対角線はそれぞれの中点で交わるので,\( EH=BH=2 \; cm \)
また,\( FH=\dfrac{1}{2}AF=2 \; (cm) \) なので,
三角すい \( HBFE \) の体積は,
\( \left( 2 \times 2 \times \dfrac{1}{2} \right) \times 2 \times \dfrac{1}{3}=\dfrac{4}{3} \; (cm^3) \)
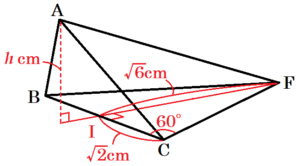
(3) 点 \( A \) と平面 \( BFC \) との距離を求めよ。
【解答】
\( \dfrac{4\sqrt{3}}{3} \; cm \)
【解説】
三角すい \( ABCF \) に注目すると,
三角すい \( ABCH \) と \( FBCH \) をくっつけた形になっています。
\( △BEH≡△BCH,AH=FH \) より,
三角すい \( HBFE \),三角すい \( ABCH \),三角すい \( FBCH \) は
体積が等しくなるので,(2)より,体積は \( \dfrac{4}{3} \; cm^3 \)
ここから,三角すい \( ABCF \) の体積は,\( 2 \times \dfrac{4}{3}=\dfrac{8}{3} \; (cm^3) \)
\( △BCF \) を三角すい \( ABCF \) の底面と考えると,
点 \( A \) から平面 \( BFC \)におろした垂線の長さ
つまり,三角すい \( ABCF \) の高さが
点 \( A \) と平面 \( BFC \) との距離になります。
\( △BCF \) は正三角形なので,
点 \( F \) から線分 \( BC \) に垂線をひき,
交点を 点 \( I \) とすると,
点 \( I \) は線分 \( BC \) の中点なので,
\( FI=\sqrt{3}CI=\sqrt{6} \; (cm) \)
よって,\( △BCF \) の面積は,
\( △BCF=2\sqrt{2} \times \sqrt{6} \times \dfrac{1}{2} \)
\( =2\sqrt{3} \; (cm^2) \)
以上より,三角すい \( ABCF \) の高さを \( h \; cm \) すると,体積を表す関係式は,
三角すい \( ABCF=2\sqrt{3} \times h \times \dfrac{1}{3} \)
\( \dfrac{8}{3}=2\sqrt{3} \times h \times \dfrac{1}{3} \)
\( 8=2\sqrt{3}h \)
\( h=\dfrac{4\sqrt{3}}{3} \; (cm) \)
大問4
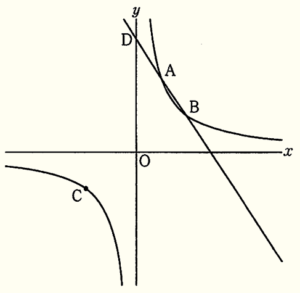
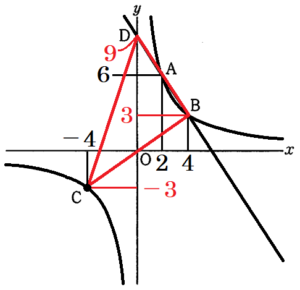
右の図のように,関数 \( y=\dfrac{a}{x} \) のグラフ上に3点 \( A,B,C \) があり,点 \( A \) の座標は \( (2,6) \),点 \( B \) の \( x \) 座標は \( 4 \),点 \( C \) の \( x \) 座標は \( -4 \) である。また,2点 \( A,B \) を通る直線と \( y \) 軸との交点を \( D \) とする。
このとき,次の問い(1)・(2)に答えよ。
(1) \( a \) の値を求めよ。また,\( △BDC \) の面積を求めよ。
【解答】
\( a \) の値 ・・・ \( a=12 \)
\( △BDC \) の面積 ・・・ \( 36 \)
【解説】
点 \( A \) は \( y=\dfrac{a}{x} \) 上の点なので,
\( x=2,y=6 \) を代入すると,
\( 6=\dfrac{a}{2} \)
\( a=12 \)
点 \( B,C \) は,どちらも \( y=\dfrac{12}{x} \) 上の点で,
\( x \) 座標はそれぞれ \( 4,-4 \) なので,
\( y \) 座標はそれぞれ \( 3,-3 \) になります。
よって,点 \( B,C \) の座標は,\( B(4,3),C(-4,-3) \)
点 \( B,C \) は,原点 \( O \) について対称な点なので,辺 \( BC \) は原点を通ります。
また,直線 \( AB \) は \( A(2,6),B(4,3) \) を通るので,
傾き \( =\dfrac{3-6}{4-2}=-\dfrac{3}{2} \)
直線 \( AB \) の式を \( y=-\dfrac{3}{2}x+b \) とし,\( x=2,y=6 \) を代入すると,
\( 6=-\dfrac{3}{2} \times 2+b \)
\( b=9 \)
よって,点 \( D \) の座標は,\( D(0,9) \)
以上より,
\( △BDC=△BOD+△COD \)
\( =9 \times 4 \times \dfrac{1}{2}+9 \times 4 \times \dfrac{1}{2} \)
\( =36 \)
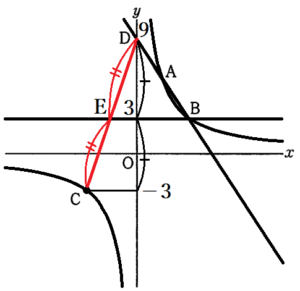
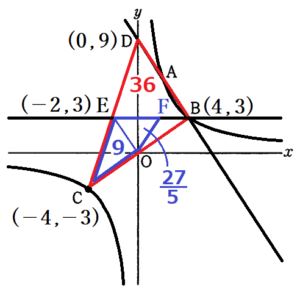
(2) 点 \( B \) を通り \( x \) 軸に平行な直線と2点 \( C,D \) を通る直線との交点を \( E \) とする。また,線分 \( BE \) 上に点 \( F \) を,四角形 \( COFE \) の面積が \( △BDC \) の面積の \( \dfrac{2}{5} \) 倍となるようにとる。このとき,点 \( F \) の \( x \) 座標を求めよ。
【解説】
点 \( E \) の \( y \) 座標は点 \( B \) と等しく,\( 3 \) になります。
また,線分 \( CD \) 上の点でもあり,
点 \( C,D \) の \( y \) 座標は,それぞれ \( -3,9 \) なので,
線分 \( CD \) の中点の \( y \) 座標は
\( \dfrac{9+(-3)}{2}=3 \)
であり,点 \( E \) が線分 \( CD \) の中点になるとわかります。
ここで,線分 \( OE \) をひくと,
四角形 \( COFE \) を \( △OEC \) と \( △OFE \) に分けることができます。
点 \( O \) も線分 \( BC \) の中点なので,
\( △OEC \) ∽ \( △BDC \) で,相似比は \( 1:2 \)
相似な三角形の面積比は相似比の2乗の比なので,
\( △OEC:△BDC=1^2:2^2=1:4 \)
(1)より,\( △BDC \) の面積は \( 36 \) なので,
\( △OEC \) の面積は \( 9 \) になります。
四角形 \( COFE \) の面積は,
\( △BDC \) の面積の \( \dfrac{2}{5} \) 倍なので,
\( 36 \times \dfrac{2}{5}=\dfrac{72}{5} \)
ここから,\( △OFE \) の面積は
\( \dfrac{72}{5}-9=\dfrac{27}{5} \)
線分 \( EF \) の長さを \( t \) とすると,
\( t \times 3 \times \dfrac{1}{2}=\dfrac{27}{5} \)
\( t=\dfrac{18}{5} \)
点 \( E \) は線分 \( CD \) の中点なので,\( x \) 座標の値は \( -2 \) であり,
点 \( F \) の \( x \) 座標は,
\( -2+\dfrac{18}{5}=\dfrac{8}{5} \)
大問5
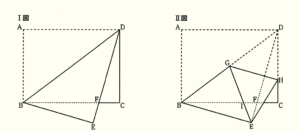
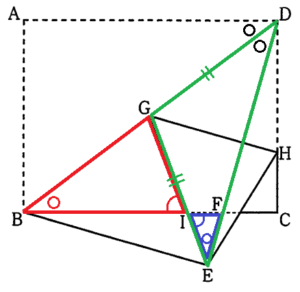
下のⅠ図のように,\( AB=6 \; cm,AD=8 \; cm \) の長方形 \( ABCD \) を,対角線 \( BD \) を折り目として折り返し,点 \( A \) が移った点を \( E \),辺 \( BC \) と線分 \( DE \) との交点を \( F \) とする。さらに,右のⅡ図のように,点 \( D \) が点 \( E \) と重なるように折り,折り目となる直線と線分 \( BD \),辺 \( CD \) との交点をそれぞれ \( G,H \) とする。また,辺 \( BC \) と線分 \( EG \) との交点を \( I \) とする。
このとき,次の問い(1)~(3)に答えよ。
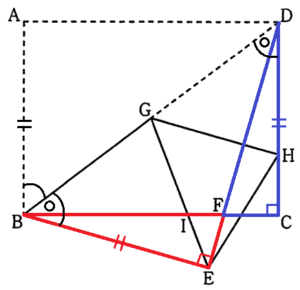
(1) \( △IGB \) ∽ \( △IFE \) であることを証明せよ。
【解答】
\( △IGB \) と \( △IFE \) において,
対頂角は等しいので,
\( ∠BIG=∠EIF \) ・・・ ➀
長方形の向かい合う辺は平行なので \( AD//BC \)
錯角は等しいので,
\( ∠BDA=∠GBI \) ・・・ ➁
折り返す前後の図形は合同で,\( △BDA≡△BDE \)
対応する角は等しいので,
\( ∠BDA=∠BDE \) ・・・ ➂
折り返す前後の図形は合同で,\( △GDH≡△GEH \)
対応する辺は等しいので,\( GD=GE \)
\( △GDE \) は二等辺三角形であり,
底角は等しいので,
\( ∠FEI=∠GDE \) ・・・ ➃
➁➂➃より,
\( ∠GBI=∠FEI \) ・・・ ➄
①➄より,2組の角がそれぞれ等しいので,
\( △IGB \) ∽ \( △IFE \)
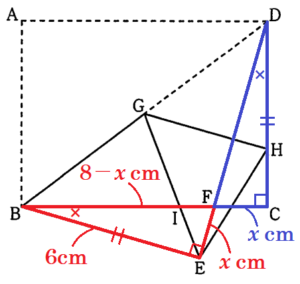
(2) 線分 \( EF \) の長さを求めよ。
【解答】
\( \dfrac{7}{4} \; cm \)
【解説】
\( ∠BEF=∠DCF,∠EBF=∠CDF,EB=CD \) より,\( △EBF≡△CDF \)
\( EF=x \; cm \) とすると,
\( BC=AD=8 \; cm,CF=EF=x \; cm \) より,
\( BF=8-x \; cm \)
\( EB=AB=6 \; cm \) なので,三平方の定理より,
\( BF^2=EB^2+EF^2 \)
\( (8-x)^2=6^2+x^2 \)
\( 16x=28 \)
\( x=\dfrac{7}{4} \; (cm) \)
△EBF≡△CDFの証明
\( △EBF \) と \( △CDF \) において,
長方形のすべての角は \( 90° \) なので,
\( ∠BEF=∠DCF \) ・・・ ➀
長方形の向かい合う辺は平行なので,\( AB//CD \)
錯角は等しいので,\( ∠ABD=∠CDB \)
折り返す前後の図形は合同なので,\( ∠ABD=∠EBD \)
よって,\( ∠EBD=∠CDB \)
(1)より,\( ∠GBI=∠BDE \) なので,
\( ∠EBF=∠EBD-∠GBI \)
\( ∠CDF=∠CDB-∠BDE \)
より,
\( ∠EBF=∠CDF \) ・・・ ➁
長方形の向かい合う辺は等しいので,\( AB=CD \)
折り返す前後の図形は合同なので,\( AB=EB \)
よって,\( EB=CD \) ・・・ ➂
①➁➂より,1組の辺とその両端の角がそれぞれ等しいので,\( △EBF≡△CDF \)
(3) 線分 \( BI \) の長さを求めよ。
【解答】
\( \dfrac{200}{39} \; cm \)
【解説】
\( AB=6 \; cm,AD=8 \; cm \) より,
\( BD^2=6^2+8^2=100 \)
\( BD=10 \; (cm) \) (\( BD>0 \) より)
点 \( G \) は線分 \( BD \) の中点なので,\( BG=5 \; cm \)
(1)より,\( △IGB \) ∽ \( △IFE \) であり,
相似比は,\( BG:EF=5:\dfrac{7}{4}=20:7 \)
対応する辺の比は等しいので,
\( BI=x \; cm \) とすると,\( EI=\dfrac{7}{20}x \; cm \)
\( GE=DG=5 \; cm \) なので,\( GI=5-\dfrac{7}{20}x \; cm \)
対応する辺の比は等しいので,
\( FI=\dfrac{7}{20} \left( 5-\dfrac{7}{20}x \right) \; cm \)
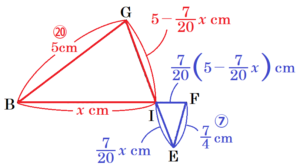
↑ \( △IGB \) と \( △IFE \) のみ抜粋しています。
\( BC=8 \; cm,CF=EF=\dfrac{7}{4} \; cm \) より,\( BF=\dfrac{25}{4} \; cm \) なので,
\( BF=BI+FI \)
\( \dfrac{25}{4}=x+\dfrac{7}{20} \left( 5-\dfrac{7}{20}x \right) \)
\( \dfrac{25}{4}=x+\dfrac{7}{4}-\dfrac{49}{400}x \)
\( \dfrac{351}{400}x=\dfrac{18}{4} \)
\( x=\dfrac{200}{39} \; (cm) \)
BI=20x とおくとちょっとだけ計算がラクになる
\( BI=20x \; cm \) とすると,\( EI=7x \; cm \)
\( GE=DG=5 \; cm \) なので,\( GI=5-7x \; cm \)
対応する辺の比は等しいので,\( FI=\dfrac{7}{20} (5-7x) \; cm \)
\( BF=BI+FI \)
\( \dfrac{25}{4}=20x+\dfrac{7}{20} (5-7x) \)
\( 125=400x+7 (5-7x) \)
\( 351x=90 \)
\( x=\dfrac{10}{39} \)
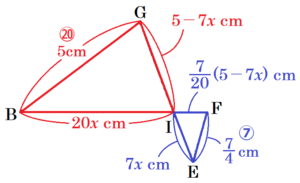
↑ \( △IGB \) と \( △IFE \) のみ抜粋しています。
よって,\( BI=20x=20 \times \dfrac{10}{39}=\dfrac{200}{39} \; (cm) \)
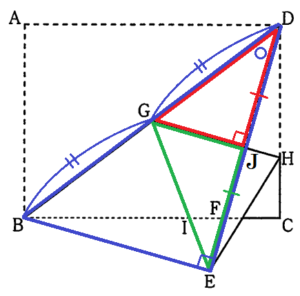
点Gが辺BCの中点であることの証明
折り返す前後の点を結ぶ線分は
折り目となる線分と中点で垂直に交わるので,
線分 \( DE \) と線分 \( GH \) の交点を点 \( J \) とすると,
\( DJ=EJ,DE⊥GH \)
となります。
\( △DGJ \) と \( △DBE \) において,
\( ∠DJG=∠DEB,∠D \) は共通
より,
\( △DGJ \) ∽ \( △DBE \)
対応する辺の比は等しいので,
\( DG:DB=DJ:DE=1:2 \)
よって,点 \( G \) は線分 \( BD \) の中点になります。
大問6
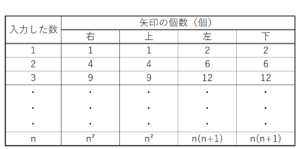
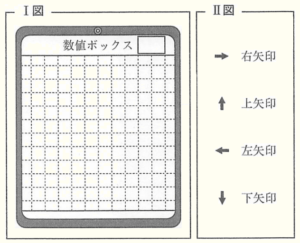
プログラミング教室で,規則的に図形を表示するプログラムをつくった。右のⅠ図は,タブレット端末でこのプログラムを実行すると,初めに表示される画面を表している。画面上の数値ボックスに自然数を入力すると,入力した数に応じて,右のⅡ図のような,右矢印,上矢印,左矢印,下矢印の4種類の矢印が規則的に表示される。 次のⅢ図は,数値ボックスに \( 1,2,3, \) ・・・ をそれぞれ入力したときの画面を表している。
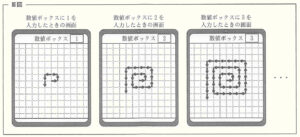
このとき,次の問い(1)~(3)に答えよ。ただし,数値ボックスにどのような自然数を入力しても,すべての矢印は表示されるものとする。
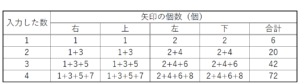
(1) 数値ボックスに \( 4 \) を入力したとき,表示される4種類の矢印の個数の合計を求めよ。
【解説】
数値ボックスに \( 4 \) を入力したとき,表示される矢印の個数は,
右矢印の個数 \( =1+3+5+7=16 \)(個)
上矢印の個数 \( =1+3+5+7=16 \)(個)
左矢印の個数 \( =2+4+6+8=20 \)(個)
下矢印の個数 \( =2+4+6+8=20 \)(個)
よって,4種類の矢印の個数の合計は,
\( 16+16+20+20=72 \)(個)
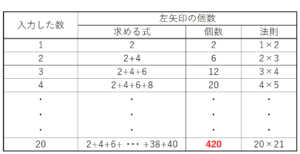
(2) 数値ボックスに \( 20 \) を入力したとき,表示される左矢印の個数を求めよ。
【解説】
入力した自然数を \( n \) とするとき,
表示される左矢印の個数は,\( n(n+1) \) と表すことができるので,
\( 20 \) を入力したときは,\( 20 \times 21=420 \)(個)
(3) 表示されている4種類の矢印のうち,上矢印,左矢印,下矢印の個数の合計と右矢印の個数の差が \( 6160 \) 個となるとき,数値ボックスに入力した自然数を求めよ。
【解説】
入力した自然数を \( n \) とするとき,表示される左矢印の個数は,
右矢印と上矢印がそれぞれ \( n^2 \) ,左矢印と下矢印がそれぞれ \( n(n+1) \) と表すことができるので,
上 \( + \) 左 \( + \) 下 \( – \) 右 \( =6160 \)
\( n^2+n(n+1)+n(n+1)-n^2=6160 \)
\( 2n(n+1)=6160 \)
\( n(n+1)=3080=55 \times 56 \)
\( n=55 \)











-アイキャッチ-120x68.jpg)
-アイキャッチ-120x68.jpg)