大問1
(1) \( -6^2+4 \div \left( -\dfrac{2}{3} \right) \) を計算せよ。
【解説】
\( =-36+4 \times \left( -\dfrac{3}{2} \right) \)
\( =-36-6 \)
\( =-42 \)
(2) \( 4ab^2 \div 6a^2b \times 3ab \) を計算せよ。
【解説】
\( =\dfrac{4ab^2 \times 3ab}{6a^2b} \)
\( =2b^2 \)
(3) \( \sqrt{48}-3\sqrt{2} \times \sqrt{24} \) を計算せよ。
【解説】
\( =4\sqrt{3}-3\sqrt{2} \times 2\sqrt{6} \)
\( =4\sqrt{3}-6\sqrt{12} \)
\( =4\sqrt{3}-12\sqrt{3} \)
\( =-8\sqrt{3} \)
(4) 次の連立方程式を解け。
\( \left\{ \begin{array}{}
4x+3y=-7 \\
3x+4y=-14 \\
\end{array} \right. \)
【解説】
\( \left\{ \begin{array}{}
4x+3y=-7 \;\; ・・・ \;\; ➀ \\
3x+4y=-14 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀\( \times 4- \)➁ \( \times 3 \)
\( 7x=14 \)
\( x=2 \)
➀ に代入すると,
\( 4 \times 2+3y=-7 \)
\( 3y=-15 \)
\( y=-5 \)
(5) \( x=\sqrt{5}+3,y=\sqrt{5}-3 \) のとき,\( xy^2-x^2y \) の値を求めよ。
【解説】
\( xy^2-x^2y=xy(y-x) \)
\( x=\sqrt{5}+3,y=\sqrt{5}-3 \) より,
\( xy=(\sqrt{5}+3)(\sqrt{5}-3)=5-9=-4 \)
\( y-x=(\sqrt{5}-3)-(\sqrt{5}+3)=-6 \)
なので,
\( xy(y-x)=-4 \times (-6)=24 \)
(6) 関数 \( y=\dfrac{16}{x} \) のグラフ上にあり,\( x \) 座標,\( y \) 座標がともに整数となる点の個数を求めよ。
【解説】
\( y=\dfrac{16}{x} \) より,\( xy=16 \) なので,
\( x,y \) は \( 16 \) の約数になります。
\( 16 \) の約数は \( 1,2,4,8,16 \) なので,
あてはまるのは,
\( (x,y)=(1,16),(2,8),(4,4),(8,2),(16,1) \)
さらに,\( x \) 座標,\( y \) 座標がともに整数となる点なので,負の数の組み合わせ
\( (x,y)=(-1,-16),(-2,-8),(-4,-4), \)
\( (-8,-2),(-16,-1) \) も含みます。
よって,あてはまる点の個数は,10個
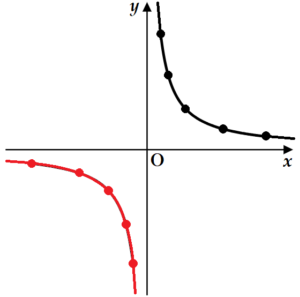 \( y=\dfrac{16}{x} \) は反比例を表しているので,
\( y=\dfrac{16}{x} \) は反比例を表しているので,
グラフの曲線は2本になります。
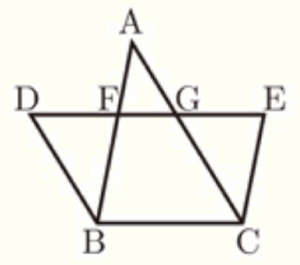
(7)右の図において,\( AB//EC,AC//DB,DE //BC \) である。また,線分 \( DE \) と線分 \( AB,AC \) との交点をそれぞれ \( F,G \) とすると,\( AF:FB=2:3 \) であった。\( BC=10 \; cm \) のとき,線分 \( DE \) の長さを求めよ。
【解説】
\( AB//EC,AC//DB,DE //BC \) より,
同位角,錯角は等しく,2組の角がそれぞれ等しいので,
\( △AFG,△ABC,△BFD,△CEG \) は
それぞれ相似になっています。
\( △AFG \) と \( △ABC \) の相似比は \( 2:5 \) なので,
\( FG=\dfrac{2}{5}BC=4 \; (cm) \)
\( △AFG \) と \( △BFD \) の相似比は \( 2:3 \) なので,
\( FD=\dfrac{3}{2}FG=6 \; (cm) \)
\( △AFG \) と \( △CEG \) の相似比は \( 2:3 \) なので,
\( EG=\dfrac{3}{2}FG=6 \; (cm) \)
よって,\( DE=FD+FG+EG=4+6+6=16 \; (cm) \)
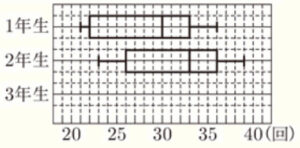
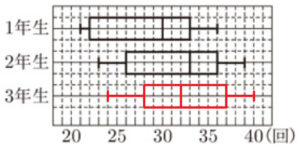
(8) 3学年がそれぞれ8クラスで編成された,ある中学校の体育の授業で,長なわ跳びを行った。右の図は,各クラスが連続で跳んだ回数の最高記録を, 学年ごとに箱ひげ図で表そうとしている途中のものであり,1年生と2年生の箱ひげ図はすでにかき終えている。また,右の資料は,3年生のクラスごとの最高記録をまとめたものである。図の1年生と2年生の箱ひげ図を参考にし,答案用紙の図に3年生の箱ひげ図をかき入れて,図を完成させよ。

【解説】
3年生のクラスごとの最高記録を回数の少ない方から順に並べ替えると,
\( 24,28,28,31,33,35,39,40 \)
全部で8クラスなので,
第一四分位数は少ない方から2番目と3番目の記録の平均値であり,\( \dfrac{28+28}{2}=28 \)(回)
中央値は少ない方から4番目と5番目の記録の平均値であり,\( \dfrac{31+33}{2}=32 \)(回)
第三四分位数は少ない方から6番目と7番目の記録の平均値であり,\( \dfrac{35+39}{2}=37 \)(回)
大問2
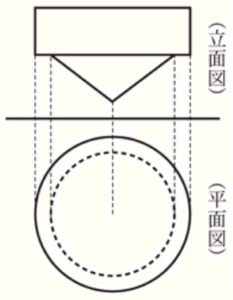
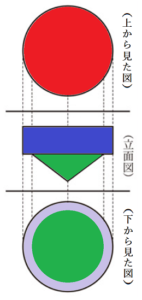
底面の半径が \( 5 \; cm \) の円柱と,底面の半径が \( 4 \; cm \) の円錐があり,いずれも高さは \( 3 \; cm \) である。この2つの立体の底面の中心を重ねてできた立体を \( X \) とすると,立体 \( X \) の投影図は右の図のように表される。
このとき,次の問い(1)・(2)に答えよ。
(1) 立体 \( X \) の体積を求めよ。
【解答】
\( 91\pi{} \; cm^3 \)
【解説】
円柱の体積 \( =\pi{} \times 5^2 \times 3=75\pi{} \; (cm^3) \)
円すいの体積 \( =\pi{} \times 4^2 \times 3 \times \dfrac{1}{3}=16\pi{} \; (cm^3) \)
なので,
立体 \( X \) の体積 \( =75\pi{}+16\pi{}=91\pi{} \; (cm^3) \)
(2) 立体 \( X \) の表面積を求めよ。
【解答】
\( 84\pi{} \; cm^2 \)
【解説】
立体 \( X \) の面は右の図で色分けしたように
4つの面に分かれています。
【赤の面】
\( \pi{} \times 5^2=25\pi{} \; (cm^2) \)
【青の面】
\( 3 \times (2\pi{} \times 5)=30\pi{} \; (cm^2) \)
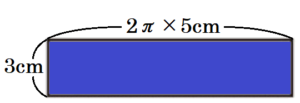
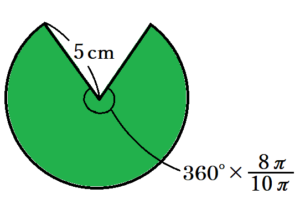
【緑の面】
円すいの母線の長さは \( 5 \; cm \),
底面の円周の長さは \( 2\pi{} \times 4=8\pi{} \; cm \) なので,
\( \pi{} \times 5^2 \times \dfrac{8\pi{}}{10\pi{}}=20\pi{} \; (cm^2) \)
【紫の面】
\( \pi{} \times 5^2-\pi{} \times 4^2=9\pi{} \; (cm^2) \)
よって,立体 \( X \) の表面積は,
\( 25\pi{}+30\pi{}+20\pi{}+9\pi{}=84\pi{} \; (cm^2) \)
大問3
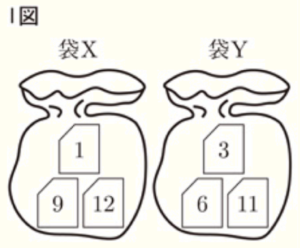
右のⅠ図のように,袋 \( X \) と袋 \( Y \) には,数が1つ書かれたカードがそれぞれ3枚ずつ入っている。袋 \( X \) に入っているカードに書かれた数はそれぞれ \( 1,9,12 \) であり,袋 \( Y \) に入っているカードに書かれた数はそれぞれ \( 3,6,11 \) である。
真人さんは袋 \( X \) の中から,有里さんは袋 \( Y \) の中からそれぞれ1枚のカードを同時に取り出し,取り出したカードに書かれた数の大きい方を勝ちとするゲームを行う。
このとき,次の問い (1)・(2) に答えよ。ただし,それぞれの袋において,どのカードが取り出されることも同様に確からしいものとする。
(1) 真人さんが勝つ確率を求めよ。
【解説】
真人さんが出すカードと有里さんが出すカードの組み合わせを樹形図として書き,
真人さんが勝つ組み合わせのところに
○ をつけてみます。
真人さんが勝つ組み合わせは5通り,すべての組み合わせは9通りなので,
求める確率は \( \dfrac{5}{9} \)

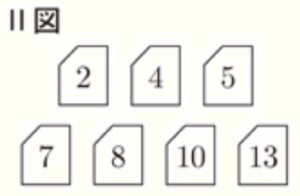
(2) 右のⅡ図のように,新たに,数が1つ書かれたカードを7枚用意した。これらのカードに書かれた数はそれぞれ \( 2,4,5,7,8,10,13 \) である。\( 4 \) と書かれたカードを袋 \( X \) に,\( 2,5,7,8,10,13 \) と書かれたカードのうち,いずれか1枚を袋 \( Y \) に追加してゲームを行う。
このとき,真人さんと有里さんのそれぞれの勝つ確率が等しくなるのは,袋 \( Y \) にどのカードを追加したときか,次の(ア)~(カ)からすべて選べ。
(ア) \( 2 \) (イ) \( 5 \) (ウ) \( 7 \) (エ) \( 8 \) (オ) \( 10 \) (カ) \( 13 \)
【解説】
まず,\( 4 \) と書かれたカードを袋 \( X \) に追加したとき,
真人さんが勝つ組み合わせと有里さんが勝つ組み合わせはそれぞれ6通りずつなので,
それぞれの勝つ確率は等しくなります。

ここから,袋 \( Y \) にカードを追加するとき,
真人さんと有里さんそれぞれの勝つ確率が等しくなるためには,
真人さんが勝つ組み合わせと有里さんが勝つ組み合わせが同じ数だけ増えればいいことになります。
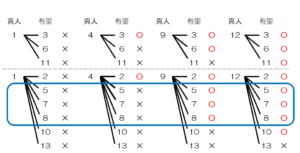
\( 2,5,7,8,10,13 \) のカードを追加したときの出すカードの組み合わせを樹形図に書いてみると,
\( 5,7,8 \) のカードを追加したときに,真人さんが勝つ組み合わせと有里さんが勝つ組み合わせが
2通りずつ増えることになります。
大問4
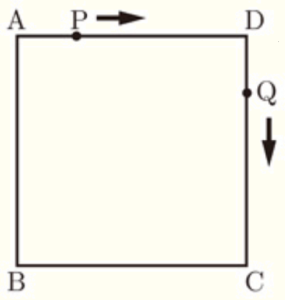
右の図のような,1辺が \( 6 \; cm \) の正方形 \( ABCD \) がある。点 \( P \) は,頂点 \( A \) を出発し,辺 \( AD \) 上を毎秒 \( 1 \; cm \) の速さで頂点 \( D \) まで進んで止まり,以後,動かない。また,点 \( Q \) は,点 \( P \) が頂点 \( A \) を出発するのと同時に頂点 \( D \) を出発し,毎秒 \( 1 \; cm \) の速さで正方形 \( ABCD \) の辺上を頂点 \( C \),頂点 \( B \) の順に通って頂点 \( A \) まで進んで止まり,以後,動かない。点 \( P \) が頂点 \( A \) を出発してから,\( x \) 秒後の \( △AQP \) の面積を \( y \; cm^2 \) とする。
このとき,次の問い(1)・(2)に答えよ。
(1) \( x=1 \) のとき,\( y \) の値を求めよ。また,点 \( Q \) が頂点 \( D \) を出発してから,頂点 \( A \) に到着するまでの \( x \) と \( y \) の関係を表すグラフとして最も適当なものを,次の(ア)~(エ)から1つ選べ。
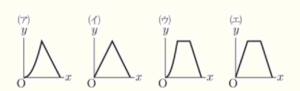
【解答】
\( y=\dfrac{1}{2} \)
(ウ)
【解説】
\( 0≦x≦6 \) の範囲では,\( AP=DQ=x \; cm \) なので,\( y=\dfrac{1}{2}x^2 \)
\( x=1 \) のとき,\( y=\dfrac{1}{2} \times 1^2=\dfrac{1}{2} \)
\( 6≦x≦12 \) の範囲では,底辺,高さともに \( 6 \; cm \) で一定なので,\( y=\dfrac{1}{2} \times 6^2=18 \)
\( 12≦x≦18 \) の範囲では,\( AP=6 \; cm \) で一定,\( AQ=18-x \; cm \) なので,\( y=-3x+54 \)
よって,あてはまるグラフは
(ウ)
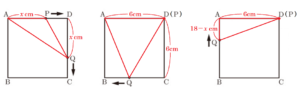
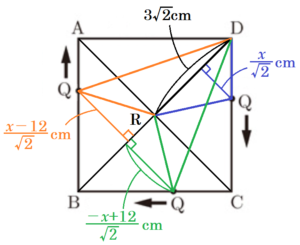
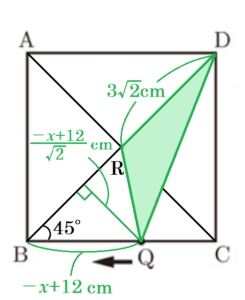
(2) 正方形 \( ABCD \) の対角線の交点を \( R \) とする。\( 0<x≦18 \) において,\( △RQD \) の面積が \( △AQP \) の面積と等しくなるような,\( x \) の値をすべて求めよ。
【解説】
\( △RQD \) について,底辺 \( DR \) は固定して,
点 \( Q \) の位置によって高さが変わると考えると,
\( 0<x≦6 \) のとき,
\( △RQD=3\sqrt{2} \times \dfrac{x}{\sqrt{2}} \times \dfrac{1}{2} \)
\( =\dfrac{3}{2}x \; (cm^2) \)
\( 6≦x≦12 \) のとき,
\( △RQD=3\sqrt{2} \times \dfrac{-x+12}{\sqrt{2}} \times \dfrac{1}{2} \)
\( =-\dfrac{3}{2}x+18 \; (cm^2) \)
\( 12≦x≦18 \) のとき,
\( △RQD=3\sqrt{2} \times \dfrac{x-12}{\sqrt{2}} \times \dfrac{1}{2} \)
\( =\dfrac{3}{2}x-18 \; (cm^2) \)
となります。
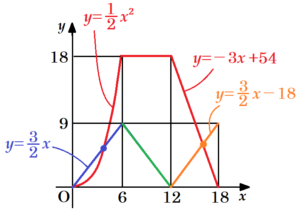
これらのグラフを(1)のグラフに書き加えると,
右のようなグラフになります。
このグラフにおいて,交点が \( △RQD \) の面積と \( △AQP \) の面積が等しくなるときを表しているので,
\( 0<x≦6 \) のとき,
\( \dfrac{1}{2}x^2=\dfrac{3}{2}x \)
\( x^2=3x \)
\( x(x-3)=0 \)
\( x=3 \) (\( 0<x≦6 \) より)
\( 12≦x≦18 \) のとき,
\( -3x+54=\dfrac{3}{2}x-18 \)
\( \dfrac{9}{2}x=72 \)
\( x=16 \)
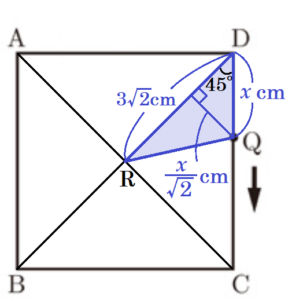
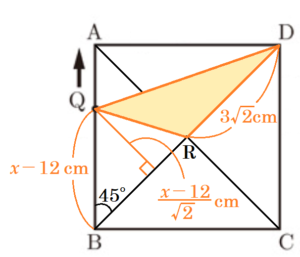
△RQDの面積の表し方
線分 \( DR \) を底辺と考え,点 \( Q \) から正方形 \( ABCD \) の対角線に垂線をひくと,
\( △RQD \) の高さになります。
また,その垂線と正方形 \( ABCD \) の辺の一部を1辺とする直角二等辺三角形ができるので,
辺の比から,垂線の長さを \( x \) を使って表すことができます。
【\( 0<x≦6 \) のとき】
\( DQ=x \; cm \) なので,垂線の長さは
\( \dfrac{DQ}{\sqrt{2}}=\dfrac{x}{\sqrt{2}} \; (cm) \)
よって,\( △RQD \) の面積は,
\( △RQD=3\sqrt{2} \times \dfrac{x}{\sqrt{2}} \times \dfrac{1}{2} \)
\( =\dfrac{3}{2}x \; (cm^2) \)
【\( 6≦x≦12 \) のとき】
\( BQ=-x+12 \; cm \) なので,垂線の長さは
\( \dfrac{BQ}{\sqrt{2}}=\dfrac{-x+12}{\sqrt{2}} \; (cm) \)
よって,\( △RQD \) の面積は,
\( △RQD=3\sqrt{2} \times \dfrac{-x+12}{\sqrt{2}} \times \dfrac{1}{2} \)
\( =-\dfrac{3}{2}x+18 \; (cm^2) \)
【\( 12≦x≦18 \) のとき】
\( BQ=x-12 \; cm \) なので,垂線の長さは
\( \dfrac{BQ}{\sqrt{2}}=\dfrac{x-12}{\sqrt{2}} \; (cm) \)
よって,\( △RQD \) の面積は,
\( △RQD=3\sqrt{2} \times \dfrac{x-12}{\sqrt{2}} \times \dfrac{1}{2} \)
\( =\dfrac{3}{2}x-18 \; (cm^2) \)
大問5
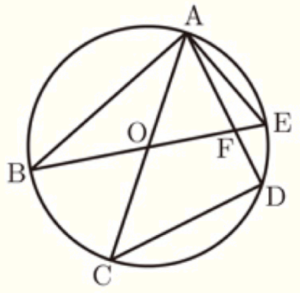
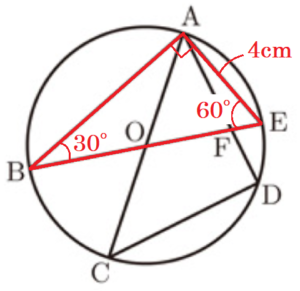
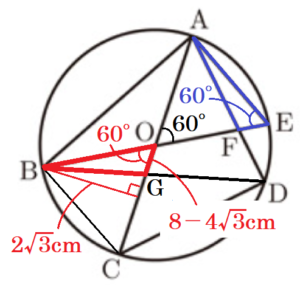
右の図のように,円 \( O \) の周上に5点 \( A,B,C,D,E \) がこの順にあり,線分 \( AC \) と線分 \( BE \) は円 \( O \) の直径である。また,\( AE=4 \; cm \) で,\( ∠ABE =30°,∠ACD=45° \) である。線分 \( AD \) と線分 \( BE \) との交点を \( F \) とする。
このとき,次の問い(1)~(3)に答えよ。
(1) 円 \( O \) の直径を求めよ。
【解説】
\( ∠BAE \) は直径 \( BE \) に対する円周角なので,
\( ∠BAE=90° \) であり,
\( △ABE \) は \( 30°,60°,90° \) の直角三角形になります。
よって,\( BE=2AE=8 \; cm \)
(2) 線分 \( EF \) の長さを求めよ。
【解答】
\( 8-4\sqrt{3} \; cm \)
【解説】
\( △OAB \) は \( OA=OB \) の二等辺三角形なので,
\( ∠OAB=∠OBA=30° \)
\( ∠CDA \) は直径 \( AC \) に対する円周角なので,
\( ∠CDA=90° \) であり,\( ∠ACD=45° \) より,
\( ∠CAD=180°-(90°+45°)=45° \)
ここから,
\( ∠BAF=30°+45°=75° \)
\( △BAF \) において,\( ∠BFA=180°-(30°+75°)=75° \) で,
\( ∠BAF=∠BFA=75° \) なので,
\( BA=BF \) の二等辺三角形になっています。
\( △ABE \) は \( 30°,60°,90° \) の直角三角形であり,\( AE=4 \; cm \) より,
\( AB=\sqrt{3}AE=4\sqrt{3} \; (cm) \)
なので,
\( BA=BF=4\sqrt{3} \; cm \)
よって,
\( EF=BE-BF=8-4\sqrt{3} \; (cm) \)
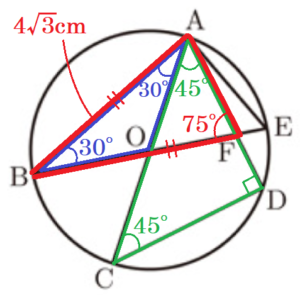
(3) 線分 \( AC \) と線分 \( BD \) との交点を \( G \) とするとき,\( △OBG \) の面積を求めよ。
【解答】
\( 8\sqrt{3}-12 \; cm^2 \)
【解説】
\( △OBG \) と \( △EAF \) において,
\( ∠OBG=∠EAF,∠AEF=∠BOG,BO=AE=4 \; cm \)
より,\( △OBG≡△EAF \)
対応する辺の長さは等しいので,(2)より,
\( OG=EF=8-4\sqrt{3} \; cm \)
\( △BOC \) は,
\( OA=OE=OB=OC=AE=4 \; cm \),
\( ∠BOC=∠AOE=∠AEO=60° \)
より,正三角形なので,
点 \( B \) から線分 \( AC \) に垂線をひき,交点を点 \( H \) とすると,
\( BO=4 \; cm \) より,\( BH=\dfrac{\sqrt{3}}{2}BO=2\sqrt{3} \; (cm) \)
よって,\( △OBG \) の面積は,
\( △OBG=OG \times BH \times \dfrac{1}{2} \)
\( =(8-4\sqrt{3}) \times 2\sqrt{3} \times \dfrac{1}{2} \)
\( =8\sqrt{3}-12 \; (cm^2) \)
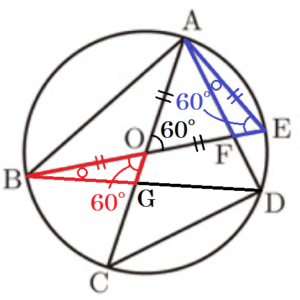
△OBG≡△EAFの証明
\( △OBG \) と \( △EAF \) において,
弧 \( DE \) に対する円周角なので,\( ∠OBG=∠EAF \) ・・・ ➀
\( OA=OE=AE=4 \; cm \) なので,
\( △OAE \) は正三角形であり,\( ∠AEF=∠AOE \)
対頂角は等しいので,\( ∠BOG=∠AOE \)
ここから,\( ∠AEF=∠BOG \) ・・・ ➁
また,\( BO=AE=4 \; cm \) ・・・ ③
➀➁③より,1組の辺とその両端の角がそれぞれ等しいので,
\( △OBG≡△EAF \)
大問6
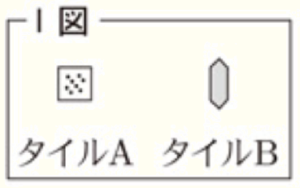
右のⅠ図のような,タイルAとタイルBが,それぞれたくさんある。タイルAとタイルBを,次のⅡ図のように,すき間なく規則的に並べたものを,1番目の図形,2番目の図形,3番目の図形,・・・ とする。
たとえば,2番目の図形において,タイルAは4枚,タイルBは12枚である。
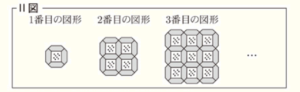
このとき,次の問い(1)~(3)に答えよ。
(1) 5番目の図形について,タイルAの枚数を求めよ。
【解説】
1番目の図形 ・・・ \( 1 \times 1=1 \)(枚)
2番目の図形 ・・・ \( 2 \times 2=4 \)(枚)
3番目の図形 ・・・ \( 3 \times 3=9 \)(枚)
4番目の図形 ・・・ \( 4 \times 4=16 \)(枚)
5番目の図形 ・・・ \( 5 \times 5=25 \)(枚)
(2) 12番目の図形について,タイルBの枚数を求めよ。
【解説】
縦1列の並び,横1列の並び(下の図のだ円1つ)をそれぞれ1グループと考えると,
1番目の図形 ・・・ \( 1 \)枚 \( \times \;\; 2 \)グループ \( \times \;\; 2 \)色 \( =4 \)(枚)
2番目の図形 ・・・ \( 2 \)枚 \( \times \;\; 3 \)グループ \( \times \;\; 2 \)色 \( =12 \)(枚)
3番目の図形 ・・・ \( 3 \)枚 \( \times \;\; 4 \)グループ \( \times \;\; 2 \)色 \( =24 \)(枚)
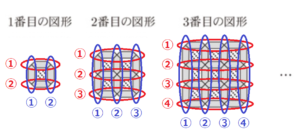
となるので,
12番目の図形 ・・・ \( 12 \)枚 \( \times \;\; 13 \)グループ \( \times \;\; 2 \)色 \( =312 \)(枚)
(3) \( n \) 番目の図形のタイルAの枚数とタイルBの枚数の差が \( 360 \) 枚であるとき,\( n \) の値を求めよ。
【解説】
(1)より,\( n \) 番目の図形のタイルAの枚数は,\( n^2 \) 枚
(2)より,\( n \) 番目の図形のタイルBの枚数は,\( 2n(n+1) \) 枚
と表すことができるので,
タイルAの枚数とタイルBの枚数の差が \( 360 \) 枚であるとき,
\( 2n(n+1)-n^2=360 \)
\( n^2+2n-360=0 \)
\( (n-18)(n+20)=0 \)
\( n=18,-20 \)
\( n>0 \) より,あてはまるのは \( n=18 \)

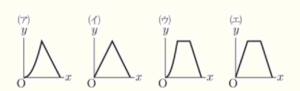


 \( y=\dfrac{16}{x} \) は反比例を表しているので,
\( y=\dfrac{16}{x} \) は反比例を表しているので,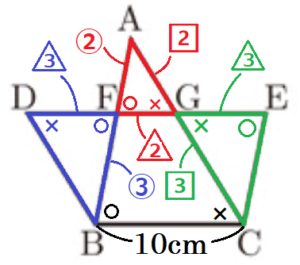
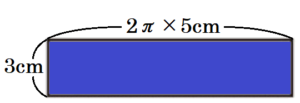






-アイキャッチ-120x68.jpg)
