大問1
(1)(ア)〜(エ)の計算をしなさい。
(ア) \( 4-11 \)
(イ) \( 4(2x+y)-3(x-3y) \)
【解説】
\( =8x+4y-3x+9y \)
\( =5x+13y \)
(ウ) \( (-6xy^3)÷(-2xy) \)
【解説】
\( =\dfrac{-6xy^3}{-2xy} \)
\( =3y^2 \)
(エ) \( \sqrt{27}-\sqrt{12} \)
【解説】
\( =3\sqrt{3}-2\sqrt{3} \)
\( =\sqrt{3} \)
(2) \( x^2-3x-40 \) を因数分解しなさい。
(3) 二次方程式 \( 3x^2+x-1=0 \) を解きなさい。
【解答】
\( x=\dfrac{-1±\sqrt{13}}{6} \)
【解説】
この二次方程式を \( ax^2+bx+c=0 \) と考えると,
\( a=3,b=1,c=-1 \) となるので,解の公式より,
\( x=\dfrac{-1±\sqrt{1^2-4 \times 3 \times (-1)}}{2 \times 3} \)
\( =\dfrac{-1±\sqrt{13}}{6} \)
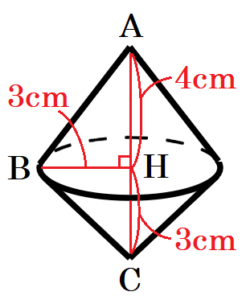
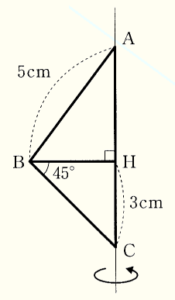
(4) 下の図のような \( △ABC \) がある。頂点 \( B \) から辺 \( AC \) に垂線をおろし,辺 \( AC \) との交点を \( H \) とする。\( AB=5 \; cm,CH=3 \; cm,∠CBH=45° \) であるとき,\( △ABC \) を,辺 \( AC \) を回転の軸として,1回転させてできる立体の体積を求めなさい。
【解答】
\( 21\pi{} \; cm^3 \)
【解説】
\( △BCH \) は,底角が \( 45° \) の直角三角形なので,
直角二等辺三角形であり,\( BH=CH=3 \; cm \) となっています。
\( △ABH \) は,\( AB=5 \; cm,BH=3 \; cm \) より,
\( 3:4:5 \) の直角三角形であり,\( AH=4 \; cm \) です。
ここから,1回転させてできる立体は,
底面の半径が \( 3 \; cm \),高さが \( 4 \; cm \) の円すい(円すい➀)と
底面の半径が \( 3 \; cm \),高さが \( 3 \; cm \) の円すい(円すい➁)
をくっつけたものになります。
円すい➀の体積 \( =(\pi{} \times 3^2) \times 4 \times \dfrac{1}{3}=12\pi{} \; (cm^3) \)
円すい➁の体積 \( =(\pi{} \times 3^2) \times 3 \times \dfrac{1}{3}=9\pi{} \; (cm^3) \)
なので,求める立体の体積は,\( 12\pi{}+9\pi{}=21\pi{} \; (cm^3) \)
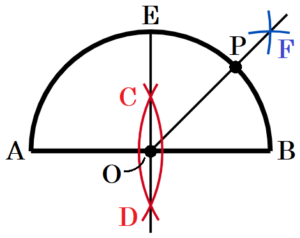
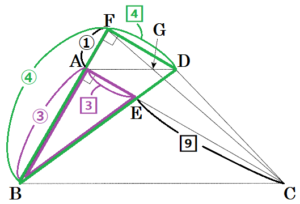
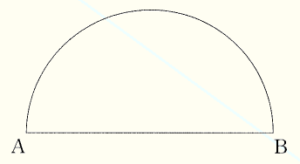
(5) 下の図のように,線分 \( AB \) を直径とする半円がある。弧 \( AB \) 上に,弧 \( AP: \)弧 \( PB=3:1 \) となるような点 \( P \) を作図しなさい。また,点 \( P \) の位置を示す文字 \( P \) も図の中にかき入れなさい。
ただし,作図には定規とコンパスを用い,作図に用いた線は消さずに残しておくこと。
【解答】
手順1 点 \( A,B \) を中心に円弧を描く。
(交点を点 \( C,D \) とします)
手順2 点 \( C,D \) を通る直線を描く。
(線分 \( AB \) との交点を点 \( O \),
弧 \( AB \) との交点を点 \( E \) とします)
手順3 点 \( B,E \) を中心に円弧を描く。
(交点を点 \( F \) とします)
手順4 点 \( O,F \) を通る直線を描く。
手順4の直線と弧 \( AB \) との交点が求める点 \( P \) となります。
【解説】
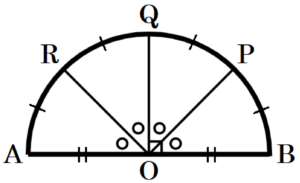
弧 \( AP: \)弧 \( PB=3:1 \) より,
右の図のように,弧 \( AP \) を3等分する点を
それぞれ点 \( Q,R \) とすると,
弧 \( AR= \)弧 \( RQ= \)弧 \( QP= \)弧 \( PB \)
となります。
この円の中心を点 \( O \) とすると,長さが等しい弧に対する中心角は等しいので,
\( ∠AOR=∠ROQ=∠QOP=∠POB=45° \)
であり,\( ∠QOB=90° \) となります。
このとき,\( OA=OB \) であることから,線分 \( OQ \) は「線分 \( AB \) の垂直二等分線 ・・・ ➀」になります。
また,\( ∠POB=45° \) であることから,線分 \( OP \) は 「\( ∠QOB \) の二等分線 ・・・ ➁」になります。
以上より,➀➁を描くことで点 \( P \) の位置がわかります。
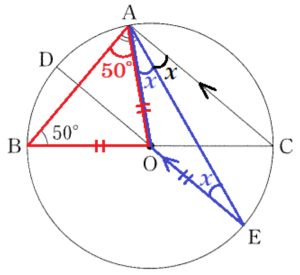
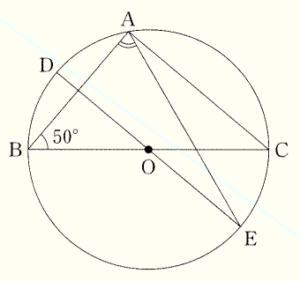
(6) 下の図のように,点 \( O \) を中心,線分 \( BC \) を直径とする円がある。この円周上に3点 \( A,D,E \) があり,線分 \( DE \) は点 \( O \) を通り,線分 \( AC \) と平行である。
このとき,\( ∠BAE \) の大きさを求めなさい。
【解説】
補助線 \( OA \) をひくと,
\( △OAB \) は二等辺三角形なので,
\( ∠OAB=∠OBA=50° \)
\( ∠OAE=x \) とすると,
\( △OAE \) は二等辺三角形なので,
\( ∠OEA=∠OAE=x \)
\( DE//AC \) より,錯角は等しいので,
\( ∠CAE=∠OEA=x \)
直径に対する円周角なので,\( ∠BAC=90° \) であり,
\( 50°+2x=90° \)
\( x=20° \)
よって,\( ∠BAE=50°+x=70° \)
(7) 下の図は1組から4組の各30人の生徒に対して数学のテストを行い,その得点をクラス別に箱ひげ図に表したものである。この箱ひげ図から読み取れることとして正しいものを,あとのア~オの中からすべて選び,記号を書きなさい。
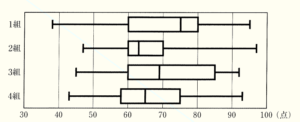
ア 1~4組全体の最高得点の生徒がいるのは2組である。
イ 平均点が最も高いのは3組である。
ウ 四分位範囲が最も大きいのは1組である。
エ 箱が示す区間に含まれているデータの個数は1組よりも2組の方が少ない。
オ 2組において,70点以上の人数は8人以上である。
【解説】
ア 最大値が最も大きいのは2組なので,正しい。
イ 箱ひげ図だけの情報では平均点はわからないので,間違い。
ウ 四分位範囲の大小は箱の長さで判断できます。箱の長さが最も長いのは3組なので,間違い。
エ 全体のデータの個数が等しいとき,箱が示す区間に含まれるデータの個数は等しくなるので,間違い。
オ 2組全体で30人なので,第3四分位数の値は点数が高い方から8番目の人の得点になります。
2組の第3四分位数の値は70点なので,正しい。
大問2
(1) アオイさんとリョウさんはバスケットボール部に所属しており,ある試合が終わった後に,次のような 【会話】をしている。
【会話】を踏まえて,(ア)~(ウ)の各問いに答えなさい。
【会話】
アオイ:今日の試合では,私たちのチームの得点は \( 61 \) 点だったね。
リョウ:コーチから聞いたけど,この試合では,シュートと得点が \( 1 \) 点のフリースローを合計 \( 85 \) 本放って
いて,シュートのうち \( 3 \) 点シュートと \( 2 \) 点シュートは同じ本数を放ったみたいだよ。チーム全体の
\( 3 \) 点シュートの成功率が \( 30 \; \% \),\( 2 \) 点シュートとフリースローの成功率はどちらも \( 40 \; \% \) だった
そうだよ。
アオイ:それぞれの種類のシュートとフリースローが何本成功したのかを計算してみよう。\( 3 \) 点シュートと
\( 2 \) 点シュートを放った本数をそれぞれ \( x \) 本,フリースローを放った本数を \( y \) 本として 【表】 の
ようにまとめたよ。

(ア) 【表】の中の \( \fbox{ ➀ } \) ~ \( \fbox{ ➂ } \) にあてはまる数や式の組み合わせとして正しいものを、次のア~エの中から1つ選び,記号を書きなさい。

(イ) \( x、y \) についての連立方程式を次のようにつくった。このとき,➃ と ➄ にあてはまる式を \( x、y \) を用いてそれぞれ表しなさい。
\( \left\{ \begin{array}{}
\fbox{ ➃ }=85 \\
\fbox{ ➄ }=61 \\
\end{array} \right. \)
【解答】
\( \fbox{ ➃ } \) ・・・ \( 2x+y \)
\( \fbox{ ➄ } \) ・・・ \( 3 \times \dfrac{30}{100}x+2 \times \dfrac{40}{100}x+1 \times \dfrac{40}{100}y \)
(ウ) この試合で,3点シュートは何本成功したか求めなさい。
【解説】
(イ)の連立方程式を解くと,
\( \left\{ \begin{array}{}
2x+y=85 \;\; ・・・ \;\; ➀ \\
3 \times \dfrac{30}{100}x+2 \times \dfrac{40}{100}x+1 \times \dfrac{40}{100}y=61 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁ を整理すると,
\( 17x+4y=610 \) ・・・ ➁’
➁’\( – \)➀\( \times 4 \)
\( 9x=270 \)
\( x=30 \)
ここから,3点シュートを放ったのは \( 30 \) 本で,そのうち \( 30 \; \% \) 成功したので,
成功したのは,\( 30 \times 0.3=9 \)(本)
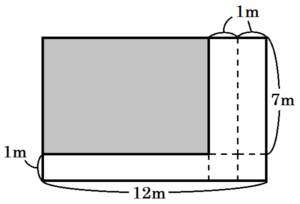
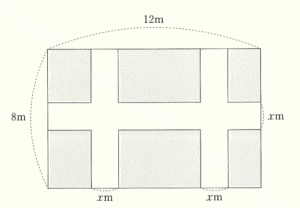
(2) 縦の長さが \( 8 \; m \),横の長さが \( 12 \; m \) の長方形の土地がある。下の図のように,縦に2本,横に1本の同じ幅の通路がある花だんをつくりたい。
通路の幅を \( x \; m \) とするとき,(ア)~(ウ)の各問いに答えなさい。
(ア) 通路の幅を \( 1 \; m \) とするとき,通路の面積を求めなさい。
【解説】
通路の位置を右と下の端にまとめると,
右の図のようになるので,
\( 1 \times 12+2 \times 7=26 \; (m^2) \)
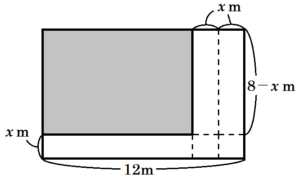
(イ) 通路の面積を,\( x \) を用いて表しなさい。
【解説】
問(ア)と同様に考えると,
\( x \times 12+2x \times (8-x)=12x+2x(8-x) \)
\( =-2x^2+28x \)
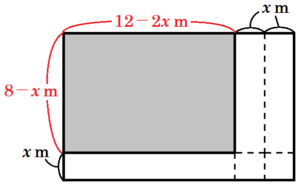
(ウ) 通路の面積と花だんの面積が等しいとき,通路の幅は何 \( m \) か求めなさい。
ただし,\( x \) についての方程式をつくり,答えを求めるまでの過程も書きなさい。
【解答】
通路の面積と花だんの面積が等しいので,
\( (8-x)(12-2x)=-2x^2+28x \)
\( 2x^2-28x+96=-2x^2+28x \)
\( 4x^2-56x+96=0 \)
\( x^2-14x+24=0 \)
\( (x-2)(x-12)=0 \)
\( x=2 \) ( \( 0<x<6 \) より)
よって, 通路の面積と花だんの面積が等しいときの通路の幅は \( 2 \; m \)
大問3
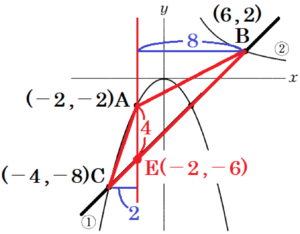
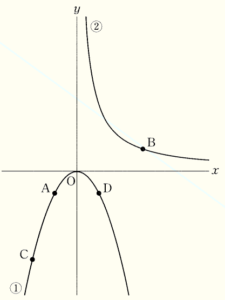
下の図のように,関数 \( y=ax^2 \) ・・・ ① のグラフは点 \( A(-2,-2) \) を通り,関数 \( y=\dfrac{b}{x} \; (x>0) \) ・・・ ② のグラフは点 \( B(6,2) \) を通る。関数 ① のグラフ上には2点 \( C,D \) があり,それぞれの \( x \) 座標は \( -4,2 \) である。
このとき,(1)~(7)の各問いに答えなさい。
(1) \( a \) の値を求めなさい。
【解答】
\( a=-\dfrac{1}{2} \)
【解説】
点 \( A(-2,-2) \) は \( y=ax^2 \) 上の点なので,
\( y=ax^2 \) に \( x=-2,y=-2 \) を代入すると,
\( -2=a \times (-2)^2 \)
\( a=-\dfrac{1}{2} \)
(2) \( b \) の値を求めなさい。
【解説】
点 \( B(6,2) \) は \( y=\dfrac{b}{x} \) 上の点なので,
\( y=\dfrac{b}{x} \) に \( x=6,y=2 \) を代入すると,
\( 2=\dfrac{b}{6} \)
\( b=12 \)
(3) 点 \( C \) の座標を求めなさい。
【解説】
点 \( C \) は \( y=-\dfrac{1}{2}x^2 \) 上の点で,\( x \) 座標は \( -4 \) なので,
\( y=-\dfrac{1}{2}x^2 \) に \( x=-4 \) を代入すると,
\( y=-\dfrac{1}{2} \times (-4)^2=-8 \)
(4) 直線 \( CD \) の式を求めなさい。
【解説】
点 \( D \) は \( y=-\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標は \( 2 \) なので,
\( y=-\dfrac{1}{2}x^2 \) に \( x=2 \) を代入すると,
\( y=-\dfrac{1}{2} \times 2^2=-2 \)
となり,点 \( D \) の座標は,\( D(2,-2) \)
直線 \( CD \) の式を \( y=cx+d \) とすると,
傾き \( c=\dfrac{-2-(-8)}{2-(-4)}=1 \)
\( y=x+d \) に \( x=2,y=-2 \) を代入すると,
\( -2=2+d \)
\( d=-4 \)
よって,直線 \( CD \) の式は \( y=x-4 \)
(5) 関数 ② のグラフ上には,\( x \) 座標と \( y \) 座標がともに自然数となるような点は何個あるか求めなさい。
【解説】
\( y=\dfrac{12}{x} \) において,\( x,y \) がともに自然数になるのは,
\( x \) の値が \( 12 \) の約数になるときです。
\( 12 \) の約数は,\( 1,2,3,4,6,12 \) の6個なので,
\( x \) 座標と \( y \) 座標がともに自然数となるような点は6個あることになります。
(6) \( △ABC \) の面積を求めなさい。
【解説】
\( B(6,2),C(-4,-8) \) より,
直線 \( BC \) の傾きは,
傾き \( =\dfrac{2-(-8)}{6-(-4)}=1 \)
であり,直線 \( BC \) と直線 \( CD \) は,
どちらも点 \( C \) を通り,傾きが \( 1 \) の直線になっています。
よって,3点 \( B,D,C \) は一直線上にあることになるので,
直線 \( BC \) の式は \( y=x-4 \) になります。
点 \( A(-2,-2) \) を通り \( y \) 軸に平行な直線と
直線 \( y=x-4 \) の交点を点 \( E \) とすると,
点 \( E \) の \( x \) 座標は \( -2 \) なので,
\( y=-2-4=-6 \)
となり,点 \( E \) の座標は,\( E(-2,-6) \)
\( △ABC=△ACE+△ABE \) なので,
\( △ACE=4 \times 2 \times \dfrac{1}{2}=4 \)
\( △ABE=4 \times 8 \times \dfrac{1}{2}=16 \)
\( △ABC=4+16=20 \)
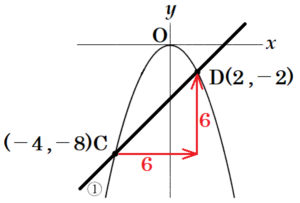
(7) 直線 \( BC \) 上に点 \( P \) をとる。\( △ACP \) の面積を \( S \),\( △ADP \) の面積を \( T \) とするとき,\( S:T=3:2 \) となるような点 \( P \) の \( x \) 座標をすべて求めなさい。
【解答】
\( x=-\dfrac{2}{5},14 \)
【解説】
3点 \( C,D,P \) は一直線上に並ぶことから,\( △ACP \) と \( △ADP \) は高さが等しいので,
\( △ACP:△ADP=3:2 \) となるとき,\( CP:DP=3:2 \) であり,
下の図のように,
3点 \( C,D,P \) が \( C,P,D \) の順番に並ぶ場合と \( C,D,P \) の順番に並ぶ場合
の2通りが考えられます。
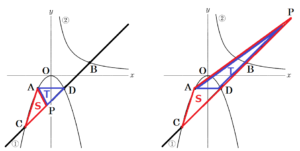
\( CP \) と \( DP \) の長さの比は,
3点 \( C,D,P \) の \( x \) 座標の値の差を使って求めることができます。
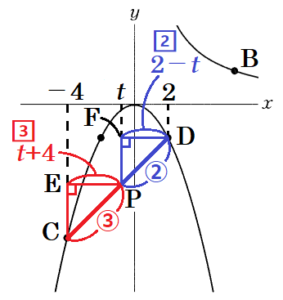
【 \( -4≦t≦2 \) の場合 】
点 \( P \) の \( x \) 座標の値を \( t \) とすると,
点 \( C \) の \( x \) 座標は \( -4 \),点 \( D \) の \( x \) 座標は \( 2 \) なので,
点 \( P \) が \( C,D \) の間にあるとき,\( -4≦t≦2 \) となります。
点 \( C \) を通り,\( y \) 軸に平行な直線と
点 \( P \) を通り,\( x \) 軸に平行な直線の交点を \( E \),
点 \( P \) を通り,\( y \) 軸に平行な直線と
点 \( D \) を通り,\( x \) 軸に平行な直線の交点を \( F \)
とすると,
\( △CEP \) ∽ \( △PFD \) なので,
\( CP:DP=PE:DF \)
\( 3:2=(t+4):(2-t) \)
\( 3(2-t)=2(t+4) \)
\( 5t=-2 \)
\( t=-\dfrac{2}{5} \)
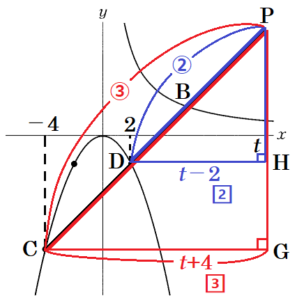
【 \( 2≦t \) の場合 】
\( C,D,P \) の順番に並ぶとき,\( 2≦t \) となります。
点 \( C \) を通り,\( x \) 軸に平行な直線と
点 \( P \) を通り,\( y \) 軸に平行な直線の交点を \( G \),
点 \( D \) を通り,\( x \) 軸に平行な直線と
点 \( P \) を通り,\( y \) 軸に平行な直線の交点を \( H \)
とすると,
\( △PCG \) ∽ \( △PDH \) なので,
\( CP:DP=CG:DH \)
\( 3:2=(t+4):(t-2) \)
\( 3(t-2)=2(t+4) \)
\( t=14 \)
大問4
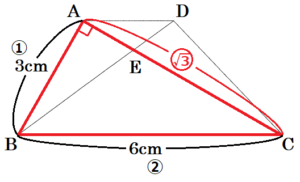
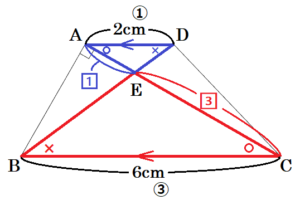
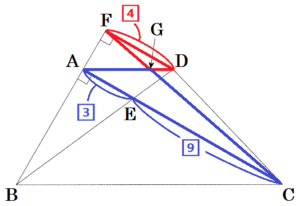
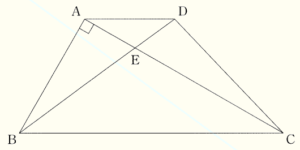
下の図のように,\( AD//BC,AD=2 \; cm \),
\( BC=6 \; cm,AB=3 \; cm \) の台形 \( ABCD \) がある。線分 \( AC \) と線分 \( BD \) の交点を \( E \),\( ∠BAE=90° \) とする。
このとき,(1)~(3)の各問いに答えなさい。
(1) 線分 \( AC \) の長さを求めなさい。
【解答】
\( 3\sqrt{3} \; cm \)
【解説】
\( BC=6 \; cm,AB=3 \; cm,∠BAE=90° \) より,
\( △ABC \) は,3辺の長さが
\( AB:BC:AC=1:2:\sqrt{3} \)
の直角三角形なので,
\( AC=\sqrt{3}AB=3\sqrt{3} \; (cm) \)
(2) 線分 \( CE \) の長さを求めなさい。
【解答】
\( \dfrac{9\sqrt{3}}{4} \; cm \)
【解説】
\( AD//BC \) より,\( △BCE \) ∽ \( △DAE \) なので,
\( AD=2 \; cm,BC=6 \; cm \) より,
\( CE:AE=BC:DA=6:2=3:1 \)
であり,
\( CE=\dfrac{3}{4}AC=\dfrac{9\sqrt{3}}{4} \; (cm) \)
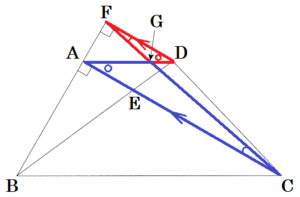
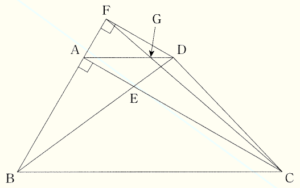
(3) 点 \( D \) を通り直線 \( AC \) に平行な直線と,直線 \( AB \) との交点を \( F \) とする。また,線分 \( CF \) と線分 \( AD \) との交点を \( G \) とする。
このとき,(ア)~(ウ)の各問いに答えなさい。
(ア) \( △DFG \) ∽ \( △ACG \) であることを証明しなさい。
【解答】
\( △DFG \) と \( △ACG \) において
\( DF//AC \) より,錯角は等しいので,
\( ∠GDF=∠GAC \) ・・・ ➀
\( ∠GFD=∠GCA \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △DFG \) ∽ \( △ACG \)
(イ) \( △DFG \) の面積を \( S \) とするとき,\( △ACG \) の面積を,\( S \) を用いて表しなさい。
【解説】
(ア)より,\( △DFG \) ∽ \( △ACG \) であることがわかっているので,
相似比を求めることができれば,面積比を求めることができます。
\( △ABC \) と \( △CAD \) は高さが共通なので,
\( AD=2 \; cm,BC=6 \; cm \) より,
\( △ABC:△CAD=6:2=3:1 \)
\( DF//AC \) より,等積変形の考え方から,
\( △CAF=△CAD \) なので,
\( △ABC:△CAF=3:1 \)
\( △ABC \) と \( △CAF \) は高さが共通なので,
\( BA:AF=△ABC:△CAF=3:1 \)
\( AE//DF \) より,\( △BAE \) ∽ \( △BFD \) なので,
\( AE:FD=BA:BF=3:4 \)
(2)より,\( CE:AE=3:1=9:3 \)
(3-ア)より,\( △DFG \) ∽ \( △ACG \) であり,
相似比は,\( FD:CA=4:12=1:3 \)
相似な三角形の面積比は,相似比の2乗の比になるので,
\( △DFG:△ACG=1^2:3^2=1:9 \)
よって,\( △DFG \) の面積を \( S \) とするとき,\( △ACG \) の面積は \( 9S \)
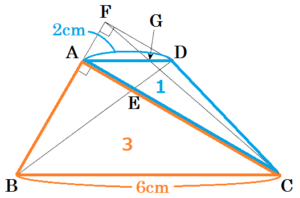
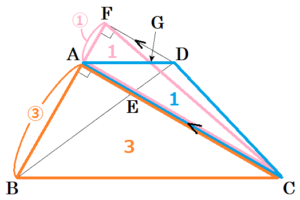
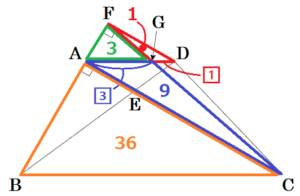
(ウ) \( △DFG \) の面積を \( S \),\( △BCD \) の面積を \( T \) とするとき,\( S:T \) を最も簡単な整数の比で表しなさい。
【解説】
\( △DFG \) ∽ \( △ACG \) で,相似比は \( 1:3 \) なので,
\( DG:AG=1:3 \)
\( △DFG \) と \( △ACG \) は高さが共通なので,
\( △DFG:△AFG=DG:AG=1:3 \) ・・・ ➀
また,(イ)より,
\( △DFG:△ACG=1:9 \) ・・・ ➁ なので,
➀➁より,
\( △DFG:△CAF=1:12 \) ・・・ ➂
\( △ABC:△CAF=3:1 \) ・・・ ➃ なので,
➂➃より,
\( △DFG:△ABC=1:36 \) ・・・ ➄
\( AD//BC \) より,等積変形の考え方から,
\( △BCD=△ABC \) なので,
\( △DFG:△BCD=1:36 \)
よって,\( S:T=1:36 \)
大問5
(1) 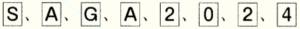 と書かれた合計8枚のカードがある。アルファベットが書かれたカード4枚 (
と書かれた合計8枚のカードがある。アルファベットが書かれたカード4枚 ( ) は 【図1】 のようにこの順に机の上に並べ,数字が書かれたカード4枚 (
) は 【図1】 のようにこの順に机の上に並べ,数字が書かれたカード4枚 (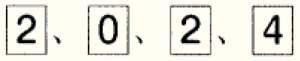 ) は 【図2】 のように袋の中に入れる。
) は 【図2】 のように袋の中に入れる。
下の 【操作】 を2回行うとき, 【例】 を参考にして,(ア)~(エ)の各問いに答えなさい。
ただし,どのカードの取り出し方も同様に確からしいとし,取り出したカードはもとにもどさない。また, 【操作】 によって回転させたカードはもとにもどさない。
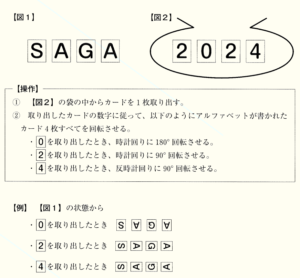
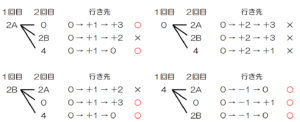
(ア) 【図1】 の状態から2回 【操作】 を行った。取り出したカードが1回目に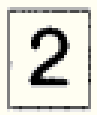 ,2回目に
,2回目に のカードであったとき,アルファベットが書かれたカードの状態として正しいものを,次のア~エの中から1つ選び,記号を書きなさい。
のカードであったとき,アルファベットが書かれたカードの状態として正しいものを,次のア~エの中から1つ選び,記号を書きなさい。
ア 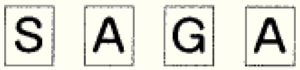 イ
イ 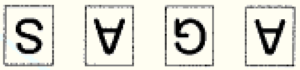
ウ 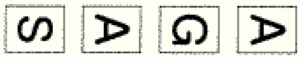 エ
エ 
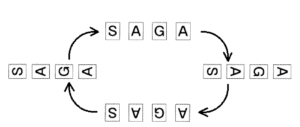
【解説】
1回目の
【操作】 で時計回りに \( 90° \),2回目の
【操作】 で時計回りに \( 180° \) 回転させることになります。
(イ) 2回 【操作】 を行うとき,1度も のカードを取り出さない確率を求めなさい。
のカードを取り出さない確率を求めなさい。
【解説】
袋に入っている2枚の
のカードに「2A」,「2B」と名前をつけて
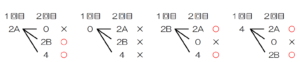
2枚のカードを選ぶ組み合わせを樹形図に書き出し,

のカードを含まないところに
○ をつけると,
「0」を含まない組み合わせは6通り,すべての組み合わせは12通りなので,
求める確率は,\( \dfrac{6}{12}=\dfrac{1}{2} \)
(ウ) 【図1】 の状態から2回 【操作】 を行った後,アルファベットが書かれたカードの状態が となる確率を求めなさい。
となる確率を求めなさい。
【解説】
【図1】 の状態のカードの向きを \( 0 \) とし,
時計回りに \( 90° \) 回転させることを \( +1 \),反時計回りに \( 90° \) 回転させることを \( -1 \) とすると,
2回の操作の合計が \( +3 \) または \( -1 \) となるとき,

のカードの向きになります。
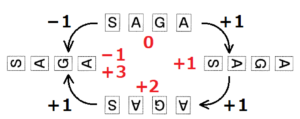
2回の操作の合計が \( +3 \) または \( -1 \) となるのは,
と

のカードを1回ずつ取り出すときなので,
あてはまる組み合わせは4通り,すべての組み合わせは12通りなので,
求める確率は,\( \dfrac{4}{12}=\dfrac{1}{3} \)

(エ) 【図1】 の状態から2回 【操作】 を行うとき,1回目の操作後と2回目の操作後で,アルファベットが書かれたカードの状態が1度も とならない確率を求めなさい。
とならない確率を求めなさい。
【解説】
2枚のカードを選ぶ組み合わせとそれぞれの場合でのカードの向きを樹形図に書き出し,
「+2」を含まないところに
○ をつけてみると,
「+2」を含まない組み合わせは7通り,すべての組み合わせは12通りなので,
求める確率は,\( \dfrac{7}{12} \)
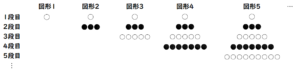
(2) 白い石と黒い石を,次の 【ルール】 に従って,下のように並べていく。また,あとの 【表】 は,白い石の個数を \( X \),黒い石の個数を \( Y \) として,白い石の個数から黒い石の個数を引いた \( X-Y \) の値についてまとめたものである。
このとき,(ア)~(エ)の各問いに答えなさい。
【ルール】
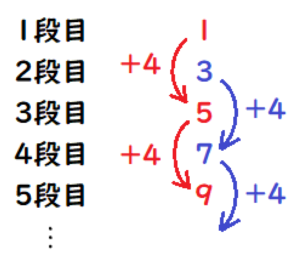
・1段目に,白い石を1個置いたものを図形1とする。
・図形1に続けて,2段目に,黒い石を3個並べたものを図形2とする。
・図形2に続けて,3段目に,白い石を5個並べたものを図形3とする。
・以下繰り返して,図形 \( n \) に続けて,\( (n+1) \) 段目に,\( n \) 段目と色の異なる石を\( (2n+1) \) 個並べたものを図形 \( (n+1) \) とする。 ただし,\( n \) は自然数とする。
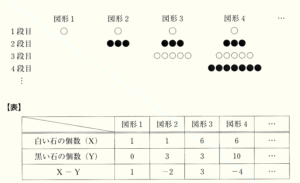
(ア) 図形5のとき,\( X \) の値を求めなさい。
(イ) 図形6のとき,\( X-Y \) の値を求めなさい。
【解説】
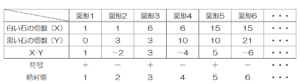
【表】の \( X-Y \) の値は,図形1から図形4まで
符号は+と-を順番に繰り返し,絶対値は \( 1 \) ずつ増えています。
よって,図形6のときの \( X-Y \) の値は, \( -6 \)
(ウ) \( X-Y=9 \) のとき,\( X \) の値を求めなさい。
【解説】
(イ)の考え方から,\( X-Y=9 \) になるのは,図形9のときであり,
図形9は9段でできた図形になります。
\( X \) の値が増えるのは,3段目,5段目と奇数段目のときです。
また,白い石の個数は1段目の1個から始まって,3段目では5個,
5段目では9個増えているので,7段目では13個,9段目では17個増えることになります。
よって,図形9における白い石の個数 \( (X) \) は,
\( X=1+5+9+13+17=45 \)(個)
(エ) \( X+Y=225 \) のとき,\( X \) と \( Y \) の値を求めなさい。
【解説】
【表】の \( X-Y \) のところを \( X+Y \) に書き直してみると,\( n \) 番目の図形の値は \( n^2 \) になっていて,
\( 225=15 \times 15 \) なので,\( X+Y=225 \) になるのは図形15のときになります。
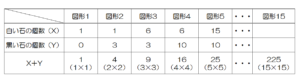
\( n \) 段目に並ぶ白い石の個数は,\( 2n-1 \) 個なので,
図形15,つまり,15段でできた図形の
15段目に並ぶ白い石の個数は,
\( 2 \times 15-1=29 \)(個)になります。
ここから,図形15の白い石の個数 \( (X) \) は,
\( X=1+5+9+13+17+21+25+29=120 \)(個)
このとき,黒い石の個数 \( (Y) \) は,
\( Y=225-120=105 \)(個)




![]() と書かれた合計8枚のカードがある。アルファベットが書かれたカード4枚 (
と書かれた合計8枚のカードがある。アルファベットが書かれたカード4枚 (![]() ) は 【図1】 のようにこの順に机の上に並べ,数字が書かれたカード4枚 (
) は 【図1】 のようにこの順に机の上に並べ,数字が書かれたカード4枚 (![]() ) は 【図2】 のように袋の中に入れる。
) は 【図2】 のように袋の中に入れる。
![]() ,2回目に
,2回目に![]() のカードであったとき,アルファベットが書かれたカードの状態として正しいものを,次のア~エの中から1つ選び,記号を書きなさい。
のカードであったとき,アルファベットが書かれたカードの状態として正しいものを,次のア~エの中から1つ選び,記号を書きなさい。![]() イ
イ ![]()
![]() エ
エ ![]()
![]() のカードを取り出さない確率を求めなさい。
のカードを取り出さない確率を求めなさい。![]() となる確率を求めなさい。
となる確率を求めなさい。![]() とならない確率を求めなさい。
とならない確率を求めなさい。