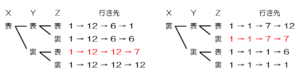大問１
問１ （１）～（３）の計算をしなさい。
（１） \( (-1)+(-5) \)
（２） \( 7+18 \div (-3) \)
（３） \( \sqrt{6} \times \sqrt{3}-\sqrt{2} \)
問２ \( 70 \) を素因数分解しなさい。
問３ \( 1 \; m \) あたりの重さが \( 30 \; g \) の針金があります。この針金 \( x \; m \) の重さが \( y \; g \) であるとき，\( y \) を \( x \) の式で表しなさい。
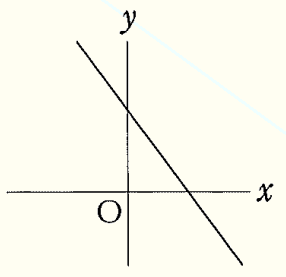
問４ 右の図のような関数 \( y=ax+b \) のグラフがあります。点 \( O \) は原点とします。\( a \) と \( b \) の値について，次のように説明するとき，①，②の｛ ｝に当てはまるものを，それぞれア〜ウから選びなさい。
\( a \) の値は ①｛ア 正の数 イ \( 0 \) ウ 負の数｝であり，
\( b \) の値は ②｛ア 正の数 イ \( 0 \) ウ 負の数｝である。
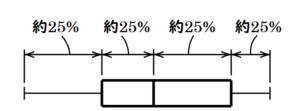
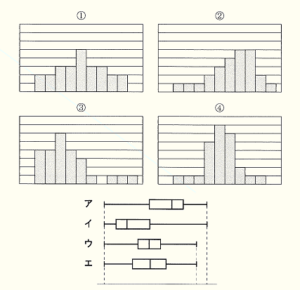
問５ 下の①～④のヒストグラムは，それぞれア～エのいずれかの箱ひげ図と同じデータを
使ってまとめたものです。①，②のヒストグラムは，どの箱ひげ図と同じデータを使って
まとめたものですか。最も適当なものを，それぞれア～エから選びなさい。
・ 左側の棒の部分（最小値と第一四分位数の間）
・ 箱の左側（第一四分位数と中央値の間）
・ 箱の右側（中央値と第三四分位数の間）
・ 右側の棒の部分（第三四分位数と最小値の間）
にはそれぞれ約２５％の個数のデータが含まれます。
（例：データの総数が２０個であれば，５個ずつのデータが含まれます）
ここから，棒の長さや箱の長さが短いほど，その中に含まれる階級の度数が大きいことになります。
左側の棒の部分を「Ａ」，箱の左側の部分の部分を「Ｂ」，箱の右側の部分の部分を「Ｃ」，
右側の棒の部分を「Ｄ」とすると，
イの箱ひげ図は，Ｃ，Ｄの部分と比べて，Ａ，Ｂの部分の長さが短くなっていて，
全体の左半分に箱が含まれているので，
ヒストグラムでは半分より左側に山ができ（度数が大きくなり）ます。
ここから，あてはまるヒストグラムは➁であるとわかります。
アの箱ひげ図は，Ａ，Ｂ，Ｄの部分と比べて，Ｃの部分の長さが短くなっていて，
全体の右半分に箱のほとんどの部分が含まれているので，
ヒストグラムでは半分より右側に山ができます。
ここから，あてはまるヒストグラムは➁であるとわかります。
ウの箱ひげ図は，Ａ，Ｄの部分と比べて，Ｂ，Ｃの部分の長さが短くなっていて，
箱ひげ図はほぼ左右対称なので，
ヒストグラムでは中央付近に山ができます。
ここから，あてはまるヒストグラムは➃であるとわかります。
エの箱ひげ図は，Ａ，Ｂ，Ｃ，Ｄの部分がほぼ均等（ややＢ，Ｃが短い）になっているので，
ヒストグラムでは全体の高さがほぼ平らになります。
ここから，あてはまるヒストグラムは➀であるとわかります。
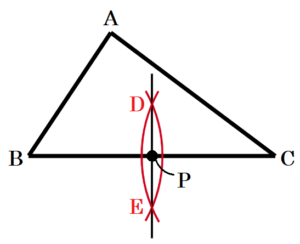
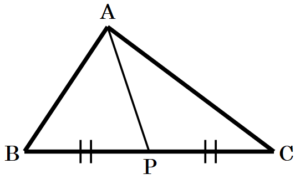
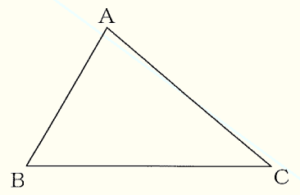
問６ 下の図のような \( △ABC \) があります。辺 \( BC \) 上に点 \( P \) を，\( △ABP \) と \( △ACP \) の面積が等しくなるようにとります。点 \( P \) を定規とコンパスを使って作図しなさい。
ただし，点を示す記号 \( P \) をかき入れ，作図に用いた線は消さないこと。
手順１ 点 \( B，C \) を中心に円弧を描く。
（交点を点 \( D，E \) とします。）
手順２ 点 \( D，E \) を通る直線を描く。
手順２の直線と辺 \( BC \) の交点が求める点 \( P \) になります。
点 \( P \) は，辺 \( BC \) 上の点であることから，
\( △ABP \) と \( △ACP \) は高さが等しいので，
\( △ABP \) と \( △ACP \) の面積が等しくなるとき，
\( BP=CP \) となります。
よって，辺 \( BC \) の垂直二等分線を描くことで，
\( BP=CP \) となる点 \( P \) を求めることができます。
大問２
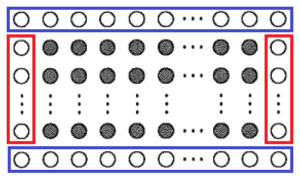
勇太さんは，自宅の花だんに，赤色と白色のチューリップを植えることにしました。花だんの形が長方形であることから，勇太さんは，右の図のように，条件にしたがってチューリップを等間隔に並べたいと考えています。
次の問いに答えなさい。
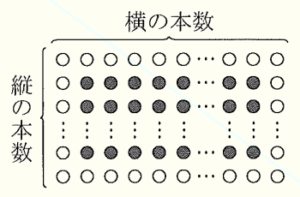
・ 赤色のチューリップの周囲に1列で白色のチューリップを並べる。
・ 白色のチューリップの横の本数が，縦の本数の2倍となるように並べる。
問１ 勇太さんは，白色のチューリップの本数の求め方について，ノートにまとめました。
次の（１），（２）に答えなさい。
(勇太さんのノート)
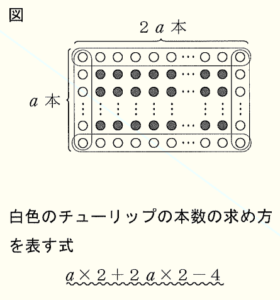
説明
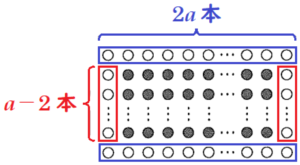
白色のチューリップの縦の本数を \( a \) 本とする。図のように，白色のチューリップを線で囲むと，１つの縦の囲みに \( a \) 本，１つの横の囲みに \( 2a \) 本ある。縦，横の囲みは２つずつあるから，この４つの囲みの中の本数の合計は，\( a×2+2a×2 \) で表される。
このとき，２回数えている白色のチューリップが \( 4 \) 本あるので， \( a×2+2a×2 \) から \( 4 \) をひく。
（１） 白色のチューリップの縦の本数が \( 6 \) 本のとき，白色のチューリップの本数を求めなさい。
（２） 白色のチューリップの縦の本数を \( a \) 本として，勇太さんとは異なる求め方で白色のチューリップの本数を求めるとき，解答用紙の図に囲みをかき入れ，その囲みをもとにして，白色のチューリップの本数の求め方を表す式を，下線部
のように，\( a \) を用いて書きなさい。
横に \( 2a \) 本の囲みをつくると，縦の囲みには \( a-2 \) 本が入ります。
縦，横の囲みは２つずつあるので，合計の本数は，
\( (a-2) \times 2+2a \times 2 \)（本）
と表すことができます。
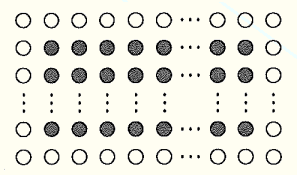
問２ 勇太さんが,条件にしたがってチューリップを植えたところ，チューリップは全部で \( 242 \) 本になりました。 このときの赤色のチューリップの本数を求めなさい。
大問３
ユキさんたちのクラスでは，数学の授業で，関数のグラフについてコンピュータを使って学習をしています。
次の問いに答えなさい。
問１ 先生が提示した画面１には，関数 \( y=x^2 \) のグラフと，このグラフ上の２点 \( A，B \) を通る直線が表示されています。点 \( A \) の \( x \) 座標は \( 3 \)，点 \( B \) の \( x \) 座標は \( -2 \) です。点 \( O \) は原点とします。
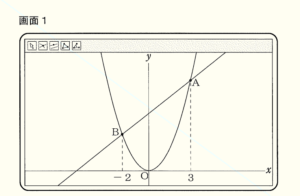
ユキさんは，画面１を見て，２点 \( A，B \) を通る直線の式を求めたいと考え，求め方について，次のような見通しを立てています。
２点 \( A，B \) を通る直線の式を求めるには，２点 \( A，B \) の座標がわかればよい。
（１） 点 \( A \) の \( y \) 座標を求めなさい。
（２） ユキさんの見通しを用いて，２点 \( A，B \) を通る直線の式を求めなさい。
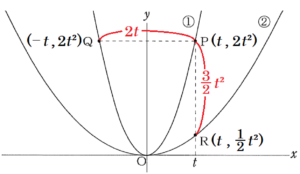
問２ 先生が提示した画面２には，２つの関数 \( y=2x^2 \) ･･･ ①，\( y=\dfrac{1}{2}x^2 \) ･･･ ② のグラフが表示されています。① のグラフ上に点 \( P \) があり，点 \( P \) の \( x \) 座標は \( t \) です。点 \( Q \) は，点 \( P \) と \( y \) 軸について対称な点です。また，点 \( R \) は，点 \( P \) を通り，\( y \) 軸に平行な直線と ② のグラフとの交点です。点 \( O \) は原点とし，\( t>0 \) とします。
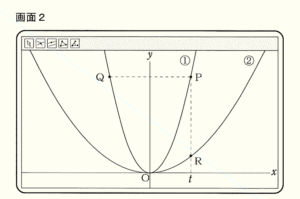
ユキさんたちは，点 \( P \) を ① のグラフ上で動かすことで，\( △PQR \) がどのように変化するかについて，話し合っています。
ルイさん 「このとき，\( △PQR \) はいつでも直角三角形になるね。」
ユキさん 「・・・あれ？\( △PQR \) が直角二等辺三角形に見えるときがあるよ。」
ルイさん 「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん 「じゃあ，\( △PQR \) が直角二等辺三角形になるときの点 \( P \) の座標を求めてみようか。」
ルイさん 「点 \( P \) の座標を求めるには，\( t \) の値がわかればいいね。」
点 \( R \) は，\( y=\dfrac{1}{2}x^2 \) 上の点で，\( x \) 座標は \( t \) なので，\( y=\dfrac{1}{2}t^2 \) であり，\( R \left( t，\dfrac{1}{2}t^2 \right) \)
点 \( Q \) は，点 \( P \) と \( y \) 軸について対称な点なので，\( Q(-t，2t^2) \)
ここから，
\( PR=2t^2-\dfrac{1}{2}t^2=\dfrac{3}{2}t^2 \)
\( PQ=t-(-t)=2t \)
なので，
\( \dfrac{3}{2}t^2=2t \)
\( 3t^2=4t \)
\( t(3t-4)=0 \)
\( t=\dfrac{4}{3} \) ( \( t>0 \) より)
大問４
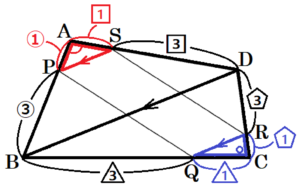
図１のように，四角形 \( ABCD \) があり，辺 \( AB \)，\( BC，CD，DA \) 上の点をそれぞれ \( P，Q，R，S \) とします。亜季さんたちは，「４点 \( P，Q，R，S \) が各辺の中点であるとき，四角形 \( PQRS \) は，いつでも平行四辺形になる」 ということを授業で学習しました。
次の問いに答えなさい。
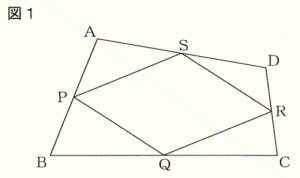
問１ 亜季さんは，４点 \( P，Q，R，S \) を各辺の中点としたまま，四角形 \( ABCD \) がいろいろな
ひし形となるように，コンピュータを使って四角形 \( ABCD \) の形を変え，四角形 \( PQRS \)
の形を調べたところ，次のことがらに気づき，ノートにまとめました。
四角形 \( ABCD \) がひし形ならば，四角形 \( PQRS \) は，いつでも である。
に言葉を当てはめるとき，このことがらが成り立たないものを，ア〜ウからすべて選びなさい。
ア 正方形 イ 長方形 ウ ひし形
ひし形の対角線は垂直に交わるので，\( AC⊥BC \) であり，
中点連結定理より，\( PQ//RS//AC，PS//QR//BD \) なので，
\( PQ⊥PS，PQ⊥QR，RS⊥QR，RS⊥PS \)
となります。
ここから，四角形 \( PQRS \) は，イ 長方形になるとわかります。
また，図のように４辺の長さが等しくなるとは限らないので，
ア 正方形，ウ ひし形 はあてはまらないとわかります。
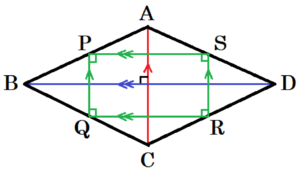
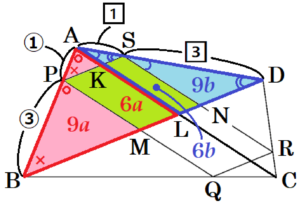
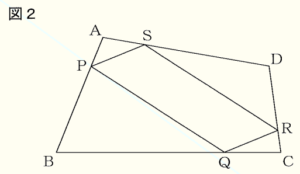
問２ 大地さんは，四角形 \( ABCD \) の各辺における４点 \( P，Q，R，S \) のとり方に着目し，コンピュータを使って，図２のように，この４点を各辺の辺上で動かしました。
大地さんは，「 \( AP：PB=CQ：QB=CR：RD=AS：SD=1：3 \) のとき，四角形 \( PQRS \) は平行四辺形である」 と予想しました。
次の（１），（２）に答えなさい。
（１） 大地さんの予想が成り立つことを証明しなさい。
\( △APS \) と \( △ABD \) において，
\( AP：PB=1：3 \)より，\( AP：AB=1：4 \)･･･➀
\( AS：SD=1：3 \)より，\( AS：AD=1：4 \)･･･➁
\( ∠A \) は共通 ･･･ ➂
➀➁➂より，２組の辺の比とその間の角がそれぞれ等しいので，\( △APS \) ∽ \( △ABD \)
対応する辺の比は等しいので，\( PS：BD=1：4 \) であり，\( PS=\dfrac{1}{4}BD \) ･･･ ➃
また，➀➁より，\( PS//BD \) ･･･ ➄
\( △CQR \) と \( △CBD \) において，
\( CQ：QB=CR：RD=1：3 \) なので，
\( △APS \) と \( △ABD \) の場合と同様の考え方から，
\( QR=\dfrac{1}{4}BD \) ･･･ ⑥
\( QR//BD \) ･･･ ➆
➃➅より，\( PS=QR \) ･･･ ⑧
➄➆より，\( PS//QR \) ･･･ ➈
⑧➈より，１組の向かい合う辺が平行で長さが等しいので，
四角形 \( PQRS \) は平行四辺形である
（２） 四角形 \( ABCD \) の対角線 \( BD \) と，線分 \( PQ，RS \) との交点をそれぞれ \( M，N \) とします。\( △APS \) の面積が \( 3 \; cm^2 \) であるとき，四角形 \( PMNS \) の面積を求めなさい。
ただし，四角形 \( PQRS \) は平行四辺形であることがわかっています。
\( △APK \) の面積を \( a \)，\( △ASK \) の面積を \( b \) とします。
\( △APK \) ∽ \( △ABL \) で，相似比は \( 1：4 \) なので，
\( △ABL \) の面積は，\( 16a \) と表すことができます。
また，
\( AC//PQ \) より，\( ∠KAP=∠MPB \)
\( PS//BD \) より，\( ∠APK=∠PBM \)
であり，\( △APK \) ∽ \( △PBM \)
相似比は，\( AP：PB=1：3 \) なので，
\( △PBM \) の面積は，\( 9a \) と表すことができます。
ここから，
四角形 \( PMLK=△ABL-(△APK+△PBM)=6a \)
同様の考え方から，
四角形 \( SNLK=△ADL-(△ASK+△SDN)=6b \)
\( △APS=a+b=3 \; (cm^2) \) より，
四角形 \( PQRS= \) 四角形 \( PMLK+ \) 四角形 \( SNLK \)
\( =6a+6b \)
\( =6(a+b) \)
\( =6 \times 3 \)
\( =18 \; (cm^2) \)
大問５
図１のような頂角が \( 120° \) の二等辺三角形があります。
次の問いに答えなさい。
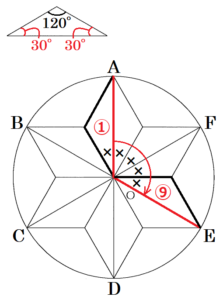
問１ 図２のように，円 \( O \) の円周を６等分する点 \( A，B，C，D，E，F \) があり，図１と合同な二等辺三角形 ①〜⑫ を，それぞれの三角形の最も長い辺が円 \( O \) の半径となるように並べます。
次の（１），（２）に答えなさい。
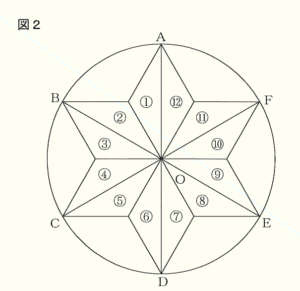
（１） ① を，点 \( O \) を中心として時計回りに回転移動して，⑨ に初めてぴったり重なったのは，何度回転移動したときですか。その角度を求めなさい。
➀ が ➈ とぴったり重なるのは線分 \( OA \) が線分 \( OE \) と重なるまで回転させたときなので，
二等辺三角形の底角４個分になります。
図１の二等辺三角形の底角は
\( \dfrac{180°-120°}{2}=30° \)
なので，求める角度は，\( 30° \times 4=120° \)
（２） 種類の異なる３枚の硬貨 \( X，Y，Z \) があります。硬貨 \( X，Y，Z \) を同時に投げ，表と裏の出かたに応じて，① に，次の１～３の操作を順に行い，最後に ①～⑫ のどの三角形に重なるかを調べます。
１ 硬貨 \( X \) が表のときは線分 \( AD \) を対称の軸として対称移動させ，裏のときは移動させない。
２ 硬貨 \( Y \) が表のときは点 \( O \) を回転の中心として \( 180° \) 回転移動させ，裏のときは移動
させない。
３ 硬貨 \( Z \) が表のときは平行移動してぴったりと重なる三角形に移動させ，裏のときは移動させない。
３枚の硬貨 \( X，Y，Z \) を同時に投げるとき，① が最後に重なる三角形が ⑦ となる確率を求めなさい。
行き先が ➆ になるのは２通り，すべての組み合わせは８通りなので，
求める確率は，\( \dfrac{2}{8}=\dfrac{1}{4} \)
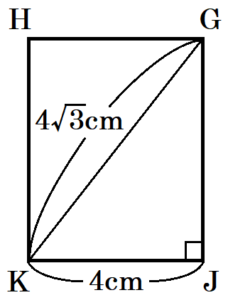
問２ 図３は，図１の二等辺三角形を底面とする三角柱で，\( GH=GI=4 \; cm \) としたものです。\( △GKL \) が正三角形であるとき，この三角柱の体積を求めなさい。
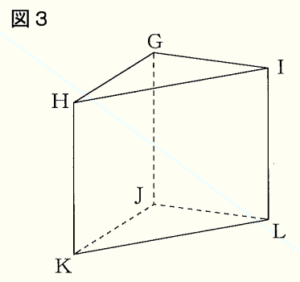
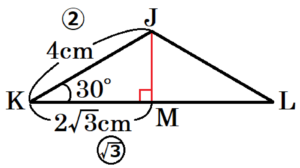
\( △GHI≡△JKL \) なので，点 \( J \) から辺 \( KL \) に垂線をひくと，
\( △JKM \) は \( 30°，60°，90° \) の直角三角形になっています。
ここから，
\( JM=\dfrac{1}{2}JK=2 \; (cm) \)
\( KM=\dfrac{\sqrt{3}}{2}JK=2\sqrt{3} \; (cm) \)
\( KL=2KM=4\sqrt{3} \; (cm) \)
であり，
\( △JKL=4\sqrt{3} \times 2 \times \dfrac{1}{2}=4\sqrt{3} \; (cm^2) \)
面 \( GHKJ \) に注目すると，
\( △GKL \) は正三角形なので，\( GK=KL=4\sqrt{3} \; cm \) であり，
三平方の定理より，
\( GJ^2=4\sqrt{3}^2-4^2=32 \)
\( GJ=4\sqrt{2} \; (cm) \)
よって，この三角柱の体積を \( V \; (cm^3) \) とすると，
\( V=4\sqrt{3} \times 4\sqrt{2}=16\sqrt{6} \; (cm^3) \)
