大問1
(1) 次のア~オを計算しなさい。
ア \( 4-(-1) \)
イ \( 8 \times (-3) \div 4 \)
【解説】
\( =\dfrac{8 \times (-3)}{4} \)
\( =2 \times (-3) \)
\( =-6 \)
ウ \( (9x-6y) \div \left( -\dfrac{3}{2} \right) \)
【解説】
\( =3(3x-2y) \times \left( -\dfrac{2}{3} \right) \)
\( =\dfrac{-6(3x-2y)}{3} \)
\( =-2(3x-2y) \)
\( =-6x+4y \)
エ \( \dfrac{2x+y-1}{3}-\dfrac{3x-2y+3}{5} \)
【解答】
\( \dfrac{x+11y-14}{15} \)
【解説】
\( =\dfrac{5(2x+y-1)}{15}-\dfrac{3(3x-2y+3)}{15} \)
\( =\dfrac{5(2x+y-1)-3(3x-2y+3)}{15} \)
\( =\dfrac{x+11y-14}{15} \)
オ \( (\sqrt{6}+\sqrt{2})(\sqrt{24}-\sqrt{8}) \)
【解説】
\( =(\sqrt{6}+\sqrt{2})(2\sqrt{6}-2\sqrt{2}) \)
\( =2(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2}) \)
\( =2(6-2) \)
\( =8 \)
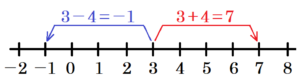
(2) 数直線上で,\( 3 \) からの距離が \( 4 \) である数を2つ書きなさい。
(3) 右の図のような同じ大きさのクリップが箱の中にたくさん入っている。\( 24 \) 個取り出して印をつけた後,すべて箱に戻してよくかき混ぜた。その中から \( 35 \) 個のクリップを無作為に取り出したところ,印のついたクリップは \( 2 \) 個であった。この結果から,箱の中にはおよそ何個のクリップが入っていると考えられるか,求めなさい。
【解説】
箱の中のクリップ全体の数:印をつけたクリップの数 \( = \) 取り出したクリップの数:取り出したクリップのうち印のついたクリップの数
となるので,
箱の中のクリップ全体の数を \( P \) とすると,
\( P:24=35:2 \)
\( 2P=840 \)
\( P=420 \)(個)
(4) 次の式を展開しなさい。
\( \left( \dfrac{1}{3}x+3 \right)^2 \)
【解答】
\( \dfrac{1}{9}x^2+2x+9 \)
【解説】
\( =\left( \dfrac{1}{3}x \right)^2+2 \times \dfrac{1}{3}x \times 3 +3^2 \)
\( =\dfrac{1}{9}x^2+2x+9 \)
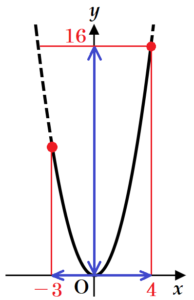
(5) 関数 \( y=x^2 \) について,\( x \) の変域が \( -3≦x≦a \) のとき,\( y \) の変域は \( b≦y≦16 \) である。このとき,\( a,b \) の値をそれぞれ求めなさい。
【解説】
\( y=16 \) となるときの \( x \) の値は
\( 16=x^2 \)
\( x=4 \) ( \( -3≦x \) より)
ここから,\( a=4 \)
関数 \( y=cx^2 \;\; (c>0) \) において,
\( x \) の変域が \( 0 \) を含むとき,
\( y \) の最小値は必ず \( 0 \) になるので,
\( b=0 \)
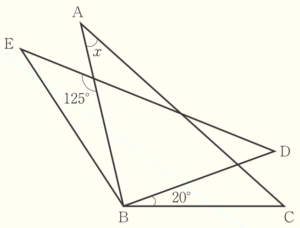
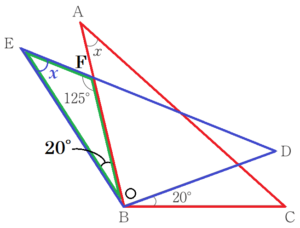
(6) 下の図で,\( △ABC≡△EBD \) である。このとき,\( ∠x \) の大きさを求めなさい。
【解説】
辺 \( AB \) と辺 \( DE \) の交点を点 \( F \) とすると,
\( △ABC≡△EBD \) より,
\( ∠ABC=∠EBD \) なので,
\( ∠FBD+∠DBC=∠FBD+∠EBF \)
\( ∠DBC=∠EBF \)
\( ∠DBC=20° \) より,\( ∠EBF=20° \)
\( △EBF \) において,
\( ∠BEF=180°-(125°+20°)=35° \)
\( △ABC≡△EBD \) より,
\( ∠BEF=∠BAC \) なので,
\( ∠x=∠BEF=35° \)
(7) 次のことがらは正しいが,その逆は正しくない。正しくないことを示すための反例を1つ書きなさい。
\( x=3,y=1 \) ならば,\( x+y=4 \) である。
【解説】
「Aならば,Bである」の逆は「Bならば,Aである」なので,
このことがらの逆は
\( x+y=4 \) ならば,\( x=3,y=1 \) である。
となります。
\( x+y=4 \) を満たす \( x,y \) の組み合わせは,\( x=2,y=2 \) など無数にあります。
(8) 方程式 \( 2x+y=3 \) について述べた文として適切でないものを,次のア~エの中から1つ選び,その記号を書きなさい。
ア この方程式では,\( x \) の値を1つ決めると,それに対応して \( y \) の値がただ1つに決まる。
イ この方程式を成り立たせる \( x,y \) の値の組は無数にある。
ウ この方程式のグラフは点 \( (1,1) \) を通る。
エ この方程式のグラフは点 \( (0,3) \) を通り,傾き \( 2 \) の直線と一致する。
【解説】
\( 2x+y=3 \) を \( y \) について解くと,\( y=-2x+3 \) となり,グラフは下の図のような直線になります。
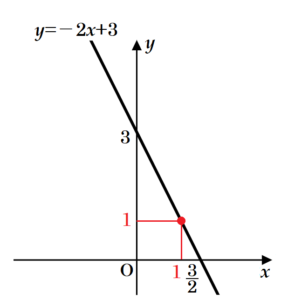
ア グラフは一次関数の直線になっているので,
\( x \) の値を1つ決めると,それに対応して \( y \) の値がただ1つに決まります。
イ この直線は無限に伸ばすことができるので,
この方程式を成り立たせる \( x,y \) の値の組も無数にあります。
ウ \( y=-2x+3 \) に \( x=1 \) を代入すると,\( y=-2 \times 1+3=1 \) となるので,
このグラフは点 \( (1,1) \) を通ります。
エ \( y=-2x+3 \) に \( x=0 \) を代入すると,\( y=-2 \times 0+3=3 \) となるので,
このグラフは点 \( (0,3) \) を通りますが,グラフの傾きは \( -2 \) になっています。
大問2
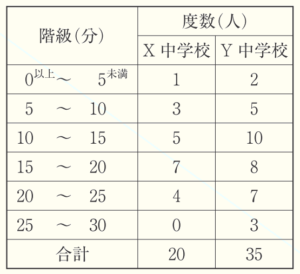
(1) 右の表は,X中学校とY中学校の生徒の通学時間を度数分布表に整理したものである。次のア,イに答えなさい。
ア Y中学校について,中央値がふくまれる階級を書きなさい。
【解答】
\( 15 \) 分以上 \( 20 \) 分未満
【解説】
Y中学校の生徒数は全体で \( 35 \) 人なので,
中央値になるのは,通学時間の短い方から \( 18 \) 番目の人の値になります。
通学時間が \( 15 \) 分未満の人の度数の合計は \( 2+5+10=17 \)(人)なので,
\( 18 \) 番目の人の値は,\( 15 \) 分以上 \( 20 \) 分未満の階級に含まれることになります。
イ この度数分布表から読み取れることとして適切なものを,次の1~4の中から1つ選び,その番号を書きなさい。
1 通学時間が \( 15 \) 分未満の生徒が,X中学校では4人いる。
2 通学時間の最大値は,X中学校の方がY中学校より大きい。
3 通学時間が \( 20 \) 分以上 \( 25 \) 分未満の階級の相対度数は,どちらの中学校も等しい。
4 通学時間が \( 20 \) 分未満の生徒の全体に対する割合は,X中学校の方がY中学校より小さい。
【解説】
1 X中学校で,通学時間が \( 15 \) 分未満の階級の度数は,\( 1+3+5=9 \)(人)になります。
2 X中学校の通学時間の最大値は \( 20 \) 分以上 \( 25 \) 分未満の階級に,
Y中学校の通学時間の最大値は \( 25 \) 分以上 \( 30 \) 分未満の階級に含まれているので,
通学時間の最大値は,Y中学校の方が大きい。
3 相対度数は,「その階級の度数」 \( \div \) 「すべての階級の度数の合計」で求めることができます。
X中学校の相対度数 \( =4 \div 20=0.2 \)
Y中学校の相対度数 \( =7 \div 35=0.2 \)
となり,両中学校の相対度数は等しい。
4 通学時間が \( 20 \) 分未満の生徒数は,
X中学校が \( 1+3+5+7=16 \)(人)なので,全体に対する割合は,\( 16 \div 20=0.8 \)
Y中学校が \( 2+5+10+8=25 \)(人)なので,全体に対する割合は,\( 25 \div 35=0.71・・・ \)
よって,X中学校の方が大きい。
(2) 下の【問題】とそれについて考えているレンさんとメイさんの会話を読んで,次のア,イに答えなさい。
【問題】
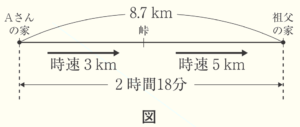
Aさんは,峠を越えて \( 8.7 \; km \) 離れた祖父の家に行くのに,Aさんの家から峠までは時速 \( 3 \; km \),峠から祖父の家までは時速 \( 5 \; km \) で歩いたら,合計 \( 2 \) 時間 \( 18 \) 分かかった。Aさんの家から峠までの道のりと,峠から祖父の家までの道のりはそれぞれ何 \( km \) か,求めなさい。
レン:【問題】にある数量の関係を図に表してみたよ。 ただ,求めたい道のりの他に,歩いたそれぞれの時間もわからないね。
メイ:それなら,表にして整理してみよう。求めたい道のりは2つだから,それぞれ \( x,y \) と文字にしたらどうかな。

レン:道のりについて,\( x,y \) を用いた方程式がつくれるね。
メイ:そうだね。その他に,もう1つ方程式をつくれるよ。
ア あ , い にあてはまる式をそれぞれ書きなさい。また, う にあてはまる数を書きなさい。
【解答】
あ ・・・ \( \dfrac{x}{3} \)
い ・・・ \( \dfrac{y}{5} \)
う ・・・ \( 2.3 \)
【解説】
う
\( 18 \) 分を時間に換算すると,\( \dfrac{18}{60}=\dfrac{3}{10}=0.3 \)(時間)なので,
\( 2 \) 時間 \( 18 \) 分 \( =2+0.3=2.3 \) (時間)になります。
イ 【問題】を解きなさい。
【解答】
家から峠までの道のり ・・・ \( 4.2 \; km \)
峠から祖父の家までの道のり ・・・ \( 4.5 \; km \)
【解説】
\( \left\{ \begin{array}{}
x+y=8.7 \;\; ・・・ \;\; ➀ \\
\dfrac{x}{3}+\dfrac{y}{5}=2.3 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀\( \times 10 \;\; – \) ➁\( \times 30 \)
\( 4y=18 \)
\( y=4.5 \)
➀に代入すると,
\( x+4.5=8.7 \)
\( x=4.2 \)
大問3
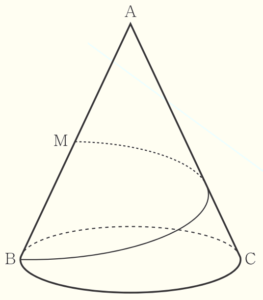
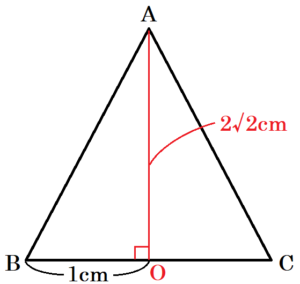
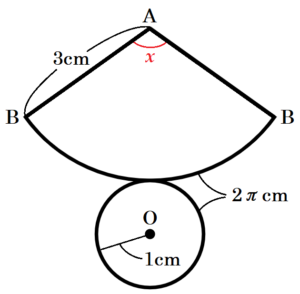
(1) 右の図は,底面の半径が \( 1 \; cm \),高さが \( 2\sqrt{2} \; cm \) の円錐である。母線 \( AB \) の中点をMとし,点 \( B \) から点 M まで,円錐の側面にそって母線 AC を通り,最も短くなるように糸をかける。次のア~ウに答えなさい。
ア 母線 \( AB \) の長さを求めなさい。
【解説】
点 \( A \) から底面に垂線をひき,交点を点 \( O \) とすると,
\( △ABO \) において,三平方の定理より,
\( AB^2=(2\sqrt{2})^2+1^2=9 \)
\( AB=3 \; (cm) \) ( \( AB>0 \) より)
イ この円錐の展開図をかいたとき,側面になるおうぎ形の中心角の大きさを求めなさい。
【解説】
この円錐を母線 \( AB \) で切って展開すると,
右の図のようになります。
底面の円の円周と側面のおうぎ形の弧の長さは
等しいので,
\( 2 \pi{} \times 1=2 \pi{} \; (cm) \)
側面になるおうぎ形の中心角を \( x° \) とし,
おうぎ形の弧の長さについて方程式をたてると,
\( 2 \pi{} \times 3 \times \dfrac{x}{360}=2 \pi{} \)
\( 3x=360 \)
\( x=120 \)
ウ 糸の長さを求めなさい。
【解答】
\( \dfrac{3\sqrt{7}}{2} \; cm \)
【解説】
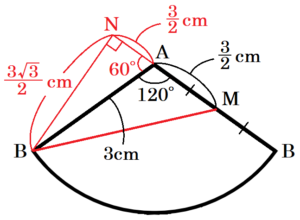
糸をかけた状態でこの円すいを展開すると,
側面のおうぎ形に対して,糸は右の図の \( BM \) になります。
図のように線分 \( AB \) を延長し,もう一方の点 \( B \)
から垂線をひいた交点を点 \( N \) とすると,
\( △ABN \) は \( 30°,60°,90° \) の直角三角形なので, \( AB=3 \; cm \) より,
\( AN=\dfrac{1}{2}AB=\dfrac{3}{2} \; (cm) \)
\( BN=\dfrac{\sqrt{3}}{2}AB=\dfrac{3\sqrt{3}}{2} \; (cm) \)
\( △BMN \) において,三平方の定理より,
\( BM^2=\left( \dfrac{3\sqrt{3}}{2} \right)^2+3^2=\dfrac{63}{4} \)
\( BM=\dfrac{3\sqrt{7}}{2} \; (cm) \) ( \( BM>0 \) より)
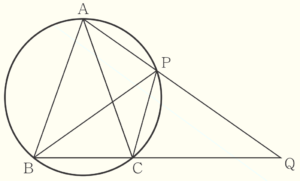
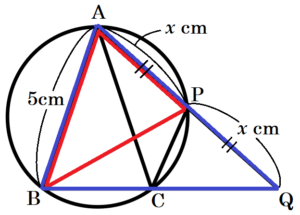
(2) 下の図のように,3点 \( A,B,C \) を通る円があり,\( △ABC \) は \( AB=AC=5 \; cm \) の二等辺三角形である。点 \( P \) は点 \( B \) をふくまない弧 \( AC \) 上を動く点であり,直線 \( AP \) と直線 \( BC \) の交点を \( Q \) とする。このとき,次のア,イに答えなさい。
ア \( △ABP \) と \( △AQB \) が相似になることを次のように証明した。 あ ~ う にあてはまる角をそれぞれ書きなさい。
[証明]
\( △ABP \) と \( △AQB \) において
共通な角だから
\( ∠BAP=∠QAB \) ・・・ ➀
\( △ABC \) は二等辺三角形だから
\( ∠ABC= \)
あ ・・・ ➁
円周角の定理より
あ \( = \)
い ・・・ ➂
②,③から
い \( = \)
う ・・・ ➃
➀,④から
2組の角がそれぞれ等しいので
\( △ABP \) ∽ \( △AQB \)
【解答】
あ ・・・ \( ∠ACB \)
い ・・・ \( ∠APB \)
う ・・・ \( ∠ABQ \)
イ 点 \( P \) が線分 \( AQ \) の中点になるとき, 線分 \( AP \) の長さを求めなさい。
【解答】
\( \dfrac{5\sqrt{2}}{2} \; cm \)
【解説】
ア より,\( △ABP \) ∽ \( △AQB \) なので,
\( AP=x \; cm \) とすると,
\( AP:AB=AB:AQ \)
\( x:5=5:2x \)
\( 2x^2=25 \)
\( x^2=\dfrac{25}{2} \)
\( x=\dfrac{5\sqrt{2}}{2} \; (cm) \) ( \( x>0 \) より)
大問4
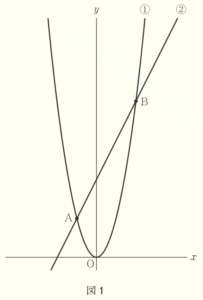
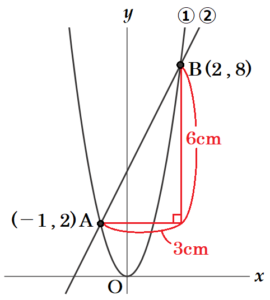
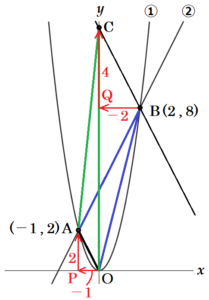
図1で,①は関数 \( y=2x^2 \) のグラフであり,2点 \( A,B \) は①上の点で \( x \) 座標がそれぞれ \( -1,2 \) である。また,②は2点 \( A,B \) を通る直線である。次の(1)~(3)に答えなさい。ただし,座標軸の単位の長さを \( 1 \; cm \) とする。
(1) 点 \( A \) の \( y \) 座標を求めなさい。
【解説】
点 \( A \) は \( y=2x^2 \) 上の点で,
\( x \) 座標が \( -1 \) なので,
\( y=2 \times (-1)^2=2 \)
(2) 線分 \( AB \) の長さを求めなさい。
【解答】
\( 3\sqrt{5} \; cm \)
【解説】
点 \( B \) は \( y=2x^2 \) 上の点で,
\( x \) 座標が \( 2 \) なので,
\( y=2 \times 2^2=8 \)
よって,\( A(-1,2),B(2,8) \) 間の距離は,
\( AB^2=\{2-(-1)\}^2+(8-2)^2=45 \)
\( AB=3\sqrt{5} \; (cm) \) ( \( AB>0 \) より)
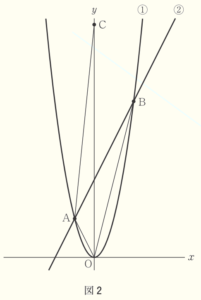
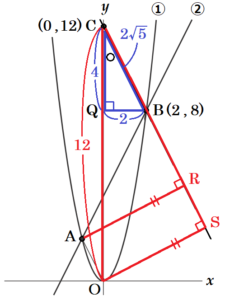
(3) 図2は,図1に面積の等しい \( △AOB \) と \( △AOC \) をかき加えたものである。点 \( C \) は \( y \) 軸上の点で,\( y \) 座標が正であるとき,次のア,イに答えなさい。
ア 点 \( C \) の座標を求めなさい。
【解説】
\( △AOB \) と \( △AOC \) は辺 \( OA \) が共通で
面積が等しいことから,等積変形の考え方により
\( OA//BC \) になっています。
点 \( A \) から \( x \) 軸に垂線をひいた交点を点 \( P \),
点 \( B \) から \( y \) 軸に垂線をひいた交点を点 \( Q \)
とすると,\( △APO \) ∽ \( △CQB \) となっています。
このとき,点 \( O \) から見て,点 \( A \) は,
\( x \) 方向に \( -1 \),\( y \) 方向に \( 2 \) 進んだ位置にあるので,
点 \( B \) から見て,点 \( C \) は,
\( x \) 方向に \( -2 \) 進んだ位置にあることから,
\( y \) 方向に \( 4 \) 進んだ位置にあることになります。
よって,
点 \( C \) の \( y \) 座標は \( 8+4=12 \) になります。
イ 点 \( A \) と2点 \( B,C \) を通る直線との距離を求めなさい。
【解答】
\( \dfrac{12\sqrt{5}}{5} \; cm \)
【解説】
点 \( A,O \) から直線 \( BC \) に垂線をひいた交点をそれぞれ点 \( R,S \) とすると,
求める距離は線分 \( AR \) の長さと等しくなります。
また,\( OA//BC \) より,\( OS=AR \) になっているので,\( OS \) の長さを求めることにします。
\( △CSO \) と \( △CQB \) に注目すると,
\( ∠C \) が共通
\( ∠CSO=∠CQB=90° \)
より,
\( △CSO \) ∽ \( △CQB \) となっています。
\( △CQB \) において,
\( BQ=2 \; cm,CQ=4 \; cm \) より,
\( BC=2\sqrt{5} \; cm \) なので,
\( BC:OC=BQ:OS \)
\( 2\sqrt{5}:12=2:OS \)
\( 2\sqrt{5}OS=24 \)
\( OS=\dfrac{12\sqrt{5}}{5} \; (cm) \)
大問5
下の【自由研究】 は,マユさんが冬休みの課題として提出したものの一部である。次の(1),(2)に答えなさい。

(1) 【自由研究】「3 結果」 の ① について,次のア,イに答えなさい。
ア あ にあてはまる数を書きなさい。
【解説】
下の図のとおり,5本になります。
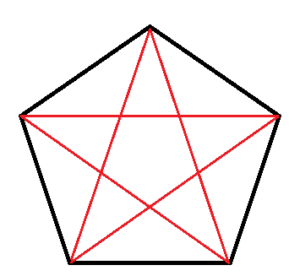
イ い に適切な内容を書きなさい。
【解答】
\( 1 \) 本の対角線を2回ずつ重複して数える
【解説】
例として正五角形 \( n=5 \) の場合を考えます。
1つの頂点から \( 5-3=2 \)(本)ずつ対角線をひくことになり,
これを5つの頂点から素直に数えると,
対角線 \( AC \) の場合,頂点 \( A \) から引いた場合と
頂点 \( C \) から引いた場合の2回数えることになります 。
これが,すべての対角線について言えるので,
\( 2 \) で割って半分にする必要があります。
(2) 【自由研究】「3 結果」の② について,次のア,イに答えなさい。
ア う にあてはまる数を書きなさい。また, え にあてはまる式を書きなさい。
【解答】
う ・・・ \( 15 \)
え ・・・ \( n(n-1) \)
【解説】
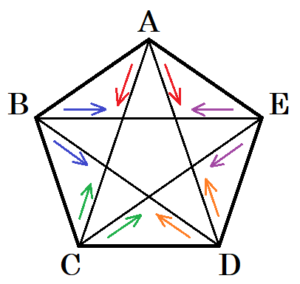
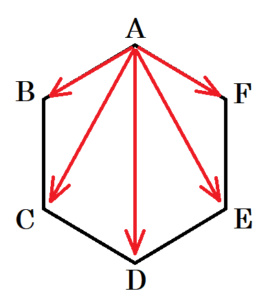
6人の選手が他の選手全員と1回ずつ試合をするとき,下の図のように,選手Aは対角線でつないだ選手C,D,Eの他に,辺でつないだ選手B,Fとも試合をするので
\( \dfrac{5 \times 6}{2}=15 \)(試合)
イ 試合数が \( 66 \) 試合のとき,選手の人数を求めなさい。
【解説】
試合数が \( 66 \) 試合のとき,
\( \dfrac{n(n-1)}{2}=66 \)
\( n(n-1)=132 \)
\( n^2-n-132=0 \)
\( (n+11)(n-12)=0 \)
\( n=12 \) ( \( n>0 \) より)