大問１
問１ \( 5+3 \times (-4) \) を計算しなさい。
問２ \( (2\sqrt{3}-\sqrt{7})(2\sqrt{3}+\sqrt{7}) \) を計算しなさい。
問３ 比例式 \( x：(x-3)=5：3 \) で，\( x \) の値を求めなさい。
問４ 連立方程式 \( \left\{ \begin{array}{}
2x+3y=1 \\
x-y=3 \\
\end{array} \right. \) を解きなさい。
問５ 方程式 \( (x-2)^2=7 \) を解きなさい。
問６ 次の１，２にある数量の関係を，等式か不等式で表しなさい。
１ \( 20 \; L \) 入る容器に毎分 \( x \; L \) ずつ水を入れるとき，容器が水でいっぱいになるまで \( y \) 分間かかる。
２ \( 30 \; m \) のテープから \( a \; m \) のテープを \( 5 \) 本切り取ると，残りは \( b \; m \) より長い。
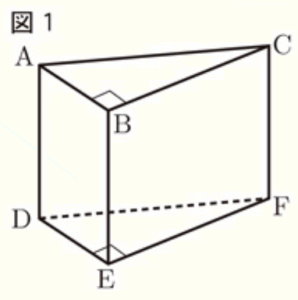
問７ 図１は，底面が直角三角形で，側面がすべて長方形の三角柱である。平面 \( ADEB \) と垂直な平面を，後のア~エからすべて選び，記号で答えなさい。
ア 平面 \( ABC \)
イ 平面 \( DEF \)
ウ 平面 \( ADFC \)
エ 平面 \( BEFC \)
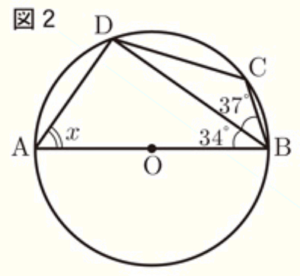
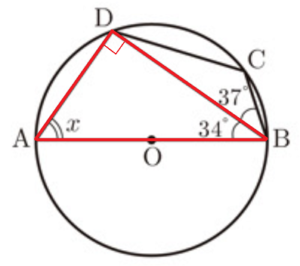
問８ 図２のように，円 \( O \) の円周上に４点 \( A，B，C，D \) をとる。\( AB \) が直径であるとき，\( ∠x \) の大きさを求めなさい。
直径 \( AB \) の円周角なので，\( ∠ADB=90° \)
\( △ABD \) において，
\( ∠x=180°-(90°+34°)=56° \)
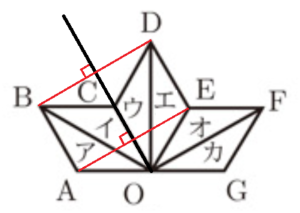
問９ 太郎さんは，近所のお店に飾られている組子とよばれる木工細工を見た。組子の模様の１つに，図３のような二等辺三角形を組み合わせてできている「麻の葉」とよばれるものがあった。太郎さんはその美しさに感動し，図４のように組子の模様の一部を作図した。二等辺三角形をそれぞれア～カとすると，ア～カはすべて合同である。後の１，２に答えなさい。
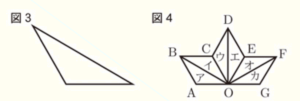
１ 三角形アを，直線 \( OC \) を対称の軸として，対称移動して重ね合わせることができる三角形を，イ～カから１つ選び，記号で答えなさい。
ある図形をある直線を軸として対象移動したとき，
移動前の点と移動後の点を結んだ線分は，
対称の軸と垂直に交わります。
点 \( A，B \) から直線 \( OC \) に垂線をひき延長すると，
点 \( E，D \) を通ります。
よって，移動後の図形は「エ」になります。
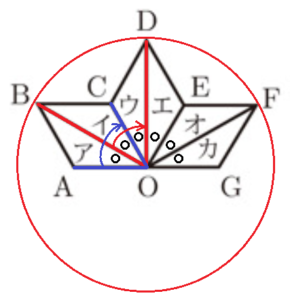
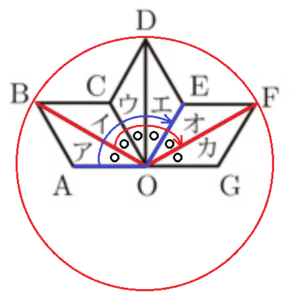
２ 三角形アを，点 \( O \) を回転の中心として，回転移動して重ね合わせることができる三角形を，イ～カからすべて選び，記号で答えなさい。
移動前の点と移動後の点は，同一円周上の点になります。
点 \( O \) を中心とした円で，
点 \( B \) と同一円周上にある点は，点 \( D，F \) になります。
点 \( A \) と同一円周上にある点は，点 \( C，E，G \) になります。
ア～カはすべて合同な二等辺三角形なので，
線分 \( OB \) を 線分 \( OD \) に重なるまで回転させたとき，
底角２個分回転したことになります。
線分 \( OA \) を底角２個分回転すると，線分 \( OC \) に重なります。
ここから，移動後の三角形は「ウ」になります。
線分 \( OB \) を 線分 \( OF \) に重なるまで回転させたとき，
底角４個分回転したことになります。
線分 \( OA \) を底角４個分回転すると，線分 \( OE \) に重なります。
ここから，移動後の三角形は「オ」になります。
大問２
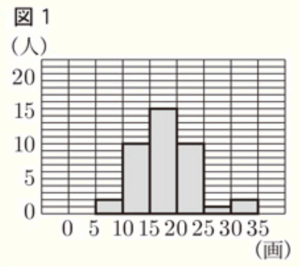
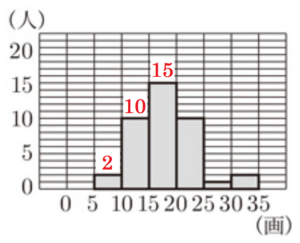
問１ 太郎さんは，生徒の名前の画数を「花子」であれば \( 10 \) 画，「クリス」 であれば \( 6 \) 画のように調べた。図１は，太郎さんの学校の２０２３年度の３年生 \( 40 \) 人について，調べた結果をヒストグラムに表したものである。 例えば，\( 30 \) 画以上 \( 35 \) 画未満の階級の度数は \( 2 \) 人である。後の１，２に答えなさい。
１ 最初の階級から \( 15 \) 画以上 \( 20 \) 画未満の階級までの累積度数を求めなさい。
ヒストグラムから，
\( 5 \) 画以上 \( 10 \) 画未満の階級の度数は \( 2 \) 人，
\( 10 \) 画以上 \( 15 \) 画未満の階級の度数は \( 10 \) 人，
\( 15 \) 画以上 \( 20 \) 画未満の階級の度数は \( 15 \) 人
なので，累積度数は，
\( 2+10+15=27 \)（人）
２ 図２は２０２３年度，２０１８年度，２０１３年度，２００８年度の３年生について，調べた結果を箱ひげ図に表したものである。ただし，３年生の人数は年度によって異なる場合がある。後の（１），（２）に答えなさい。
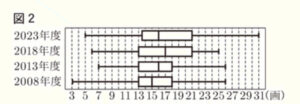
（１） 図２の箱ひげ図から読みとれることとして正しいと判断できるものを，次のア～オから２つ選び，記号で答えなさい。
ア ２０２３年度と２０１８年度の第１四分位数は等しい。
イ ２０２３年度と２０１３年度では，範囲も四分位範囲も２０２３年度の方が大きい。
ウ ２０１８年度の平均値は \( 17 \) 画である。
エ ２０１３年度には \( 10 \) 画以下の人はいない。
オ どの年度も半数以上の人が \( 15 \) 画以上である。
ア ２０２３年度の第１四分位数は，約 \( 13.5 \) 画，２０１８年度の第１四分位数は，\( 13 \) 画
なので，正しくない。
イ 範囲 ･･･ ２０２３年度が \( 31-5=26 \) 画，２０１３年度が \( 26-7=19 \) 画
四分位範囲 ･･･ ２０２３年度が \( 21-13.5=7.5 \) 画，２０１３年度が \( 18-13=5 \) 画
なので，正しい。
ウ 箱ひげ図のデータだけでは平均値はわからないので，正しくない。
エ 最小値が \( 7 \) 画であることから，\( 7 \) 画の人がいるので，正しくない。
オ 中央値が最も小さいのは２０１３年度で，\( 15 \) 画なので，正しい。
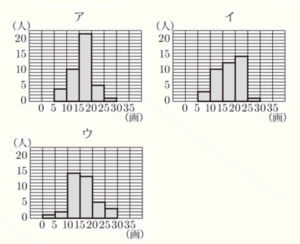
（２） 次のア～ウは，２０１８年度，２０１３年度，２００８年度のいずれかのデータを使って作成したヒストグラムであり，図２の箱ひげ図と対応している。２０１３年度のヒストグラムを，次のア～ウから１つ選び，記号で答えなさい。
問２ 太郎さんは，祭りでかき氷を販売することにした。販売した個数を \( x \) 個，販売額の合計を \( y \) 円とし，\( y \) を \( x \) の関数とみなして，\( x \) と \( y \) の関係について調べた。 次の１，２に答えなさい。ただし，消費税は考えないものとする。
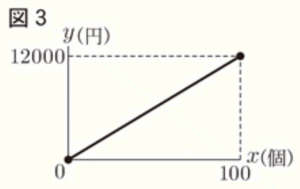
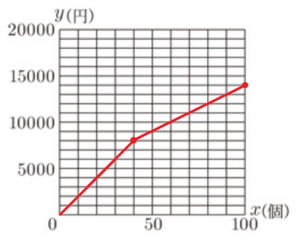
１ 図３は，かき氷１００個をすべて同じ価格で販売したときのグラフである。１個の価格を求めなさい。
２ 太郎さんは，かき氷を \( 100 \) 個販売することにした。売れ行きによっては，途中で値下げして残りすべてを販売するつもりである。次の（１）～（３）に答えなさい。
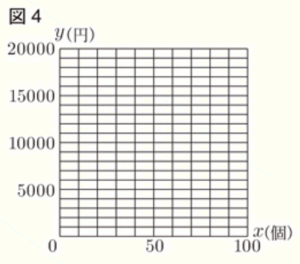
（１） はじめのうちは１個の価格を \( 200 \) 円にして \( 40 \) 個販売し，その後，１個の価格を \( 100 \) 円に値下げして残りすべてを販売したときの \( x \) と \( y \) の関係を表すグラフを図４にかきなさい。
（２） （１）の販売額の合計は，１個の価格を \( 200 \) 円にして \( 100 \) 個すべてを販売した場合と比べていくら少なくなるか， 求めなさい。
（３） はじめのうちは１個の価格を \( 200 \) 円にして何個か販売し，その後，１個の価格を \( 100 \) 円に値下げして残りすべてを販売する。販売額の合計を \( 12000 \) 円以上にするためには，１個の価格を \( 200 \) 円にしているときに，何個以上販売する必要があるか，求めなさい。
大問３
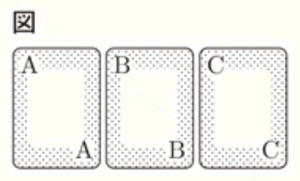
図のようにＡ，Ｂ，Ｃと書かれた３枚のカードがある。太郎さんと花子さんは，次のルールでゲームをくり返して行うことにした。後の問１，問２に答えなさい。
・ 花子さんは，異なる３つの自然数を決めて，小さい方から順にＡ，Ｂ，Ｃのカードに書く。
・ 花子さんは，３枚のカードをよく混ぜ，太郎さんに１枚ひいてもらう。
・ ひいた１枚のカードに書かれた数の２乗した数を，太郎さんの得点とする。
・ 残った２枚のカードに書かれた２つの数の積を，花子さんの得点とする。
・ 太郎さんと花子さんの得点を比べ，大きい方を勝ちとする。ただし，得点が同じときは
引き分けとする。
問１ 太郎さんのカードのひき方は同様に確からしいものとする。次の１～３に答えなさい。
１ 太郎さんが３枚のカードから１枚ひくとき，Ａのカードをひく確率を求めなさい。
２ 次の（１），（２）に答えなさい。
（１） カードに書かれた数が，Ａは \( 1 \)，Ｂは \( 2 \)，Ｃは \( 3 \) のとき，太郎さんが勝つ確率を求めなさい。
（２） カードに書かれた数が，Ａは \( 1 \)，Ｂは \( 2 \)，Ｃは \( 4 \) のとき，花子さんが勝つ確率を求めなさい。
３ 太郎さんが勝つことの起こりやすさと，花子さんが勝つことの起こりやすさとが同じになるような，カードに書かれた３つの自然数の組を１組答えなさい。ただし，２の問題文中に出てきた数の組 \( (1，2，3)，(1，2，4) \) 以外の組を答えること。
問２ 太郎さんがＢのカードをひいたときの２人の得点について，次の文章を読んで，後の１，２に答えなさい。
例えば，カードに書かれた数が３つの連続する自然数のとき，太郎さんと花子さんの得点は，次の表１のようになる。
表１から，次のように予想することができる。
カードに書かれた数が３つの連続する自然数ならば，太郎さんがＢのカードをひいたとき，太郎さんの
得点は，花子さんの得点よりいつでも \( 1 \) 大きい。
予想１が正しいことは，次のように証明できる。
証明１
カードに書かれた３つの連続する自然数のうち，Ｂのカードに書かれた数を \( n \) とすると，Ａは \( n-1 \)，Ｃは \( n+1 \) と表すことができる。太郎さんがＢのカードをひいたとき，太郎さんの得点から花子さんの得点をひくと，
\( n^2-(n-1)(n+1)=n^2-(n^2-1) \)
\( = n^2-n^2+1 \)
\( =1 \)
したがって，カードに書かれた数が３つの連続する自然数ならば，太郎さんがＢのカードをひいたとき，太郎さんの得点は，花子さんの得点よりいつでも \( 1 \) 大きい。
カードに書かれた数が \( a \) ずつはなれた自然数のとき，太郎さんと花子さんの得点は，次の表２，表３のようになる。 ただし，\( a \) は自然数とする。
１ カードに書かれた数が \( a \) ずつはなれた自然数のとき，どんな性質があるかを次のように予想した。
ア にあてはまる数または式を入れ，予想２を完成しなさい。
カードに書かれた数が \( a \) ずつはなれた自然数ならば，太郎さんがＢのカードをひいたとき，太郎さんの得点は，花子さんの得点よりいつでも ア 大きい。
２ 予想２が正しいことを次のように証明した。 イ ， ウ にあてはまる数または式を入れなさい。
また， エ に証明の続きを書き入れ，証明２を完成しなさい。ただし， ア には１と同じものが入る。
証明２
カードに書かれた \( a \) ずつはなれた自然数のうち，Ｂのカードに書かれた数を \( n \) とすると，Ａは イ ，Ｃは ウ と表すことができる。太郎さんがＢのカードをひいたとき，太郎さんの得点から花子さんの得点をひくと，
エ
したがって，カードに書かれた数が \( a \) ずつはなれた自然数ならば，太郎さんがＢのカードをひいたとき，太郎さんの得点は，花子さんの得点よりいつでも ア 大きい。
大問４
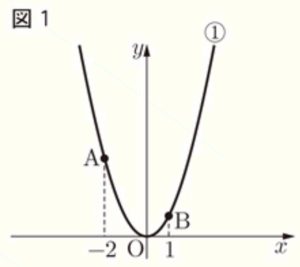
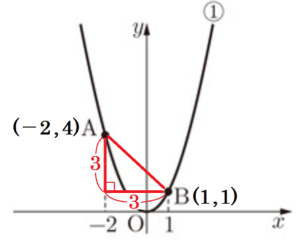
図１のように，関数 \( y=x^2 \) ･･･ ① のグラフ上に，２点 \( A，B \) があり，\( x \) 座標はそれぞれ \( -2，1 \) である。後の問１～問３に答えなさい。
問１ 次の１～３に答えなさい。
１ 点 \( A \) の \( y \) 座標を求めなさい。
２ ２点 \( A，B \) の間の距離を求めなさい。
２点 \( A，B \) の座標は \( A(-2，4)，B(1，1) \) なので，
\( AB^2=\{1-(-2)\}^2+(4-1)^2=18 \)
\( AB=3\sqrt{2} \)
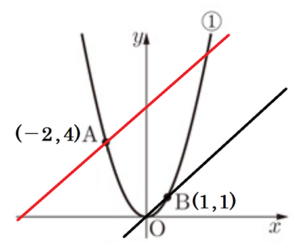
３ 直線 \( OB \) と傾きが等しく，点 \( A \) を通る直線の式を求めなさい。
直線 \( OB \) は \( O(0，0)，B(1，1) \) を通るので，
傾きは \( 1 \) になっています。
求める直線の式を \( y=x+b \) とすると，\( A(-2，4) \) を通るので，
\( 4=-2+b \)
\( b=6 \)
よって，求める直線の式は，\( y=x+6 \)
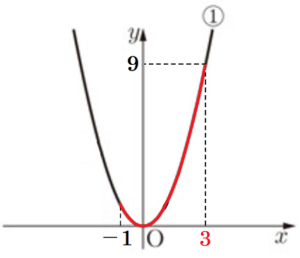
問２ 次の ア ， イ にあてはまる数をそれぞれ求めなさい。
\( y=x^2 \) において，\( y \) の値が \( 9 \) になるのは，
\( 9=x^2 \)
\( x=±3 \)
\( x \) の変域が \( -1≦x≦ \) ア であることから，
あてはまるのは \( x=3 \) のとき。
よって，\( x \) の変域は，\( -1≦x≦3 \)
\( x \) の変域が \( 0 \) を含んでいるので，最小値は \( 0 \)。
よって，\( x \) の変域は，\( 0≦y≦9 \)
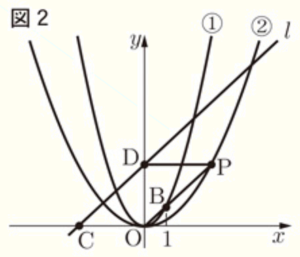
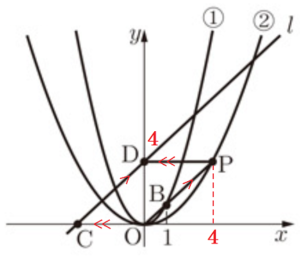
問３ 図２の直線 \( l \) は，関数 \( y=x+4 \) のグラフである。直線 \( l \) と \( x \) 軸の交点を \( C \)，直線 \( l \) と \( y \) 軸の交点を \( D \) とする。線分 \( OB \) を延長した直線上に，四角形 \( DCOP \) が平行四辺形となるような点 \( P \) をとる。ただし，点 \( P \) の \( x \) 座標は正とする。また，関数 \( y=ax^2 \) ( \( a \) は定数) ･･･② のグラフは，点 \( P \) を通る。後の１，２に答えなさい。
１ \( a \) の値を求めなさい。
四角形 \( DCOP \) が平行四辺形であることから，
直線 \( l//OP \) なので，直線 \( OP \) の傾きは \( 1 \) です。
ここから，直線 \( OP \) の式は \( y=x \) です。
直線 \( l \) の式は \( y=x+4 \) なので，
点 \( D \) の \( y \) 座標は \( 4 \) です。
四角形 \( DCOP \) が平行四辺形であることから，
\( CO//DP \) であり，
点 \( D \) と点 \( P \) の \( y \) 座標は等しいので，
点 \( P \) の \( y \) 座標も \( 4 \) です。
ここから，点 \( P \) の \( x \) 座標も \( 4 \) です 。
点 \( P(4,4) \) は，\( y=ax^2 \) 上の点なので，
\( 4=a \times 4^2 \)
\( a=\dfrac{1}{4} \)
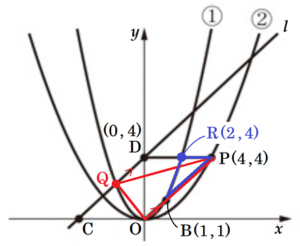
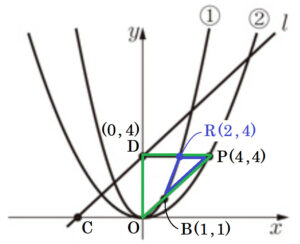
２ 関数 ② のグラフと辺 \( CD \) の交点を \( Q \) とする。また，関数 ① のグラフと辺 \( DP \) の交点を \( R \) とする。\( △OPQ \) と \( △BPR \) の面積の比を，最も簡単な整数の比で表しなさい。
\( l//OP \) より，等積変形の考え方から
\( △OPQ=△OPD \)なので，
\( △OPD \) と \( △BPR \) の面積の比を求めます。
点 \( R \) は \( y=x^2 \) 上の点で，
\( y \) 座標は \( 4 \) なので，
\( 4=x^2 \)
\( x=2 \) (\( R \) の \( x \) 座標は正のため)
ここから，\( R(2,4) \)
\( D(0,4)，P(4,4) \) より，
\( PD \) を底辺と考えると，\( △OPD \) の面積は，
\( △OPD=4 \times 4 \times \dfrac{1}{2}=8 \)
\( B(1,1)，P(4,4)，R(2,4) \) より，
\( PR \) を底辺と考えると，\( △BPR \) の面積は，
\( △BPR=2 \times 3 \times \dfrac{1}{2}=3 \)
よって，
\( △OPQ：△BPR=△OPD：△BPR=8：3 \)
大問５
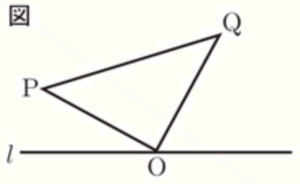
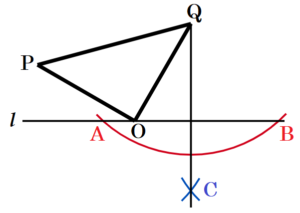
図１のように，直角二等辺三角形の三角定規を直線 \( l \) 上におき，三角定規の頂点がある位置を \( O，A，B \) とする。このとき，\( ∠AOB=90°，OA=OB \) である。この三角定規を，点 \( O \) を回転の中心として時計回りに回転させたとき，移動後の頂点を，図２のように \( P，Q \) とする。後の問１～問３に答えなさい。
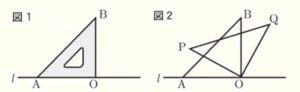
問１ \( ∠OPQ \) の大きさを求めなさい。
問２ 次の１，２に答えなさい。
１ 点 \( Q \) を通る直線 \( l \) の垂線を，コンパスと定規を用いて右の図に作図しなさい。ただし，作図に用いた線は消さないでおくこと。
手順１ 点 \( Q \) を中心に円弧を描く。
(直線 \( l \) との交点を点 \( A，B \) とします。)
手順２ ２点 \( A，B \) を中心に円弧を描く。
(交点を点 \( C \) とします。)
手順３ ２点 \( Q，C \) を通る直線を描く。
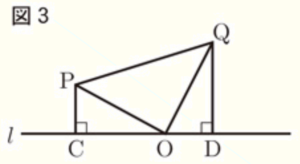
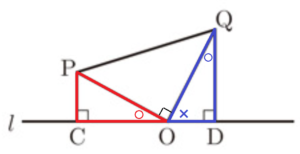
２ 図３のように，点 \( P，Q \) をそれぞれ通る直線 \( l \) の垂線をひき，直線 \( l \) との交点を順に \( C，D \) とする。\( △PCO≡△ODQ \) であることを証明しなさい。
\( △PCO \) と \( △ODQ \) において，
仮定より，
\( OP=QO \) ･･･ ➀
\( ∠PCO=∠ODQ=90° \) ･･･ ➁
３点 \( C，O，D \) は一直線上の点で，
\( ∠POQ=90° \) なので，
\( ∠COP=180°-(90°+∠DOQ) \)
\( =90°-∠DOQ \) ･･･ ➂
三角形の内角の和は \( 180° \) なので，
\( ∠DQO=180°-(90°+∠DOQ) \)
\( =90°-∠DOQ \) ･･･ ➃
③➃より，
\( ∠COP=∠DQO \) ･･･ ➄
➀➁➄より，
直角三角形の斜辺と他の１つの鋭角がそれぞれ等しいので，
\( △PCO≡△ODQ \)
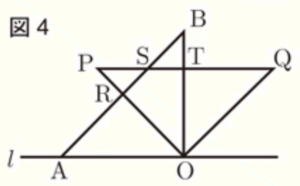
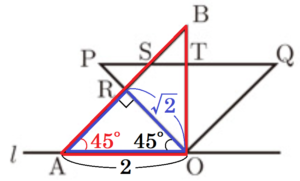
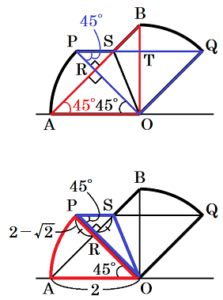
問３ 図４は \( ∠AOP=45° \) となるまで三角定規を回転したものである。辺 \( OP \) と辺 \( AB \) の交点を \( R \)，辺 \( PQ \) と辺 AB の交点を \( S \)，辺 \( PQ \) と辺 \( OB \) の交点を \( T \) とする。\( OA=2 \) のとき，後の１，２に答えなさい。
１ \( PR \) の長さを求めなさい。
\( △AOR \) において，
\( △AOB \) は直角二等辺三角形なので，
\( ∠OAR=∠OAB=45° \) ･･･ ➀
\( ∠AOP=45° \) なので，
\( △AOR \) は直角二等辺三角形であり，
\( OR：OA=1：\sqrt{2} \)
\( OR：2=1：\sqrt{2} \)
\( \sqrt{2}OR=2 \)
\( OR=\sqrt{2} \)
\( OP=OA=2 \) なので，
\( PR=OP-OR=2-\sqrt{2} \)
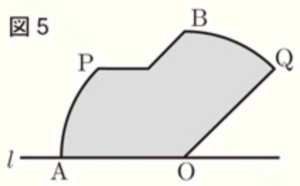
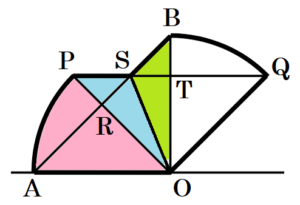
２ 図５の色をつけて表した部分は，\( ∠AOP=45° \) となるまで三角定規を回転したときに，三角定規が通った部分である。色をつけて表した部分の面積を求めなさい。
図形 \( OAPS \) と図形 \( OQBS \) が直線 \( OS \) に対して対称な図形であることに注目すると，
右の図のとおり図形 \( OAPS \) は，おうぎ形 \( OAP \) と \( △OPS \) をくっつけた形になっています。
【おうぎ形 \( OAP \) の面積】
\( \pi{} \times 2^2 \times \dfrac{45}{360}=\dfrac{1}{2}\pi{} \)
【\( △OPS \) の面積】
１より，\( ∠ARO=90° \) であることから，
対頂角は等しいので，\( ∠PRS=90° \)
さらに，\( ∠RPS=45° \) なので，
\( △PRS \) は直角二等辺三角形であり，
\( SR=RP=2-\sqrt{2} \)
よって，
\( OP \times SR \times \dfrac{1}{2}=2 \times (2-\sqrt{2}) \times \dfrac{1}{2} \)
\( =2-\sqrt{2} \)
図形 \( OAPS \) の面積は，\( 2-\sqrt{2}+\dfrac{1}{2}\pi{} \)
部分の面積は，図形 \( OAPS \) ２個分なので，
\( 2 \times \left(\dfrac{1}{2}\pi{}+2-\sqrt{2} \right)=\pi{}+4-2\sqrt{2} \)
