指数を含む計算
指数を使った数の表し方
同じ数を何個かかけたものを 累乗 といい,
2個かけたときは 2乗(または 平方 ) → 面積を表す単位「平方メートル \( (m^2) \)」の平方です。
3個かけたときは 3乗(または 立方 ) → 体積を表す単位「立方メートル \( (m^3) \)」の立方です。
4個かけたときは 4乗
・・・
と呼びます。
例えば,\( 2 \) を3個かけた数は \( 2 \) の右上に小さく \( 3 \) と書いて
\( 2 \times 2 \times 2=\large{2^3} \)
と表し,「2の3乗」と読みます。
このとき,右上に小さく書いた数を 指数 といいます。
指数を使って数を表すときの注意点
「 - 」の符号がつく場合の注意点
指数を使って表される数について「 - 」の符号がつく場合には注意が必要で,
負の数の累乗を表す場合には必ずかっこをつける 必要があります。
例 \( -3^2 \) と \( (-3)^2 \) の違い
\( -3^2 \) は, \( 3 \) を2個かけた数に「-」の符号をつけた数
\( -3^2=-(3 \times 3)=-9 \)
\( (-3)^2 \) は, \( -3 \) を2個かけた数
\( (-3)^2=-3 \times (-3)=9 \)
と,どちらも「ー3の2乗」と読めてしまいますが,異なる数を表しています。
分数の累乗の表し方
「 - 」の符号がつく場合以外に分数の累乗を表す場合にも注意が必要です。
分数の累乗を表す場合にも必ずかっこをつける 必要があります。
例 \( \dfrac{\;3^2}{2} \) と \( \left( \dfrac{3}{2} \right)^2 \) の違い
\( \dfrac{\;\;3^2}{2} \) は,分子の \( 3 \) だけが2個かけかけられた数
\( \dfrac{\;\;3^2}{2}=\dfrac{3 \times 3}{2}=\dfrac{9}{2} \)
\( \left( \dfrac{3}{2} \right)^2 \) は,\( \dfrac{3}{2} \) を2個かけた数
\( \left( \dfrac{3}{2} \right)^2=\dfrac{3}{2} \times \dfrac{3}{2}=\dfrac{9}{4} \)
と,どちらも「2分の3の2乗」と読めてしまいますが,異なる数を表しています。
指数を含む計算
指数を含む計算においては,最初に 指数を含む項を計算して指数を含まない形に書き直します。
例1 \( (-2)^2 \times 3 \) を計算する
\( (-2)^2 \) を指数を含まない形に書き直すと \( (-2)^2=(-2) \times (-2)=4 \) なので,
\( (-2)^2 \times 3= \{ (-2) \times (-2) \} \times 3 \)
\( =4 \times 3=12 \)
\( =12 \)
となります。
例2 \( -2^2 \times 3 \div (-4)^2 \) を計算する
\( -2^2 \) を指数を含まない形に書き直すと \( -2^2=-(2 \times 2)=-4 \)
\( (-4)^2 \) を指数を含まない形に書き直すと \( (-4)^2=(-4) \times (-4)=16 \)
なので,
\( -2^2 \times 3 \div (-4)^2= \{ -(2 \times 2) \} \times 3 \div \{ (-4) \times (-4) \} \)
\( =-4 \times 3 \div 16 \)
\( =-4 \times 3 \times \dfrac{1}{16} \)
\( =-\dfrac{4 \times 3}{16} \)
\( =-\dfrac{3}{4} \)
となります。
負の数を含む四則演算
たし算,ひき算,かけ算,わり算の4つをまとめて四則,また,四則を使った計算を四則演算と呼びます。
負の数を含む四則演算においても,算数のときと同じようにかっこの中やかけ算・わり算を先に計算するルールは適用されます。
四則演算における計算順序
四則演算における計算順序は次のとおりです。
2.指数を含む項を計算する
3.かけ算,わり算を計算する
4.たし算,ひき算を計算する
例1 \( (-4) \times 6-15 \div (-3) \) を計算する
\( (-4) \times 6-15 \div (-3)= \{ (-4) \times 6 \}-\{ 15 \div (-3) \} \)
\( =-24 – \left\{ 15 \times \left( -\dfrac{1}{3} \right) \right\} \)
\( =-24-(-5) \)
\( =-24+5 \)
\( =-19 \)
となります。
例2 \( -6-(3-5)^2 \div 4+(-2)^3 \times (-1) \) を計算する
\( -6-(3-5)^2 \div 4+(-2)^3 \times (-1)=-6-(-2)^2 \div 4+(-8) \times (-1) \)
\( =-6-\{ (-2) \times (-2) \} \div 4+(-8) \times (-1) \)
\( =-6-(4 \div 4)+8 \)
\( =-6- \left(4 \times \dfrac{1}{4} \right)+8 \)
\( =-6-1+8 \)
\( =1 \)
となります。
分配法則
かっこがあるかけ算の式では次の式が成り立ちます。
○ \( \times ( \) △ \( + \) □ \( )= \) ○ \( \times \) △ \( + \) ○ \( \times \) □
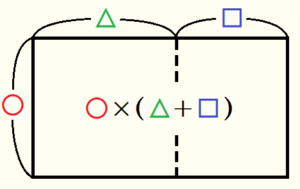
この式が成り立つ理由を 「縦の長さが ○ ,横の長さが △ の長方形」と「縦の長さが ○ ,横の長さが □ の長方形」をくっつけた長方形の面積として考えてみます。
大きい長方形を1個の長方形として面積を求める
「縦の長さが ○ ,横の長さが △ の長方形」と
「縦の長さが ○ ,横の長さが □ の長方形」を
くっつけた大きい長方形は
「縦の長さが ○ ,横の長さが △ \( + \) □ の長方形」
と考えられるので,その面積は
○ \( \times ( \) △ \( + \) □ \( ) \)
と表すことができます。
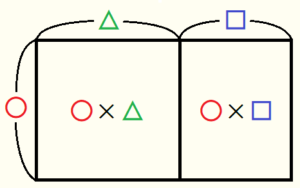
小さい長方形の面積の合計として面積を求める
「縦の長さが ○ ,横の長さが △ の長方形」の面積は
○ \( \times \) △
「縦の長さが ○ ,横の長さが □ の長方形」の面積は
○ \( \times \) □
と表すことができるので,大きい長方形の面積は
○ \( \times \) △ \( + \) ○ \( \times \) □
と表すことができます。
これらは,同じ長方形の面積を2通りの方法で表しているだけで,面積は等しいので,
○ \( \times ( \) △ \( + \) □ \( )= \) ○ \( \times \) △ \( + \) ○ \( \times \) □
となります。
ちなみに,乗法の結合法則より,
\( ( \) △ \( + \) □ \( ) \times \) ○ \( = \) △ \( \times \) ○ \( + \) □ \( \times \) ○
も成り立ちます。
負の数を含む場合も成り立つ
例として \( 2 \times \{ 3+(-4) \} \) と \( (-2+4) \times (-5) \) の場合を考えます。
例1 \( 2 \times \{ 3+(-4) \} \) を計算する
普通に計算すると・・・
\( 2 \times \{ 3+(-4) \}=2 \times (3-4) \)
\( =2 \times (-1) \)
\( =-2 \)
分配法則を使って計算すると・・・
\( 2 \times \{ 3+(-4) \}=2 \times 3 + 2 \times (-4) \)
\( =6+(-8) \)
\( =6-8 \)
\( =-2 \)
となり,どちらの計算方法でも \( -2 \) で結果は等しく,分配法則が成り立っていることがわかります。
例2 \( (-2+4) \times (-5) \) を計算する
普通に計算すると・・・
\( (-2+4) \times (-5)=2 \times (-5) \)
\( =-10 \)
分配法則を使って計算すると・・・
\( (-2+4) \times (-5)=(-2) \times (-5) + 4 \times (-5) \)
\( =10+(-20) \)
\( =10-20 \)
\( =-10 \)
となり,どちらの計算方法でも \( -10 \) で結果は等しく,分配法則が成り立っていることがわかります。


