大問1
問1 (1)~(3)の計算をしなさい。
(1) \( 9 \times (-6) \)
(2) \( -8+5 \div \dfrac{1}{3} \)
(3) \( (-\sqrt{6})^2+4 \)
問2 二次方程式 \( (x-2)(x-5)=0 \) を解きなさい。
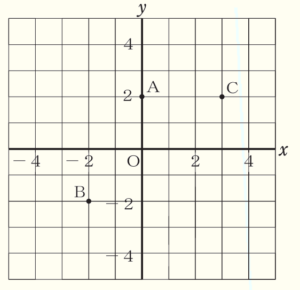
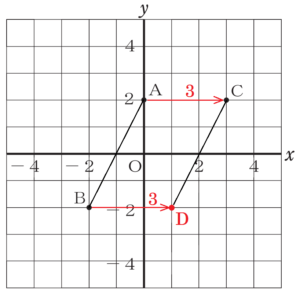
問3 右の図のような3点 \( A,B,C \) があります。点 \( D \) を,\( AB=CD,AC=BD \) である平行四辺形となるようにとるとき,点 \( D \) の座標を求めなさい。
ただし,点 \( O \) は原点とします。
問4 等式 \( 7x-y=4 \) を,\( y \) について解きなさい。
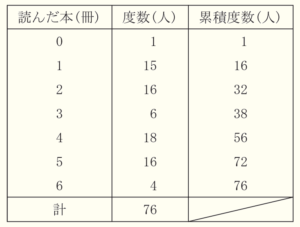
問5 下の表は,ある中学校の生徒 \( 76 \) 人に対し,夏休みに読んだ本の冊数を調べ,まとめたものです。表から,読んだ本の冊数の中央値を求めなさい。
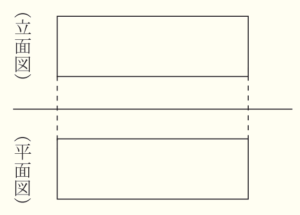
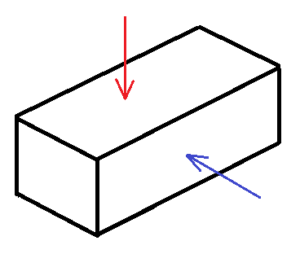
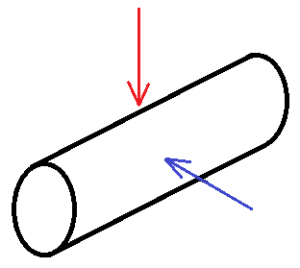
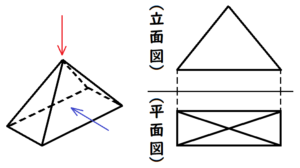
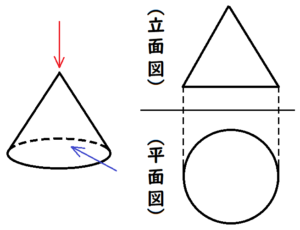
問6 右の図は,ある立体の投影図で,立面図と平面図は合同な長方形です。この投影図が表す立体として考えられるものを,ア~エからすべて選びなさい。
ア 四角柱
イ 四角錐
ウ 円柱
エ 円錐
大問2
箱の中に同じ大きさの赤玉と白玉がたくさん入っています。カイさんたちのクラスでは,この箱の中の玉を使って,確率や標本調査についての学習を行っています。
次の問いに答えなさい。
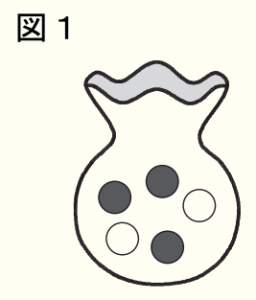
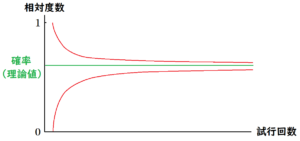
問1 カイさんとナオさんは,図1のように,箱の中の赤玉3個と白玉2個を袋に入れました。次に,「袋の中から玉を1個取り出し,色を確認してもとにもどす」という操作を多数回くり返し,赤玉が出る相対度数を調べました。
二人は,このときの相対度数の変化のようすについて,次のように説明しました。
操作を多数回くり返したとき,操作の回数が \( \boxed{ } \)。
\( \boxed{ } \) に当てはまる文として最も適当なものを,ア~オ から選びなさい。
ただし,この袋の中から玉を1個取り出すとき,どの玉が出ることも同様に確からしいとします。
ア 多くなっても,赤玉が出る相対度数のばらつきはなく,その値は \( 1 \) で一定である
イ 多くなっても,赤玉が出る相対度数のばらつきはなく,その値は \( 0.6 \) で一定である
ウ 多くなるにつれて,赤玉が出る相対度数のばらつきは小さくなり,その値は \( 1 \) に近づく
エ 多くなるにつれて,赤玉が出る相対度数のばらつきは小さくなり,その値は \( 0.6 \) に近づく
オ 多くなっても,赤玉が出る相対度数の値は大きくなったり小さくなったりして,一定の値には
近づかない
問2 トムさんたちのグループは,箱の中にある赤玉の個数を推定するため,先生から,箱の中に赤玉と白玉が合わせて \( 500 \) 個入っていることを聞き,次の手順で実験を行いました。
1 箱の中の玉全体をよくかき混ぜてから30個の玉を取り出し,取り出した玉にふくまれる赤玉の
個数を数える。
2 取り出した玉にふくまれる赤玉の個数の割合を計算する。
3 箱の中に取り出した玉をもどす。
次の(1),(2)に答えなさい。
(1) 手順の1で取り出した玉にふくまれる赤玉の個数が \( 12 \) 個であるとき,この箱の中には,赤玉がおよそ何個入っていたと推定されますか,求めなさい。また,その求め方を説明しなさい。
(2) トムさんたちは,実験を \( 10 \) 回行いました。さらに,トムさんたちは,手順の1で取り出す玉の個数を \( 60 \)個,\( 100 \) 個に変えた実験を、それぞれ \( 10 \) 回ずつ行いました。
最後に,箱の中にある赤玉の実際の個数を数え,箱の中にある赤玉の個数の割合を計算したところ,\( 0.3 \) であることがわかりました。
図2は,この計算結果と,取り出した玉にふくまれる赤玉の個数の割合を箱ひげ図にしたものを,まとめたものです。
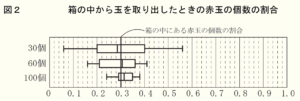
トムさんたちは,図2の特徴を読みとることで,箱の中にある赤玉の個数の割合と,取り出した玉にふくまれる赤玉の個数の割合の関係について,次のように説明しました。➀ の{ }に当てはまるものを,ア,イ から選び,また, ➁ に当てはまる言葉を書き入れ,説明を完成させなさい。
ただし,箱の中にある赤玉の個数の割合を「Aの割合」,取り出した玉にふくまれる赤玉の個数の割合を「Bの割合」とし, ➁ には,「Aの割合」,「Bの割合」という言葉を用いて書くこと。
図2では,手順の1で取り出す玉の個数を多くすれば多くするほど,四分位範囲は
➀ {ア 大きく イ 小さく}なり, ➁ という傾向がある。
大問3
泉さんたちは,電車がZ駅を出発してからの時間とZ駅からの道のりの関係を調べ,右の表にまとめました。
次に,泉さんたちは,電車がZ駅を出発してからの時間を \( x \) 秒,Z駅からの道のりを \( y \; m \) とし,表をもとに,コンピュータを使って,画面1のような5点 \( O,A,B,C,D \) としてグラフに表しました。
次の問いに答えなさい。

問1 泉さんたちは,表や画面1から \( y \) は \( x \) の2乗に比例すると考え,コンピュータを使って,\( x≧0 \) のときの関数 \( y=ax^2 \) (\( a \) は正の定数) のグラフが,5点 \( O,A,B,C,D \) の最も近くを通るときの \( a \) の値について調べました。その結果,画面2のように,\( a=0.5 \) のときが,5点 \( O,A,B,C,D \) の最も近くを通るグラフになると考えました。
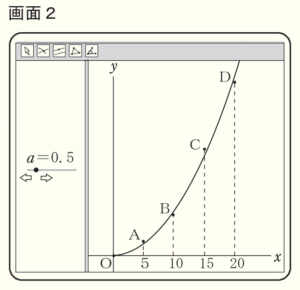
\( x \) と \( y \) の関係を,\( y=\dfrac{1}{2}x^2 \) として,次の(1),(2)に答えなさい。
ただし,\( 0≦x≦20 \) とします。
(1) 電車がZ駅を出発してからの道のりが \( 32 \; m \) になるのは,電車がZ駅を出発してから何秒後ですか, 求めなさい。
(2) 電車がZ駅を出発して,\( 4 \) 秒後から \( 8 \) 秒後までの間の平均の速さは秒速何 \( m \) ですか, 求めなさい。
問2 泉さんたちは,図1のように,Z駅の地点 \( P \) を出発する電車と,一直線にのびた線路に平行な道路を電車と同じ方向に走ってきて地点 \( Q \) を通過する自転車との位置関係について考えることにしました。
そこで,次のように条件を決めました。
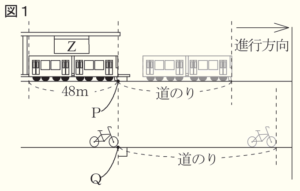
・ 電車が地点 \( P \) を出発すると同時に,走行中の自転車が地点 \( Q \) を通過する。
・ 電車が地点 \( P \) を出発してからの時間を \( x \) 秒,地点 \( P \) からの電車の道のりを \( y \; m \) とし,
電車の \( x \) と \( y \) の関係を \( y=\dfrac{1}{2}x^2 \) ・・・ ➀ とする。
・ 自転車が地点 \( Q \) を通過してからの時間を \( x \) 秒,地点 \( Q \) からの自転車の道のりを \( y \; m \) とし,
自転車の \( x \) と \( y \) の関係を \( y=10x \) ・・・ ② とする。
・ 電車の全長は, \( 48 \; m \) とする。
・ 地点 \( P,Q \) を通る直線は,線路と道路に垂直に交わるものとする。
泉さんたちは,コンピュータを使って,画面3のように,①と②のグラフを表しました。図2は,自転車が電車に追い越されたときの位置関係を示したものです。泉さんたちは,画面3と図2を見ながら,電車と自転車の位置関係について,話し合っています。

泉さん 「\( 20 \) 秒後に自転車は追いつかれちゃうんだね。」
岬さん 「図2のように,自転車が電車に追い越されるのは何秒後なんだろう。」
泉さん 「電車の全長がわかっているから,求めることができそうだね。」
図2のように,自転車が電車に追い越されるのは,自転車が地点 \( Q \) を通過してから何秒後ですか, 求めなさい。ただし,電車の最後尾 \( R \) と自転車の先端 \( S \) を通る直線は,線路と道路に垂直に交わるものとします。
大問4
図1のような長方形 \( ABCD \) があります。辺 \( AD \) 上に点 \( E \) を,\( BC=CE \) となるようにとります。ユウコさんたちは,この長方形を折ったときにできる図形について調べています。
次の問いに答えなさい。
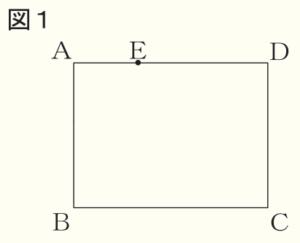
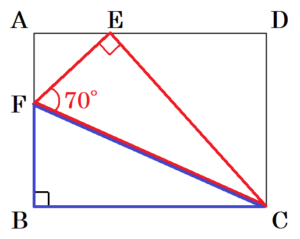
問1 図2のように,図1の長方形 \( ABCD \) を頂点 \( B \) が点 \( E \) と重なるように折ったときにできる折り目の線と辺 \( AB \) との交点を \( F \) とします。
(1) \( ∠CFE=70° \) のとき,\( ∠FCE \) の大きさを求めなさい。
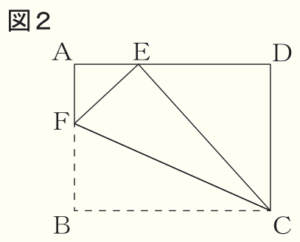
(2) ユウコさんたちは,それぞれのノートに長方形 \( ABCD \) をかき,点 \( E,F \) や折り目の線を作図しました。
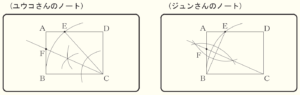
ユウコさんたちは,作図の方法について, 話し合っています。 ア , イ に当てはまる記号を,
ウ , エ に当てはまる言葉を,それぞれ書きなさい。ただし, ウ に当てはまる言葉は,下線部 のように,「〜の ・・・ をひく」という形で書くこと。
ユウコさん 「私はまず,頂点 ア を中心として,辺 イ の長さを半径とする
円をかいて点 \( E \) を作図したよ。次に,点 \( F \) と折り目の線を作図するために,
\( \underline{∠BCE} \) の二等分線をひくという方法で作図したよ。」
ジュンさん 「私も点 \( E \) の作図までは同じ方法だよ。そのあとに,点 \( F \) と折り目の線を作図する
ために, ウ という方法で作図したよ。」
ユウコさん 「実際に折ってみると,作図と同じ点 \( E,F \) や折り目の線になったね。作図の手順は
違うけど,私たちの折り目の線が同じになったのはなぜだろう。」
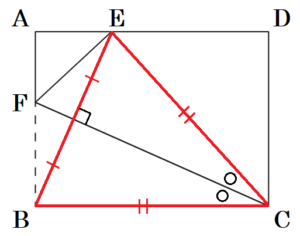
ジュンさん 「折り目の線が同じになるのは,\( △BCE \) が エ だからだよ。
ユウコさん 「なるほど! エ の性質が理由になるんだね。」
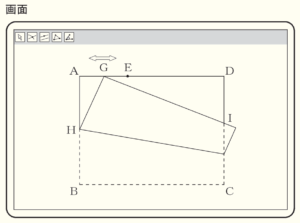
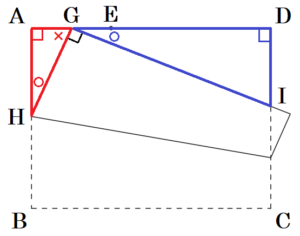
問2 ユウコさんたちは,コンピュータを使って,画面のように,線分 \( AE \) 上に点 \( G \) をとり,頂点 \( B \) と点 \( G \) が重なるように折ったときにできる折り目の線と辺 \( AB \) との交点を \( H \) とし,点 \( G \) を通り線分 \( GH \) に垂直な直線と辺 \( CD \) との交点を \( I \) としました。
次に,点 \( G \) を線分 \( AE \) 上で動かし,ユウコさんたちは,「\( △AGH \) と \( △DIG \) が相似である」と予想しました。
ユウコさんたちの予想が成り立つことを証明しなさい。
ただし,点 \( G \) は頂点 \( A \),点 \( E \) と重ならないものとします。
大問5
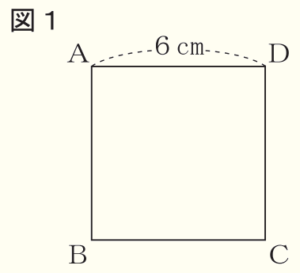
図1のような1辺の長さが \( 6 \; cm \) の正方形 \( ABCD \) があります。
次の問いに答えなさい。
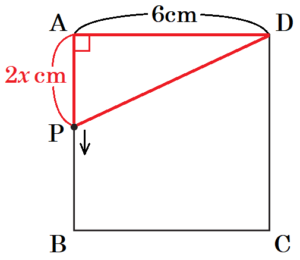
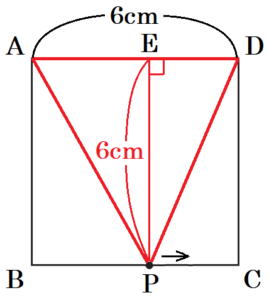
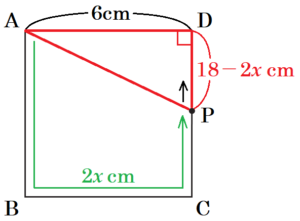
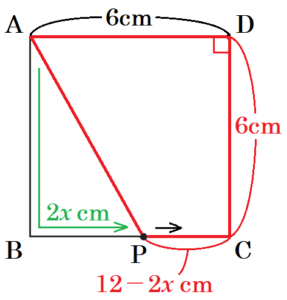
問1 図2のように、 図1の正方形 \( ABCD \) の辺上に点 \( P \) があり、点 \( P \) は, 頂点 \( A \) を出発して頂点 \( B,C \) を通って頂点 \( D \) まで毎秒 \( 2 \; cm \) の速さで動くものとします。
次の(1),(2)に答えなさい。
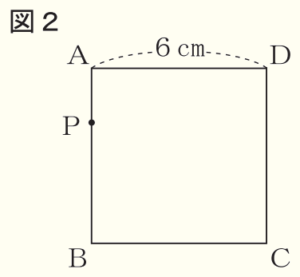
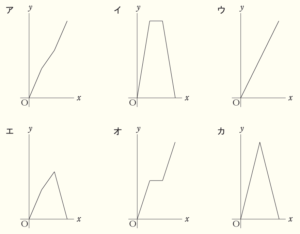
(1) 点 \( P \) が頂点 \( A \) を出発してから \( x \) 秒後の \( △ADP \) の面積を \( y \; cm^2 \) とするときの関係を表すグラフとして最も適当なものを, ア~カ から選びなさい。
ただし,点 \( O \) は原点とします。
(2) 点 \( P \) が辺 \( BC \) 上にあるとき,四角形 \( APCD \) が \( 20 \; cm^2 \) となるのは,点 \( P \) が頂点 \( A \) を出発してから何秒後ですか, 求めなさい。
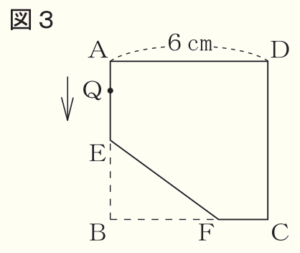
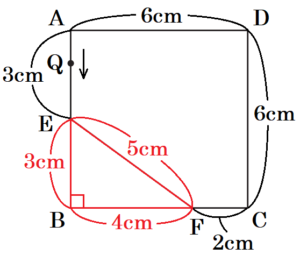
問2 図3のように,図1の正方形 \( ABCD \) の辺 \( AB,BC \) 上に, それぞれ点 \( E,F \) を,\( AE=3 \; cm,FC=2 \; cm \) となるようにとります。五角形 \( AEFCD \) の辺上に点 \( Q \) があります。点 \( Q \) は,頂点 \( A \) を矢印の方向に出発して,五角形 \( AEFCD \) の辺上を毎秒 \( 4 \; cm \) の速さで,ルールにしたがって動くものとします。
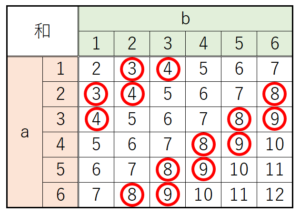
[ルール1] 点 \( Q \) は,大小2つのさいころを同時に投げたときの出た目の数の和をもとに,
五角形 \( AEFCD \) の辺上を動きます。
[ルール2] 出た目の数の和を点 \( Q \) が動く秒数とし,点 \( Q \) は,和の秒数の間だけ
五角形 \( AEFCD \) の辺上を動いて止まります。
点 \( Q \) は,\( 5 \) 秒間だけ五角形 \( AEFCD \) の辺上を動いて止まります。
大小2つのさいころを同時に投げるとき,点 \( Q \) が辺 \( CD \) 上に止まる確率を求めなさい。


-アイキャッチ-120x68.jpg)