大問1
(1) \( 8-17 \) を計算しなさい。
(2) \( 5(3a-2b)- (8a-4b) \) を計算しなさい。
【解説】
\( =15a-10b-8a+4b \)
\( =7a-6b \)
(3) \( 24ab \div (-4a) \times (-3b) \) を計算しなさい。
【解説】
\( =\dfrac{24ab \times (-3b)}{-4a} \)
\( =18b^2 \)
(4) \( (\sqrt{10}-\sqrt{5})^2 \) を計算しなさい。
【解説】
\( =(\sqrt{10})^2-2 \times \sqrt{10} \times \sqrt{5}+(\sqrt{5})^2 \)
\( =10-2\sqrt{50}+5 \)
\( =15-10\sqrt{2} \)
(5) 2次方程式 \( x^2+4x-1=0 \) を解きなさい。
【解説】
解の公式より,
\( x=\dfrac{-4±\sqrt{4^2-4 \times 1 \times (-1)}}{2} \)
\( =\dfrac{-4±\sqrt{20}}{2} \)
\( =\dfrac{-4±2\sqrt{5}}{2} \)
\( =-2±\sqrt{5} \)
(6) 赤玉2個,白玉4個が入っている袋がある。この袋から同時に2個の玉を取り出すとき,取り出した2個の玉の色が同じである確率を答えなさい。
【解説】
2個の赤玉に「赤1」,「赤2」,2個の白玉に「白1」,「白2」,「白3」,「白4」と名前をつけます。
取り出した2個の玉の組み合わせを樹形図に書き出し,同じ色になっている組み合わせに 〇 をつけると,
同じ色の組み合わせは \( 7 \) 通り,すべての組み合わせは \( 15 \) 通りなので,
求める確率は \( \dfrac{7}{15} \)
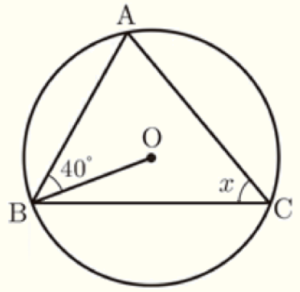
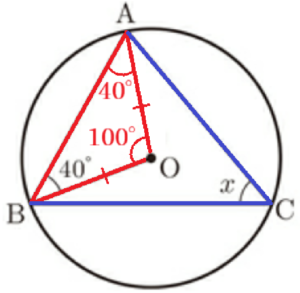
(7) 右の図のように,円 \( O \) の円周上に3つの点 \( A,B,C \) がある。\( ∠ABO=40° \) であるとき,\( ∠x \) の大きさを答えなさい。
【解説】
補助線 \( OA \) をひくと,\( △OAB \) は,
\( OA=OB \)(半径)の二等辺三角形なので,
\( ∠BAO=∠ABO=40° \)
であり,
\( ∠AOB=180°-(∠BAO+∠ABO) \)
\( =100° \)
\( ∠AOB \) は,\( \stackrel{\huge\frown}{ AB } \) に対する中心角,
\( ∠ACB \) は,\( \stackrel{\huge\frown}{ AB } \) に対する円周角なので,
\( ∠x=\dfrac{1}{2}∠AOB \)
\( =50° \)
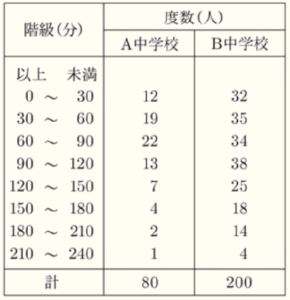
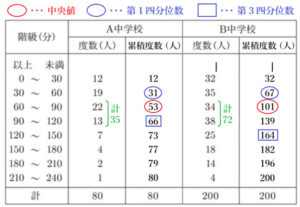
(8) 右の表は,A中学校の生徒 \( 80 \) 人と,B中学校の生徒 \( 200 \) 人の,ある日の家庭学習時間を調べ,度数分布表にまとめたものである。A中学校の生徒とB中学校の生徒の家庭学習時間を比べたとき,次の➀~➃の文について,正しいものには〇,誤っているものには×を,それぞれ書きなさい。
➀ 最頻値は,B中学校の方が大きい。
➁ 中央値は,同じ階級にある。
➂ 四分位範囲は,A中学校の方が大きい。
➃ 調べた生徒の人数に対する,家庭学習時間が \( 60 \) 分以上 \( 120 \) 分未満であった生徒の人数の割合は,
B中学校の方が大きい。
【解説】
➀ 最頻値とは,度数の値が最も大きい階級の階級値のことです。
A中学校で度数の値が最も大きい階級は,\( 60 \) 分以上 \( 90 \) 分未満の階級なので,
最頻値は \( \dfrac{60+90}{2}=75 \)(分)
B中学校で度数の値が最も大きい階級は,\( 90 \) 分以上 \( 120 \) 分未満の階級なので,
最頻値は \( \dfrac{90+120}{2}=105 \)(分)
なので,最頻値は,B中学校の方が大きい。
➁ A中学校は全部で \( 80 \) 人のデータを扱っているので,
中央値は,小さい方から \( 40 \) 番目と \( 41 \) 番目の値の平均値になります。
表に累積度数を書き足すと,\( 40 \) 番目と \( 41 \) 番目の値は,
\( 60 \) 分以上 \( 90 \) 分未満の階級に含まれています。
よって,A中学校の中央値は \( 60 \) 分以上 \( 90 \) 分未満の階級に含まれています。
B中学校は全部で \( 200 \) 人のデータを扱っているので,
中央値は,小さい方から \( 100 \) 番目と \( 101 \) 番目の値の平均値になります。
表に累積度数を書き足すと,\( 100 \) 番目と \( 101 \) 番目の値は,
\( 60 \) 分以上 \( 90 \) 分未満の階級に含まれています。
よって,B中学校の中央値は \( 60 \) 分以上 \( 90 \) 分未満の階級に含まれています。
以上より,A中学校とB中学校の中央値は,どちらも同じ階級に含まれています。
➂ 四分位範囲は,第3四分位数 \( – \) 第1四分位数で求めることができます。
A中学校の第1四分位数は,小さい方から \( 20 \) 番目と \( 21 \) 番目の値の平均値なので,
\( 30 \) 分以上 \( 60 \) 分未満の階級に含まれています。
第3四分位数は,小さい方から \( 60 \) 番目と \( 61 \) 番目の値の平均値なので,
\( 90 \) 分以上 \( 120 \) 分未満の階級に含まれています。
B中学校の第1四分位数は,小さい方から \( 50 \) 番目と \( 51 \) 番目の値の平均値なので,
\( 30 \) 分以上 \( 60 \) 分未満の階級に含まれています。
第3四分位数は,小さい方から \( 150 \) 番目と \( 151 \) 番目の値の平均値なので,
\( 120 \) 分以上 \( 150 \) 分未満の階級に含まれています。
以上より,A中学校とB中学校の第1四分位数は,同じ階級に含まれているのに対し,
A中学校の第3四分位数は,B中学校の第3四分位数よりも小さい階級に含まれているので,
四分位範囲は,A中学校の方が大きいとはいえません。
➃ A中学校で家庭学習時間が \( 60 \) 分以上 \( 120 \) 分未満の生徒の人数は,\( 22+13=35 \)(人)なので,
全体に占める割合は \( \dfrac{35}{80}=0,4375 \)
B中学校で家庭学習時間が \( 60 \) 分以上 \( 120 \) 分未満の生徒の人数は,\( 34+38=72 \)(人)なので,
全体に占める割合は \( \dfrac{72}{200}=0,36 \)
よって, 調べた生徒の人数に対する,家庭学習時間が \( 60 \) 分以上 \( 120 \) 分未満であった生徒の人数の
割合は,A中学校の方が大きくなっています。
大問2
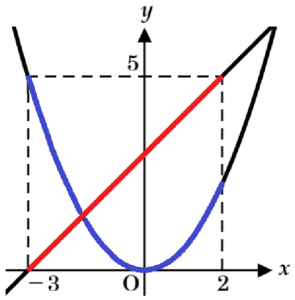
(1) 2つの関数 \( y=x+3 \) と \( y=ax^2 \) があり,\( x \) の変域が \( -3≦x≦2 \) のとき,この2つの関数の \( y \) の変域が一致する。このとき,\( a \) の値を求めなさい。
【解説】
関数 \( y=x+3 \) において,
\( x \) の変域が \( -3≦x≦2 \) のとき,
\( x=-3 \) のときの \( y \) の値は \( y=-3+3=0 \)
\( x=2 \) のときの \( y \) の値は \( y=2+3=5 \)
なので,\( y \) の変域は,\( 0≦y≦5 \) になります。
関数 \( y=ax^2 \) において,
\( y \) の値が \( 0 \) と正の値をとっていることから,
\( a>0 \) であることがわかります。
\( a>0 \) のとき,\( y \) の値が最大値をとるのは,
\( x \) の絶対値が最大になるときなので,
\( x=-3 \) のとき,\( y=5 \) になります。
\( y=ax^2 \) に \( x=-3,y=5 \) を代入すると,
\( 5=a \times (-3)^2 \)
\( a=\dfrac{5}{9} \)
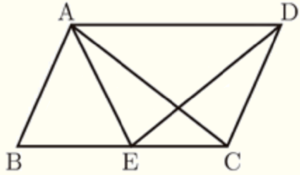
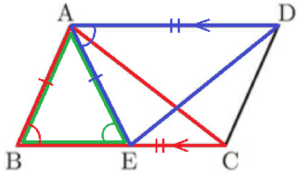
(2) 右の図のように,平行四辺形 \( ABCD \) があり,辺 \( BC \) 上に,\( AB=AE \) となる点 \( E \) をとる。このとき,\( △ABC≡△EAD \) であることを証明しなさい。
【解答】
\( △ABC \) と \( △EAD \) において,
仮定より,\( AB=EA \) ・・・ ➀
平行四辺形の向かい合う辺の長さは等しいので,
\( BC=AD \) ・・・ ➁
\( △ABE \) は二等辺三角形なので,
\( ∠ABC=∠AEB \) ・・・ ➂
平行四辺形の向かい合う辺は平行なので,
\( ∠EAD=∠AEB \) ・・・ ➃
➂➃より, \( ∠ABC=∠EAD \) ・・・ ➄
➀➁➄より,
2組の辺とその間の角がそれぞれ等しいので,
\( △ABC≡△EAD \)
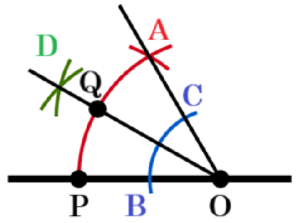
(3) 右の図のように,直線 \( l \) と,直線 \( l \) 上に2つの点 \( O,P \) がある。点 \( O \) を回転の中心として,点 \( P \) を時計回りの方向に \( 30° \) 回転移動させた点を \( Q \) とする。このとき,点 \( Q \) を,定規とコンパスを用いて作図しなさい。ただし,作図に使った線は消さないで残しておくこと。
\( \phantom{ } \)
\( \phantom{ } \)

【解答】
手順1 2点 \( O,P \) を中心に,線分 \( OP \) を半径と
する円弧を描く
(交点を \( A \) とします)
手順2 2点 \( O,A \) を通る直線を描く
手順3 点 \( O \) を中心に円弧を描く
(直線 \( l \),直線 \( OA \) との交点を \( B,C \) とします)
手順4 2点 \( B,C \) を中心に円弧を描く
(交点を \( D \) とします)
手順5 2点 \( O,D \) を通る直線を描く
手順5の直線と \( \stackrel{\huge\frown}{ AP } \) の交点が求める点 \( Q \) になります。
【解説】
点 \( Q \) は,点 \( P \) を時計回りの方向に \( 30° \) 回転移動させた点なので,
点 \( O \) を中心として,線分 \( OP \) を半径とする円周上の点で,
おうぎ形 \( POQ \) の中心角は \( 30° \) であることがわかります。
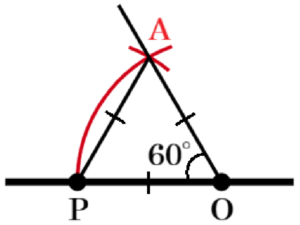
\( 30° \) は \( 60° \) の半分の大きさであることに注目すると,\( ∠AOP=60° \) となるような点 \( A \) を作図し,\( ∠AOP \) の二等分線を作図すればいいことになります。
正三角形の内角は \( 60° \) であることから,
2点 \( O,P \) からの距離が等しく,
\( OA=PA=OP \) となるような点 \( A \) を
作図することで,\( ∠AOP=60° \) となる
直線 \( OA \) を作図できます。
大問3
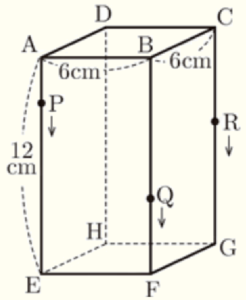
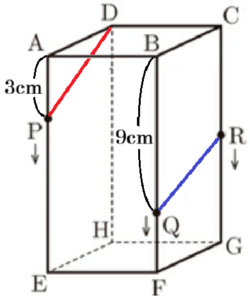
右の図のように,\( AB=BC=6 \; cm \),\( AE=12 \; cm \) の直方体 \( ABCD-EFGH \) がある。点 \( P \) は,頂点 \( A \) を出発し,毎秒 \( 1 \; cm \) の速さで,→\( \; \)の向きに辺 \( AE \) 上を \( 4 \) 秒間移動する。また,点 \( Q \) は,点 \( P \) と同時に頂点 \( B \) を出発し,毎秒 \( 3 \; cm \) の速さで,→\( \; \)の向きに辺 \( BF \) 上を頂点 \( F \) まで移動する。点 \( R \) は,点 \( P \) と同時に頂点 \( C \) を出発し,\( PD//QR \) となるように,→\( \; \)の向きに辺 \( CG \) 上を移動する。このとき,次の(1)~(4)の問いに答えなさい。
(1) 点 \( P \) が頂点 \( A \) を出発してから \( 1 \) 秒後の,立体 \( P-ABCD \) の体積を答えなさい。
【解説】
点 \( P \) が頂点 \( A \) を出発してから \( 1 \) 秒後の
\( AP \) の長さは \( 1 \; cm \) なので,
このときの立体 \( P-ABCD \) の体積は,
\( 6 \times 6 \times 1 \times \dfrac{1}{3}=12 \; (cm^3) \)
(2) 点 \( Q \) が頂点 \( B \) を出発してから \( 2 \) 秒後の,線分 \( DQ \) の長さを答えなさい。
【解答】
\( DQ=6\sqrt{3} \; cm \)
【解説】
点 \( Q \) が頂点 \( B \) を出発してから \( 2 \) 秒後の
\( BQ \) の長さは \( 6 \; cm \) なので,
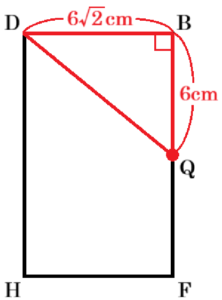
4点 \( D,H,F,B \) を通る面で切断したとき,
断面 \( DHFB \) は,右の図のようになります。
\( △DQB \) において,
\( BD \) は正方形 \( ABCD \) の対角線なので,
\( BD=6\sqrt{2} \; (cm) \)
であり,
三平方の定理より,
\( DQ^2=(6\sqrt{2})^2+6^2=108 \)
\( DQ=6\sqrt{3} \; (cm) \)(\( DQ>0 \) より)
(3) 点 \( R \) が頂点 \( C \) を出発してから \( 3 \) 秒後の,線分 \( CR \) の長さを答えなさい。
【解説】
点 \( P \) が頂点 \( A \) を出発してから \( 3 \) 秒後の
\( AP \) の長さは \( 3 \; cm \) ,
点 \( Q \) が頂点 \( B \) を出発してから \( 3 \) 秒後の
\( BQ \) の長さは \( 9 \; cm \) になります。
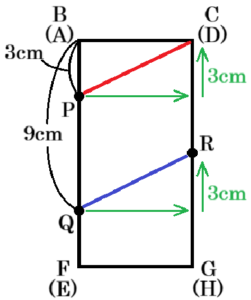
この直方体を面 \( BFGC \) が正面になるように
見た状態で,面 \( BFGC \) と面 \( AEHD \) を重ねると
右の図のようになります。
点 \( R \) は,\( PD//QR \) となるように動くので,
\( PD \) と \( QR \) の傾きは等しくなります。
点 \( D \) は,点 \( P \) より \( 3 \; cm \) 高い位置にあるので,
点 \( R \) は,点 \( Q \) より \( 3 \; cm \) 高い位置にあることになります。
よって,\( CR=6 \; cm \) になります。
(4) 3つの点 \( P,Q,R \) が同時に出発してからの \( 3 \) 秒間に,四角形 \( DPQR \) が動いてできる立体の体積を求めなさい。
【解説】
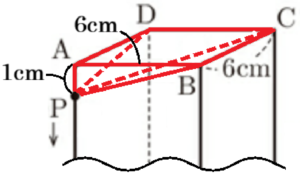
求める立体は下の図の赤の部分のような形になります。
この立体を3点 \( B,D,Q \) を通る面で切断すると,
四角すい \( D-APQB \) と四角すい \( D-BQRC \) の2つに分けることができます。
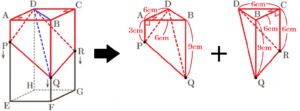
【四角すい \( D-APQB \) の体積】
台形 \( APQB \) を底面とすると,
\( \left\{ (3+9) \times 6 \times \dfrac{1}{2} \right\} \times 6 \times \dfrac{1}{3}=72 \; (cm^3) \)
【四角すい \( D-BQRC \) の体積】
台形 \( BQRC \) を底面とすると,
\( \left\{ (6+9) \times 6 \times \dfrac{1}{2} \right\} \times 6 \times \dfrac{1}{3}=90 \; (cm^3) \)
よって,求める立体の体積は
\( 72+90=162 \; (cm^3) \)
大問4
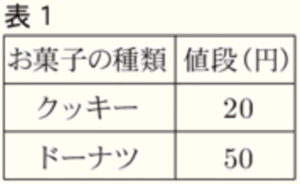
A高校の調理クラブは,お菓子を作って,B町のイベントで販売した。右の表1は,調理クラブが作ったお菓子の種類と,それぞれ \( 1 \) 個あたりの値段を示したものである。このとき,次の(1)~(3)の問いに答えなさい。
(1) B町のイベントを訪れたアオイさんは,クッキーを何個か買って家に持ち帰り,家族全員で同じ数ずつ分けることにした。\( 1 \) 人 \( 5 \) 個ずつ分けると \( 3 \) 個余り,\( 1 \) 人 \( 6 \) 個ずつ分けると \( 2 \) 個足りない。アオイさんの家族の人数と買ってきたクッキーの個数を,それぞれ求めなさい。
【解答】
家族の人数 ・・・ \( 5 \) 人
クッキーの個数 ・・・ \( 28 \) 個
【解説】
アオイさんの家族の人数を \( x \) 人として,買ってきたクッキーの個数を \( x \) を使った文字式で表すと,
\( 1 \) 人 \( 5 \) 個ずつ分けたときは \( 5x+3 \) 個,
\( 1 \) 人 \( 6 \) 個ずつ分けたときは \( 6x-2 \) 個,
と表すことができるので,
\( 5x+3=6x-2 \)
\( x=5 \)(人)
であり,\( 5x+3 \) に \( x=5 \) を代入すると,
\( 5 \times 5+3=28 \)(個)
(2) 次の文は,B町のイベントを訪れたヒナさんが,クッキーとドーナツを買おうとして,レオさんと相談している会話の一部である。この文を読んで,下の➀~➃の問いに答えなさい。
ヒナ:今日のイベントでは,A高校の調理クラブが作ったお菓子を買いたいんだ。
レオ:いくら分買おうと思っているの。
ヒナ:\( 1000 \) 円だよ。Ⅰ\( 1000 \) 円でおつりがなく,クッキーの個数とドーナツの個数に,できるだけ差が
ないように買うとすると,それぞれの個数は何個かな。
レオ:じゃあ,クッキーを \( x \) 個,ドーナツを \( y \) 個買うことにして方程式をつくると,
ア \( =1000 \)
となるね。
ヒナ:そうだね。レオさんがつくった方程式の,\( x \) も \( y \) も自然数になるような解を求めればいいね。
でも,1つの方程式に2つの文字が含まれているから,これだけで解を求められるのかな。
レオ:さっきつくった方程式 ア \( =1000 \) を
\( y= \) イ \( x+ \) ウ
に変形してみたよ。これで,何かわかるかな。
ヒナ:あ,そうか。\( x \) が エ の倍数であれば,\( y \) は整数になるね。
➀ ア に当てはまる式を,\( x \) と \( y \) を用いて表しなさい。
【解説】
\( 1 \) 個 \( 20 \) 円のクッキーを \( x \) 個買うのに必要な金額は \( 20x \) 円,
\( 1 \) 個 \( 50 \) 円のドーナツを \( y \) 個買うのに必要な金額は \( 50y \) 円
これらの合計が \( 1000 \) 円ちょうどなので,方程式は
\( 20x+50y=1000 \)
➁ イ , ウ に当てはまる値を,それぞれ答えなさい。
【解答】
イ ・・・ \( -\dfrac{2}{5} \)
ウ ・・・ \( 20 \)
【解説】
\( 20x+50y=1000 \) を \( y= \) の形に変形すると,
\( 20x+50y=1000 \)
\( 50y=-20x+1000 \)
\( y=-\dfrac{2}{5}x+20 \)
➂ エ に当てはまる最も小さい自然数を答えなさい。
【解説】
\( -\dfrac{2}{5}x+20 \) の値が整数になるのは,\( -\dfrac{2}{5}x \) の部分が整数になるときです。
つまり,約分して分母の \( 5 \) が消えればいいので,あてはまるのは,\( x \) の値が \( 5 \) の倍数のときです。
➃ 下線部分Ⅰのとき,クッキーとドーナツの個数はそれぞれ何個か,答えなさい。
【解答】
クッキーの個数 ・・・ \( 15 \) 個
ドーナツの個数 ・・・ \( 14 \) 個
【解説】
➂より,\( x \) の値が \( 5 \) の倍数になることがわかっているので,
\( x \) に \( 5,10,15,・・・ \) と順番に代入すると,
\( x=5 \) のとき ・・・ \( y=-\dfrac{2}{5} \times 5+20=18 \) → \( x \) と \( y \) の差は \( 13 \) 個
\( x=10 \) のとき ・・・ \( y=-\dfrac{2}{5} \times 10+20=16 \) → \( x \) と \( y \) の差は \( 6 \) 個
\( x=15 \) のとき ・・・ \( y=-\dfrac{2}{5} \times 15+20=14 \) → \( x \) と \( y \) の差は \( 1 \) 個
\( x=20 \) のとき ・・・ \( y=-\dfrac{2}{5} \times 20+20=12 \) → \( x \) と \( y \) の差は \( 8 \) 個
となり,以後,\( x \) の値はより大きく,\( y \) の値はより小さくなるので,
\( x \) と \( y \) の差は大きくなっていきます。
よって,求める答えは,クッキーが \( 15 \) 個,ドーナツが \( 14 \) 個になります。
(3) A高校の調理クラブでは,イベントで出た利益を使って,調理クラブの電子レンジを購入したいと考えている。次の文は,調理クラブのリオさん,サエさん,ユウさんが,次回のC市のイベントに向けて,打ち合わせを行っている会話の一部である。この文を読んで,あとの➀,➁の問いに答えなさい。ただし,原価とは,お菓子を作るのに必要な費用のことである。
リオ:B町のイベントでは,クッキーを \( 650 \) 個,ドーナツを \( 200 \) 個作って,すべて売り切れたよ。
どれくらい利益が出たのだろう。
サエ:クッキーとドーナツ,それぞれ \( 1 \) 個あたりの原価を下の表2にまとめたよ。
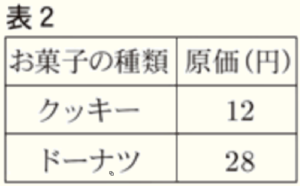
ユウ:B町のイベントでの,クッキーとドーナツの売上総額から原価の合計を引いて,利益を計算したら,
\( 9600 \) 円だったよ。
リオ:B町のイベントで出た利益だけでは,目標金額に \( 24000 \) 円足りないね。
サエ:それなら,C市のイベントでは,B町のイベントのときよりも作る個数を増やそうよ。
ユウ:それもいいけれど,\( 1 \) 個あたりの値段を上げることも考えられるね。
リオ:B町のイベントでの,クッキー \( 1 \) 個の値段に対する原価の割合を計算したら,\( 60 \; \% \) だったよ。
リオさんの計算
\( \dfrac{12}{20} \times 100=60 \; (\%) \)
ユウ:じゃあ,利益が目標金額に達するために,C市のイベントでは,Ⅱクッキーもドーナツも値段に対する
原価の割合を \( 40 \; \% \) にして,値段を決めてみたらどうかな。
➀ 下線部分Ⅱのとき,ドーナツ \( 1 \) 個の値段を答えなさい。
【解説】
リオさんの計算の式は
\( \dfrac{原価}{売価} \times 100=原価の割合 \; (\%) \)
になっているので,ドーナツ \( 1 \) 個の値段(売価)を \( x \) 円とすると,
\( \dfrac{28}{x} \times 100=40 \; (\%) \)
\( \dfrac{28}{x}=0.4 \)
\( 0.4x=28 \)
\( x=70 \)(円)
➁ C市のイベントでは,クッキーとドーナツを合わせて \( 1000 \) 個作り,値段に対する原価の割合を \( 40 \; \% \) にして販売することにした。作ったクッキーとドーナツをすべて売り切って,C市のイベントで \( 24000 \) 円の利益を出すとすると,クッキーとドーナツは,それぞれ何個作ればよいか,求めなさい。
【解答】
クッキーの個数 ・・・ \( 750 \) 個
ドーナツの個数 ・・・ \( 250 \) 個
【解説】
作るクッキーの個数を \( x \) 個,ドーナツの個数を \( y \) 個とし,
個数の関係を方程式で表すと,
\( x+y=1000 \) ・・・ ➀
利益の関係について,
クッキー \( 1 \) 個の原価の割合が \( 40 \; \% \) になるクッキーの値段を \( n \) 円とすると
\( \dfrac{12}{n} \times 100=40 \; (\%) \)
\( \dfrac{12}{n}=0.4 \)
\( n=30 \)(円)
であり,クッキー \( 1 \) 個を売って得られる利益は \( (30-12) \) 円なので,
\( x \) 個のクッキーを売って得られる利益を \( x \) を使った文字式で表すと,
\( (30-12)x \)(円)
ドーナツ \( 1 \) 個を売って得られる利益は \( (70-28) \) 円なので,
\( y \) 個のドーナツを売って得られる利益を \( y \) を使った文字式で表すと,
\( (70-28)y \)(円)
で,これらの合計が \( 24000 \) 円になるので,方程式で表すと,
\( (30-12)x+(70-28)y=24000 \) ・・・ ➁
➀➁を連立方程式にして解くと,
\( \left\{ \begin{array}{}
x+y=1000 \;\; ・・・ \;\; ➀ \\
(30-12)x+(70-28)y=24000 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁を整理すると,
\( 3x+7y=4000 \) ・・・ ➁’
➀ \( \times 3 \) すると,
\( 3x+3y=3000 \) ・・・ ➀’
➁’\( – \) ➀’すると,
\( 4y=1000 \)
\( y=250 \)(個)
➀に代入すると,
\( x+250=1000 \)
\( x=750 \)(個)
大問5
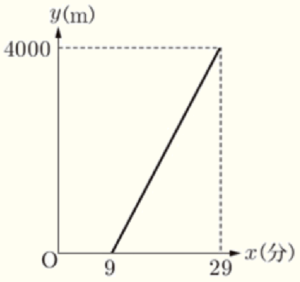
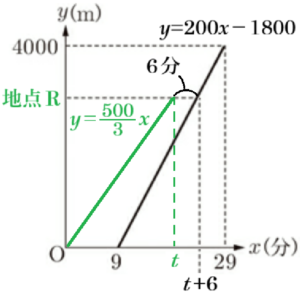
道路上に2つの地点 \( P,Q \) があり,\( P,Q \) 間の道のりは \( 4000 \; m \) である。ある日,ケンタさんが,午後2時に地点 \( P \) を出発して,地点 \( Q \) に向かって一定の速さで歩き続け,午後2時50分に地点 \( Q \) に到着した。また,同じ日に,サクラさんが,午後2時9分に地点 \( P \) を出発して,一定の速さで自転車で地点 \( Q \) に向かい,午後2時29分に地点 \( Q \) に到着した。
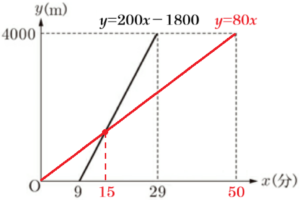
右の図は,地点 \( P \) から,午後2時 \( x \) 分に通過した地点までの道のりを \( y \; m \) として,サクラさんについて,\( x \) と\( y \) の関係をグラフに表したものである。このとき,次の(1)~(4)の問いに答えなさい。ただし,ケンタさんとサクラさんは,同じ道を通ったものとする。
(1) ケンタさんの歩いた速さは毎分何 \( m \) か,答えなさい。
【解説】
ケンタさんは,午後2時から午後2時50分までの50分間で \( 4000 \; m \) を歩いたので,
その速さは,
\( \dfrac{4000}{50}=80 \)
より,毎分 \( 80 \; m \)
(2) サクラさんについて,\( 9≦x≦29 \) のとき,\( y \) を \( x \) の式で表しなさい。
【解説】
求める直線の式を \( y=ax+b \) とすると,
\( a=\dfrac{4000-0}{29-9}=200 \)
\( y=200x+b \) に \( x=9,y=0 \) を代入すると,
\( 0=200 \times 9+b \)
\( b=-1800 \)
よって,求める直線の式は \( y=200x-1800 \)
(3) サクラさんがケンタさんに追いついたのは,午後2時何分か,求めなさい。
【解説】
ケンタさんが歩いた状態を関数で表すと \( y=80x \) になるので,
サクラさんがケンタさんに追いついた時間と場所は
2つの関数 \( y=200x-1800 \) と \( y=80x \) を連立方程式にして解いた解として求めることができます。
連立方程式を解くと,\( x=15 \) なので,
サクラさんがケンタさんに追いついたのは,午後2時15分になります。
\( \left\{ \begin{array}{}
y=200x-1800 \\
y=80x \\
\end{array} \right. \)
\( 200x-1800=80x \)
\( 120x=1800 \)
\( x=15 \)
(4) 同じ日に,ハルキさんが,午後2時に地点 \( P \) を出発し,地点 \( Q \) に向かって走った。ハルキさんが,休憩するために,地点 \( P \) と地点 \( Q \) の間にある地点 \( R \) で立ち止まったところ,その6分後に,サクラさんが自転車で地点 \( R \) を通過した。ハルキさんは,地点 \( R \) で10分間休憩した後,再び地点 \( Q \) に向かって走り,午後2時34分に地点 \( Q \) に到着した。ハルキさんが地点 \( R \) で休憩したのは,午後2時何分からか,求めなさい。ただし,ハルキさんは,サクラさんと同じ道を,休憩した時間以外は一定の速さで走ったものとする。
【解説】
ハルキさんは,地点 \( P \) から地点 \( Q \) までの \( 4000 \; m \) を
休憩時間10分を除く24分間で走ったので,ハルキさんが走った速さは,
毎分 \( \dfrac{4000}{24}=\dfrac{500}{3} \; (m) \) であったとわかります。
ここから,ハルキさんが地点 \( P \) から地点 \( R \) まで走った状態を
表す直線の式は \( y=\dfrac{500}{3}x \) になります。
ハルキさんが地点 \( R \) で休憩し始めた時間を
午後2時 \( t \) 分とすると,
サクラさんが地点 \( R \) を通過した時間は
午後2時 \( (t+6) \) 分と表すことができるので,
\( \dfrac{500}{3}t=200(t+6)-1800 \)
\( 500t=600(t+6)-5400 \)
\( 500t=600t+3600-5400 \)
\( 100t=1800 \)
\( t=18 \)(分)