大問1
(1) \( -4-5 \) を計算しなさい。
(2) \( a=3,b=2 \) のとき,\( 10a^2b \div 2a \) の値を求めなさい。
【解説】
\( 10a^2b \div 2a=\dfrac{10a^2b}{2a}=5ab \)
ここに \( a=3,b=2 \) を代入すると,
\( 5ab=5 \times 3 \times 2=30 \)
(3) 絶対値が \( 4 \) 以下の整数は何個あるか,求めなさい。
【解説】
絶対値とは,\( +,- \) の符号をはずした数のことなので,
絶対値が \( 4 \) になる整数は \( (+)4 \) と \( -4 \) です。
絶対値が \( 4 \) 以下の整数ということは,絶対値が \( 0,1,2,3,4 \) の整数なので,
あてはまるのは,\( -4,-3,-2,-1,0,1,2,3,4 \) の9個になります。
(4) \( y \) は \( x \) の2乗に比例し,\( x=-3 \) のとき \( y=36 \) である。\( x \) と \( y \) の関係を式に表しなさい。
【解説】
\( y \) が \( x \) の2乗に比例することを表す式は \( y=ax^2 \)(\( a \) は定数)になります。
この式に,\( x=-3,y=36 \) を代入すると,
\( 36=a \times (-3)^2 \)
\( 9a=36 \)
\( a=4 \)
よって,求める式は \( y=4x^2 \) になります。
(5) ある工場で大量に製造した品物から \( 400 \) 個を無作為に抽出して検査をすると,不良品が \( 3 \) 個あった。この工場で,\( 10000 \) 個の品物を製造したとき,そのうち不良品の個数は,およそ何個と推定されるか,求めなさい。
【解説】
標本調査では,
「母集団の中に含まれる不良品の割合」と「取り出したサンプルに含まれる不良品の割合」
は等しくなると考えられます。
\( 10000 \) 個の品物に含まれる不良品の個数を \( x \) 個とすると,
\( 10000:x=400:3 \)
\( 400x=30000 \)
\( x=75 \)(個)
(6) 内角の和が \( 1440° \) である多角形は何角形か,求めなさい。
【解説】
多角形の1つの頂点から対角線をひくと,いくつかの三角形をくっつけた形に分けることができます。
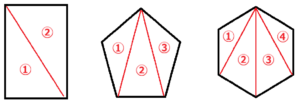
このことから,\( n \) 角形は対角線により \( n-2 \) 個の三角形に分けることができるので,
\( n \) 角形の内角の和は \( 180(n-2)° \) で表すことができます。
\( n \) 角形の内角の和が \( 1440° \) の場合は,
\( 180(n-2)=1440 \)
\( n-2=8 \)
\( n=10 \)
なので,十角形になります。
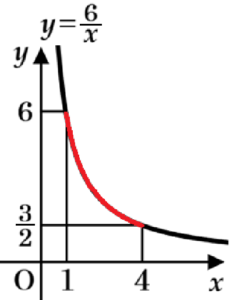
(7) 関数 \( y=\dfrac{6}{x} \) について,\( x \) の変域が \( 1≦x≦4 \) のときの \( y \) の変域を求めなさい。
【解答】
\( \dfrac{3}{2}≦y≦6 \)
【解説】
関数 \( y=\dfrac{6}{x} \) について,
\( x=1 \) のときの \( y \) の値は,
\( y=\dfrac{6}{1}=6 \)
\( x=4 \) のときの \( y \) の値は,
\( y=\dfrac{6}{4}=\dfrac{3}{2} \)
なので,\( y \) の変域は \( \dfrac{3}{2}≦y≦6 \) になります。
(8) 右の箱ひげ図は,あるクラスの生徒 \( 30 \) 人にそれぞれ \( 10 \) 点満点の国語と数学のテストを実施し,得点の分布を表したものである。この箱ひげ図から読みとれることとして,正しいといえるものはどれか,ア~エから2つ選びなさい。ただし,得点は整数とする。
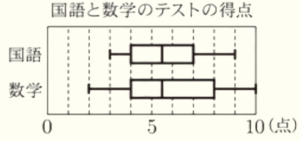
ア 国語と数学の平均点は同じである。
イ 数学が \( 5 \) 点以下の生徒は \( 15 \) 人である。
ウ 範囲も四分位範囲も,数学より国語の方が大きい。
エ \( 8 \) 点以上をとった生徒の人数は,国語より数学の方が多い。
【解説】
ア ・・・ 箱ひげ図の情報からだけでは平均点を判断することはできません。
イ ・・・ 全部で \( 30 \) 人のデータを集計しているので,
中央値は得点の低い方から15番目と16番目の平均値になります。
箱ひげ図から,中央値は \( 5.5 \) 点で,得点は整数であることから,
15番目の値は \( 5 \) 点以下,16番目の値は \( 6 \) 点以上です。
よって,数学が \( 5 \) 点以下の生徒は \( 15 \) 人になっています。
ウ ・・・ 範囲の大きさは箱ひげ図全体の長さ,四分位範囲の大きさは箱の長さで判断することができます。
箱ひげ図全体の長さ,箱の長さともに数学の方が長いので,
範囲,四分位範囲ともに数学の方が大きくなっています。
エ ・・・ 全部で \( 30 \) 人のデータを集計しているので,
第3四分位数は得点の高い方から8番目の値になります。
国語の第3四分位数は \( 7 \) 点なので,\( 8 \) 点以上をとった生徒の人数は,\( \color{blue}{7} \) 人以下です。
数学の第3四分位数は \( 8 \) 点なので,\( 8 \) 点以上をとった生徒の人数は,\( \color{red}{8} \) 人以上です。
よって,\( 8 \) 点以上をとった生徒の人数は,国語より数学の方が多いといえます。
(9) \( \sqrt{90n} \) の値が自然数となるような自然数 \( n \) のうち,2番目に小さいものを求めなさい。
【解説】
\( \sqrt{90n} \) の値が自然数となるのは,\( 90n=k^2 \)( \( k \) は整数)で表すことができるときです。
\( 90n \) を素因数分解すると \( 3^2 \times 2 \times 5 \times n \) なので,
\( 90n=k^2 \) で表すことができる最も小さい自然数 \( n \) は,\( n=10 \) です。
\( 90 \times 10=3^2 \times 2^2 \times 5^2=30^2 \)
次に \( 90n=k^2 \) で表すことができるのは,\( n=40=10 \times 2^2 \) のときです。
\( 90 \times 40=3^2 \times 2^4 \times 5^2=60^2 \)
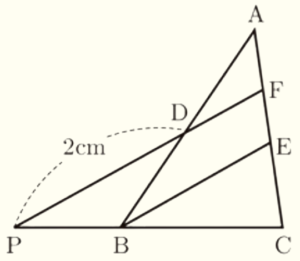
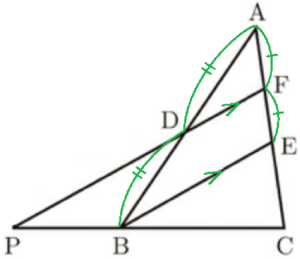
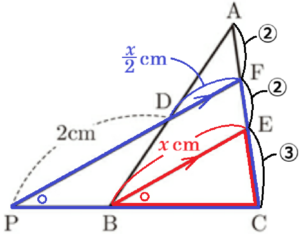
(10) 右の図のように,\( △ABC \) の辺 \( AB \) の中点を \( D \) とし,辺 \( AC \) 上に \( AE:EC=4:3 \) となるような点を \( E \) とする。線分 \( AE \) の中点を \( F \) とし,線分 \( CB \) と線分 \( FD \) をそれぞれ延長した直線の交点を \( P \) とする。
\( DP=2 \; cm \) であるとき,線分 \( BE \) の長さを求めなさい。
【解答】
\( BE=\dfrac{12}{7} \; cm \)
【解説】
\( △ADF \) と \( △ABE \) において,
点 \( D \) は辺 \( AB \) の中点,点 \( F \) は辺 \( AE \) の中点
なので,中点連結定理より,
\( DF//BE,DF=\dfrac{1}{2}BE \)
になっています。
\( △CBE \) と \( △CPF \) において,
\( DF//BE \) より,同位角は等しいので,
\( ∠CBE=∠CPF \)
共通な角なので,
\( ∠BCE=∠PCF \)
2組の角が等しいので,
\( △CBE \) ∽ \( △CPF \)
\( AE:EC=4:3,AF=FE \) より \( AF:FE:EC=2:2:3 \) なので,
\( CE:CF=3:5 \)
相似な三角形の対応する辺の比は等しいので,
\( BE:PF=CE:CF=3:5 \)
\( BE=x \; cm \) とすると,\( DF=\dfrac{x}{2} \; cm \) と表せるので,
\( BE:PF=3:5 \)
\( x:\left( 2+\dfrac{x}{2} \right)=3:5 \)
\( 5x=6+\dfrac{3}{2}x \)
\( 10x=12+3x \)
\( x=\dfrac{12}{7} \; (cm) \)
大問2
なつさんは,健康を維持するためには適度な運動が大切であると聞いて,どのくらいの運動をすればよいか調べたところ,身体活動量を数値で表す方法を厚生労働省のウェブサイトで見つけた。なつさんは調べたことをもとに,次の【メモ】と【身体活動の強度表】のようにまとめた。(1)~(3)に答えなさい。
【メモ】
〇 身体活動 ・・・ 安静にしている状態よりも多くのエネルギーを消費する活動のこと。
〇 メッツ ・・・ 身体活動の強度を表す単位。安静時を \( 1 \) メッツとして,身体活動が安静時の何倍の
エネルギーを消費するかで活動の強度を示している。
〇 エクササイズ ・・・ 身体活動量を表す単位。
○ 身体活動量の求め方

(例)テニス(\( 7 \) メッツ)を \( 1 \) 時間行ったときの身体活動量は \( 7 \times 1=7 \)(エクササイズ)
○ \( 3 \) メッツ以上の身体活動を,\( 1 \) 週間で合計 \( 23 \) エクササイズ行うことが推奨されている。
(1) バスケットボールを \( 20 \) 分間行ったときの身体活動量は何エクササイズになるか,求めなさい。

【解説】
\( 20 \) 分を時間に換算すると \( \dfrac{20}{60}=\dfrac{1}{3} \) 時間なので,
バスケットボール(\( 6 \) メッツ)を \( \dfrac{1}{3} \) 時間行ったときの身体活動量は
\( 6 \times \dfrac{1}{3}=2 \)(エクササイズ)
(2) なつさんは,月曜日から日曜日までの \( 7 \) 日間で合計 \( 23 \) エクササイズ行うことを目標にした。
今週の身体活動量を計算してみると,目標まであと \( 5 \) エクササイズ必要であることがわかった。日曜日に卓球となわとびを合計 \( 45 \) 分間して,目標を達成したい。ちょうど \( 5 \) エクササイズになるようにするには,卓球となわとびをそれぞれ何分間行えばよいか,求めなさい。
【解答】
卓球 ・・・ \( 30 \) 分間
なわとび ・・・ \( 15 \) 分間
【解説】
卓球を \( x \) 時間,なわとびを \( y \) 時間行うとすると,
\( 45 \) 分を時間に換算すると \( \dfrac{45}{60}=\dfrac{3}{4} \) 時間なので,
\( x+y=\dfrac{3}{4} \) ・・・ ➀
卓球の強度は \( 4 \) メッツ,なわとびの強度は \( 12 \) メッツなので,
合計の身体活動量は,
\( 4x+12y=5 \) ・・・ ➁
➀➁を連立方程式として解くと,
\( \left\{ \begin{array}{}
x+y=\dfrac{3}{4} \;\; ・・・ \;\; ➀ \\
4x+12y=5 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 4 \) すると,
\( 4x+4y=3 \) ・・・ ➀’
➁ \( – \) ➀’ すると,
\( 8y=2 \)
\( y=\dfrac{1}{4} \)
➀ に代入すると,
\( x+\dfrac{1}{4}=\dfrac{3}{4} \)
\( x=\dfrac{1}{2} \)
よって,卓球を \( \dfrac{1}{2} \) 時間,なわとびを \( \dfrac{1}{4} \) 時間行えばよいことになります。
これを分表記に換算すると,
卓球を行う時間は \( \dfrac{1}{2} \times 60=30 \) 分
なわとびを行う時間は \( \dfrac{1}{4} \times 60=15 \) 分
になります。
(3) なつさんの家の近くには,いろいろな運動ができる公園がある。公園の中に大きな池があり,池のまわりを走ることができる。ある日,なつさんは池のまわりを2周した。1周目は早歩きで歩き,2周目はランニングをして,合計 \( 30 \) 分間運動をした。ランニングの速さは,早歩きの速さの \( 1.5 \) 倍であったとすると,\( 30 \) 分間で行った身体活動量は何エクササイズになるか,求めなさい。
【解説】
【身体活動の強度表】から,早歩きの強度は \( 4 \) メッツ,ランニングの強度は \( 8.5 \) メッツなので,
早歩きを行った時間とランニングを行った時間がわかれば,身体活動量を求めることができます。
池のまわりの距離は変わらないので,ランニングの速さは,早歩きの速さの \( 1.5 \) 倍であったことから,
早歩きを行った時間はランニングを行った時間の \( 1.5 \) 倍であり,比で表すと,\( 3:2 \) になります。
早歩きを行った時間とランニングを行った時間の合計が \( 30 \) 分なので,
早歩きを行った時間は,\( 30 \times \dfrac{3}{5}=18 \) 分,つまり,\( \dfrac{18}{60}=\dfrac{3}{10} \) 時間
ランニングを行った時間は,\( 30 \times \dfrac{2}{5}=12 \) 分,つまり,\( \dfrac{12}{60}=\dfrac{1}{5} \) 時間
です。
ここから,合計の身体活動量は,
\( 4 \times \dfrac{3}{10}+8.5 \times \dfrac{1}{5}=1.2+1.7=2.9 \)(エクササイズ)
になります。
大問3
ひなたさんとみずきさんは,家にあるいろいろな時計の表示の仕方に興味をもち,調べることにした。(1)・(2)に答えなさい。
(1) 図1は,ひなたさんの家にあるデジタル時計であり,18時24分7秒を示している。このデジタル時計の表示について,2人が話し合っている。次の2人の【話し合いの一部】を読んで,( ア )・( イ )にあてはまる数をそれぞれ書きなさい。
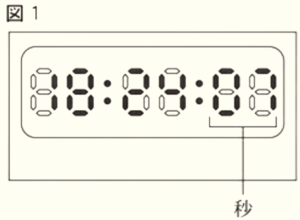
【話し合いの一部】
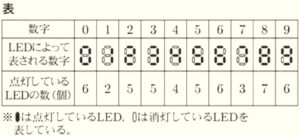
ひなたさん このデジタル時計は,図2のような7個のLEDが個別に
点灯したり消灯したりすることで,\( 0 \) から \( 9 \) までの数字
を表し,時刻を表示していますね。
みずきさん そうですね。\( 0 \) から \( 9 \) までのそれぞれの数字について,
LEDによって表される数字と,7個のLEDのうち
点灯しているLEDの個数をまとめると表のようになり
ますね。
\( \phantom{ } \)

ひなたさん デジタル時計の秒の2つの数字に注目して考えてみましょう。図1のように \( 7 \) 秒のときは
07のように2つの数字で表されて,14個のLEDのうち9個のLEDが同時に点灯
していますね。
みずきさん \( 0 \) 秒から \( 59 \) 秒のうち,最も多くのLEDが同時に点灯するのは( ア )秒のときで,
14個のLEDのうち13個のLEDが同時に点灯します。
ひなたさん 14個のLEDのうち10個のLEDが同時に点灯するのは \( 1 \) 分間に何回あるのでしょうか。
例えば10個のLEDが同時に点灯するような2つの数字の組み合わせには,「0と4」や
「5と5」がありますね。
みずきさん 2つの数字の組み合わせの中には,並び方によっては,デジタル時計の秒として表示されない
ものがありますね。それを除くと,14個のLEDのうち10個のLEDが同時に点灯
するのは \( 1 \) 分間に( イ )回ありますね。
【解答】
( ア )・・・ \( 8 \)
( イ )・・・ \( 13 \)
【解説】
( ア )
1つめの数字を表示するために点灯するLEDの個数を \( A \)
2つめの数字を表示するために点灯するLEDの個数を \( B \)
とすると,表より,最も多くのLEDが点灯するのは,\( (A,B)=(7,7) \) となるときで,
2つの数字の組み合わせは「88」になりますが,\( 88 \) 秒はないので,あてはまりません。
次に多くのLEDが点灯するのは,\( (A,B)=(6,7),(7,6) \) となるときで,
\( (A,B)=(6,7) \) となる2つの数字の組み合わせは,
「08,68,98」ですが,\( 68 \) 秒,\( 98 \) 秒はないので,あてはまるのは \( 8 \) 秒のときです。
\( (A,B)=(7,6) \) となる2つの数字の組み合わせは,
「80,86,89」ですが,\( 80 \) 秒,\( 86 \) 秒,\( 89 \) 秒はないので,どれもあてはまりません。
よって,最も多くのLEDが同時に点灯するのは \( 8 \) 秒のときになります。
( イ )
1つめの数字を表示するために点灯するLEDの個数を \( A \)
2つめの数字を表示するために点灯するLEDの個数を \( B \)
とすると,表より \( 2≤A≤7,2≤B≤7 \) であることから,
\( A+B=10 \) となる \( A,B \) の組み合わせは,
\( (A,B)=(3,7),(4,6),(5,5),(6,4),(7,3) \)
の5通りです。
\( (A,B)=(3,7) \) となる2つの数字の組み合わせは,
「78」ですが,\( 78 \) 秒はないのであてはまりません。
\( (A,B)=(4,6) \) となる2つの数字の組み合わせは,
「40,46,49」の3通り。
\( (A,B)=(5,5) \) となる2つの数字の組み合わせは,
「22,23,25,32,33,35,52,53,55」の9通り。
\( (A,B)=(6,4) \) となる2つの数字の組み合わせは,
「04,64,94」ですが,\( 64 \) 秒,\( 94 \) 秒はないので,あてはまるのは「04」の1通り。
\( (A,B)=(7,3) \) となる2つの数字の組み合わせは,
「87」ですが,\( 87 \) 秒はないのであてはまりません。
よって,10個のLEDが同時に点灯するのは,\( 1 \) 分間に \( 13 \) 回になります。
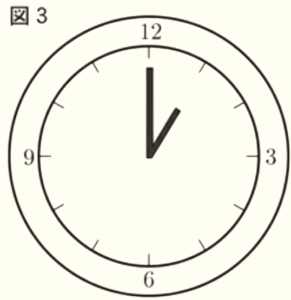
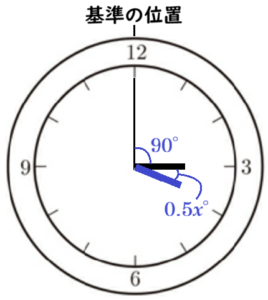
(2) 図3は,みずきさんの家にある長針と短針がそれぞれ一定の速さで動く円形のアナログ時計であり,午後1時を示している。(a)・(b)に答えなさい。
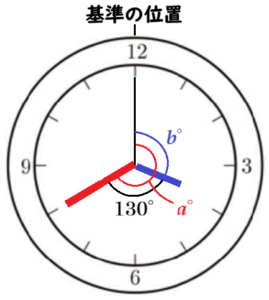
(a) みずきさんは,ある日の午後3時から午後4時の間で,長針と短針のつくる角度が \( 130° \) になる時刻について,【みずきさんの考え方】のように求めた。【みずきさんの考え方】の( ウ )にはあてはまる数を,
エ にはあてはまる \( x \) を用いた式を,それぞれ書きなさい。ただし,長針と短針のつくる角とは,長針と短針をそれぞれ線分と考えたときに,2つの線分がつくる角のうち角度が小さい方の角とする。
【みずきさんの考え方】
午後3時から午後4時の間で,長針と短針のつくる角度が \( 130° \) になる時刻を午後3時 \( x \) 分とする。午後3時の時点で,長針と短針のつくる角度は( ウ )°であり,そこから長針と短針が重なる
まで,長針と短針のつくる角度は小さくなっていく。長針と短針のつくる角度が \( 130° \) になるのは,
長針が短針を追い越した後である。
また,長針は \( 60 \) 分間で \( 360° \),短針は \( 60 \) 分間で \( 30° \) 動くので,\( 1 \) 分間で長針は \( 6° \),
短針は \( 0.5° \) 動く。これらのことから \( x \) についての方程式をつくると,
エ \( =130 \)
となり,これを解くと \( x=40 \) となり,\( 130° \) になる時刻は午後3時40分であることがわかる。
【解答】
( ウ ) ・・・ \( 90 \)
エ ・・・ \( 6x-(90+0.5x) \)
【解説】
午後3時の長針と短針の位置が異なるので,
0時(または0分)の位置を基準(仮に「基準の位置」と呼びます)にして,
午後3時 \( x \) 分に長針と短針が基準の位置からどれだけ回転した位置にあるかを考えます。
このとき,午後3時 \( x \) 分の長針の位置を
「基準の位置」から \( a° \) 回転した位置,
午後3時 \( x \) 分の短針の位置を
「基準の位置」から \( b° \) 回転した位置,
とすると,長針と短針のつくる角度は,
\( a-b \)
で表すことができます。
【午後3時 \( x \) 分の長針の位置】
長針は \( 1 \) 分間に \( 6° \) ずつ動くので,
午後3時 \( x \) 分には,「基準の位置」から \( 6x° \) 回転した位置にあります。
【午後3時 \( x \) 分の短針の位置】
午後3時には「基準の位置」から \( 90° \) 回転した
位置にあり,そこから \( 1 \) 分間に \( 0.5° \) ずつ動くので,
午後3時 \( x \) 分には,午後3時から \( 0.5x° \) 回転した位置、つまり,「基準の位置」から \( (90+0,5x)° \) 回転した位置にあります。
よって,長針と短針のつくる角度を \( x \) についての方程式で表すと,
\( 6x-(90+0.5x)=130 \)
となります。
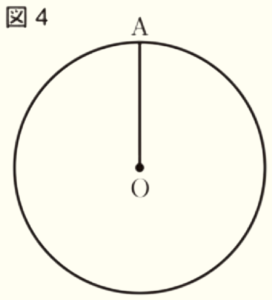
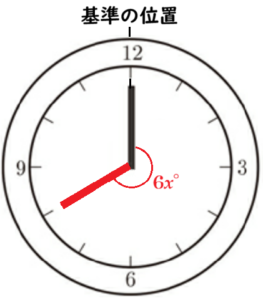
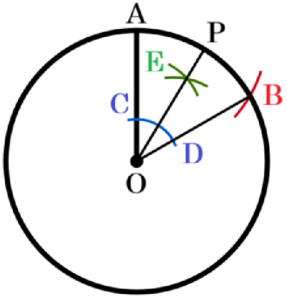
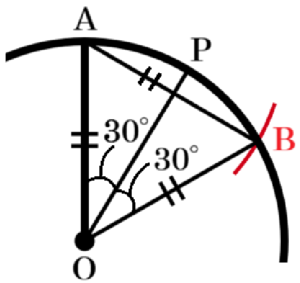
(b) 図4は,図3の時計の一部を模式的に表したものである。線分 \( OA \) がある時刻の長針を表しているとき,この時刻の \( 5 \) 分後の長針を表す線分 \( OP \) を,定規とコンパスの両方を使って作図しなさい。ただし,点 \( P \) は円 \( O \) の円周上にとることとし,作図に使った線は消さずに残しておくこと。また,定規やコンパスを持っていない場合は,作図の方法を文章で書きなさい。
【解答】
手順1 点 \( A \) を中心に線分 \( OA \) を半径とする円弧を描く
(円 \( O \) との交点を \( B \) とします)
手順2 線分 \( OB \) を描く
手順3 点 \( O \) を中心に円弧を描く
(線分 \( OA,OB \) との交点を \( C,D \) とします)
手順4 2点 \( C,D \) を中心に円弧を描く
(交点を \( E \) とします)
直線 \( OE \) と円 \( O \) の交点が求める点 \( P \) になります。
【解説】
長針は \( 1 \) 分間に \( 6° \) ずつ動くので,\( 5 \) 分で \( 30° \) 回転します。
つまり,線分 \( OP \) は線分 \( OA \) を時計回りに \( 30° \) 回転させたものになります。
\( 30° \) は \( 60° \) の半分の大きさなので,
線分 \( OA \) を時計回りに \( 60° \) 回転させた線分 \( OB \) を描き,\( ∠AOB \) の二等分線を描けばいいことになります。
また,\( ∠AOB=60° \) になるとき,\( △OAB \) は正三角形になるので,点 \( A \) を中心に線分 \( OA \) を半径とする円弧を描くことで \( AO=AB \) となる点 \( B \) の位置が求められます。
大問4
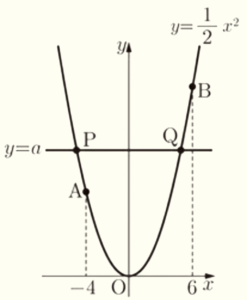
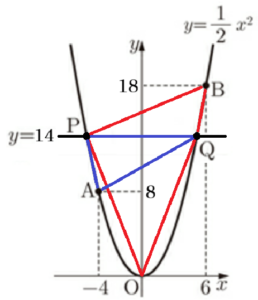
右の図のように,関数 \( y=\dfrac{1}{2}x^2 \) のグラフ上に2点 \( A,B \) があり,点 \( A \) の \( x \) 座標は \( -4 \),点 \( B \) の \( x \) 座標は \( 6 \) である。また,直線 \( y=a \; (a>0) \) と関数 \( y=\dfrac{1}{2}x^2 \) のグラフとの交点のうち,\( x \) 座標が小さい方を点 \( P \),\( x \) 座標が大きい方を点 \( Q \) とする。(1)~(4)に答えなさい。
(1) 直線 \( OB \) の式を求めなさい。
【解説】
点 \( B \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,\( x \) 座標は \( 6 \) なので,
\( y=\dfrac{1}{2} \times 6^2=18 \)
であり,点 \( B \) の座標は,\( B(6,18) \) です。
直線 \( OB \) の傾きを \( m \) とすると,
\( m=\dfrac{18-0}{6-0}=3 \)
よって,直線 \( OB \) の式は \( y=3x \) になります。
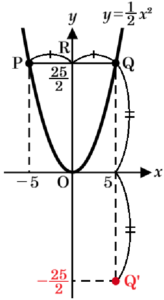
(2) \( PQ=10 \) のとき,\( x \) 軸を対称の軸として点 \( Q \) を対称移動した点の座標を求めなさい。
【解答】
\( \left( 5,-\dfrac{25}{2} \right) \)
【解説】
\( y=\dfrac{1}{2}x^2 \) のグラフは \( y \) 軸に対して左右対称なので,
\( PQ \) と \( y \) 軸の交点を \( R \) とすると,
\( PQ=10 \) のとき,\( PR=RQ=5 \) になります。
ここから,点 \( Q \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標は \( 5 \) なので,
\( y=\dfrac{1}{2} \times 5^2=\dfrac{25}{2} \)
より,点 \( Q \) の座標は,\( Q \left( 5,\dfrac{25}{2} \right) \) です。
求める点を \( Q’ \) とすると,
点 \( Q,Q’ \) の座標は,\( x \) 座標の値は等しく,
\( y \) 座標は符号を入れ替えた値になるので,
点 \( Q’ \) の座標は,\( Q’ \left( 5,-\dfrac{25}{2} \right) \) になります。
(3) \( a=14 \) のとき,四角形 \( OQBP \) の面積は \( △AQP \) の面積の何倍か,求めなさい。
【解説】
四角形 \( OQBP \) を \( △OQP \) と \( △BQP \) に分けると,
\( △AQP \) を含む3つの三角形はすべて線分 \( PQ \) を辺にもつので,
線分 \( PQ \) を底辺と考えると,高さの比が面積の比と等しくなります。
【\( △OQP \) の高さ】
原点 \( O \) の \( y \) 座標は \( 0 \),
点 \( P,Q \) の \( y \) 座標は \( 14 \) なので,
\( △OQP \) の高さは \( 14 \)
【\( △BQP \) の高さ】
原点 \( B \) の \( y \) 座標は \( 18 \),
点 \( P,Q \) の \( y \) 座標は \( 14 \) なので,
\( △BQP \) の高さは \( 4 \)
【\( △AQP \) の高さ】
点 \( A \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標は \( -4 \) なので,\( y \) 座標は,
\( y=\dfrac{1}{2} \times (-4)^2=8 \)
点 \( P,Q \) の \( y \) 座標は \( 14 \) なので,
\( △AQP \) の高さは \( 6 \)
ここから,四角形 \( OQBP \) と \( △AQP \) の面積比は,
四角形 \( OQBP: △AQP=(14+4):6=3:1 \)
よって,四角形 \( OQBP \) の面積は \( △AQP \) の面積の3倍になります。
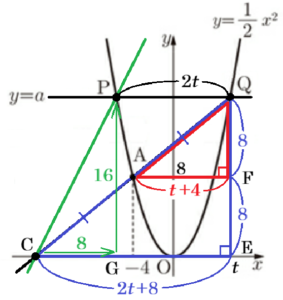
(4) 直線 \( AQ \) と \( x \) 軸との交点を \( C \) とする。点 \( A \) が線分 \( CQ \) の中点となるとき,直線 \( CP \) の傾きを求めなさい。
【解説】
点 \( Q \) から \( x \) 軸に垂線をひいた交点を \( E \),
点 \( A \) を通り,\( x \) 軸に平行な直線と線分 \( QE \) との交点を \( F \) とすると,
\( △QAF \) と \( △QCE \) は,点 \( A \) が線分 \( CQ \) の中点であることから,
\( △QAF \) ∽ \( △QCE \) ,相似比は \( 1:2 \) になっています。
点 \( Q \) の \( x \) 座標を \( t \) とすると,
線分 \( AF \) の長さは \( t+4 \) と表すことができるので,
線分 \( CE \) の長さは \( 2AF=2t+8 \) と表すことができます。
また,点 \( A \) の \( y \) 座標が \( 8 \) であることから,\( EF=8 \) であり,
相似比は \( 1:2 \) より,\( QF=8 \) になっています。
ここから,2点 \( P,Q \) の \( y \) 座標の値は \( 16 \) になります。
また,点 \( P \) から \( x \) 軸に垂線をひいた交点を \( G \) とすると,,
点 \( P \) の \( x \) 座標は \( -t \) と表せるので,\( PQ=2t \) と表すことができます。
このとき,\( CE=2t+8,GE=PQ=2t \) より,\( CG=8 \) になっています。
以上より,直線 \( CP \) の傾きは,
傾き \( =\dfrac{16}{8}=2 \)
大問5
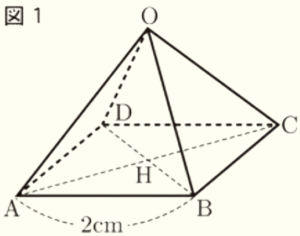
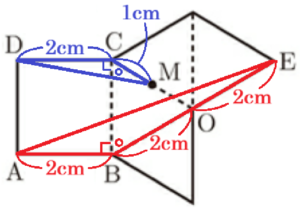
右の図1のように,すべての辺の長さが \( 2 \; cm \) の正四角錐 \( OABCD \) があり,底面の正方形 \( ABCD \) の対角線の交点を \( H \) とする。
(1)~(4)に答えなさい。
(1) \( △BCH \) の面積を求めなさい。
【解説】
\( △BCH,△ABH,△CDH,△ADH \) はすべて合同で,面積は等しいので,
正方形 \( ABCD \) の面積の \( \dfrac{1}{4} \) になります。
よって,
\( △BCH=\dfrac{1}{4} \times 2 \times 2=1 \; (cm^2) \)
(2) 3点 \( O,A,C \) を通る円の半径を求めなさい。
【解答】
\( \sqrt{2} \; cm \)
【解説】
\( △ABC \) は \( AB=BC=2 \; cm \) の直角二等辺三角形なので,
\( AC=2\sqrt{2} \; cm \)
\( △OAC \) は \( OA=OC=2 \; cm,AC=2\sqrt{2} \; cm \) なので,
\( ∠AOC=90° \) の直角二等辺三角形になっています。
\( ∠AOC \) は,3点 \( O,A,C \) を通る円の円周角なので,
\( ∠AOC=90° \) より,線分 \( AC \) は,この円の直径になります。
よって,この円の半径は,
\( \dfrac{1}{2}AC=\sqrt{2} \; (cm) \)
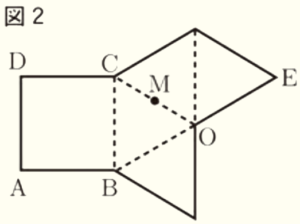
(3) 図2は,図1の正四角錐 \( OABCD \) の展開図である。図2のように,正四角錐 \( OABCD \) の \( △OAD \) の頂点 \( A \) が移る点を \( E \),線分 \( CO \) の中点をMとするとき,\( △ABE \) ∽ \( △MCD \) を証明しなさい。
【解答】
\( △ABE \) ∽ \( △MCD \) において,
すべての辺は \( 2 \; cm \) なので,
\( BE=BO+OE=4 \; cm \)
\( MC=\dfrac{1}{2}OC=1 \; cm \)
であり,
\( AB:MC=2:1 \) ・・・ ➀
\( BE:CD=4:2=2:1 \) ・・・ ➁
正方形の内角 \( ABCD \) の内角なので,
\( ∠ABC=∠DCB=90° \) ・・・ ➂
\( △OBC \) は正三角形なので,
\( ∠CBO=∠BCO=60° \) ・・・ ➃
➂➃より,
\( ∠ABE=∠ABC+∠CBO=150° \) ・・・ ➄
\( ∠MCD=∠DCB+∠BCO=150° \) ・・・ ⑥
➄⑥より,
\( ∠ABE=∠MCD \) ・・・ ➆
➀➁➆より,
2組の辺の比とその間の角がそれぞれ等しいので,
\( △ABE \) ∽ \( △MCD \)
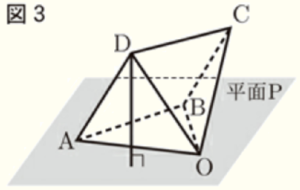
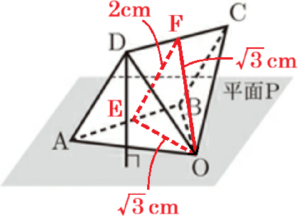
(4) 図3のように,\( △OAB \) が底面になるように,正四角錐 \( OABCD \) を平面 \( P \) 上に置いたとき,点 \( D \) と平面 \( P \) との距離を求めなさい。
【解答】
\( \dfrac{2\sqrt{6}}{3} \; cm \)
【解説】
線分 \( AB \) の中点を \( E \),線分 \( CD \) の中点を \( F \)
とし,点 \( F \) から線分 \( OE \) に垂線をひくと,
この垂線の長さは点 \( D \) と平面 \( P \) との距離と
等しくなります。
\( △OAE,△ODF \) は \( 30°,60°,90° \) の
直角三角形なので,
\( OE=OF=\dfrac{\sqrt{3}}{2} \times 2=\sqrt{3} \; (cm) \)
\( EF//AD \) なので,\( EF=AD=2 \; cm \)
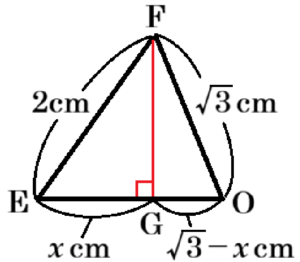
\( △OEF \) において,点 \( F \) から線分 \( OE \) に垂線を
ひいた交点を \( G \) とし,\( EG=x \; cm \) とすると,
三平方の定理より,
\( 2^2-x^2=(\sqrt{3})^2-(\sqrt{3}-x)^2 \)
\( 4-x^2=3-(3-2\sqrt{3}x+x^2) \)
\( 4-x^2=2\sqrt{3}x-x^2 \)
\( 2\sqrt{3}x=4 \)
\( x=\dfrac{2}{\sqrt{3}} \; (cm) \)
よって,
\( FG^2=2^2-\left( \dfrac{2}{\sqrt{3}} \right)^2=\dfrac{8}{3} \)
\( FG=\dfrac{2\sqrt{2}}{\sqrt{3}}=\dfrac{2\sqrt{6}}{3} \; (cm) \)( \( FG>0 \) より)