大問1
(1) \( 4-(-1)-8 \) を計算せよ。
【解説】
\( =4+1-8 \)
\( =5-8 \)
\( =-3 \)
(2) \( -6^2 \times \dfrac{1}{2}+(-4)^2 \) を計算せよ。
【解説】
\( =-36 \times \dfrac{1}{2}+16 \)
\( =-18+16 \)
\( =-2 \)
(3) \( \dfrac{x+2}{3}+\dfrac{3x-1}{4} \) を計算せよ。
【解答】
\( \dfrac{13x+5}{12} \)
【解説】
\( =\dfrac{4(x+2)}{12}+\dfrac{3(3x-1)}{12} \)
\( =\dfrac{4(x+2)+3(3x-1)}{12} \)
\( =\dfrac{4x+8+9x-3}{12} \)
\( =\dfrac{13x+5}{12} \)
(4) 等式 \( y=-5x+7 \) を \( x \) について解け。
【解答】
\( x=-\dfrac{1}{5}y+\dfrac{7}{5} \)
【解説】
等式 \( \boxed{ ? } \) を \( x \) について解くというのは,
\( x=\boxed{ ?? } \) の形に変形するということなので,
\( y=-5x+7 \)
\( 5x=-y+7 \)
\( x=-\dfrac{1}{5}y+\dfrac{7}{5} \)
(5) \( \sqrt{5}(\sqrt{2}+1)-\sqrt{45} \) を計算せよ。
【解答】
\( \sqrt{10}-2\sqrt{5} \)
【解説】
\( =\sqrt{5}(\sqrt{2}+1)-3\sqrt{5} \)
\( =\sqrt{10}+\sqrt{5}-3\sqrt{5} \)
\( =\sqrt{10}-2\sqrt{5} \)
(6) \( 4x^2-8x-12 \) を因数分解せよ。
【解説】
\( 4x^2-8x-12 \)
\( =4(x^2-2x-3) \)
\( =4(x+1)(x-3) \)
(7) 次の文中の \( \boxed{ } \) 内にあてはまる数を求めよ。
\( 5.3^2=28.09,5.4^2=29.16 \) であるから,\( \sqrt{29} \) を小数で表したときの小数第1位の数は \( \boxed{ } \) である。
【解説】
\( a^2>b^2 \; (a>0,b>0) \) が成り立つとき,\( a>b \) になります。
\( (\sqrt{29})^2=29 \) なので,\( 28.09<29<29.16 \) より,
\( 5.3^2<(\sqrt{29})^2<5.4^2 \) であり,\( 5.3<\sqrt{29}<5.4 \) になります。
ここから,\( \sqrt{29} \) は \( 5.3 \) より大きく \( 5.4 \) より小さい数なので,
\( \sqrt{29}=5.3〇〇 \) となり,小数第1位の数は \( 3 \) になります。
大問2
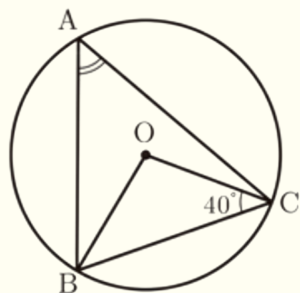
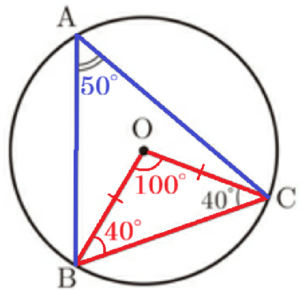
(1) 右の図のような円 \( O \) があり,異なる3点 \( A,B,C \) は円周上の点で,\( △ABC \) は鋭角三角形である。点 \( B \) と点 \( O \),点 \( C \) と点 \( O \) をそれぞれ結ぶ。
\( ∠OCB=40° \) であるとき,\( ∠BAC \) の大きさは何度か。
【解説】
\( △ABC \) は \( OB=OC \) の二等辺三角形なので,
\( ∠OBC=∠OCB=40° \) であり,
\( ∠BOC=180°-(∠OBC+∠OCB) \)
\( =180°-(40°+40°) \)
\( =100° \)
\( ∠BAC \) は \( \stackrel{\huge\frown}{ BC } \) に対する円周角,\( ∠BOC \) は \( \stackrel{\huge\frown}{ BC } \) に対する中心角なので,
\( ∠BAC=\dfrac{1}{2}∠BOC \)
\( =\dfrac{1}{2} \times 100° \)
\( =50° \)
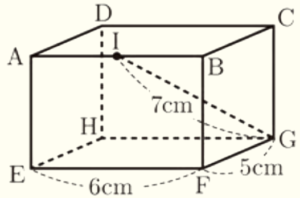
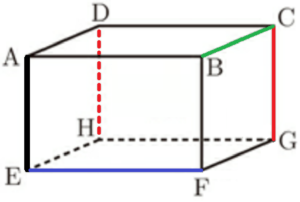
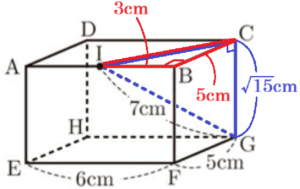
(2) 右の図のような直方体がある。辺 \( AB \) の中点を \( I \) とし,点 \( G \) と点 \( I \) を結ぶ。
\( EF=6 \; cm,FG=5 \; cm,GI=7 \; cm \) であるとき,次のア,イの問いに答えよ。
ア 次の \( \boxed{ア} \; \)~\( \; \boxed{エ} \)の直線のうち,直線 \( AE \) とねじれの位置にある直線はどれか。正しいものを1つ選んで,その記号を書け。
\( \boxed{ア} \) 直線 \( BC \) \( \boxed{イ} \) 直線 \( CG \)
\( \boxed{ウ} \) 直線 \( DH \) \( \boxed{エ} \) 直線 \( EF \)
【解答】
\( \boxed{ア} \) 直線 \( BC \)
【解説】
ねじれの位置にある直線とは,
どこまで伸ばしても交わらない直線のうち,平行ではないもののことです。
直線 \( EF \) は,直線 \( AE \) と点 \( E \) で交わっている,
直線 \( CG \),直線 \( DH \) は,直線 \( AE \) と平行
ので,ねじれの位置にはありません。
イ この直方体の体積は何 \( \; cm^3 \) か。
【解答】
\( 30\sqrt{15} \; cm^3 \)
【解説】
\( △CBI \) において,三平方の定理より,
\( CI^2=BC^2+BI^2 \)
\( =5^2+3^2 \)
\( =34 \)
\( △GCI \) において,三平方の定理より,
\( CG^2=GI^2-CI^2 \)
\( =7^2-34 \)
\( =15 \)
\( CG=\sqrt{15} \; (cm) \)(\( CG>0 \) より)
よって,この直方体の体積は
\( 5 \times 6 \times \sqrt{15}=30\sqrt{15} \; (cm^3) \)
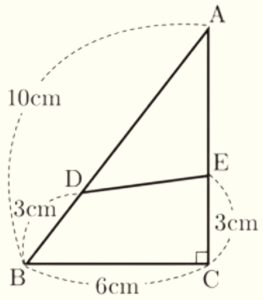
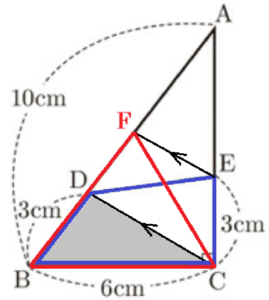
(3) 右の図のような,\( ∠ACB=90° \) の直角三角形 \( ABC \) があり,\( AB=10 \; cm,BC=6 \; cm \) である。点 \( D \) は辺 \( AB \) 上の点で,\( BD=3 \; cm \) である。点 \( E \) は辺 \( AC \) 上の点で,\( CE=3 \; cm \) である。点 \( D \) と点 \( E \) を結ぶ。
線分 \( AD \) 上に点 \( F \) を,四角形 \( BCED \) の面積と \( △BCF \) の面積が等しくなるようにとるとき,線分 \( DF \) の長さは何 \( cm \) か。
【解答】
\( DF=\dfrac{21}{8} \; cm \)
【解説】
四角形 \( BCED \) と \( △BCF \) は,
\( △BCD \) の部分が共通なので,
四角形 \( BCED=△BCD+△CDE \)
\( △BCF=△BCD+△CDF \)
と考えると,
四角形 \( BCED \) の面積と \( △BCF \) の面積が等しくなるとき,\( △CDE \) の面積と \( △CDF \) の面積は等しくなります。
\( △CDE \) と \( △CDF \) は辺 \( CD \) が共通なので,等積変形の考え方から,\( EF//CD \) になるとき,\( △CDE \) の面積と \( △CDF \) の面積は等しくなります。
\( EF//CD \) のとき,
\( ∠AFE=∠ADC,∠A \) は共通,
より,
\( △AFE \) ∽ \( △ADC \) になります。
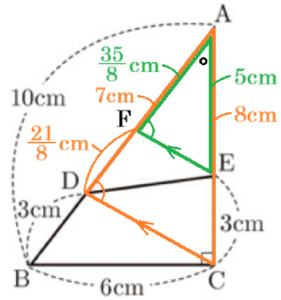
\( △ABC \) において,三平方の定理より,
\( AC^2=10^2-6^2=64 \)
\( AC=8 \; (cm) \)
\( CE=3 \; cm \) より,
\( AE=8-3=5 \; (cm) \)
\( AB=10 \; cm,BD=3 \; cm \) より,
\( AD=10-3=7 \; (cm) \)
相似な三角形の対応する辺の比は等しいので,
\( AF:AD=AE:AC \)
\( AF:7=5:8 \)
\( AF=\dfrac{35}{8} \; (cm) \)
であり,
\( DF=7-\dfrac{35}{8}=\dfrac{21}{8} \; (cm) \)
大問3
(1) \( y \) は \( x \) に比例し,\( x=4 \) のとき \( y=-2 \) である。\( x=8 \) のときの \( y \) の値を求めよ。
【解説】
\( y \) は \( x \) に比例することを表す式は,\( y=ax \)(\( a \) は定数) です。
\( y=ax \) に \( x=4,y=-2 \) を代入すると,
\( -2=a \times 4 \)
\( a=-\dfrac{1}{2} \)
\( y=-\dfrac{1}{2}x \) に \( x=8 \) を代入すると,
\( y=-\dfrac{1}{2} \times 8=-4 \)
(2) 数字を書いた5枚のカード \( \boxed{1},\boxed{2},\boxed{2},\boxed{3},\boxed{5} \) がある。この5枚のカードをよくきって,その中から1枚ずつ続けて2回引き,はじめに引いたカードに書いてある数を \( a \),次に引いたカードに書いてある数を \( b \) とする。このとき,\( 2a+b=5 \) が成り立つ確率を求めよ。
【解説】
\( a,b \) の組み合わせとそれぞれにおける \( 2a+b \) の値を樹形図にして書き出すと,
下の図のようになります。
\( 2a+b=5 \) になる組み合わせは \( 3 \) 通り,すべての組み合わせは \( 20 \) 通りなので,
求める確率は \( \dfrac{3}{20} \)

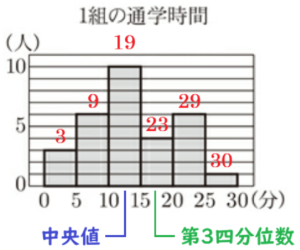
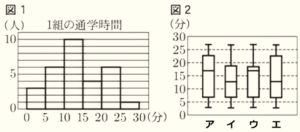
(3) 花子さんは,1組から4組の各クラスの生徒 \( 30 \) 人の通学時間を調べ,そのデータを,組ごとに,ヒストグラムと箱ひげ図にそれぞれ表した。下の図1のヒストグラムは,1組のヒストグラムである。下の図2のア~エの箱ひげ図は,1組から4組の箱ひげ図のいずれかに対応している。図2のア~エの箱ひげ図のうち,1組の箱ひげ図はどれか。正しいものを1つ選んで,その記号を書け。
【解説】
図2の
ア~
エの箱ひげ図は,最小値,第1四分位数,最大値は4つすべてで同じ階級にあるので,
違いがみられる中央値と第3四分位数がヒストグラムでどの階級に属しているかを見ていきます。
各クラスの生徒数は \( 30 \) 人なので,
中央値は,小さい方から15番目と16番目の値の平均値,
第3四分位数は,小さい方から23番目の値,
になります。
図1のヒストグラムに累積度数を書き込むと
右の図のようになり,
15番目と16番目の値が含まれている階級は
\( 10 \) 分以上 \( 15 \) 分未満の階級,
23番目の値が含まれている階級は
\( 15 \) 分以上 \( 20 \) 分未満の階級,
なので,これらを満たしている箱ひげ図は
イの箱ひげ図になります。
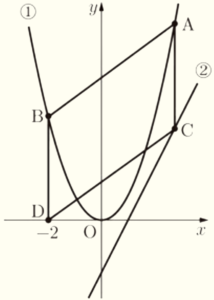
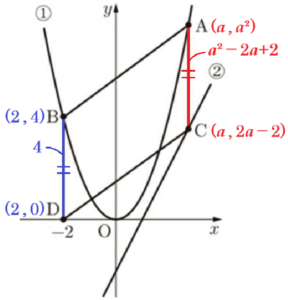
(4) 右の図で,点 \( O \) は原点であり,放物線➀は関数 \( y=x^2 \) のグラフで,直線➁は関数 \( y=2x-2 \) のグラフである。
2点 \( A,B \) は放物線➀上の点で,点 \( A \) の \( x \) 座標は正の数であり,点 \( B \) の \( x \) 座標は \( -2 \) である。点 \( A \) を通り,\( y \) 軸に平行な直線をひき,直線➁との交点を \( C \) とする。また,点 \( B \) を通り,\( y \) 軸に平行な直線をひき,\( x \) 軸との交点を \( D \) とする。点 \( A \) と点 \( B \),点 \( C \) と点 \( D \) をそれぞれ結ぶ。
これについて,次のア,イの問いに答えよ。
ア 関数 \( y=x^2 \) で,\( x \) の変域が \( -1≦x≦2 \) のとき,\( y \) の変域を求めよ。
【解説】
二次関数 \( y=ax^2 \)(\( a>0,a \) は定数)のグラフにおいて,
\( x \) の変域が \( 0 \) を含むとき,\( y \) の最小値は \( 0 \) になります。
また,\( x \) の絶対値が最も大きくなるとき,\( y \) の値は最大値をとります。
\( y=x^2 \) で,\( x \) の変域が \( -1≦x≦2 \) のとき,
\( 0 \) を含んでいるので,\( y \) の最小値は \( 0 \) になります。
また,\( x \) の絶対値が最も大きくなるのは \( x=2 \) のときなので,
\( y \) の最大値は,
\( y=2^2=4 \)
よって,求める \( y \) の変域は \( 0≦y≦4 \) になります。
イ 四角形 \( ABDC \) が平行四辺形であるとき,点 \( A \) の \( x \) 座標はいくらか。点 \( A \) の \( x \) 座標を \( a \) として,\( a \) の値を求めよ。\( a \) の値を求める過程も,式と計算を含めて書け。
【解答】
平行四辺形の向かい合う辺の長さは等しいので,\( AC=BD \) である。
点 \( A \) は \( y=x^2 \) 上の点で,
\( x \) 座標は \( a \) なので,\( y \) 座標は,
\( y=a^2 \)
点 \( C \) は \( y=2x-2 \) 上の点で,
\( x \) 座標は \( a \) なので,\( y \) 座標は,
\( y=2a-2 \)
と表すことができる。
ここから,
\( AC=a^2-2a-2 \)
と表すことができる。
点 \( B \) の \( y \) 座標は,
\( y=(-2)^2=4 \)
なので,\( BD=4 \) である。
よって,\( BD=AC \) だから,
\( a^2-2a+2=4 \)
\( a^2-2a-2=0 \)
\( a=1+\sqrt{3} \)(\( a>0 \) より)
大問4
(1) 次の会話文を読んで,あとのア,イの問いに答えよ。
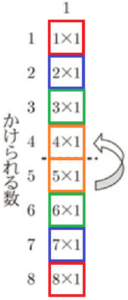
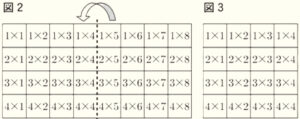
先生:図1のような,かけられる数とかける数がそれぞれ \( 1 \) から \( 8 \) まで書かれたかけ算の表があります。
このかけ算の表の「\( 1 \times 1 \)」と「\( 8 \times 1 \)」,「\( 1 \times 8 \)」と「\( 8 \times 8 \)」の位置が重なるように点線で
半分に折り,図2のような二つ折りにします。次に,「\( 1 \times 1 \)」と「\( 1 \times 8 \)」の位置が重なるように
点線で半分に折り,図3のような四つ折りにします。このように四つ折りにしたとき,「\( 1 \times 1 \)」と
位置が重なるかけ算は,「\( 8 \times 1 \)」,「\( 1 \times 8 \)」,「\( 8 \times 8 \)」で,この4つのかけ算の値の和は \( 81 \)
です。では,「\( 2 \times 3 \)」と位置が重なるかけ算の式は,どうなりますか。

花子:「\( 2 \times 3 \)」と位置が重なるかけ算は,「\( 7 \times 3 \)」と他に2つあります。この4つのかけ算の値の和は,
\( 6+21+12+42 \) で \( 81 \) です。位置が重なる4つのかけ算の値の和はどこでも \( 81 \) なのでしょうか。
先生:では,それを調べるために文字式を使って考えましょう。四つ折りにしたとき,「\( a \times b \)」と位置が
重なるかけ算の式を \( a,b \) を使って表すと,「\( a \times b \)」以外の式はどう表されますか。
花子:「( P ) \( \times b \)」と「 \( a \times \) ( Q )」と「( P ) \( \times \) ( Q )」です。
先生:その通りです。この4つのかけ算の値の和を求めると \( 81 \) ですから,位置が重なる4つのかけ算の
値の和はどこでも \( 81 \) であることがわかりましたね。
では、かけられる数とかける数がそれぞれ \( 1 \) から R まで書かれたかけ算の表を,同じように
四つ折りにすると,位置が重なる4つのかけ算の値の和は,どうなりますか。
花子:計算してみます・・・・・ ,先生,\( 2025 \) になりました。
先生:正しく求められましたね。
ア 会話文中の P にあてはまる式は何か。\( a \) を使った式で表せ。また,会話文中の Q にあてはまる式は何か。\( b \) を使った式で表せ。
【解答】
P ・・・ \( 9-a \)
Q ・・・ \( 9-b \)
【解説】
P
かける数を \( 1 \) に固定して,図1のように折り返すとき,
位置が重なるかけ算の組み合わせは,
「\( 1 \times 1 \)」と「\( 8 \times 1 \)」,「\( 2 \times 1 \)」と「\( 7 \times 1 \)」,
「\( 3 \times 1 \)」と「\( 6 \times 1 \)」,「\( 4 \times 1 \)」と「\( 5 \times 1 \)」
になります。
それぞれの組み合わせにおいて,かけられる数に注目すると,
「\( 1 \)」と「\( 8 \)」,「\( 2 \)」と「\( 7 \)」,
「\( 3 \)」と「\( 6 \)」,「\( 4 \)」と「\( 5 \)」
であり,それぞれの和は \( 9 \) になっています。
よって,あるかけ算のかけられる数を \( a \) とするとき,
そこに重なるかけ算のかけられる数は \( 9-a \) になります。
Q
かけられる数を \( 1 \) に固定して,図2のように折り返すとき,
位置が重なるかけ算の組み合わせは,
「\( 1 \times 1 \)」と「\( 1 \times 8 \)」,「\( 1 \times 2 \)」と「\( 1 \times 7 \)」,
「\( 1 \times 3 \)」と「\( 1 \times 6 \)」,「\( 1 \times 4 \)」と「\( 1 \times 5 \)」
になります。
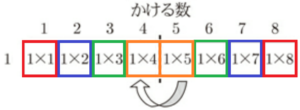
それぞれの組み合わせの,かける数に注目すると,
「\( 1 \)」と「\( 8 \)」,「\( 2 \)」と「\( 7 \)」,
「\( 3 \)」と「\( 6 \)」,「\( 4 \)」と「\( 5 \)」
であり,それぞれの和は \( 9 \) になっています。
よって,あるかけ算のかける数を \( b \) とするとき,
そこに重なるかけ算のかけられる数は \( 9-b \) になります。
イ 会話文中の R にあてはまる偶数を求めよ。
【解説】
問アをヒントにして \( a \times b \) と重なる4つのかけ算の和を実際に求めてみると,
\( (a \times b)+\{ (9-a) \times b \}+\{ a \times (9-b) \}+\{ (9-a) \times (9-b) \} \)
\( =ab+(9b-ab)+(9a-ab)+(81-9a-9b+ab) \)
\( =81(=9^2) \)
であり,文字 \( a,b \) を含む項はすべて消え,\( 9^2 \) の部分だけが残ります。
この \( 9 \) は \( 1+8 \) で,「 \( 1 \) から \( 8 \) まで書かれているとき」の
\( 1 \) と \( 8 \) の和になっています。
このことから, R にあてはまる偶数を \( n \) とすると,
和が \( 2025 \) になるとき,
\( (1+n)^2=2025 \)
\( (1+n)^2=45^2 \) (\( n>1 \) より \( 1+n>2 \))
\( 1+n=45 \)
\( n=44 \)
(2) 太郎さんが店長をしている店には,\( 1000 \) 円札と \( 500 \) 円玉専用の両替機が1台設置されている。この両替機に \( 1000 \) 円札を \( 1 \) 枚投入すれば,\( 500 \) 円玉 \( 1 \) 枚と \( 100 \) 円玉 \( 5 \) 枚が出てくる。また,この両替機に \( 500 \) 円玉を \( 1 \) 枚投入すれば,\( 100 \) 円玉 \( 4 \) 枚と \( 50 \) 円玉 \( 2 \) 枚が出てくる。
1月31日の営業終了後すぐに,太郎さんが,両替機の中にある紙幣と硬貨の枚数を確認すると,この日の営業開始前に比べて,\( 50 \) 円玉の枚数が \( 12 \) 枚減っていた。
2月1日の営業開始前に,太郎さんは,両替機の中にある紙幣と硬貨の枚数を,\( 1000 \) 円札 \( 0 \) 枚,\( 500 \) 円玉 \( 30 \) 枚,\( 100 \) 円玉 \( 200 \) 枚,\( 50 \) 円玉 \( 50 \) 枚にして,店の営業を開始した。そして,2月1日の営業終了後すぐに,両替機の中にある紙幣と硬貨の枚数を確認した。
1月31日と2月1日の営業時間内に,両替機の中の硬貨の枚数が不足して両替ができなくなることはなかった。
これについて,次のア~ウの問いに答えよ。
ア 1月31日の営業時間内に,両替機に投入された \( 500 \) 円玉の枚数は何枚か。
【解説】
\( 500 \) 円玉を \( 1 \) 枚投入すれば,\( 100 \) 円玉 \( 4 \) 枚と \( 50 \) 円玉 \( 2 \) 枚が出てくる
ということは,\( 500 \) 円玉が \( 1 \) 枚投入されると,\( 50 \) 円玉は \( 2 \) 枚減ります。
よって,\( 50 \) 円玉の枚数が \( 12 \) 枚減ったということは,
投入された \( 500 \) 円玉の枚数は,
\( 12 \div 2=6 \)(枚)
イ 2月1日の営業終了後の両替機の中にあった \( 100 \) 円玉の枚数は何枚か。2月1日の営業時間内に,両替機に投入された \( 1000 \) 円札の枚数を \( x \) 枚,\( 500 \) 円玉の枚数を \( y \) 枚として,\( x \) と \( y \) を使った式で表せ。
【解説】
\( 1000 \) 円札が \( 1 \) 枚投入されると,\( 100 \) 円玉は \( 5 \) 枚減るので,
\( 1000 \) 円札が \( x \) 枚投入されると,\( 100 \) 円玉は \( 5x \) 枚減ります。
\( 500 \) 円玉が \( 1 \) 枚投入されると,\( 100 \) 円玉は \( 4 \) 枚減るので,
\( 500 \) 円玉が \( y \) 枚投入されると,\( 100 \) 円玉は \( 4y \) 枚減ります。
2月1日の営業開始前には,両替機の中に \( 100 \) 円玉が \( 200 \) 枚入っていたので,
営業終了後の \( 100 \) 円玉の枚数は,\( (200-5x-4y) \) 枚になります。
ウ 2月1日の営業終了後の両替機の中にあった,\( 500 \) 円玉の枚数は \( 24 \) 枚で,\( 100 \) 円玉の枚数は \( 50 \) 円玉の枚数より \( 15 \) 枚多かった。このとき,2月1日の営業時間内に両替機に投入された \( 1000 \) 円札と \( 500 \) 円玉の枚数はそれぞれ何枚か。2月1日の営業時間内に両替機に投入された \( 1000 \) 円札の枚数を \( x \) 枚,\( 500 \) 円玉の枚数を \( y \) 枚として,\( x,y \) の値を求めよ。\( x,y \) の値を求める過程も,式と計算を含めて書け。
【解答】
2月1日の営業終了後の両替機の中にあった \( 500 \) 円玉,\( 100 \) 円玉,\( 50 \) 円玉の枚数を
\( x,y \) を使って表すと,
\( 500 \) 円玉の枚数は \( (30-x+y) \) 枚
\( 100 \) 円玉の枚数は \( (200-5x-4y) \) 枚
\( 50 \) 円玉の枚数は \( (50-2y) \) 枚
と表すことができる。
2月1日の営業終了後の両替機の中にあった,
\( 500 \) 円玉の枚数は \( 24 \) 枚なので,
\( 30-x+y=24 \) ・・・ ➀
2月1日の営業終了後の両替機の中にあった,
\( 100 \) 円玉の枚数は \( 50 \) 円玉の枚数より \( 15 \) 枚多かったので,
\( 200-5x-4y=(50-2y)+15 \) ・・・ ➁
➀➁を連立方程式として解くと,
\( x=21,y=15 \)
よって,2月1日の営業時間内に両替機に投入された
\( 1000 \) 円札の枚数は \( 21 \) 枚
\( 500 \) 円玉の枚数は \( 15 \) 枚
【解説】
連立方程式の途中式
\( \left\{ \begin{array}{}
30-x+y=24 \;\; ・・・ \;\; ➀ \\
200-5x+4y=(50-2y)+15 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀を整理すると
\( -x+y=-6 \) ・・・ ➀’
➀’ \( \times 2 \) すると
\( -2x+2y=-12 \) ・・・ ➀”
➁を整理すると
\( 200-5x-4y=(50-2y)+15 \)
\( -5x-2y=-135 \) ・・・ ➁’
➀” \( – \) ➁’すると
\( -7x=-147 \)
\( x=21 \)
➀’に代入すると,
\( -21+y=-6 \)
\( y=15 \)
大問5
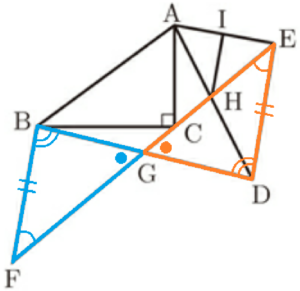
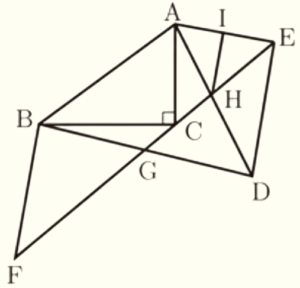
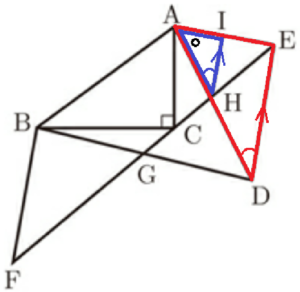
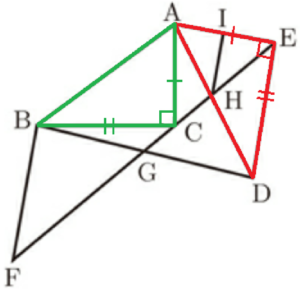
右の図のような,\( △ABC \) と \( △ADE \) がある。\( △ABC \) は,\( ∠ACB=90° \) の直角三角形であり,\( △ADE \) は,\( △ABC \) を点 \( A \) を回転の中心として,回転移動したものである。2点 \( C,E \) は異なる点であり,直線 \( AB \) について同じ側にある。直線 \( CE \) 上に,点 \( C \) と異なる点 \( F \) を,\( BC=BF \) となるようにとる。直線 \( BD \) と直線 \( EF \) との交点を \( G \) とする。また,直線 \( AD \) と直線 \( CE \) との交点を \( H \) とする。点 \( H \) を通り,辺 \( DE \) に平行な直線をひき,直線 \( AE \) との交点を \( I \) とする。
このとき,次の(1),(2)の問いに答えなさい。
(1) \( △ADE \) ∽ \( △AHI \) であることを証明せよ。
【解答】
\( △ADE \) と \( △AHI \) において
共通な角なので,
\( ∠DAE=∠HAI \) ・・・ ➀
平行な2直線の同位角は等しいので,
\( ∠ADE=∠AHI \) ・・・ ➁
➀➁より,
2組の角がそれぞれ等しいので,
\( △ADE \) ∽ \( △AHI \)
(2) \( △DEG≡△BFG \) であることを証明せよ。
【解答】
\( △DEG \) と \( △BFG \) において,
\( △ADE \) は,\( △ABC \) を点 \( A \) を回転の中心として,回転移動したものなので,
\( DE=BC \) ・・・ ➀
\( AE=AC \) ・・・ ➁
\( ∠AED=∠ACB=90° \) ・・・ ➂
仮定より,
\( BC=BF \) ・・・ ➃
➀➃より,
\( DE=BF \) ・・・ ➄
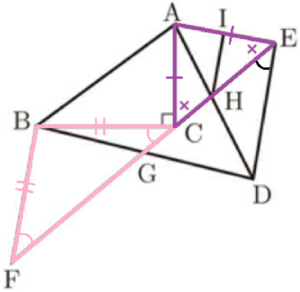
➁より,\( △ACE \) は二等辺三角形なので,
\( ∠ACE=∠AEC \) ・・・ ⑥
➂より,
\( ∠DEG=90°-∠AEC \) ・・・ ➆
3点 \( E,C,F \) は一直線上の点なので,
\( ∠BCF=90°-∠ACE \) ・・・ ⑧
⑥➆➇より,
\( ∠DEG=∠BCF \) ・・・ ➈
➃より,\( △BCF \) は二等辺三角形なので,
\( ∠BFG=∠BCF \) ・・・ ⑩
➈➉より,
\( ∠DEG=∠BFG \) ・・・ ⑪
対頂角は等しいので,
\( ∠DGE=∠BGF \) ・・・ ⑫
三角形の内角は \( 180° \) なので,
\( ∠GDE=180°-(∠DEG+∠DGE) \) ・・・ ⑬
\( ∠GBF=180°-(∠BFG+∠BGF) \) ・・・ ⑭
⑪⑫⑬⑭より,
\( ∠GDE=∠GBF \) ・・・ ⑮
➄⑪⑮より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △DEG≡△BFG \)
➀➁➂
⑥~⑪
1組の辺とその両端の角がそれぞれ等しい