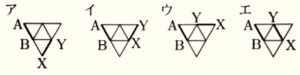大問1
問1 \( 2+12 \div (-3) \) を計算しなさい。
【解答】
\( 2+12 \div (-3) = 2+(-4) \)
\( = -2 \)
問2 \( \sqrt{20}+\dfrac{10}{ \sqrt{5}} \) を計算しなさい。
【解答】
\( \sqrt{20}+\cfrac{10}{ \sqrt{5}} = 2\sqrt{5}+\cfrac{10 \times \sqrt{5}}{ \sqrt{5} \times \sqrt{5}} \)
\( = 2\sqrt{5}+\cfrac{10\sqrt{5}}{5} \)
\( = 2\sqrt{5}+2\sqrt{5} \)
\( = 4\sqrt{5} \)
問3 方程式 \( x^2+x-4 \) を解きなさい。
【解答】
\( x^2+x-4 = \dfrac{ -1±\sqrt{1^2-4 \times 1 \times (-4)} }{ 2 \times 1 } \)
\( = \dfrac{ -1±\sqrt{17}}{ 2 } \)
問4
1本 \( a \) 円の鉛筆5本と,1本 \( b \) 円のボールペン3本の代金の合計は,1000円より高い。
この数量の関係を不等式で表しなさい。
【解答】
「1本 \( a \) 円の鉛筆5本の代金」を文字式で表すと → \( 5a \)
「1本 \( b \) 円のボールペン3本の代金」を文字式で表すと → \( 3b \)
この合計が1000円 ”より高い” ので,\( 5a+3b>1000 \)
問5
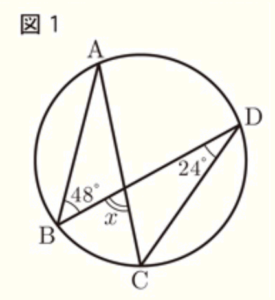
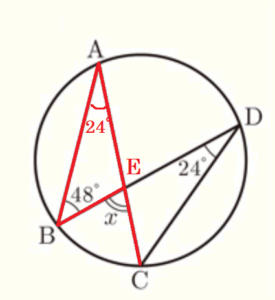
図1のように,円周上に4点 \( A,B,C,D \) をとる。このとき,∠\( x \)の大きさを求めなさい。
【解答】
線分 \(AC\) と線分 \( BD \) の交点を \(E\) とすると,
円周角は等しいので \( ∠BAC=∠BDC=24° \)
\( ∠ x \) は \( △ABE \) の外角なので,
\( ∠ x = ∠BAC+∠ABD= 24°+48°=72° \)
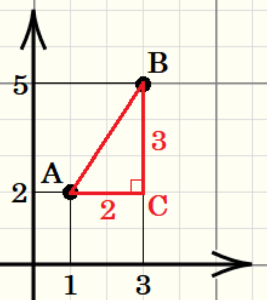
問6 2点 \( A(1,2),B(3,5) \) の間の距離を求めなさい。
【解答】
点 \( A \) を通り\( x \) 軸に平行な直線と点 \( B \) を通り \( y \) 軸に平行な直線の交点を \( C \) とすると,
\(△ABC\) は直角三角形になっているので,
\( AB^2 = AC^2+BC^2 \)
\( = 2^2+3^2 \)
\( = 13 \)
\( AB= \sqrt{13} \) \( (AB>0より) \)
問7 次のア~エのうち,\( y \) が \( x \) に反比例するものを1つ選び,記号で答えなさい。
ア 半径が \( x \; cm \) である円の周の長さ \( y \; cm \)
イ 半径が \( x \; cm \) である円の面積 \( y \; cm^2 \)
ウ 周の長さが \( 20 \; cm \) である長方形の縦の長さ \( x \; cm \) と横の長さ \( y \; cm \)
エ 面積が \( 20 \; cm^2 \) である長方形の縦の長さ \( x \; cm \) と横の長さ \( y \; cm \)
【解答】
反比例を表す式は \( y=\dfrac{a}{x} \) (\( a \) は定数) です。
ア~エそれぞれの関係を \( x,y \) を使って表すと,
ア \( y=2\pi{}x \)
イ \( y=\pi{}x^2 \)
ウ \( 2(x+y)=20 → y=-x+10 \)
エ \( xy=20 → y=\dfrac{20}{x} \)
よって,答えは エ
問8
みなみさんの通う中学校では冬休みが20日あり,数学の宿題が70問出題されている。みなみさんは1日あたり3問か5問を毎日解いて,20日目にちょうど宿題が終わる計画を立てた。3問解く日と5問解く日はそれぞれ何日か,求めなさい。
【解答】
3問解く日を \( x \) 日,5問解く日を \( y \) 日とすると,
\( 3x+5y=70 \) ・・・ ➀
\( x+y=20 \) ・・・ ➁
➁ × 3
\( 3x+3y=60 \) ・・・ ➁’
➀-➁’
\( 2y=10 \)
\( y=5 \)
➁ に代入
\( x+5=20 \)
\( x=15 \)
よって,3問解く日が15日,5問解く日が5日
問9
図2は,ある月のカレンダーである。カレンダーの8日から24日のうち,月曜日から金曜日までの数から1つを選び〇で囲む。○で囲んだ数を \( n \) とし,\( n \) の真上の数を \( a \),真下の数を \( b \),左横の数を \( c \),右横の数を \( d \) とする。例えば,図2のように 14 を○で囲むと,\( n=14 \),\( a=7 \),\( b=21 \),\( c=13 \),\( d=15 \) となる。下の1,2に答えなさい。
1 \( a \) を \( n \) を使って表しなさい。
2 \( a \),\( b \),\( c \),\( d \) をそれぞれ \( n \) を使って表し,\( bc-ad \) を計算すると,\( bc-ad \) はどのような数になるか。次のア~エから最も適当なものを1つ選び,記号で答えなさい。
ア 12の倍数 イ 奇数 ウ 24の倍数 エ 負の数
【解答】
\( a \),\( b \),\( c \),\( d \) をそれぞれ \( n \) を使って表すと,
\( a=n-7,b=n+7,c=n-1,d=n+1 \) となるので,
\( bc-ad=(n+7)(n-1)-(n-7)(n+1) \)
\( =(n^2+6n-7)-(n^2-6n-7) \)
\( =12n \)
よって,答えは ア 12の倍数
大問2
問1
赤球3個と白球1個がはいっている袋から球を取り出すとき,次の1~3に答えなさい。
ただし,1~3のそれぞれについて,どの球が取り出されることも同様に確からしいものとする。
1 袋から球を1個取り出すとき,赤球が出る確率を求めなさい。
【解答】
はいっている球の総数は4個で,そのうち,赤球は3個なので,赤球が出る確率は \(\dfrac{3}{4}\)
2 袋から球を1個ずつ2回続けて取り出すとき,2個とも赤球が出る確率を求めなさい。
【解答】
樹形図を書いてみます。
球の取り出し方の総数は12通りで,そのうち,2個とも赤球になるのは6通り。よって,2個とも赤球が出る確率は \(\cfrac{6}{12}=\cfrac{1}{2}\)

3 袋から球を1個取り出して色を調べ,それを袋にもどしてから,また,球を1個取り出す。このとき,2個とも赤球が出る確率を求めなさい。
【解答】
樹形図を書いてみます。球の取り出し方の総数は16通りで,そのうち,2個とも赤球になるのは9通り。よって,2個とも赤球が出る確率は \(\dfrac{9}{16}\)
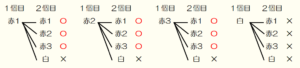
問2 あみさんとけいすけさんは,正四面体について話し合っている。次の1,2に答えなさい。
1 あみさんは正四面体の展開図を考えた。次のア~エの展開図を組み立てて正四面体をつくるとき,辺 \( AB \) と辺 \( XY \) がねじれの位置になる展開図はどれか,ア~エから1つ選び,記号で答えなさい。
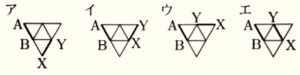
【解答】
展開図の赤で塗った面を底面として正四面体を組み立ててみます。
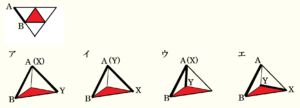
ねじれの位置になるのは エ になります。
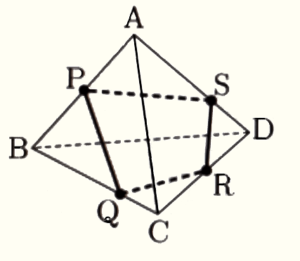
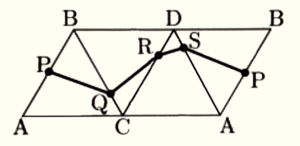
2 図1のような,正四面体 \( ABCD \) がある。ひもを辺 \( AB \) の中点 \( P \) から,正四面体の辺 \( BC,CD,DA \) を順に通るように点 \( P \) まで1周させる。ひもが辺 \( BC,CD,DA \) 上を通る点をそれぞれ点 \( Q,R,S \) とする。2人は,ひもの長さが最小となる場合について考えている。下の会話文の (Ⅰ) に適する言葉を入れ、 (Ⅱ) にあてはまる言葉をあとの選択肢ア~ウから1つ選び,記号で答えなさい。
-- 以下,会話文 ----------------------
けいすけ
正四面体の展開図は,1であみさんが考えたもの以外にも,図2のように平行四辺形になるものもあるね。
あみ
ひもの長さ \( (PQ+QR+RS+SP) \) が最小となるときを図2の展開図で考えると,点 \( P,Q,R,S \) が (Ⅰ) ときだね。
けいすけ
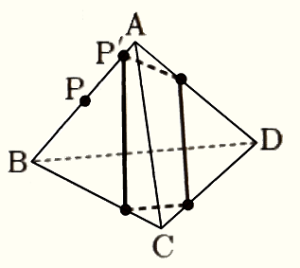
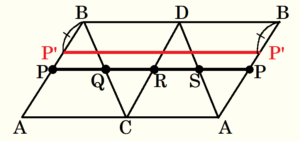
図3のように,辺 \( AB \) 上で点 \( P \) 以外の点 \( P’ \) から,同じように正四面体の辺 \( BC,CD,DA \) を順に通るようにひもを点 \( P’ \) まで1周させたときは,最小となるひもの長さはどうなるかな。
あみ
点 \( P’ \) から1周させたときの最小となるひもの長さは,点 \( P \) から1周させたときの最小となるひもの長さと比べると (Ⅱ) よ。
-- 以上,会話文 ----------------------
(Ⅱ) の選択肢
ア 短くなる イ 同じになる ウ 長くなる
【解答】
(Ⅰ)
2点間を最短で結ぶのは,直線で繋いだ時です。つまり,点 \( P,Q,R,S \) が 一直線上に並ぶときになります。 (Ⅱ)
点 \( P’ \) がどの位置にあっても左右の \( BP’ \) の長さは等しいので, \( P’P’//BB \) になります。よって,四角形 \( BP’P’B \) は平行四辺形になるので, 点 \( P’ \) がどの位置にあっても長さは同じになります。
大問3
問1
かいとさんは. 自転車を10000円以下で購入したいと考えている。図1はA店,B店,C店,D店の自転車価格の分布のようすを箱ひげ図に表したものである。ただし、どの店にも自転車は50台あるとする。下の1,2に答えなさい。
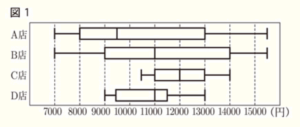
1 次の(1),(2)に答えなさい。
(1) A店の第一四分位数を求めなさい。
(2) 図1の箱ひげ図から読みとれることとして正しいと判断できるものを,次のア~エから2つ選び,記号で答えなさい。
ア A店にある8000円以上13000円以下の自転車の台数は20台である。
イ B店には9000円の自転車がかならずある。
ウ C店には10000円以下の自転車はない。
エ D店の自転車価格の平均値は11000円である。
【解答】
ア 第一四分位数8000円にあたるのは,安い方から13番目,
第三四分位数13000円にあたるのは,安い方から38番目。
8000円以上13000円以下の自転車は,26台以上あるので,正しくない。
イ B店の第一四分位数は9000円なので,安い方から13番目の自転車が9000円
であり,正しい。
ウ C店の最小値は10000円より大きいので,正しい。
エ 箱ひげ図だけの情報から平均値は求められないので,正しくない。
よって,正しいのは,イ,ウ
2 かいとさんは,A店,B店の自転車価格を図1の箱ひげ図と,2店のヒストグラムで比べることにした。 図2の ➀,➁ はA店,B店どちらかの自転車価格をヒストグラムに表したものである。あとの(1) ,(2)に答えなさい。
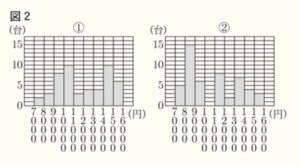
(1) 図2の ➀ について,9000円以上10000円未満の階級の相対度数を求めなさい。
【解答】
9000円以上10000円未満の階級の度数は8,データの総数は50なので,
相対度数は,\( \dfrac{8}{50}=0.16 \)
(2) 図2の ➀,➁ のうち,9000円以上10000円未満の自転車が多くある店のヒストグラムはどちらか。また,A店のヒストグラムはどちらか。その組み合わせとして正しいものを,次のア~エから1つ選び,記号で答えなさい。

【解答】
9000円以上10000円未満の階級の度数は,➀が 8 ,➁が 6 なので,
9000円以上10000円未満の階級の度数が多いのは ➀。
図1から,A店の第一四分位数は8000円で,安い方から13番目。
これにあてはまるのは ➁。
よって,答えは イ 。
問2
かいとさんは自転車をこいだときの自転車の速さと,その速さで1時間こいだときに消費するエネルギーについて考えた。表は,かいとさんのこぐ自転車の速さと1時間に消費するエネルギーをまとめたものである。自転車の速さを \( x \; km/h \),1時間に消費するエネルギーを \( y \; kcal \) とし,\( 0≦x≦40 \) のとき \( y \) を \( x \) の一次関数とみなして考える。ただし,人は動かなくてもエネルギーを消費するため,\( 0 \; km/h \) でも消費するエネルギーは \( 0 \; kcal \) にはならない。下の1~3に答えなさい。

1 \( x \) と \( y \) の関係を表すグラフを図3にかき入れなさい。
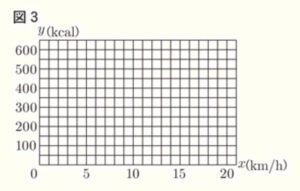
【解答】
2点 \( (5,200),(20,500) \) を通る直線になります。
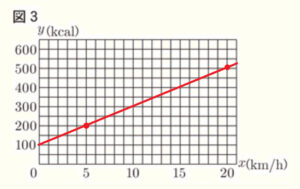
2 \(y\) を \(x\) の式で表しなさい。ただし,変域は求めなくてよい。
【解答】
傾き= \( \dfrac{yの変化量}{xの変化量} \) で求めることができるので,
2点 \( (5,200),(20,500) \) を通る場合,
傾き= \( \dfrac{500-200}{20-5}=20 \)
求める式を \(y=20x+b\) として, \( x=5,y=200 \) を代入すると,
\( 200=20 \times 5+b \)
\(b=100\)
よって,求める式は,\(y=20x+100\)
3 かいとさんが食べたお弁当のエネルギーは \( 740 kcal \) だった。かいとさんが,自転車をちょうど1時間こいで,このエネルギーをすべて消費するためには,自転車の速さを何 \( km/h \) にすればよいか,求めなさい。
【解答】
\(y=20x+100\) に \(y=740\) を代入すると,
\(740=20x+100\)
\(20x=640\)
\(x=32 \; (km/h) \)
大問4
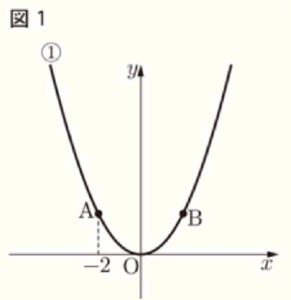
図1のように関数 \( y=\dfrac{1}{2}x^2 \) ・・・ ① のグラフ上に,
2点 \( A,B \) を \( y \) 軸について対称となるようにとる。
点 \( A \) の \( x \) 座標が \( -2 \) のとき,下の問1~問3に答えなさい。
問1 線分 \( AB \) の長さを求めなさい。
【解答】
2点 \( A,B\) が \( y \) 軸について対称な点ということは,
\( A \) と \( B \) の \( x \) 座標の絶対値が等しいので,\( B \) の \( x \) 座標は \( 2 \) 。
よって,線分 \( AB \) の長さは,\( 2-(-2)=4 \) 。
問2 関数 ①について,次の1,2に答えなさい。
1 次のア~ウのうち,変化の割合が最も大きいものを1つ選び,記号で答えなさい。
ア \( x \) の値が \( 0 \) から \( 2 \) まで増加するとき
イ \( x \) の値が \( 2 \) から \( 4 \) まで増加するとき
ウ \( x \) の値が \( 4 \) から \( 6 \) まで増加するとき
【解答】
関数 \( y=ax^2 (a>0) \) では,\( x \) の絶対値が大きくなるほど変化の割合が大きくなります。
よって,変化の割合が最も大きいのは,ウ 。
2 \( x \) の変域が \( -3≦x≦2 \) のときの \( y \) の変域を求めなさい。
【解答】
関数 \( y=ax^2 (a>0) \) のグラフでは,
\( x \) の変域が \( 0 \) をはさむとき,\( y \) の最小値は \( 0 \) になります。
また,\( y \) の値は,\( x \) の絶対値が大きいほど大きくなるので,
\( x \) の変域が \( -3≦x≦2 \) のとき,\( y \) が最大値をとるのは,\( x=-3 \) のとき。
\( x=-3 \) のときの \( y \) の値は,
\( y=\dfrac{1}{2} \times (-3)^2=\dfrac{9}{2} \)
よって,\( y \) の変域は, \( 0≦y≦\dfrac{9}{2} \)
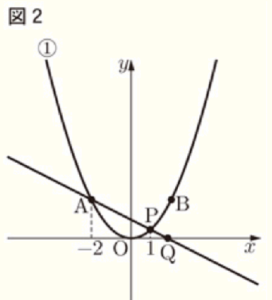
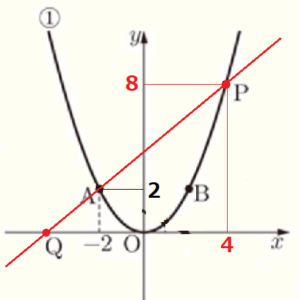
問3 図1において,関数 ① のグラフ上に点 \( P \) をとり,直線 \( AP \) が \( x \) 軸と交わる点を \( Q \) とする。ただし、点 \( P \) は2点 \( A,B\) とは異なる点とする。次の1~3に答えなさい。
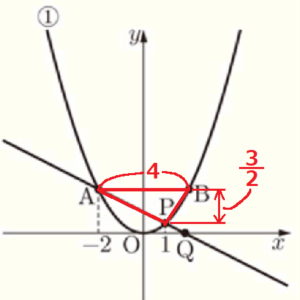
1 図2のように,点 \( P \) の \( x \) 座標が 1 であるとき, \( △APB \) の面積を求めなさい。
【解答】
\( A (-2,2) ,B(2,2),P \left(1,\dfrac{1}{2} \right) \) なので,
\( △APB=4 \times \dfrac{3}{2} \times \dfrac{1}{2}=3 \)
2 点 \( P \) の \( x \) 座標が 4 であるとき,次の(1) ,(2)に答えなさい。
(1) 直線 \( AP \) の傾きを求めなさい。
【解答】
\( A(-2,2),P(4,8) \) なので,
傾き= \( \dfrac{8-2}{4-(-2)}=1 \)
(2) 点 \( Q \) の座標を求めなさい。
【解答】
直線 \( AP \) の式を \( y=x+b \) とし,\( x=4,y=8 \) を代入すると,
\( 8=4+b \)
\( b=4 \)
となり,直線 \( AP \) の式は,\( y=x+4 \)
\( y=0 \) を代入すると,
\( 0=x+4 \)
\( x=-4 \)
よって,\( Q(-4,0) \)
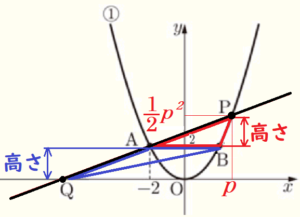
3 点 \( P \) の \( x \) 座標を \( p \) とする。\( p \) が正の数であるとき,\( △APB \) の面積が \( △AQB \) の面積の \( \dfrac{1}{2} \) 倍となる \( p \) の値をすべて求めなさい。
【解答】
\( △APB \) と \( △AQB \) の辺 \( AB \) を底辺と考えると,\( △APB \) の高さが \( △AQB \) の高さの \( \dfrac{1}{2} \) 倍であるとき,\( △APB \) の面積は \( △AQB \) の面積の \( \dfrac{1}{2} \) 倍になります。 2点 \( A,B \) の \( y \) 座標が 2 なので,\( △AQB \) の高さは 2 です。
よって,,\( △APB \) の高さが 1 であればいいことになります。\( P\left(p,\dfrac{1}{2}p^2\right) \) なので,\( \dfrac{1}{2}p^2=3 \) の場合と \( \dfrac{1}{2}p^2=1 \)の場合を考えます。
● \( \dfrac{1}{2}p^2=3 \) の場合
\( \dfrac{1}{2}p^2=3 \)
\( p^2=6 \)
\( p= \sqrt{6} ( p>0より ) \)
● \( \dfrac{1}{2}p^2=1 \) の場合
\( \dfrac{1}{2}p^2=1 \)
\( p^2=2 \)
\( p= \sqrt{2} ( p>0より) \)
よって,あてはまる \( p \) の値は,\( p=\sqrt{2},\sqrt{6} \)
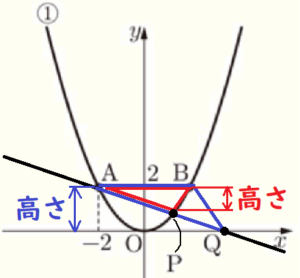
注
この問題では,点 \( P \) が辺 \( AB \) の上側にあるときと下側にあるときの2パターンあることに注意しましょう。
大問5
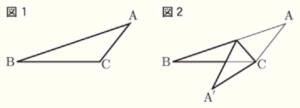
図1のような \( △ABC \) の紙があり,図2のように辺 \( AB \) 上の点と点 \( C \) を結んだ線分を折り目として \( △ABC \) を折る。点 \( A \) について,折る前の点を \( A \) ,折って移った点を \( A’ \) とするとき,下の問1~問3に答えなさい。
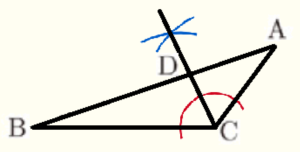
問1 図3のように,辺 \( AC \) が辺 \( BC \) に重なるように \( △ABC \) を折る。折り目となる線分を \( CD \) とするとき,下の1,2に答えなさい。
1 \( △ACD \) と合同な三角形を答えなさい。
【解答】
折り返す前と後の図形が合同なので,\( △ACD \) と合同なのは \( △A’CD \)
2 図1に,折り目となる線分 \( CD \) を、定規とコンパスを用いて作図しなさい。
ただし、作図に用いた線は消さないでおくこと。
【解答】
手順1 点 \( C \) を中心に線分 \( BC,AC \) と交わるように
弧を描く
手順2 手順1の弧と線分 \( BC \) の交点を中心に弧を描く
手順3 手順1の弧と線分 \( AC \) の交点を中心に手順2と
同じ半径の弧を描く
手順4 手順2と3の弧の交点と点 \( C \) を結ぶ半直線を描く
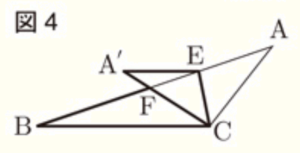
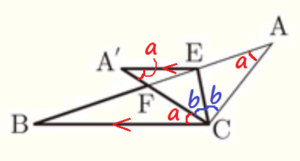
問2 図4のように,辺 \( AB \) 上に点 \( E \) をとり,線分 \( CE \) を折り目として \( △AEC \) を折り返すと,\( A’E//BC \) となった。線分 \( A’C \) と線分 \( BE \) との交点を \( F \) とするとき,下の1~3に答えなさい。
1 \( △A’FE \) ∽ \( △CFB \) であることを証明しなさい。
【解答】
\( A’E//BC \) より錯角は等しいので,
\( ∠A’EF=∠CBF \) ・・・ ➀
\( ∠EA’F=∠BCF \) ・・・ ➁
➀➁より,2組の角の大きさが等しいので,\( △A’FE \) ∽ \( △CFB \)
2 \( ∠CAE=∠a \) ,\( ∠ACE=∠b \)とするとき,\( ∠a+∠b \) で表される角を2つ答えなさい。
【解答】
1個目
\( △ACE \) において内角と外角の関係から,
\( ∠CEB = ∠CAE + ∠ACE \)
\( =∠a+∠b \)
2個目
\( △ACE≡△A’CE \) なので,
\( ∠EA’C = ∠EAC = ∠a \)
\( ∠A’CE = ∠ACE = ∠b \)
\( A’E//BC \) より錯角は等しいので,
\( ∠BCA’ = ∠EA’C = ∠a \)
\( ∠BCE = ∠BCA’ + ∠A’CE = ∠a+∠b \)
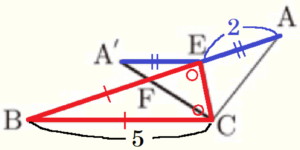
3 \( AB=7,BC=5 \) であるとき,線分 \( EF \) の長さを求めなさい。
【解答】
(2)より,\( ∠CEB=∠BCE=∠a + ∠b \) なので,
\( △BCE \) は \( BE=BC \) の二等辺三角形であり,
\( BE=BC=5 \)
\( AE=AB-AE=2 \)
\( △A’CE≡△ACE \) なので,
\( A’E=AE=2 \)
(1)より \( △A’FE \) ∽ \( △CFB \) であり,
相似比は \( BC:EA’=5:2 \)
よって,\( EF=\dfrac{2}{7}BE=\dfrac{10}{7} \)
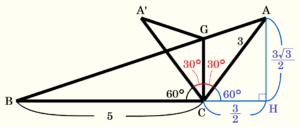
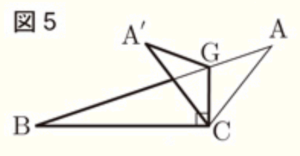
問3 図5のように,点 \( C \) を通り辺 \( BC \) に垂直な直線と辺 \( AB \) との交点を \( G \) とする。線分 \( CG \) を折り目として \( △AGC \) を折り返す。 \( BC=5,CA=3,∠A’CB=60° \) であるとき,線分 \( CG \) の長さを求めなさい。
【解答】
\( GC⊥BC,∠A’CB=60° \) より,\( ∠A’CG=30° \)
\( △AGC≡△A’GC \) なので, \( ∠ACG=∠A’CG=30° \)
\( BC \) の延長線に対して点 \( A \) から垂線をひき,交点を \( H \) とすると,
\( ∠ACH=180°-(∠A’CB+∠A’CG+∠ACG)=60° \)
\( △ACH \) は \( 30°,60°,90° \) の直角三角形なので,
\( AC:AH=2:\sqrt{3} \) より,\( AH=\dfrac{3\sqrt{3}}{2} \)
\( AC:CH=2:1 \)より,\( CH=\dfrac{3}{2} \)
\( △BCG \) ∽ \( △BHA \) なので,
\( CG:HA=BC:BH \)
\( CG:\dfrac{3\sqrt{3}}{2}=5:\left(5+\dfrac{3}{2}\right) \)
\( \dfrac{13}{2}CG=\dfrac{15\sqrt{3}}{2} \)
\( CG=\dfrac{15\sqrt{3}}{13} \)