大問1
(1) \( 4-7 \) を計算しなさい。
(2) \( 2x-(3x-y) \) を計算しなさい。
(3) \( (\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2}) \) を計算しなさい。
【解説】
\( =(\sqrt{6})^2-(\sqrt{2}^2) \)
\( =6-2 \)
\( =4 \)
(4) \( x^2+10x+24 \) を因数分解しなさい。
(5) 2次方程式 \( x^2-5x+5=0 \) を解きなさい。
【解答】
\( x=\dfrac{5±\sqrt{5}}{2} \)
【解説】
\( ax^2+bx+c=0 \) とすると,\( a=1,b=-5,c=5 \) なので,
解の公式より,
\( x=\dfrac{-b±\sqrt{b^2-4ac}}{2a} \)
\( =\dfrac{-(-5)±\sqrt{(-5)^2-4 \times 1 \times 5}}{2 \times 1} \)
\( =\dfrac{5±\sqrt{5}}{2} \)
大問2
周の長さが \( 4a \; cm \) の正方形があります。このとき,正方形の面積を,文字を使った式で表しなさい。
【解説】
周の長さが \( 4a \; cm \) なので,1辺の長さは,\( a \; cm \)
1辺の長さが \( a \; cm \) の正方形の面積は,\( a^2 \; cm^2 \)
大問3
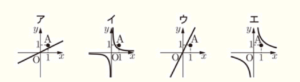
次の ア〜エ は,\( y=ax \) のグラフまたは \( y=\dfrac{a}{x} \) のグラフと,点 \( A(1,1) \) を表したものです。ア〜エ のうち,\( y=\dfrac{a}{x} \) の \( a \) の値が \( 1 \) より大きいグラフを表しているものはどれですか。一つ選び,その記号を書きなさい。
【解説】
\( y=\dfrac{a}{x} \) は,反比例のグラフを表す式です。
ア〜
エ のうち,反比例のグラフは
イ,エ
\( y=\dfrac{a}{x} \) において,\( x=1 \) とすると,\( y=a \) になります。
イ,エ のうち,\( x=1 \) のときの \( y \) の値が \( 1 \) より大きいのは,エ
大問4
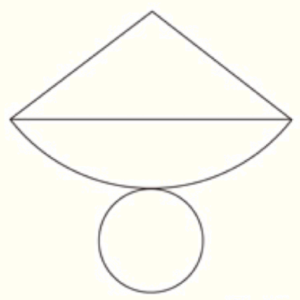
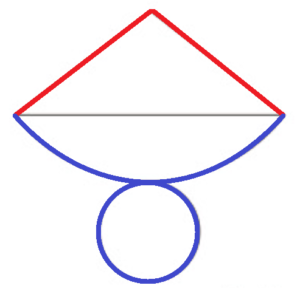
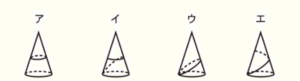
(1) 右の図のように,円錐の展開図で,側面になるおうぎ形の弧に対する弦をかき入れました。
次の ア〜エ のうち,この展開図を組み立てたときにできる円錐として正しいものはどれですか。一つ選び,その記号を書きなさい。
【解説】
側面になるおうぎ形の半径にあたる線分は,組み立てたときぴったりくっつくので,かき入れた弦の始点と終点は同じ点になります。
ア〜エ のうち,弦の始点と終点は同じ点になっているのは ア,ウ
また,この弦の始点と終点はおうぎ形の弧上の点です。
おうぎ形の弧は,底面の円周とぴったり重なるので,
ア,ウ のうち,弦の始点が底面の円周上にあるのは,ウ
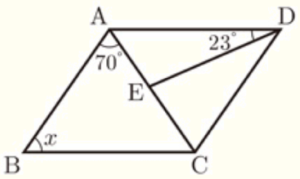
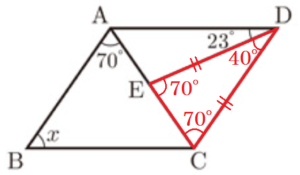
(2) 右の図で,四角形 \( ABCD \) は平行四辺形です。
\( DC=DE \) のとき,\( ∠x \) の大きさを求めなさい。
【解説】
平行四辺形の向かい合う辺は平行なので,\( AB//CD \)
錯角は等しいので, \( ∠BAC=∠DCE=70° \)
\( △DEC \) は \( DC=DE \) の二等辺三角形なので,
\( ∠DEC=∠DCE=70° \)
\( ∠CDE=180°-(∠DEC+∠DCE)=40° \)
\( ∠ADC=∠ADE+∠CDE=63° \)
平行四辺形の向かい合う角は等しいので,\( ∠x=∠ADC=63° \)
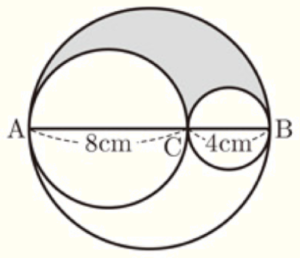
(3) 右の図は,線分 \( AB,AC,CB \) をそれぞれ直径として3つの円をかいたものです。
3つの円の弧で囲まれた色のついた部分の周の長さを求めなさい。
ただし,円周率は \( \pi{} \) とします。
【解説】
求める周の長さは,
・ 直径 \( 12 \; cm \) の半円の周
・ 直径 \( 8 \; cm \) の半円の周
・ 直径 \( 4 \; cm \) の半円の周
の合計になっています。
よって,
\( \dfrac{12\pi{}}{2}+\dfrac{8\pi{}}{2}+\dfrac{4\pi{}}{2} \)
\( =6\pi{}+4\pi{}+2\pi{} \)
\( =12\pi{} \; (cm) \)
大問5
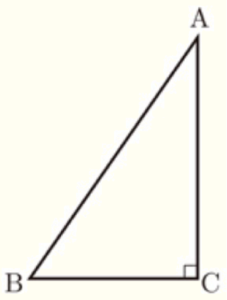
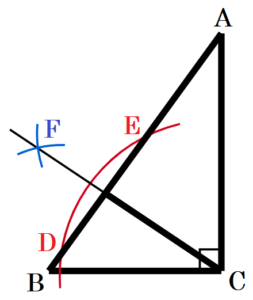
次の図の直角三角形 \( ABC \) で,辺 \( AB \) を底辺とするときの高さを表す線分を作図しなさい。
ただし,作図には定規とコンパスを用い,作図に使った線は消さないでおくこと。
【解答・解説】
点 \( A \) を通り,辺 \( AB \) に垂直な線分を描きます。
手順1 点 \( C \) を中心に辺 \( AB \) と交わる弧を描く。
(交点を \( D,E \) とします)
手順2 点 \( D,E \) を中心に同じ半径の弧を描く。
(交点を \( F \) とします)
手順3 点 \( C,F \) を通る直線を描く。
手順3の直線のうち,点 \( C \) から辺 \( AB \) までが
作図する線分になります。
大問6
あるクラスの生徒32人に対して,通学時間の調査を行いました。次の図は,通学時間の分布のようすを箱ひげ図に表したものです。
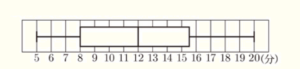
この箱ひげ図から,次のようなことを読み取ることができます。
【 通学時間が15分以上の生徒が8人以上いる。 】
このように読み取ることができるのはなぜですか。その理由を簡単に書きなさい。
ただし,理由には,次の語群から用語を1つ選んで用いること。
語群
【 第1四分位数 第2四分位数 第3四分位数 】
【解答・解説】
生徒数が32人なので,第3四分位数は通学時間が長い方から8番目と9番目の人の平均値になる。
箱ひげ図から,第3四分位数は,15分以上16分未満なので,
長い方から8番目の人の通学時間は15分以上である。
よって,通学時間が15分以上の生徒が8人以上いる。
大問7
AさんとBさんは,じゃんけんカードで遊んでいます。
グー,チョキ,パーの3種類のカードのうち何枚か持ち,これらを裏返してよくきったものから1枚ずつ出し合うことで,じゃんけんをします。
ただし,AさんとBさんが,それぞれどのカードを出すことも同様に確からしいものとします。
このとき,次の (1) ,(2) の問いに答えなさい。
(1) Aさんは2枚のカード,Bさんも2枚のカードを持っていて,それぞれ持っているカードから1枚だけ出し合います。Aさんのカードは,グーとチョキです。Bさんのカードは,グーとパーです。
このとき,AさんがBさんに勝つ確率を求めなさい。
【解説】
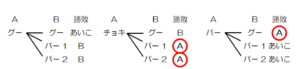
Aさん,Bさんが出したカードの組み合わせと勝敗を樹形図に書いてみます。
すべての場合の数は4通りで,Aさんが勝つのは1通りなので,
求める確率は,\( \dfrac{1}{4} \)

(2) Aさんは2枚のカード,Bさんは3枚のカードを持っていて,それぞれ持っているカードから1枚だけ出し合います。Bさんのカードは,グー,バー,バーです。
このとき,AさんがBさんに勝つ確率が \( \dfrac{1}{2} \) となるような,Aさんの2枚のカードの組み合わせを書きなさい。
【解説】
Aさん,Bさんが出したカードの組み合わせと勝敗を樹形図に書いてみます。
Aさんは2枚だけ持っているので,すべての場合の数は6通りになります。
Aさんが勝つ確率が \( \dfrac{1}{2} \) ということは,3通りなので,
あてはまるのは,チョキとパーの場合になります。
大問8
みずきさんは,お菓子屋さんでお土産を選んでいます。店員さんから,タルト4個とクッキー6枚で1770円のセットと,タルト7個とクッキー3枚で2085円のセットをすすめられました。
このとき,タルト1個とクッキー1枚の値段をそれぞれ求めなさい。
ただし,用いる文字が何を表すかを示して方程式をつくり,それを解く過程も書くこと。
なお,消費税は考えないものとします。
【解答】
タルト1個の値段を \( x \) 円,クッキー1枚の値段を \( y \) 円とし,
個数と代金の関係を連立方程式にすると,
\( \left\{
\begin{array}{}
4x+6y=1770 ・・・ ① \\
7x+3y=2085 ・・・ ➁
\end{array}
\right. \)
➁ \( \times \) 2
\( 14x+6y=4170 \) ・・・ ➁’
➁’ \(-\) ①
\( 10x=2400 \)
\( x=240 \)
➁に代入
\( 1680+3y=2085 \)
\( 3y=405 \)
\( y=135 \)
よって,タルト1個の値段は240円,クッキー1枚の値段は135円
大問9
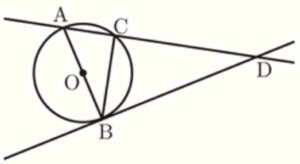
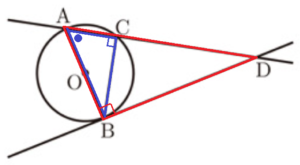
右の図のように,円 \( O \) の周上に異なる3点 \( A,B,C \) があり,線分 \( AB \) は円 \( O \) の直径となっています。点 \( B \) を通る円 \( O \) の接線をひき,直線 \( AC \) との交点を \( D \) とします。
このとき、\( △ABC \)∽\( △ADB \) であることを証明しなさい。
【解答】
\( △ABC \) と \( △ADB \) において,
直径 \( AB \) の円周角なので,
\( ∠ACB=90° \) ・・・ ①
直線 \( BD \) は,円 \( O \) の接線なので,
\( ∠ABD=90° \) ・・・ ➁
①➁より,\( ∠ACB=∠ABD=90° \) ・・・ ➂
\( ∠A \) は共通 ・・・ ④
➂④より,2組の角の大きさが等しいので,
\( △ABC \)∽\( △ADB \)
大問10
飛行機に乗るときは,荷物の中に危険物が入っていないか確認するため,荷物をX線検査機に通す検査をすることになっています。
次の図Ⅰは,その荷物検査のようすを真上から見たものです。スーツケースなどの荷物は,ベルトコンベアに乗せられ,矢印 (⇨) の方向に一定の速さで運ばれて,X線検査機を通過します。スーツケースAが,X線検査機に入ってから \( x \; cm \) 進んだとき,スーツケースAとスーツケースBがX線検査機の中に入っている部分の上面の面積の合計を \( y \; cm^2 \) とします。2つのスーツケースの間の距離は \( 40 \; cm \) です。また,X線検査機の長さを \( 1 cm \) ,スーツケースBの上面の面積を \( S \; cm^2 \) とします。なお,どちらのスーツケースも直方体であると考えます。
下の図Ⅱは,\( x \) と \( y \) の関係をグラフに表したものです。
このとき,次の (1) ,(2) の問いに答えなさい。
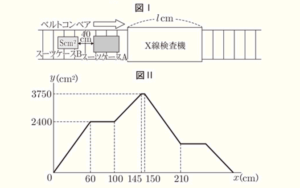
(1) X線検査機の長さ \( l \) と,スーツケースBの上面の面積 \( S \) を求めなさい。
【解答】
\( l=150 \; cm,S=1350 \; cm^2 \)
【解説】
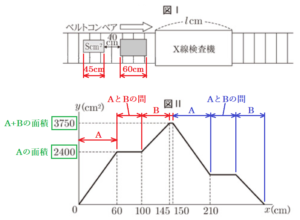
図Ⅱのグラフにおいて,各範囲の直線は次のような状態を示しています。
\( 0~60 \; cm \) ・・・ スーツケースAが検査機の中に入っていく
\( 60~100 \; cm \) ・・・ スーツケースAが検査機に入りきって,スーツケースBが入るまでの間
\( 100~145 \; cm \) ・・・ スーツケースBが検査機の中に入っていく
\( 145~150 \; cm \) ・・・ スーツケースBが検査機に入りきって,スーツケースAが出始めるまでの間
\( 150~210 \; cm \) ・・・ スーツケースAが検査機から出ていく
つまり,スーツケースAは,\( 0 \; cm \) で検査機の中に入り始め,\( 150 \; cm \) で出始めるので,
X線検査機の長さ \( l=150 \; cm \)
また,\( y \) 軸の \( 2400 \; cm^2 \) は,スーツケースAの上面の面積,
\( 3750 \; cm^2 \) は,スーツケースAとBの上面の面積の合計を表しているので,
スーツケースBの上面の面積 \( S=3750-2400=350 \; (cm^2) \)
(2) グラフにおいて,\( x \) の変域が \( 150≦x≦210 \) のとき,\( y \) を \( x \) の式で表しなさい。
【解説】
図Ⅱのグラフから,\( x=210 \) のときにスーツケースAが検査機からすべて出るとわかるので,
\( y \) 座標の値は,\( y=1350 \) になります。
つまり,\( 150≦x≦210 \) のときの直線は,
2点 \( (x,y)=(150,3750),(210,1350) \) を通る直線なので,
傾き \( =\dfrac{1350-3750}{210-150}=-40 \)
この直線の式を \( y=-40x+b \) とすると,
\( 3750=-40 \times 150+b \)
\( b=9750 \)
よって,求める直線の式は,\( y=-40x+9750 \)
大問11
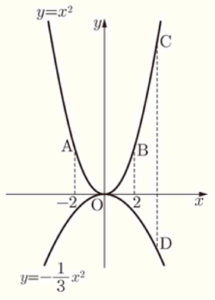
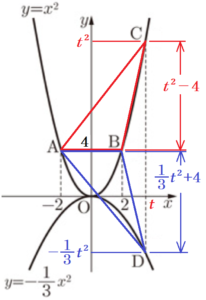
右の図のように,関数 \( y=x^2 \) のグラフ上に3点 \( A,B,C \) があり,関数 \( y=-\dfrac{1}{3}x^2 \) のグラフ上に点 \( D \) があります。\( A,B \) の \( x \) 座標はそれぞれ \( -2,2 \) です。
また,\( C \) と \( D \) の \( x \) 座標は等しく,\( 2 \) より大きくなっています。
このとき,次の (1) ,(2) の問いに答えなさい。
(1) 関数 \( y=x^2 \) について,\( x \) の値が \( 1 \) から \( 2 \) まで増加するときの変化の割合を求めなさい。
【解説】
\( x=1 \) のとき \( y=1 \),\( x=2 \) のとき \( y=4 \) なので,
変化の割合 \( =\dfrac{y の変化量}{x の変化量} \; =\dfrac{4-1}{2-1}=3 \)
(2) \( △ABC \) と \( △ABD \) の面積が等しいとき,点 \( C \) の \( x \) 座標を求めなさい。
【解説】
\( △ABC \) と \( △ABD \) の底辺を線分 \( AB \) と考えると,
\( AB \) は共通なので,高さが等しいとき,面積も等しくなります。
点 \( C \) の \( x \) 座標を \( t \) とすると,
点 \( C \) の \( y \) 座標は,\( y=t^2 \)
点 \( D \) の \( y \) 座標は,\( y=-\dfrac{1}{3}t^2 \)
また,点 \( A,B \) の \( y \) 座標は, \( y=4 \) なので,
\( △ABC \) の高さは,\( t^2-4 \)
\( △ABD \) の高さは,\( \dfrac{1}{3}t^2+4 \)
と表せます。
よって,
\( t^2-4=\dfrac{1}{3}t^2+4 \)
\( 3t^2-12=t^2+12 \)
\( 2t^2=24 \)
\( t^2=12 \)
\( t=2\sqrt{3} \) ( \( t>2 \) より)
大問12
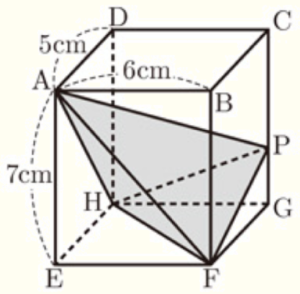
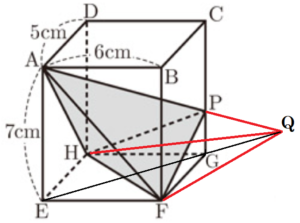
右の図は,\( AB=6cm,AD=5cm,AE=7cm \) の直方体 \( ABCD-EFGH \) です。
このとき,次の (1) ,(2) の問いに答えなさい。
(1) 線分 \( AF \) の長さを求めなさい。
【解答・解説】
\( AF^2=AE^2+EF^2 \)
\( =7^2+6^2 \)
\( =85 \)
\( AF=\sqrt{85} \) ( \( AF>0 \) より)
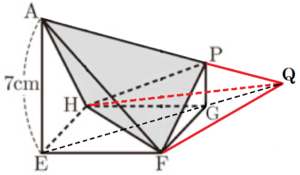
(2) 辺 \( CG \) 上に,\( PG=2cm \) となるような点 \( P \) をとったとき,四面体 \( AHFP \) の体積を求めなさい。
【解説】
線分 \( AP \) と線分 \( EG \) を延長したときの交点を点 \( Q \) とすると,
[四面体\( AHFP \)]\( = \)[三角すい\( A-HFQ \)]\( – \)[三角すい\( P-HFQ \)]
で求められます。
● \( △HFQ \) の面積
線分 \( EG \) と線分 \( FH \) の交点を点 \( J \) とすると,
長方形(平行四辺形)の対角線はそれぞれの中点で交わるので,\( FJ=JH \)
\( △FJQ \) と \( △HJQ \) は底辺の長さが等しく,高さが共通なので,\( △FJQ=△HJQ \)
ここから,\( △HFQ=2△FJQ \) として求めます。
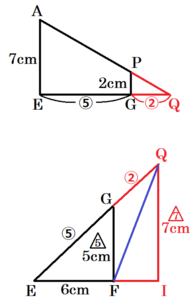
面 \( AEQ \) に注目すると,\( △AEQ \) ∽ \( △PGQ \),\( AE=7cm,PG=2cm \) より,
\( EG:GQ=5:2 \)
点 \( Q \) から線分 \( EF \) の延長線に垂線をひき,交点を \( I \) とします。
面 \( EIQ \) に注目すると,\( △EFG \) ∽ \( △EIQ \),\( EG:GQ=5:2 \) より,
\( FG:IQ=5:7 \)
\( FG=5cm \) より,\( IQ=7cm \)
\( △EFQ=6 \times 7 \times \dfrac{1}{2}=21 \; (cm^2) \)
\( △EFJ \) は四角形 \( EFGH \) の \( \dfrac{1}{4} \) なので,
\( △EFJ=6 \times 5 \times \dfrac{1}{4}=\dfrac{15}{2} \; (cm^2) \)
よって,
\( △FJQ=△EFQ-△EFJ=21-\dfrac{15}{2}=\dfrac{27}{2} \; (cm^2) \)
\( △HFQ=2△FJQ=2 \times \dfrac{27}{2}=27 \; (cm^2) \)
[四面体\( AHFP \)]\( = \)[三角すい\( A-HFQ \)]\( – \)[三角すい\( P-HFQ \)]
\( =27 \times 7 \times \dfrac{1}{3}-27 \times 2 \times \dfrac{1}{3} \)
\( =27 \times (7-2) \times \dfrac{1}{3} \)
\( =45 \; (cm^3) \)