大問1
(1) 次のア~オを計算しなさい。
ア \( 4-10 \)
イ \( (-2)^2 \times 3+(-15) \div (-5) \)
【解説】
\( =4 \times 3+3 \)
\( =12+3 \)
\( =15 \)
ウ \( \begin{array}{rr}
&6x^2-x-5 \\
-) &2x^2+x-6 \\
\hline
\end{array} \)
【解答・解説】
\( \begin{array}{rr}
&6x^2-x-5 \\
-) &2x^2+x-6 \\
\hline
&4x^2-2x+1
\end{array} \)
エ \( (6x^2y+4xy^2) \div 2xy \)
【解説】
\( =\dfrac{6x^2y}{2xy}+\dfrac{4xy^2}{2xy} \)
\( =3x+2y \)
オ \( \sqrt{\dfrac{3}{2}}-\dfrac{ \sqrt{54}}{2} \)
【解説】
\( =\dfrac{\sqrt{3}}{\sqrt{2}}-\dfrac{3\sqrt{6}}{2} \)
\( =\dfrac{\sqrt{3} \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}-\dfrac{3\sqrt{6}}{2} \)
\( =\dfrac{\sqrt{6}}{2}-\dfrac{3\sqrt{6}}{2} \)
\( =\dfrac{-2\sqrt{6}}{2} \)
\( =-\sqrt{6} \)
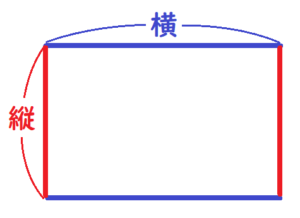
(2) 縦が \( x \; cm \),横が \( y \; cm \) の長方形がある。このとき,\( 2(x+y) \) は長方形のどんな数量を表しているか,書きなさい。
【解説】
\( 2(x+y)=2 \times (x+y) \) で,\( x+y \) は,「縦+横」を表しています。
ここから,\( 2(x+y)=2 \times (x+y) \) は,「縦+横」が2つ,
つまり,縦と横が2つずつなので,表しているのは長方形の周の長さになります。
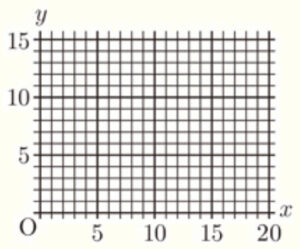
(3) 右の表は,あるクラスの生徒20人のハンドボール投げの記録を度数分布表に整理したものである。記録が \( 20 \; m \) 以上 \( 24 \; m \) 未満の階級の相対度数を求めなさい。また,\( 28 \; m \) 未満の累積相対度数を求めなさい。
【解答】
\( 20 \; m \) 以上 \( 24 \; m \) 未満の階級の相対度数 ・・・ \( 0.30 \)
\( 28 \; m \) 未満の累積相対度数 ・・・ \( 0.55 \)
【解説】
【相対度数】
ある階級の相対度数は,「その階級の度数 \( \div \) データの総数」で求めることができます。
\( 20 \; m \) 以上 \( 24 \; m \) 未満の階級の度数は \( 6 \),データの総数は \( 20 \) なので,
\( 6 \div 20=0.30 \)
【累積相対度数】
ある階級の相対度数は,「求める範囲の累積度数 \( \div \) データの総数」で求めることができます。
\( 28 \; m \) 未満の累積度数は \( 4+6+1=11 \),データの総数は \( 20 \) なので,
\( 11 \div 20=0.55 \)
(4) 次の式を因数分解しなさい。
\( 3x^2-6x-45 \)
【解説】
\( =3(x^2-2x-15) \)
\( =3(x+3)(x-5) \)
(5) 関数 \( y=ax+b \) について,\( x \) の値が \( 2 \) 増加すると \( y \) の値が \( 4 \) 増加し,\( x=1 \) のとき \( y=-3 \) である。このとき,\( a,b \) の値をそれぞれ求めなさい。
【解説】
\( x \) の値が \( 2 \) 増加すると \( y \) の値が \( 4 \) 増加することから,
傾き \( a=\dfrac{4}{2}=2 \)
\( y=2x+b \) に \( x=1,y=-3 \) を代入すると,
\( -3=2 \times 1+b \)
\( b=-5 \)
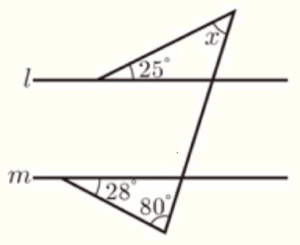
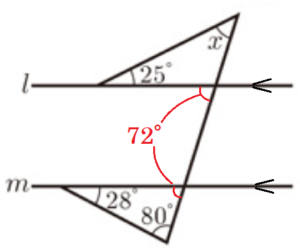
(6) 右の図で,\( l//m \) のとき,\( ∠x \) の大きさを求めなさい。
【解説】
下側の三角形において,残りの1つの角の大きさは
\( 180°-(28°+80°)=72° \)
\( l//m \) より,同位角は等しいので,上側の三角形の外角も \( 72° \)
よって,
\( x+25°=72° \)
\( x=47° \)
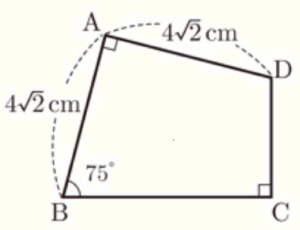
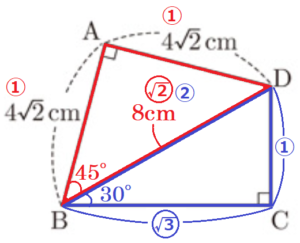
(7) 右の図で,辺 \( BC \) の長さを求めなさい。
【解答】
\( 4\sqrt{3} \; cm \)
【解説】
\( AB=AD=4\sqrt{2} \; cm,∠BAD=90° \) より,
\( △ABD \) は直角二等辺三角形なので,
\( BD= \sqrt{2}AB=8 \; (cm) \)
\( ∠ABD=45° \)より,\( ∠CBD=75°-45°=30° \)
\( ∠CBD=30°,∠BCD=90° \) より,
\( △BCD \) は \( 30°,60°,90° \) の直角三角形なので,
\( BD:BC=2: \sqrt{3} \)
よって,
\( BD:BC=2: \sqrt{3} \)
\( 8:BC=2:\sqrt{3} \)
\( 2BC=8\sqrt{3} \)
\( BC=4\sqrt{3} \; (cm) \)
(8) データの分布を表す値や箱ひげ図について述べた文として適切でないものを,次のア~エの中から1つ選び,その記号を書きなさい。
ア 第2四分位数と中央値は,かならず等しい。
イ データの中に極端にかけ離れた値があるとき,四分位範囲はその影響を受けにくい。
ウ 箱ひげ図を横向きにかいたとき,箱の横の長さは範囲 (レンジ)を表している。
エ 箱ひげ図の箱で示された区間には,全体の約50%のデータがふくまれる。
【解説】
ア 第2四分位数と中央値は,呼び方の違いだけで同じもの(値)を表しています。
イ データの中に極端にかけ離れた値があるとき,ひげの長さが長くなるだけなので,
四分位範囲にはほぼ影響はありません。
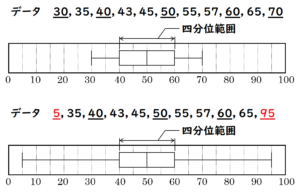
ウ 上の図にもある通り,箱の横の長さは四分位範囲を表しています。
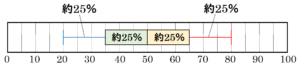
エ 第二四分位数は,すべてのデータを上下半分ずつに分ける値になります。
また,第一四分位数は,下半分のデータをさらに半分ずつにわけます。
同様に,第三四分位数は,上半分のデータをさらに半分ずつにわけます。
つまり,左右(上下)のひげの部分,箱の部分を第二四分位数を境に左右(上下)に分けた部分には
それぞれ約25%のデータが含まれることになります。
ここから,箱で示された区間には,全体の約50%のデータがふくまれることになります。
大問2
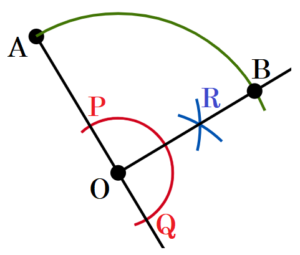
(1) 下の図の点 \( A \) を点 \( O \) を中心として,時計回りに \( 90° \) 回転移動させた点 \( B \) を作図によって求めなさい。ただし,作図に使った線は消さないこと。
【解答・解説】
問題の条件から,\( ∠AOB=90° \) なので,
点 \( O \) を通り,直線 \( OA \) と垂直な直線を作図し,
この直線と線分 \( OA \) を半径とする円弧との交点が
点 \( B \) になります。
手順1 直線 \( OA \) を描く。
手順2 点 \( O \) を中心に円弧を描く。
(直線 \( OA \) との交点を点 \( P,Q \) とします。)
手順3 2点 \( P,Q \) を中心に円弧を描く。
(交点を点 \( R \) とします。)
手順4 2点 \( O,R \) を通る直線を描く。
手順4の直線と線分 \( OA \) を半径とする円弧との交点が
点 \( B \) になります。
(2) 下の [問題]とそれについて考えているレンさんとメイさんの会話を読んで,次のア,イに答えなさい。
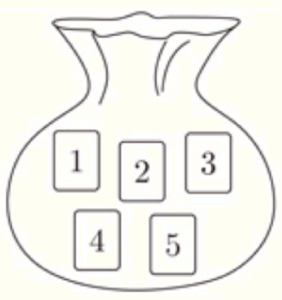
[問題] 右の図のように,1から5までの数字が書かれた5枚のカードが袋の中に入っている。このカードをよくまぜてから1枚ずつ続けて3回取り出し,取り出した順に左から並べて3けたの整数をつくる。
このとき,3けたの整数が350以上になる確率を求めなさい。
レン:例えば,1回目に1,2回目に3,3回目に4のカードを取り出したら,3けたの整数は134で,これは [問題] の条件を満たさないよね。
メイ:3けたの整数は全部で あ 通りできるよ。 X の位に着目して考えてみてはどうかな。
レン:そうか。 X の位が3のときは,条件を満たす整数がいくつかできるね。
メイ:あとは,他の2つの位がどのカードになるかを考えると, X の位が3のとき,条件を満たす整数は い 通りできるよ。
レン:[問題] を解くためには, X の位が3のときだけではなく, う , え のときも考えなければいけないね。
メイ:そうだよ。そうやって少しずつ条件を整理して考えると,確率を求めることができるんだ。
ア あ ~ え にあてはまる数をそれぞれ書きなさい。また, X に共通してあてはまる位を書きなさい。
【解答】
あ ・・・ \( 60 \), い ・・・ \( 3 \), う ・・・ \( 4 \), え ・・・ \( 5 \)
X ・・・ 百
【解説】
百の位が \( 1 \) のとき,できる3けたの数字は
\( 123,124,125,132,134,135,142,143,145,152,153,154 \) の12通りです。
同様に百の位が \( 2 \) のとき,\( 3 \) のとき,・・・,\( 5 \) のとき も12通りずつなので,
すべての場合の数は60通りになります。
3けたの整数が350以上になるということは,
百の位の数字(1回目に取り出す数字)は \( 3,4,5 \) のどれかでなければなりません。
イ [問題] を解きなさい。
【解説】
【1回目に取り出した数字が \( 3 \) であった場合】
2回目に取り出す数字は \( 5 \) でなければなりません。
なので,このとき,できる3けたの整数は \( 351,352,354 \) の3通りです。
【1回目に取り出した数字が \( 4 \) であった場合】
2回目,3回目はどのような組み合わせで取り出しても3けたの整数は350以上になります。
なので,このとき,できる3けたの整数は ア で考えた通り12通りです。
【1回目に取り出した数字が \( 5 \) であった場合】
2回目,3回目はどのような組み合わせで取り出しても3けたの整数は350以上になります。
なので,このとき,できる3けたの整数は ア で考えた通り12通りです。
以上より,条件を満たす整数は27通りになるので,
求める確率は \( \dfrac{27}{60}=\dfrac{9}{20} \)
大問3
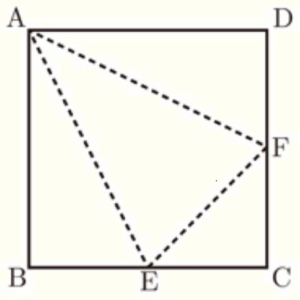
(1) 1辺の長さが \( 8 \; cm \) の正方形の紙 \( ABCD \) がある。右の図は,辺 \( BC,CD \) の中点をそれぞれ \( E,F \) とし,線分 \( AE,EF,FA \) で折ってできる三角錐の展開図である。次のア,イに答えなさい。
ア 線分 \( AE \) の長さを求めなさい。
【解答】
\( 4\sqrt{5} \; cm \)
【解説】
点 \( E \) は辺 \( BC \) の中点なので,\( BE=\dfrac{1}{2}BC=4 \; (cm) \)
\( △ABE \) において,三平方の定理より,
\( AE^2=8^2+4^2=80 \)
\( AE=4\sqrt{5} \; (cm) \)(\( AE>0 \)より )
イ 折ってできる三角錐について,次の (ア) ,(イ)に答えなさい。
(ア) 体積を求めなさい。
【解答】
\( \dfrac{64}{3} \; cm^3 \)
【解説】
できる三角すいは下の図のようになります。
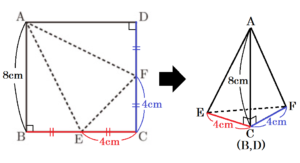
三角すいを組み立てたとき,点 \( B,D \) は点 \( C \) と重なるので,求める体積は,
\( \left(4 \times 4 \times \dfrac{1}{2} \right) \times 8 \times \dfrac{1}{3}=\dfrac{64}{3} \; (cm^3) \)
(イ) \( △AEF \) を底面としたときの高さを求めなさい。
【解答】
\( \dfrac{8}{3} \; cm \)
【解説】
\( △AEF= \)正方形 \( ABCD-△ABE-△ADF-△CEF \) と考えると,
\( △ABE=△ADF=4 \times 8 \times \dfrac{1}{2}=16 \; (cm^2) \)
\( △CEF=4 \times 4 \times \dfrac{1}{2}=8 \; (cm^2) \)
なので,\( △AEF=64-16 \times 2-8=24 \; (cm^2) \)
(ア)より,三角すいの体積は \( \dfrac{64}{3} \; cm^3 \) なので,
求める高さを \( h \; cm \) とすると,
\( 24 \times h \times \dfrac{1}{3}=\dfrac{64}{3} \)
\( 24h=64 \)
\( h=\dfrac{8}{3} \; (cm) \)
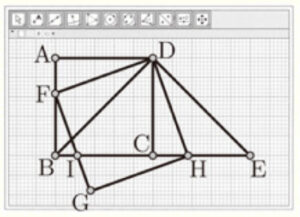
(2) 下の図のように,作図ソフトで正方形 \( ABCD \) と \( DB=DE \) の直角二等辺三角形 \( DBE \) をかき,辺 \( AB \) 上に動く点 \( F \) をとる。また,線分 \( DF \) を1辺とする正方形 \( DFGH \) をかくと,点 \( H \) は辺 \( CE \) 上を動く点であることがわかった。辺 \( BC \) と辺 \( FG \) の交点を \( I \) とするとき,次のア,イに答えなさい。
ア \( △DFB \) と \( △DHE \) が合同になることを次のように証明した。
あ , い には式, う には適切な内容をそれぞれ書きなさい。
[証明]
\( △DFB \) と \( △DHE \) において
\( △DBE \) は二等辺三角形だから
\( DB=DE \) ・・・ ➀
四角形 \( DFGH \) は正方形だから
あ ・・・ ➁
また、2つの直角三角形 \( DAF \) と \( DCH \) において
\( ∠DAF=∠DCH=90°,DF=DH,DA=DC \) であるから \( △DAF≡△DCH \)
したがって,\( ∠ADF=∠CDH \) であり
\( ∠BDF=45°-∠ADF,∠EDH=45°-∠CDH \) であるから
い ・・・ ➂
➀,➁,➂から
う がそれぞれ等しいので
\( △DFB≡△DHE \)
【解答】
あ ・・・ \( DF=DH \), い ・・・ \( ∠BDF=∠EDH \), う ・・・ 2組の辺とその間の角
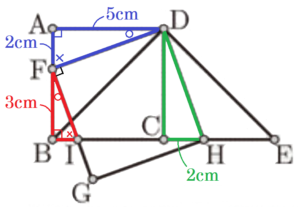
イ \( AB=5 \; cm,CH=2 \; cm \) のとき,\( △FBI \) の面積を求めなさい。
【解答】
\( \dfrac{9}{5} \; cm^2 \)
【解説】
\( △DAF \) において,
\( ∠ADF=180°-∠FAD-∠AFD \)
\( =90°-∠AFD \) ・・・ ➀
点 \( F \) は線分 \( AB \) 上の点なので,
\( ∠IFB=180°-∠DFI-∠AFD \)
\( =90°-∠AFD \) ・・・ ➁
➀➁より,\( ∠ADF=∠IFB \) ・・・ ➂
正方形の内角はすべて \( 90° \) なので,
\( ∠DAF=∠FBI=90° \) ・・・ ➃
➂➃より,2組の角がそれぞれ等しいので,
\( △DAF \) ∽ \( △FBI \)
ア より \( △DAF≡△DCH \) なので,\( AF=CH=2 \; cm \)
\( AB=5 \; cm \) なので,\( FB=AB-AF=3 \; cm \)
\( △DAF \) ∽ \( △FBI \) で,
相似な三角形の対応する辺の比は等しいので,
\( DA:FB=AF:BI \)
\( 5:3=2:BI \)
\( 5BI=6 \)
\( BI=\dfrac{6}{5} \; (cm) \)
よって,
\( △FBI=3 \times \dfrac{6}{5} \times \dfrac{1}{2} \)
\( =\dfrac{9}{5} \; (cm^2) \)
大問4
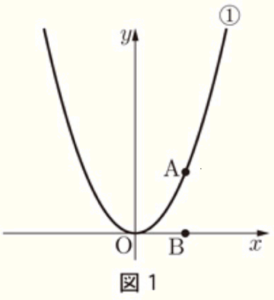
図1で,➀ は関数 \( y=ax^2 \: (a>0) \) のグラフである。点 \( A \) は ➀ 上にあり,\( x \) 座標が \( 2 \) である。また,点 \( B \) は \( x \) 軸上にあり,\( x \) 座標は点 \( A \) の \( x \) 座標と同じである。次の(1) ,(2)に答えなさい。
ただし,座標軸の単位の長さを \( 1 \; cm \) とする。
(1) 次のア,イに答えなさい。
ア \( a=\dfrac{1}{2} \) のとき,点 \( A \) の \( y \) 座標を求めなさい。
【解説】
点 \( A \) の \( x \) 座標は \( 2 \) なので,
\( y=\dfrac{1}{2} \times 2^2=2 \)
イ 2点 \( A,B \) 間の距離が \( 6 \; cm \) のとき,\( a \) の値を求めなさい。
【解答】
\( a=\dfrac{3}{2} \)
【解説】
点 \( B \) は \( x \) 軸上にあるので,\( y \) 座標の値は \( 0 \) です。
つまり,2点 \( A,B \) 間の距離が \( 6 \; cm \) のとき,
点 \( A \) の \( y \) 座標の値は \( 6 \) になります。
ここから,点 \( A \) の座標は \( (2,6) \) なので,
\( y=ax^2 \) に \( x=2,y=6 \) を代入すると,
\( 6=a \times 2^2 \)
\( 4a=6 \)
\( a=\dfrac{3}{2} \)
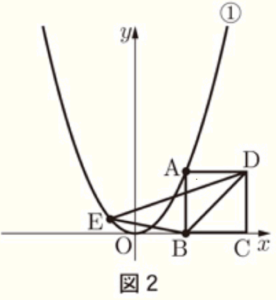
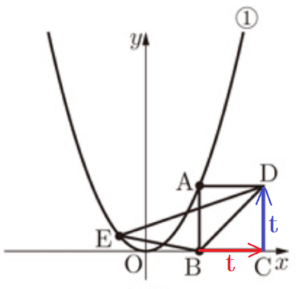
(2) 図2は,図1に正方形 \( ABCD \) と \( △BDE \) をかき加えたもので,点 \( E \) は ➀ 上にあり,\( x \) 座標は \( -1 \) である。このとき,次のア,イに答えなさい。ただし,点 \( C \) の \( x \) 座標は点 \( B \) の \( x \) 座標より大きいものとする。
ア 2点 \( B,D \) を通る直線の式を求めなさい。
【解説】
正方形はすべての辺の長さが等しいので,\( BC=t \) とするとき,
\( CD=t \) でもあります。
2点 \( B,D \) 間において,\( x \) 座標の値が \( t \) 増える間に
\( y \) 座標の値も \( t \) 増えるので,直線 \( BD \) の傾きは,
傾き \( =\dfrac{yの増加量}{xの増加量} \) \( =\dfrac{t}{t}=1 \)
直線 \( BD \) の式を \( y=x+b \) とすると,\( B(2,0) \) を通るので,
\( 0=2+b \)
\( b=-2 \)
よって,直線 \( BD \) の式は,\( y=x-2 \)
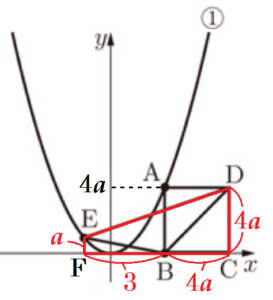
イ \( △BDE \) の面積が \( 80 \; cm^2 \) であるとき,\( a \) の値を求めなさい。
【解説】
点 \( E \) から \( x \) 軸に垂線をひいた交点を \( F \) とし,
\( △BDE= \) 台形 \( EFCD-△BEF-△BCD \)
として求めます。
点 \( A \) の \( x \) 座標は \( 2 \) なので,\( y \) 座標は \( 4a \) になります。
正方形はすべての辺の長さが等しいので,
\( AB=BC=CD=4a \) になります。
また,点 \( E \) の \( x \) 座標は \( -1 \) なので,\( y \) 座標は \( a \) になります。
このとき,
台形 \( EFCD=(a+4a) \times (3+4a) \times \dfrac{1}{2} \)
\( =\dfrac{5}{2}a(3+4a) \)
\( △BEF=3 \times a \times \dfrac{1}{2} \)
\( =\dfrac{3}{2}a \)
\( △BCD=4a \times 4a \times \dfrac{1}{2} \)
\( =8a^2 \)
よって,
\( △BDE= \) 台形 \( EFCD-△BEF-△BCD \)
\( 80=\dfrac{5}{2}a(3+4a)-\dfrac{3}{2}a-8a^2 \)
\( 80=2a^2+6a \)
\( a^2+3a-40=0 \)
\( (a-5)(a+8)=0 \)
\( a=5,-8 \)
\( a>0 \) より,あてはまるのは,\( a=5 \)
大問5
マユさんとリクさんは数学の授業で,下のように,ホワイトボードに書かれた【問題】を解いた。
次の(1) ,(2) に答えなさい。
【問題】
1個120円のりんごと1個150円のなしがある。1つの箱にりんごとなしを詰め合わせて,箱代40円をふくめて6700円になるとき,詰め合わせたりんごとなしの個数をそれぞれ求めなさい。
ただし,次の〔条件〕を満たすこと。
〔条件〕 りんごとなしを合わせて50個詰め合わせる。
〔マユさん〕
りんごを \( a \) 個とすると、
なしは あ 個とすることができる。
\( a \) についての方程式をつくると,
\( 120a+150 \) あ \( +40=6700 \) となる。
これを解くと,\( a=28 \) となるので,
りんご \( 28 \) 個,なし \( 22 \) 個
〔リクさん〕
りんごを \( a \) 個,なしを \( b \) 個とする。
\( a,b \) についての連立方程式をつくると、
い
これを解くと,\( a=28 \),\( b=22 \)となるので,
りんご \( 28 \) 個,なし \( 22 \) 個
(1) あ , い にあてはまる式をそれぞれ書きなさい。
【解答】
あ ・・・ \( 50-a \)
い ・・・ \( \left\{ \begin{array}{}120a+150b+40=6700 \\
a+b=50 \\
\end{array} \right. \)
(2) 【問題】を解いた後,先生からプリントが配られた。下は,マユさんが取り組んだプリントの一部である。次の ア,イ に答えなさい。
●【問題】の〔条件〕を次の〔条件A〕と〔条件B〕に変えて,その2つを満たすりんごとなしの個数をそれぞれ求めましょう!
〔条件A〕 りんごとなしはどちらも \( 18 \) 個以上詰め合わせる。
〔条件B〕 りんごとなしを合わせて \( 50 \) 個より多く詰め合わせる。
〔解答〕
〔条件A〕を満たすために,りんごとなしの個数をそれぞれ \( (x+18) \) 個,\( (y+18) \) 個 とする。
(\( x,y \) は \( 0 \) 以上の整数)
\( x,y \) についての二元一次方程式をつくると、
う \( =6700 \) となる。
え
これを整理すると, \( 4x+5y=60 \) となる。
この式の解を座標とする点は,すべて1つの直線上にあるから,
〔条件A〕を満たす \( x,y \) の値は,次の4組である。
\( (x, y)=\fbox{ ( , ) ,( , ) ,( , ) ,( , ) } \)
お
さらに,〔条件B〕を満たすのは、
\( (x, y)=\fbox{ ( , ) } \) だけだから、
りんご \( ▭ \) 個,なし \( ▭ \) 個となる。
● 今日の授業を通して,気づいたことを書きましょう!
ア う にあてはまる式を書きなさい。
【解答】
\( 120(x+18)+150(y+18)+40 \)
イ え , お の \( ▭ \) について,あてはまる座標や数をそれぞれ求めなさい。
【解答】
え ・・・ \( (0,12),(5,8),(10,4),(15,0) \)
お ・・・ \( (15,0) \)
りんご \( 33 \) 個,
なし \( 18 \) 個
【解説】
え
\( 4x+5y=60 \) を \( y \) について解くと,\( y=-\dfrac{4}{5}x+12 \)
この直線をグラフに表すと,
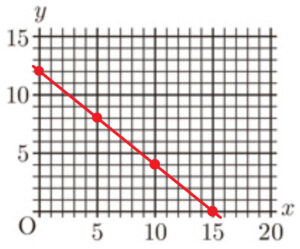
この直線上の点で,\( x,y \) がともに \( 0 \) 以上の整数になるのは,
\( (x, y)=(0,12),(5,8),(10,4),(15,0) \)
お
りんごとなしの個数の合計は \( (x+18)+(y+18)=x+y+36 \) 個と表すことができ,
50個より多くなるのだから,〔条件B〕を満たすとき,
\( x+y+36>50 \) つまり,\( x+y>14 \) となります。
\( (x, y)=(0,12),(5,8),(10,4),(15,0) \) のうち,
\( x+y>14 \) を満たすのは,\( (x, y)=(15,0) \) のときだけなので,
りんごの個数は,\( 15+18=33 \) 個,
なしの個数は,\( 0+18=18 \) 個
となります。