関数のグラフと図形を組み合わせた問題は,高校入試でよく出ます。
グラフと図形の面積の問題の中でもよく出る,
\(x\)軸または\(y\)軸に平行な辺を持たない三角形の面積
をより簡単に求める方法を紹介します。
ここでは,\(y=\dfrac{1}{5}x+5\) と \(y=2x-13\) と \(y=-x+5\) の
3本の直線で囲まれた三角形の面積を求めてみます。
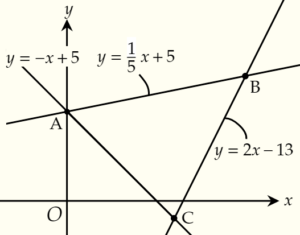
鉄則:\(x\)軸または\(y\)軸に平行な直線を利用する
普通に求めると面倒すぎる・・・
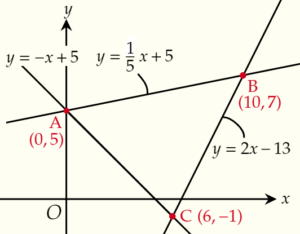
1.頂点A,B,Cの座標を求める
\(y=-x+5\) より,点Aの座標は,A\((0,5)\) です。
点Bは \(y=\dfrac{1}{5}x+5\) と \(y=2x-13\) 上の点なので,
この2式を連立方程式として解くと,\(x=10,y=7\)となります。
よって,B\((10,7)\) です。
点Cは \(y=-x+5\) と \(y=2x-13\) 上の点なので,
この2式を連立方程式として解くと,\(x=6,y=-1\)となります。
よって,C\((6,-1)\) です。
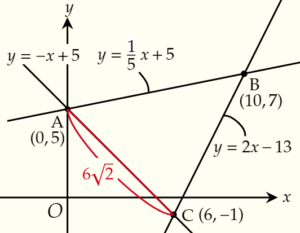
2.底辺ACの長さを求める
ここでは,辺ACを底辺とすると,
AC=\(\sqrt{(6-0)^2+\{5-(-1)\}^2}\)
=\(\sqrt{72}\)
=\(6\sqrt{2}\)
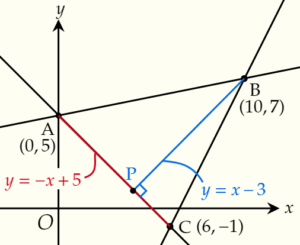
3.直線BPの式を求める
点Bから辺ACに垂線をひき,交点をPとします。
このとき,AC⊥BPなので,
直線ACの傾き × 直線BPの傾き = \(-1\)
\(-1\) × 直線BPの傾き = \(-1\)
直線BPの傾き = \(-1\)
ここで,直線BPの式を \(y=x+b\) とすると,
B\((10,7)\) を通るので,
\(y=x+b\)
\(7=10+b\)
\(b=-3\)
よって,直線BPの式は \(y=x-3\) となります。
4.点Pの座標を求める
点Bは \(y=-x+5\) と \(y=x-3\) 上の点なので,
この2式を連立方程式として解くと,\(x=4,y=1\)となります。
よって,P\((4,1)\) です。
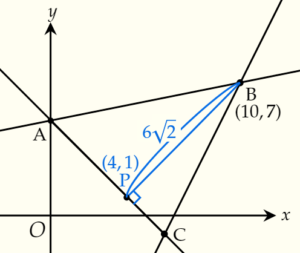
5.高さBPを求める
BP=\(\sqrt{(10-4)^2+(7-1)^2}\)
=\(\sqrt{72}\)
=\(6\sqrt{2}\)
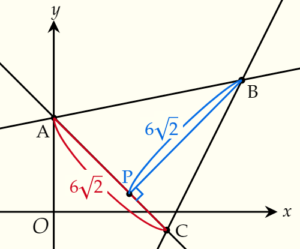
6.△ABCの面積を求める
△ABC=AC×BP×\(\dfrac{1}{2}\)
=\(6\sqrt{2} \times 6\sqrt{2} \times \dfrac{1}{2} \)
=\(36\; (cm^2)\)
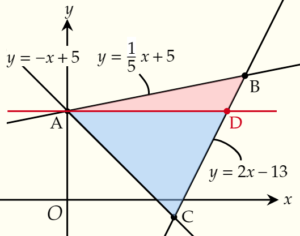
方法1:\(x\)軸に平行な直線で2つの三角形に分けて求める
右の図のように,△ABCを\(x\)軸に平行な直線で2つの三角形に
分けることで,より簡単に面積を求めることができます。
△ABC=△ABD+△ACD
1.頂点A,B,Cの座標を求める
\(y=-x+5\) より,点Aの座標は,A\((0,5)\) です。
点Bは \(y=\dfrac{1}{5}x+5\) と \(y=2x-13\) 上の点なので,
この2式を連立方程式として解くと,\(x=10,y=7\)となります。
よって,B\((10,7)\) です。
点Cは \(y=-x+5\) と \(y=2x-13\) 上の点なので,
この2式を連立方程式として解くと,\(x=6,y=-1\)となります。
よって,C\((6,-1)\) です。

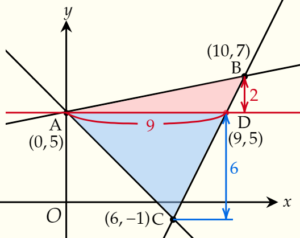
2.頂点Aから\(x\)軸に平行な直線をひき,点Dの座標を求める
点Aを通り,\(x\)軸に平行な直線をひき,辺BCとの交点をDとすると,点Dは \(y=5\) と \(y=2x-13\) 上の点なので,
この2式を連立方程式として解くと,\(x=9\)となります。
よって,D\((9,5)\) です。
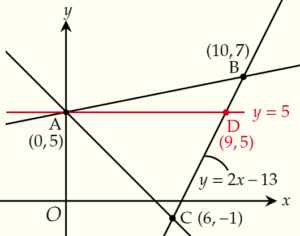
3.△ABDと△ACDの面積を求める
ADを底辺として考えると,
AD=Dの\(x\)座標-Aの\(x\)座標
=\(9-0\)
=\(9\)
△ABDの高さ=Bの\(y\)座標-Dの\(y\)座標
=\(7-5\)
=\(2\)
△ACDの高さ=Dの\(y\)座標-Cの\(y\)座標
=\(5-(-1)\)
=\(6\)
と表すことができるので,
△ABD=\(9 \times 2 \times \dfrac{1}{2}\)
=\(9\; (cm^2)\)
△ACD=\(9 \times 6 \times \dfrac{1}{2}\)
=\(27\; (cm^2)\)
4.△ABCの面積を求める
△ABCは,△ABDと△ACDの和となっているので,
△ABC=△ABD+△ACD
=\(9+27\)
=\(36\; (cm^2)\)
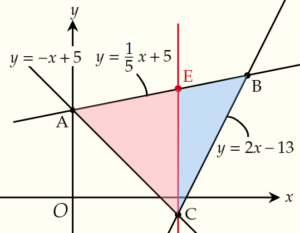
方法2:\(y\)軸に平行な直線で2つの三角形に分けて求める
同様に,△ABCを\(y\)軸に平行な直線で2つの三角形に
分ける方法もあります。
△ABC=△ACE+△BCE
1.頂点A,B,Cの座標を求める
3点の座標は,A\((0,5)\) ,B\((10,7)\) ,C\((6,-1)\) です。
求め方は\(x\)軸に平行な直線の場合と同じなので省略します。

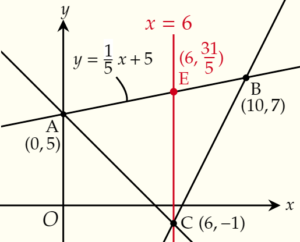
2.頂点Cから\(y\)軸に平行な直線をひき,点Eの座標を求める
点Cを通り,\(y\)軸に平行な直線をひき,辺ABとの交点をEとすると,点Eは \(x=6\) と \(y=\dfrac{1}{5}x+5\) 上の点なので,
この2式を連立方程式として解くと,\(y=\dfrac{31}{5}\)となります。
よって,E\((6,\dfrac{31}{5})\) です。
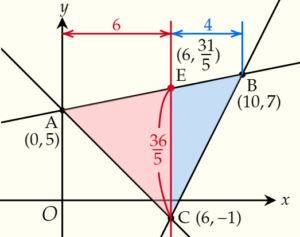
3.△ACEと△ABEの面積を求める
CEを底辺として考えると,
CE=Eの\(y\)座標-Cの\(y\)座標
=\(\dfrac{31}{5}-(-1)\)
=\(\dfrac{36}{5}\)
△ACEの高さ=Eの\(x\)座標-Aの\(x\)座標
=\(6-0\)
=\(6\)
△BCEの高さ=Bの\(x\)座標-Eの\(x\)座標
=\(10-6\)
=\(4\)
と表すことができるので,
△ACE=\(\dfrac{36}{5} \times 6 \times \dfrac{1}{2}\)
=\(\dfrac{108}{5}\; (cm^2)\)
△BCE=\(\dfrac{36}{5} \times 4 \times \dfrac{1}{2}\)
=\(\dfrac{72}{5}\; (cm^2)\)
4.△ABCの面積を求める
△ABCは,△ACEと△BCEの和となっているので,
△ABC=△ACE+△BCE
=\(\dfrac{108}{5}+\dfrac{72}{5}\)
=\(36\; (cm^2)\)
問題によってうまく使い分けよう
\(x\)軸に平行な直線を使うか\(y\)軸に平行な直線に平行な直線を使うかは問題によります。
今回の例では,\(x\)軸に平行な直線を使う方が底辺や高さが自然数になるので,計算しやすくなります。
試験時間には限りがあり,より難しい問題に時間をかけたいので,解き方を工夫することも覚えていきましょう。

-120x68.jpg)
