大問1
(1) \( 8+12 \div (-4) \) を計算しなさい。
(2) \( 12ab \div 6a^2 \times 2b \) を計算しなさい。
【解答】
\( \dfrac{4b^2}{a} \)
【解説】
\( =\dfrac{12ab \times 2b}{6a^2} \)
\( =\dfrac{4b^2}{a} \)
(3) 次の数の大小を,不等号を使って表しなさい。
\( 4,\sqrt{10} \)
【解説】
\( 4 \) を \( \sqrt{} \) を使って表すと,\( \sqrt{16} \) になります。
よって,\( \sqrt{16}>\sqrt{10} \) なので,\( 4>\sqrt{10} \) となります。
(4) \( x=\dfrac{1}{2},y=-3 \) のとき,\( 2(x-5y)+5(2x+3y) \) の値を求めなさい。
【解説】
\( 2(x-5y)+5(2x+3y)=12x+5y \) なので,
\( x=\dfrac{1}{2},y=-3 \) を代入すると,
\( 12 \times \dfrac{1}{2}+5 \times (-3) \)
\( =6-15 \)
\( =-9 \)
(5) \( \dfrac{\sqrt{2}}{2}-\dfrac{1}{3\sqrt{2}} \) を計算しなさい。
【解答】
\( \dfrac{\sqrt{2}}{3} \)
【解説】
\( =\dfrac{\sqrt{2}}{2}-\dfrac{1 \times \sqrt{2}}{3\sqrt{2} \times \sqrt{2}} \)
\( =\dfrac{3\sqrt{2}}{6}-\dfrac{\sqrt{2}}{6} \)
\( =\dfrac{\sqrt{2}}{3} \)
(6) 方程式 \( \dfrac{5x-2}{4}=7 \) を解きなさい。
【解説】
\( 5x-2=28 \)
\( 5x=30 \)
\( x=6 \)
(7) 連立方程式 \( \left\{ \begin{array}{}
2x+y=5 \\
x-4y=7 \\ \end{array} \right. \) を解きなさい。
【解説】
\( 2x+y=5 \) ・・・ ➀
\( x-4y=7 \) ・・・ ➁
➁\( \times 2\)すると,
\( 2x-8y=14 \) ・・・ ➁’
➀\( – \)➁’すると,
\( 9y=-9 \)
\( y=-1 \)
➁に代入すると,
\( x-4 \times (-1)=7 \)
\( x+4=7 \)
\( x=3 \)
(8) 方程式 \( x^2+5x+2=0 \) を解きなさい。
【解答】
\( x=\dfrac{-5±\sqrt{17}}{2} \)
【解説】
\( ax^2+bx+c=0 \) と考えると,\( a=1,b=5,c=2 \) なので,
解の公式から,
\( x=\dfrac{-5±\sqrt{5^2-4 \times 1 \times 2}}{2 \times 1} \)
\( =\dfrac{-5±\sqrt{17}}{2} \)
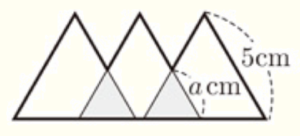
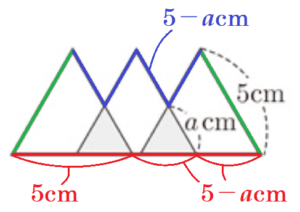
(9) 右の図のように,1辺の長さが \( 5 \; cm \) の正三角形の紙を,その一部が重なるように,横一列に3枚並べて図形をつくる。このとき,重なる部分はすべて1辺の長さが \( a \; cm \) の正三角形となるようにする。図の太線は,図形の周囲を表している。太線で表した図形の周囲の長さを, \( a \) を用いた式で表しなさい。
【解説】
この図形の周囲の長さを右の図のように分けて考えると,
緑 ・・・ \( 5 \; cm \times 2 \)本
青 ・・・ \( (5-a) \; cm \times 4 \)本
赤 ・・・ \( 5 \; cm \times 1 \)本 \( +(5-a) \; cm \times 2 \)本
となっています。
よって,周の長さは,
\( 5 \times 2+(5-a)\times 4+{5 \times 1+(5-a)\times 2} \)
\( =10+(20-4a)+{5+(10-2a)} \)
\( =45-6a \; (cm) \)
(10) \( n \) は \( 100 \) より小さい素数である。 \( \dfrac{231}{n+2} \) が整数となる \( n \) の値をすべて求めなさい。
【解説】
\( \dfrac{231}{n+2} \) が整数となるのは,\( n+2 \) が \( 231 \) の約数になるときです。
\( 231 \) を素因数分解すると \( 3 \times 7 \times 11 \) なので,
約数は,\( 3 \) と \( 7 \) と \( 11 \) のすべての組み合わせになります。
よって,\( 231 \) のすべての約数は,\( 1,3,7,11,21,33,77,231 \) です。
\( n+2=1 \) のとき,\( n=-1 \) → 素数ではない
\( n+2=3 \) のとき,\( n=1 \) → 素数ではない
\( n+2=7 \) のとき,\( n=5 \) → ○
\( n+2=11 \) のとき,\( n=9 \) → 素数ではない
\( n+2=21 \) のとき,\( n=19 \) → ○
\( n+2=33 \) のとき,\( n=31 \) → ○
\( n+2=77 \) のとき,\( n=75 \) → 素数ではない
\( n+2=231 \) のとき,\( n=229 \) → \( 100 \) より大きい
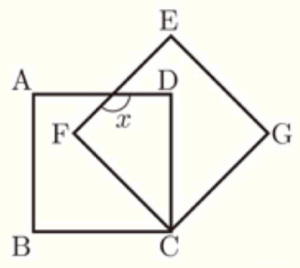
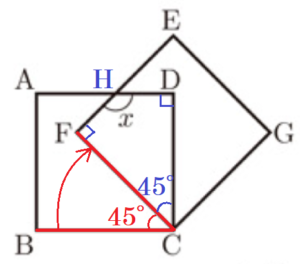
(11) 右の図のように,正方形 \( ABCD \),正方形 \( EFCG \) がある。正方形 \( ABCD \) を,点 \( C \) を中心として,時計まわりに \( 45° \) だけ回転移動させると,正方形 \( EFCG \) に重ね合わせることができる。このとき,\( ∠x \) の大きさを求めなさい。
【解説】
正方形 \( ABCD \) を \( 45° \) 回転移動させると
正方形 \( EFCG \) に重なるということは,
辺 \( BC \) を \( 45° \) 回転させたものが辺 \( FC \) になるので,\( ∠BCF=45° \)
正方形のすべての内角は \( 90° \) なので,
\( ∠DCF=∠BCD-∠BCF \)
\( =90°-45°=45° \)
\( =45° \)
よって,\( AD \) と \( EF \) の交点を \( H \) とすると,
四角形 \( CDHF \) において,
\( ∠x=360°-∠CFH-∠CDH-∠DCF \)
\( =360°-90°-90°-45° \)
\( =135° \)
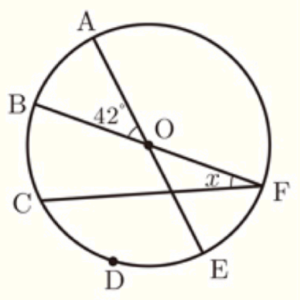
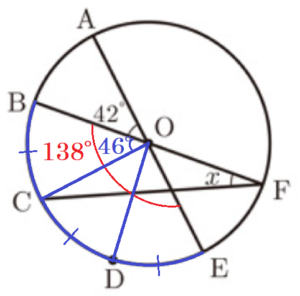
(12) 右の図で,6点 \( A,B,C,D,E,F \) は,円 \( O \) の周上の点であり,線分 \( AE \) と線分 \( BF \) は円 \( O \) の直径である。点 \( C \),点 \( D \) は弧 \( BE \) を3等分する点である。\( ∠AOB=42° \) のとき,\( ∠x \) の大きさを求めなさい。
【解説】
線分 \( AE \) は直径なので,\( ∠BOE=180°-42°=138° \)
弧 \( BC= \) 弧 \( CD= \) 弧 \( DE \) より,
\( ∠BOC=\dfrac{1}{3}∠BOE=46° \)
\( ∠BOC \) は,弧 \( BC \) の中心角,\( ∠x \) は,弧 \( BC \) の円周角なので,
\( ∠x=\dfrac{1}{2}∠BOC=23° \)
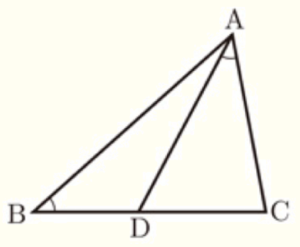
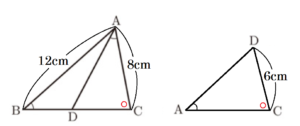
(13) 右の図のように,\( △ABC \) があり,点 \( D \) は辺 \( BC \) 上にある。
\( AB=12 \; cm,AC=8 \; cm,CD=6 \; cm,∠ABC=∠DAC \)
のとき,線分 \( AD \) の長さを求めなさい。
【解説】
\( △ABC \) と \( △DAC \) において,\( ∠ABC=∠DAC,∠C \)は共通 より,
2組の角がそれぞれ等しいので,\( △ABC \) ∽ \( △DAC \)
対応する辺の比は等しいので,
\( AB:AD=AC:CD \)
\( 12:AD=8:6 \)
\( 8AD=72 \)
\( AD=9 \; (cm) \)
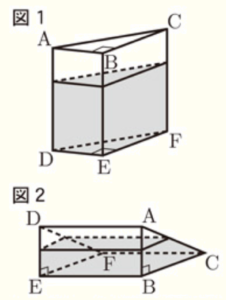
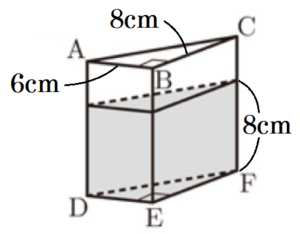
(14) 図1のように,三角柱 \( ABC-DEF \) の形をした透明な容器に水を入れて密閉した。この容器の側面はすべて長方形で,\( AB=6 \; cm,BC=8 \; cm,CF=12 \; cm,∠ABC=90° \) である。この容器を,\( △DEF \) が容器の底になるように,水平な台の上に置いた。このとき,容器の底から水面までの高さは \( 8 \; cm \) である。この容器を図2のように,四角形 \( FEBC \) が容器の底になるように,水平な台の上に置きかえたとき,容器の底から水面までの高さを求めなさい。 ただし,容器の厚みは考えないものとする。
【解答】
\( 6-2\sqrt{3} \; cm \)
【解説】
容器の置き方を変えても入っている水の量は同じであることを利用します。
図1の状態で容器に入っている水の体積を求めると,
\( \left(6 \times 8 \times \dfrac{1}{2} \right) \times 8=192 \; (cm^3) \)
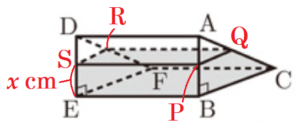
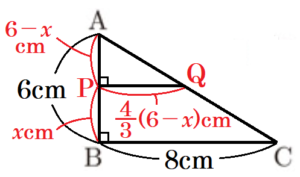
図2の状態での容器の底から水面までの高さを \( x \; cm \) とし,
水面の四すみの点をそれぞれ \( P,Q,R,S \) とすると,
このときの水の形状は,台形 \( BCQP \) を底面とした四角柱と考えることができます。
水面と面 \( FEBC \) は平行になるので,\( PQ//BC \) になっており,
\( △APQ \) ∽ \( △ABC \) となるので,
\( AP:AB=PQ:BC \)
\( 6-x:6=PQ:8 \)
\( PQ=\dfrac{4}{3}(6-x) \; (cm) \)
よって,台形 \( BCQP \)の面積は,
\( (PQ+BC) \times PB \times \dfrac{1}{2} \)
\( =\left\{\dfrac{4}{3}(6-x)+8 \right\} \times x \times \dfrac{1}{2} \)
\( =\left( 16-\dfrac{4}{3}x \right) \times x \times \dfrac{1}{2} \)
\( =-\dfrac{2}{3}x^2+8x \)
\( CF=12 \; cm \) なので,水の体積(\( =192 \; cm^3 \))は,
\( \left( -\dfrac{2}{3}x^2+8x \right) \times 12=192 \)
\( -8x^2+96x=192 \)
\( 8x^2-96x+192=0 \)
\( x^2-12x+24=0 \)
\( x=\dfrac{-(-12)±\sqrt{(-12)^2-4 \times 1 \times 24}}{2 \times 1} \)
\( =\dfrac{12±\sqrt{48}}{2} \)
\( =6±2\sqrt{3} \)
\( 0<x<6 \) より,あてはまるのは \( x=6-2\sqrt{3} \; (cm) \)
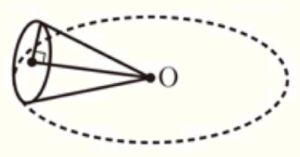
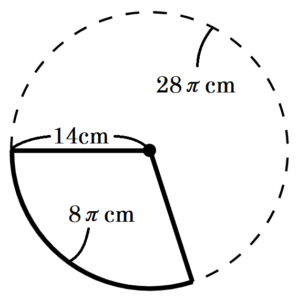
(15) 右の図のように,底面の半径が \( 4 \; cm \) の円錐を平面上に置き,頂点 \( O \) を中心としてすべらないように転がした。このとき,点線で表した円 \( O \) の上を1周し,もとの場所にもどるまでに3回半だけ回転した。この円錐の表面積を求めなさい。ただし,円周率を \( \pi \) とする。
【解説】
円すいを転がしたとき,円 \( O \) の上を1周したということは,
円 \( O \) の1周の長さと円すいの底面3周半の長さが等しくなるので,
円 \( O \) の周の長さは,
\( 2\pi \times 4 \times \left(3+\dfrac{1}{2} \right)=28\pi \; (cm) \)
このとき,円 \( O \) の半径を \( r \; cm \) とすると,
\( 2\pi \times r=28\pi \)
\( r=14 \; (cm) \)
円すいを展開したとき,おうぎ形の半径は円すいの母線の長さになり,
円すいの母線の長さと円 \( O \) の半径が等しいので,\( 14 \; cm \)
また,おうぎ形の弧の長さは,底面の円周の長さと等しくなるので,
\( 2\pi \times 4=8\pi \; (cm) \)
このおうぎ形は,半径 \( 14 \; cm \) の円(周の長さ \( 28\pi \; cm \) )から
弧の長さ \( 8\pi \; cm \) 分を切り取ったものと考えられるので,
おうぎ形の面積は,半径 \( 14 \; cm \) の円の面積の \( \dfrac{8\pi}{28\pi}=\dfrac{2}{7} \) 倍
以上より,円すいの表面積は,
\( \pi \times 4^2+\pi \times 14^2 \times \dfrac{2}{7} \)
\( =16\pi+56\pi \)
\( =72\pi \; (cm^2) \)
大問2
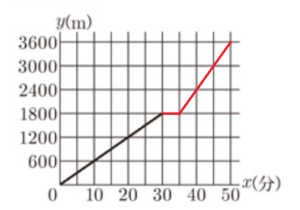
(1) 駅から \( 3600 \; m \) 離れた図書館まで,まっすぐで平らな道がある。健司さんは,午前 \( 10 \) 時に駅を出発し,毎分 \( 60 \; m \) の速さで図書館に歩いて向かった。駅から \( 1800 \; m \) 離れた地点で立ち止まって休憩し,休憩後は毎分 \( 120 \; m \) の速さで図書館に走って向かい,午前 \( 10 \) 時 \( 50 \) 分に図書館に着いた。次の図は,健司さんが駅を出発してから \( x \) 分後に駅から \( y \; m \) 離れた地点にいるとして,\( x \) と \( y \) の関係を表したグラフの一部である。
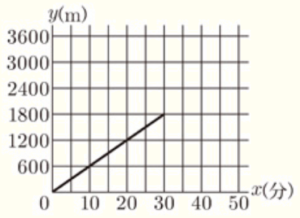
➀ 健司さんが駅から \( 1800 \; m \) 離れた地点で休憩を始めてから,図書館に着くまでの \( x \) と \( y \) の関係を表したグラフを図にかき加えなさい。
【解答・解説】
残りの \( 1800 \; m \) を毎分 \( 120 \; m \) の速さで走ったので,
かかった時間は,\( \dfrac{1800}{120}=15 \)(分)
よって,再出発した時間(休憩を終わった時間)は \( 50-15=35 \)(分後)
以上より,グラフは次のとおり
➁ 健司さんの姉の美咲さんは,健司さんが駅を出発した時刻と同じ時刻に,自転車に乗って図書館を出発し,毎分 \( 240 \; m \) の速さで駅に向かっていたところ,歩いて図書館に向かう健司さんと出会った。美咲さんと健司さんが出会ったときの時刻を求めなさい。
【解答】
午前 \( 10 \) 時 \( 12 \) 分
【解説】
美咲さんが,\( 3600 \; m \) の道のりを毎分 \( 240 \; m \) の速さで移動するのにかかる時間は,
\( \dfrac{3600}{240}=15 \)(分)なので,
これをグラフ中に書きたしてみると下のようになります。
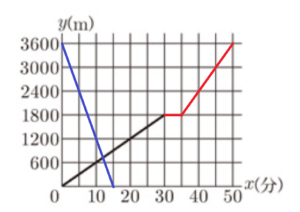
このグラフで黒の直線と青の直線の交点が2人が出会った時間と場所になります。
黒の直線の式は,\( y=60x \),青の直線の式は,\( y=-240x+3600 \) なので,
この2つの式を連立方程式として解くと,
\( 60x=-240x+3600 \)
\( 300x=3600 \)
\( x=12 \)
よって,出会った時刻は,午前 \( 10 \) 時 \( 12 \) 分
(2) 次の図のように,袋Aには整数 \( 1,2,3 \) が1つずつ書かれた3枚のカードが,袋Bには整数 \( 4,5,6 \) が1つずつ書かれた3枚のカードが入っている。このとき,下の ➀,➁ の問いに答えなさい。
➀ 袋A,袋Bからそれぞれカードを1枚ずつ取り出し,取り出されたカードに書かれている数の積を求める。このとき,積が奇数になる確率を求めなさい。ただし,袋Aからどのカードが取り出されることも,袋Bからどのカードが取り出されることも,それぞれ同様に確からしいものとする。
【解説】
偶数と奇数の組み合わせによって積が偶数,奇数どちらになるかを考えると,
偶数 \( \times \) 偶数 \( = \) 偶数
偶数 \( \times \) 奇数 \( = \) 偶数
奇数 \( \times \) 偶数 \( = \) 偶数
奇数 \( \times \) 奇数 \( = \) 奇数
となるので,積が奇数になるのは,袋A,袋B両方から奇数のカードを取り出したときです。
よって,積が奇数になる組み合わせは,\( (1,5),(3,5) \) の2通り
すべての場合の数は9通りなので,求める確率は,\( \dfrac{2}{9} \)

➁ 袋A,袋Bに入っているカードとは別に,整数 \( 7 \) が書かれているカードが6枚ある。袋Bに整数 \( 7 \) が書かれているカードを何枚か追加し,袋A,追加したカードが入っている袋Bからそれぞれカードを1枚ずつ取り出し,取り出されたカードに書かれている数の積を求める。積が奇数になる確率と積が偶数になる確率が等しいとき,追加したカードは何枚か,求めなさい。ただし,袋Aからどのカードが取り出されることも,追加したカードが入っている袋Bからどのカードが取り出されることも,それぞれ同様に確からしいものとする。
【解説】
積が奇数になる確率と積が偶数になる確率が等しいとき,積が奇数になる場合の数と積が偶数になる場合の数は等しくなるので,何枚のカードを追加したときにこれらの場合の数が等しくなるかを考えます。
追加したカードに \( 7A,7B,・・・ \) と名前をつけて樹形図に表すと,次のようになります。
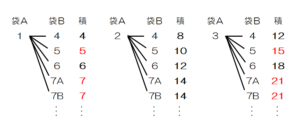
1枚追加したときは,積が奇数になる場合の数は2通り,積が偶数になる場合の数は1通り増えています。
2枚追加したときは,積が奇数になる場合の数は4通り,積が偶数になる場合の数は2通り増えています。
ここから,\( n \) 枚追加したときには ,積が奇数になる場合の数の方が \( n \) 通り多く増えているとわかります。
追加前には,積が奇数になる場合の数が2通り,積が偶数になる場合の数は7通りで,
偶数になる場合の方が5通り多かったので,5枚追加したときに奇数になる場合の数と偶数になる場合の数が等しくなります。
次のような表を書いてみるとわかりやすくなります。

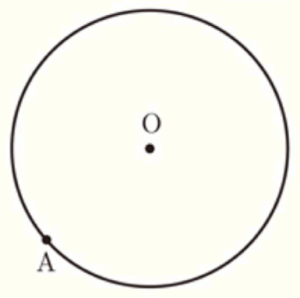
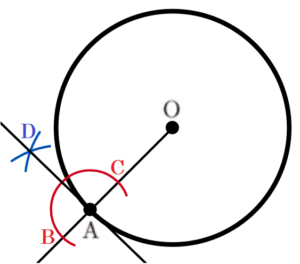
(3) 次の図のように,点 \( O \) を中心とする円の周上に点 \( A \) がある。このとき,点 \( A \) を接点とする円 \( O \) の接線を定規とコンパスを用いて作図しなさい。ただし,作図に用いた線は消さないこと。
【解答・解説】
円の接線は,接点と中心を通る直線と垂直に交わるので,
点 \( A \) を通り,直線 \( OA \) と垂直な直線が作図する接線になります。
手順1 直線 \( OA \) を描く
手順2 点 \( A \) を中心に円弧を描く
(直線 \( OA \) との交点を点 \( B,C \) とします)
手順3 点 \( B,C \) を中心に円弧を描く
(交点を点 \( D \) とします)
直線 \( AD \) が点 \( A \) を接点とする円 \( O \) の接線になります。
大問3
A中学校の図書委員会は,全校生徒を対象として,ある日曜日の読書時間を調査した。
次の (1)~(3) の問いに答えなさい。
(1) 図1のア~エは,3年1組を含む4つの学級の読書時間のデータを,ヒストグラムに表したものである。
例えば,アの10~20の階級では、読書時間が10分以上20分未満の生徒が1人いることを表している。4つの学級の生徒数は,すべて31人である。
3年1組のヒストグラムは,最頻値が中央値よりも小さくなる。3年1組のヒストグラムとして最も適切なものを、図1のア~エから1つ選んで記号を書きなさい。
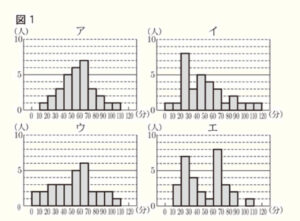
【解説】
最頻値 ・・・ 度数が最も大きいところの階級値
中央値 ・・・ データを順番に並べたとき,中央の位置にあたる値
(この問題では,16番目の値)
ア~エのヒストグラムで最頻値と中央値は次のとおりとなっています。
最頻値が中央値よりも小さくなっているのは イ
|
最頻値 |
中央値 |
| ア |
65 |
55 |
| イ |
25 |
45 |
| ウ |
65 |
55 |
| エ |
65 |
45 |
(2) 次の表は,3年2組30人の読書時間のデータを,小さい順に並べたものである。このデータの範囲と第1四分位数をそれぞれ求めなさい。
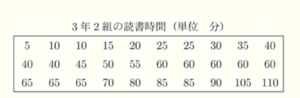
【解答】
範囲 ・・・ 105(分)
第1四分位数 ・・・ 30(分)
【解説】
範囲は,最大値 \( – \) 最小値 で求めることができます。
最大値は110(分),最小値5(分)なので,110-5=105(分)
第1四分位数は,前半分のデータの中央値になります。
この問題では,データの総数は30個なので,前半分は15個です。
この15個のデータに対する中央値は8番目の値になるので,30(分)
(3) 3年1組,2組,3組で運動部に所属している生徒は,16人ずついる。図2は,3年1組の運動部の生徒をグループ1,3年2組の運動部の生徒をグループ2,3年3組の運動部の生徒をグループ3とし,それぞれの読書時間のデータを,箱ひげ図に表したものである。
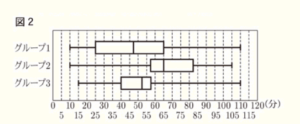
1 図2から読み取れることとして正しいものを,次のア~エからすべて選んで記号を書きなさい。
ア 読書時間が55分以下の生徒数が最も少ないグループは,グループ2である。
イ 読書時間が55分以上の生徒数が最も多いグループは,グループ3である。
ウ どのグループにも,読書時間が80分以上100分未満の生徒は必ずいる。
エ どのグループにも,読書時間が100分以上の生徒は必ずいる。
【解説】
アは正しい
グループ1 ・・・ 中央値が45分以上50分未満なので,55分以下の生徒数は少なくとも8人はいる。
グループ2 ・・・ 第1四分位数が55分以上60分未満なので,55分以下の生徒数は5人未満。
グループ3 ・・・ 中央値が50分以上55分未満なので,55分以下の生徒数は少なくとも8人はいる。
イは誤り
グループ1 ・・・ 中央値が45分以上50分未満なので,55分以上の生徒は8人未満。
グループ2 ・・・ 第1四分位数が55分以上60分未満なので,55分以上の生徒は少なくとも12人いる。
グループ3 ・・・ 中央値が50分以上55分未満なので,55分以上の生徒は8人未満。
ウは誤り
グループ1と3では,80分以上100分未満の範囲全体がひげの中に含まれています。
ひげにあたる範囲の中でどこにデータがあるかは箱ひげ図だけでは判断できません。
エは正しい
グループ1と3の最大値は110分,グループ2の最大値は105分なので,
100分以上の生徒は必ずいます。
2 図2において,読書時間のデータの散らばりぐあいが最も大きいグループを,次のア~ウから1つ選んで記号を書きなさい。
また,そのように判断した理由を,「範囲」と「四分位範囲」という両方の語句を用いて書きなさい。
ア グループ1 イ グループ2 ウ グループ3
【解答】
ア
範囲,四分位数がどちらもグループ1が最も大きい
【解説】
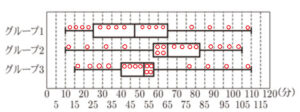
左右のひげと箱の左側と右側には同じ数のデータが含まれます。
この問題の場合,データの総数が16個なので,各部分に4個ずつのデータが含まれます。
例として各部分に含まれるデータを○で表すと下の図のようになり,
ひげや箱の長さが短いときはデータが密集し,長いときはデータが散らばっていることがわかります。
大問4
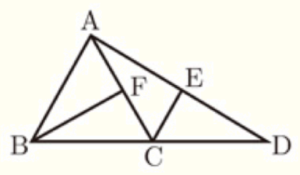
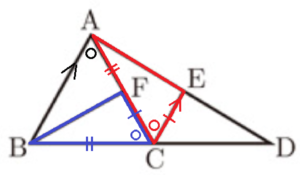
(1) 図のように,正三角形 \( ABC \) がある。点 \( D \) は辺 \( BC \) を \( C \) の方向に延長した直線上にある。点 \( E \) は線分 \( AD \) 上にあり,\( AB//EC \) である。点 \( F \) は辺 \( AC \) 上にあり,\( CE=CF \) である。このとき,\( △ACE≡△BCF \) となることを証明しなさい。
【解答】
\( △ACE \) と \( △BCF \) において,
\( AB//EC \) より,\( ∠BAC=∠ACE \) ・・・ ➀
\( △ABC \) は正三角形なので,
\( ∠BAC=∠BCF \) ・・・ ➁
\( AC=BC \) ・・・ ➂
➀➁より,\( ∠ACE=∠BCF \) ・・・ ➃
仮定より,\( CE=CF \) ・・・ ➄
➂➃➄より,2組の辺とその間の角がそれぞれ等しいので,
\( △ACE≡△BCF \)
(2) 詩織さんは,次のことがらの逆について考えたことをまとめた。〔詩織さんのメモ〕が正しくなるように,アには記述の続きを,イには反例を書きなさい。
2つの自然数 \( a,b \) において,\( a=3,b=6 \) ならば,\( a+b=9 \)
〔詩織さんのメモ〕
逆は,次のようにいえる。
2つの自然数a,b において, ア
逆は,正しくない。(反例) イ
【解答】
ア ・・・ \( a+b=9 \) ならば,\( a=3,b=6 \)
イ ・・・ \( a=4,b=5 \)
【解説】
A ならば
B ということがらにおいて,
A を仮定,
B を結論といいます。
そして,仮定と結論を入れ替えたものを「逆」といいます。
この例でいうと,
B ならば
A になります。
また, A ならば B ということがらにおいて,
仮定は成り立つが,結論は成り立たない実例のことを反例といいます。
例えば,「ほ乳類であるならば,人間である」ということがらに対して,
犬,猫,馬 などは,ほ乳類ではあるが人間ではないので,これらが反例になります。
この問題では,\( a=3,b=6 \) が仮定,\( a+b=9 \) が結論になるので,
その逆は,\( a+b=9 \) ならば,\( a=3,b=6 \) になり,
\( a+b=9 \) になるのは,\( a=4,b=5 \),\( a=2,b=7 \) などの場合もあるので,
これらが反例になります。
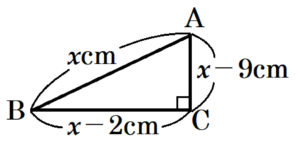
(3) 直角三角形 \( ABC \) で,辺 \( AB \) の長さは,辺 \( BC \) の長さより \( 2 \; cm \) 長く,辺 \( BC \) の長さは辺 \( CA \) の長さより \( 7 \; cm \) 長い。このとき,直角三角形 \( ABC \) の斜辺の長さを求めなさい。
【解説】
辺 \( AB \) の長さは,辺 \( BC \) の長さより \( 2 \; cm \) 長いので,\( AB=BC+2 \) ・・・ ➀
辺 \( BC \) の長さは辺 \( CA \) の長さより \( 7 \; cm \) 長いので,\( BC=CA+7 \) ・・・ ➁
➀➁より,3辺の長さの関係は,\( AB>BC>CA \) になっています。
直角三角形において,一番長い辺が斜辺になるので,
辺 \( AB \) が斜辺になります。
辺 \( AB \) の長さを \( x \; cm \) とすると,
➀より,\( BC=x-2 \; cm \)
➁より,\( CA=x-2-7=x-9 \; cm \)
よって,三平方の定理より,
\( (x-2)^2+(x-9)^2=x^2 \)
\( x^2-4x+4+x^2-18x+81=x^2 \)
\( x^2-22x+85=0 \)
\( (x-5)(x-17)=0 \)
\( x=5,17 \)
\( x-9>0 \) より \( x>9 \) なので,あてはまるのは,\( x=17 \; (cm) \)
大問5
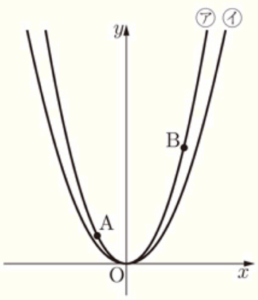
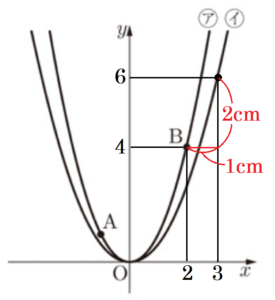
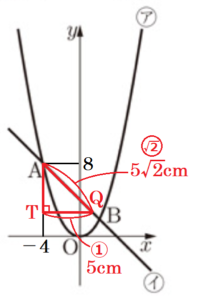
Ⅰ 次の図において,ア は関数 \( y=x^2 \),イ は関数 \( y=ax^2 \; (0<a<1) \) のグラフである。2点 \( A,B \) は,ア 上の点であり,点 \( A \) の座標は \( (-1,1) \),点Bの座標は \( (2,4) \) である。原点 \( O \) から \( (0,1),(1,0) \) までの距離を,それぞれ \( 1 \; cm \) とする。次の (1)~(3) の問いに答えなさい。
(1) 2点 \( A,B \) を通る直線の式を求めなさい。求める過程も書きなさい。
【解答】
\( A(-1,1),B(2,4) \) を通るので,直線 \( AB \) の傾きは,
\( \dfrac{4-1}{2-(-1)}=1 \)
直線 \( AB \) の式を \( y=x+b \) とすると,\( (2, 4) \) を通るので,
\( 4=2+b \)
\( b=2 \)
よって,直線 \( AB \) の式は \( y=x+2 \)
(2) \( a=\dfrac{2}{3} \) のとき,イ 上に,\( x \) 座標が \( 3 \) である点 \( C \) をとる。このとき,線分 \( BC \) の長さを求めなさい。
【解答】
\( \sqrt{5} \; cm \)
【解説】
点 \( C \) は,\( y=\dfrac{2}{3}x^2 \) 上の点で,\( x \) 座標が \( 3 \) なので,
点 \( C \) の \( y \) 座標は,\( y=\dfrac{2}{3} \times 3^2=6 \)
よって,三平方の定理より,
\( BC^2=(3-2)^2+(6-4)^2=5 \)
\( BC=\sqrt{5} \; (cm) \) (\( BC>0 \)より)
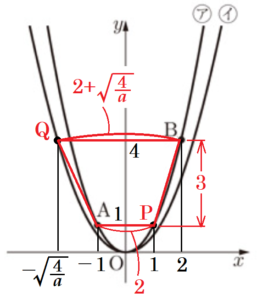
(3) ア 上に,\( x \) 座標が正で,\( y \) 座標が \( 1 \) である点 \( P \) をとる。イ 上に,\( x \) 座標が \( -1 \) より小さく,\( y \) 座標が \( 4 \) である点 \( Q \) をとる。四角形 \( APBQ \) の面積が \( 12 \; cm^2 \) になるとき,\( a \) の値を求めなさい。
【解答】
\( a=\dfrac{1}{4} \)
【解説】
点 \( P \) は,\( y=x^2 \) 上の点で,\( y \) 座標が \( 1 \) なので,
点 \( P \) の \( x \) 座標は,
\( 1=x^2 \)
\( x=1 \) (\( x>0 \)より)
点 \( Q \) は,\( y=ax^2 \) 上の点で,\( y \) 座標が \( 4 \) なので,
点 \( Q \) の \( x \) 座標は,
\( 4=ax^2 \)
\( x=-\sqrt{\dfrac{4}{a}} \) (\( x<-1,0<a<1 \)より)
このとき,
\( AP=1-(-1)=2 \),
\( BQ=2-\left(-\sqrt{\dfrac{4}{a}} \right)=2+\sqrt{\dfrac{4}{a}} \)
であり,四角形 \( APBQ \) は台形なので,
\( \left(2+2+\sqrt{\dfrac{4}{a}} \right) \times 3 \times \dfrac{1}{2}=12 \)
\( 4+\sqrt{\dfrac{4}{a}}=8 \)
\( \sqrt{\dfrac{4}{a}}=4 \)
\( \dfrac{4}{a}=16 \)
\( a=\dfrac{1}{4} \)
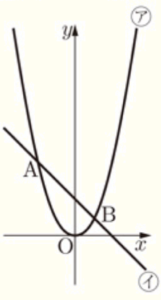
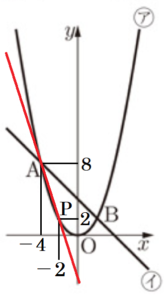
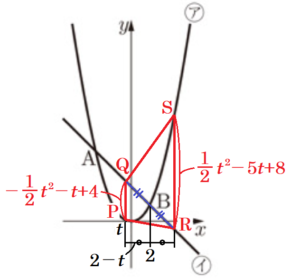
Ⅱ 次の図において,ア は関数 \( y=\dfrac{1}{2}x^2 \),イ は関数 \( y=-x+4 \) のグラフであり,点 \( A \) の座標は \( (-4,8) \),点 \( B \) の座標は \( (2,2) \) である。ア 上に,\( x \) 座標が \( t \) である点 \( P \) をとり,イ 上に,点 \( P \) と \( x \) 座標が等しい点 \( Q \) をとる。原点 \( O \) から \( (0,1),(1,0) \) までの距離を,それぞれ \( 1 \; cm \) とする。次の (1),(2) の問いに答えなさい。
(1) \( t=-2 \) のとき,2点 \( A,P \) を通る直線の式を求めなさい。求める過程も書きなさい。
【解答】
点 \( P \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,\( x \) 座標が \( -2 \) なので,
\( y \) 座標は,\( y=\dfrac{1}{2} \times (-2)^2=2 \)
よって,直線 \( AP \) は,\( A(-4,8),P(-2,2) \) を通るので,
傾きは,\( \dfrac{2-8}{-2-(-4)}=-3 \)
直線 \( AP \) の式を \( y=-3x+b \) とすると,\( (-2,2) \) を通るので,
\( 2=-3 \times (-2)+b \)
\( b=-4 \)
よって,直線 \( AP \) の式は \( y=-3x-4 \)
(2) \( -4<t<2 \) とする。
1 \( AQ=5\sqrt{2} \; cm \) になるとき,\( t \) の値を求めなさい。
【解説】
点 \( A \) を通り,\( y \) 軸と平行な直線と,点 \( Q \) を通り,
\( x \) 軸と平行な直線の交点を点 \( T \) とすると,
イ の直線の式が \( y=-x+4 \) であることから,
\( △AQT \) は \( AQ \) を斜辺とする直角二等辺三角形になっています。
よって,\( QT=\dfrac{1}{\sqrt{2}}AQ=5 \; (cm) \)
点 \( T \) の \( x \) 座標は \( -4 \)で,
点 \( Q \) の \( x \) 座標は \( -4 \) より大きいので,
\( t=-4+5=1 \)
2 イ 上に,\( x \) 座標が \( 2 \) より大きい点 \( R \) を,線分 \( BR \) の長さと線分 \( BQ \) の長さが等しくなるようにとる。ア上に,点 \( R \) と \( x \) 座標が等しい点 \( S \) をとる。四角形 \( PQSR \) の面積が \( 30 \; cm^2 \) になるとき,\( t \) の値を求めなさい。
【解説】
点 \( P,Q \) の \( x \) 座標が \( t \) であることから,
点 \( P \) の \( y \) 座標は,\( y=\dfrac{1}{2}t^2 \)
点 \( Q \) の \( y \) 座標は,\( y=-t+4 \)
と表せるので,
\( PQ=(-t+4)-\dfrac{1}{2}t^2=-\dfrac{1}{2}t^2-t+4 \; (cm) \)
点 \( R \) は \( BQ=BR \) となる点で,
点 \( B \) の \( x \) 座標が点 \( Q \) の \( x \) 座標より
\( 2-t \) だけ大きいことから,
点 \( R \) の \( x \) 座標は \( 2+(2-t)=4-t \)
点 \( R,S \) の \( x \) 座標が \( 4-t \) であることから,
点 \( R \) の \( y \) 座標は,\( y=-(4-t)+4=t \)
点 \( S \) の \( y \) 座標は,\( y=\dfrac{1}{2}(4-t)^2 \)
と表せるので,
\( RS=\dfrac{1}{2}(4-t)^2-t=\dfrac{1}{2}t^2-5t+8 \; (cm) \)
\( PQ//RS \) であることから,四角形 \( PQSR \) は台形であり,高さは \( 2(2-t)=4-2t \; (cm) \) なので,
四角形 \( PQSR \) の面積を表す方程式は,
\( \left\{\left(-\dfrac{1}{2}t^2-t+4\right)+\left(\dfrac{1}{2}t^2-5t+8\right)\right\} \times (4-2t) \times \dfrac{1}{2}=30 \)
\( (-6t+12)(2-t)=30 \)
\( 6(t-2)^2=30 \)
\( (t-2)^2=5 \)
\( t-2=±\sqrt{5} \)
\( t=2±\sqrt{5} \)
\( -4<t<2 \) より,あてはまるのは,\( t=2-\sqrt{5} \)