大問１
（１） \( 6-2 \times 5 \) を計算しなさい。
（２） \( 5(x+2y)-2(4x-y) \) を計算しなさい。
（３） \( 90 \) を素因数分解しなさい。
（４） \( x=3，y=-2 \) のとき，\( \dfrac{1}{3}x^2y^3 \div 2xy \) の値を求めなさい。
（５） \( \sqrt{32}-\sqrt{50}+\sqrt{27} \) を計算しなさい。
（６） 方程式 \( 0.8x+4=1.5x-0.9 \) を解きなさい。
（７） 連立方程式 \( \left\{ \begin{array}{}
2x-y=7 \\
5x+3y=1 \\
\end{array} \right. \) を解きなさい。
（８） 方程式 \( x^2-2x=24 \) を解きなさい。
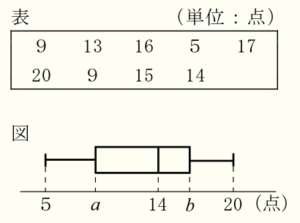
（９） 右の表は，クイズ大会に参加した９人の得点である。
表をもとにして，箱ひげ図をかくと，右の図のようになった。
\( a，b \) の値を求めなさい。
（１０） \( n^2-20n+91 \) の値が素数になる自然数 \( n \) をすべて求めなさい。
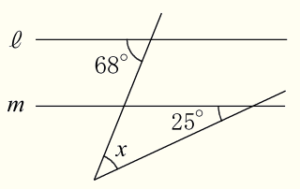
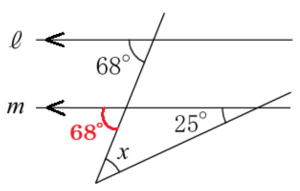
（１１） 右の図で，２直線 ℓ，\( m \) は平行である。このとき，\( ∠x \) の大きさを求めなさい。
平行線の同位角は等しいことから，
下の三角形の外角が \( 68° \) になるので，
\( ∠x+25°=68° \)
\( ∠x=43° \)
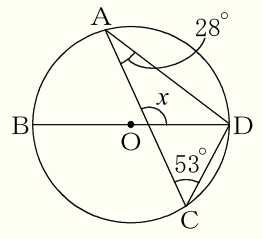
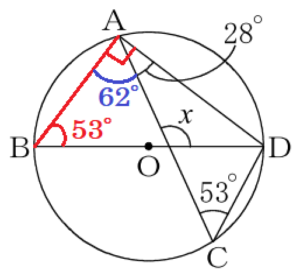
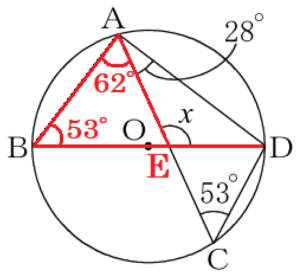
（１２） 右の図で，４点 \( A，B，C，D \) は円 \( O \) の周上の点であり，線分 \( BD \) は円 \( O \) の直径である。\( ∠CAD=28°， ∠ACD=53° \) のとき，\( ∠x \) の大きさを求めなさい。
補助線 \( AB \) をひくと，
弧 \( AD \) の円周角なので，\( ∠ABD=∠ACD=53° \)
直径に対する円周角なので，\( ∠BAD=90° \)
\( ∠BAC=∠BAD-∠DAC \) なので，\( ∠BAC=90°-28°=62° \)
線分 \( AC \) と線分 \( BD \) の交点を点 \( E \) とすると，
\( ∠x \) は \( △ABE \) の外角なので，
\( ∠x=53°+62°=115° \)
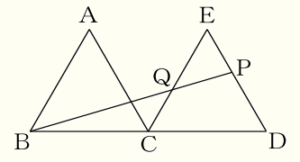
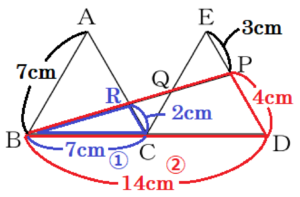
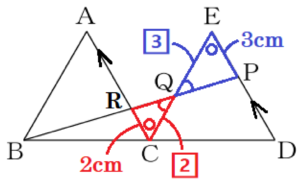
（１３） 右の図のように，\( △ABC \) と \( △ECD \) は合同な正三角形であり，点 \( B，C，D \) は一直線上にある。点 \( P \) は辺 \( DE \) 上の点であり，点 \( Q \) は線分 \( BP \) と辺 \( CE \) の交点である。\( AB=7 \; cm \)，\( EP=3 \; cm \) のとき，線分 \( CQ \) の長さを求めなさい。
線分 \( BP \) と辺 \( AC \) の交点を点 \( R \) とすると，
\( △BCR \) ∽ \( △BDP \) であり，
\( CR：DF=BC：BD \)
\( CR：4=7：14 \)
\( CR=2 \; (cm) \)
また，\( △QCR \) ∽ \( △QEP \) であり，
\( CR：EP=2：3 \) なので，\( CQ：EQ=2：3 \)
よって，
\( CQ=\dfrac{2}{5}CE=\dfrac{14}{5} \; (cm) \)
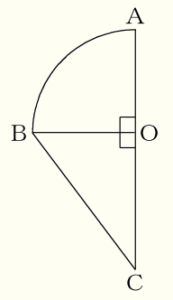
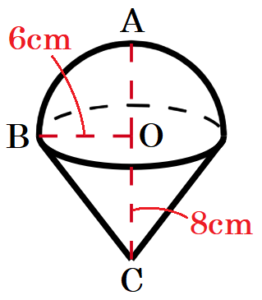
（１４） 右の図のように, おうぎ形 \( AOB \) と直角三角形 \( BOC \) が同平面上にあり，\( OB=6 \; cm，BC=10 \; cm，∠AOB=90° \)，
\( ∠BOC=90° \) である。 おうぎ形 \( AOB \) と直角三角形 \( BOC \) を合わせた図形を，直線 \( AC \) を軸として１回転させてできる立体の体積を求めなさい。ただし，円周率を \( \pi{} \) とする。
\( OB=6 \; cm，BC=10 \; cm \) より，
直角三角形 \( BOC \) は，３辺の長さが \( 3：4：5 \) になっているので，\( OC=8 \; cm \) です。
ここから，回転させてできる立体は，
半径 \( 6 \; cm \) の半球と底面の半径 \( 6 \; cm \)，高さ \( 8 \; cm \) の円すい
をくっつけたものになります。
半径 \( 6 \; cm \) の半球の体積は，
\( \dfrac{4}{3}\pi{} \times 6^3 \times \dfrac{1}{2}=144\pi{} \; (cm^3) \)
底面の半径 \( 6 \; cm \)，高さ \( 8 \; cm \) の円すいの体積は，
\( \pi{} \times 6^2 \times 8 \times \dfrac{1}{3}=96\pi{} \; (cm^3) \)
よって，求める立体の体積は，
\( 144\pi{}+96\pi{}=240\pi{} \; (cm^3) \)
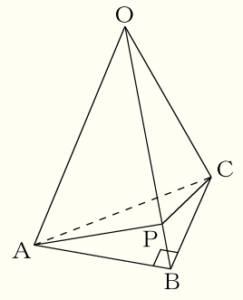
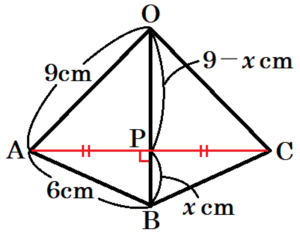
（１５） 右の図のように，三角錐 \( OABC \) がある。\( △ABC \) は直角二等辺三角形で， \( AB=BC=6 \; cm，∠ABC=90° \) である。
また，\( OA =OB=OC=9 \; cm \) である。点 \( A \) から辺 \( OB \) を通り，点 \( C \) まで最も短くなるようにひいた線と辺 \( OB \) の交点を \( P \) とする。このとき，三角錐 \( PABC \) の体積を求めなさい。
面 \( OAB \) と面 \( OBC \) を展開すると，
３点 \( A，P，C \) は一直線上に並び，
点 \( P \) は，線分 \( AC \) の中点，
\( AC⊥OB \)
になります。
ここで，\( BP=x \; cm \) とすると，
\( 9^2-(9-x)^2=6^2-x^2 \)
\( 18x-x^2=36-x^2 \)
\( x=2 \; (cm) \)
このとき，線分 \( AP \) の長さは，
\( AP^2=6^2-2^2=32 \)
\( AP=4\sqrt{2} \; (cm) \)
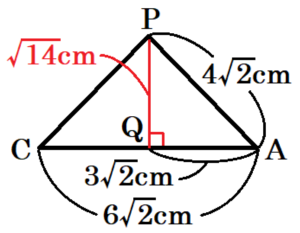
三角錐 \( PABC \) の底面を \( △APC \) とすると，
\( △APC \) は，\( AP=AC=4\sqrt{2} \; cm \)，\( AC=6\sqrt{2} \; cm \) の二等辺三角形になっています。
点 \( P \) から辺 \( AC \) に垂線をひき，
交点を点 \( Q \) とすると，
\( AP=4\sqrt{2} \; cm，AQ=3\sqrt{2} \; cm \) なので，
\( PQ^2=(4\sqrt{2})^2-(3\sqrt{2})^2=14 \)
\( PQ=\sqrt{14} \; (cm) \)
以上より，三角錐 \( PABC \) の体積は，
\( \left( 6\sqrt{2} \times \sqrt{14} \times \dfrac{1}{2} \right) \times 2 \times \dfrac{1}{3}=4\sqrt{7} \; (cm^3) \)
大問２
（１） バスケットボールの試合で，Ａ選手は２点シュートと３点シュートを合わせて１０本決めた。この試合で，Ａ選手の得点の合計は２３点だった。健司さんと美咲さんは，Ａ選手が２点シュートと３点シュートをそれぞれ何本決めたか求めるために，健司さんは１つの文字，美咲さんは２つの文字を用いて，方程式をつくった。２人のメモが正しくなるように，\( \fbox{ ア }，\fbox{ イ } \) にあてはまる式を書きなさい。
２点シュートを \( x \) 本決めたとすると，３点シュートは \( \fbox{ ア } \) 本決めたことになるから，
次の１次方程式ができる。
\( 2x+3(\;\fbox{ ア }\;)=23 \)
２点シュートを \( x \) 本，３点シュートを \( y \) 本決めたとすると，
次の連立方程式ができる。
\( \left\{ \begin{array}{}
x+y=10 \\
\fbox{ イ }=23 \\
\end{array} \right. \)
（２） 次の①，②の問いに答えなさい。
① 関数 \( y=\dfrac{1}{2}x^2 \) で，\( x \) の変域が \( -2≦x≦a \) のとき，\( y \) の変域は \( b≦y≦18 \) である。このとき，\( a，b \) の値を求めなさい。
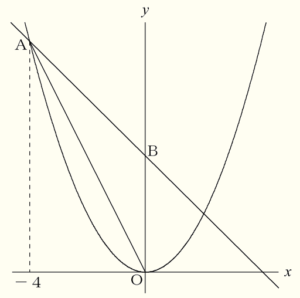
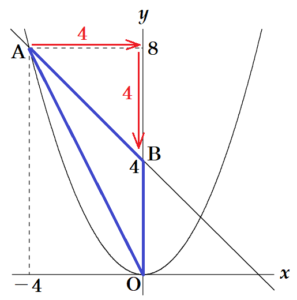
② 次の図のように，関数 \( y=\dfrac{1}{2}x^2 \) のグラフ上に，\( x \) 座標が \( -4 \) である点 \( A \) をとる。点 \( A \) を通り，傾きが \( -1 \) である直線と \( y \) 軸の交点を \( B \) とするとき，\( △AOB \) の面積を求めなさい。ただし，原点 \( O \) から \( (0，1)，(1，0) \) までの距離を，それぞれ \( 1 \; cm \) とする。
点 \( A \) は，\( y=\dfrac{1}{2}x^2 \) 上の点で，
\( x=-4 \) 座標の値は \( -4 \) なので，\( y \) 座標の値は，
\( y=\dfrac{1}{2} \times (-4)^2=8 \)
ここから，点 \( A \) の座標は \( A(-4，8) \)
直線 \( AB \) の傾きは \( -1 \) であり，
点 \( B \) は，点 \( A \) から \( x \) 座標の値が \( 4 \) 増えた座標なので，点 \( B \) の \( y \) 座標の値は，
点 \( A \) から \( 4 \) 減った座標になります。
よって，点 \( B \) の座標は \( B(0，4) \)
以上より，\( △AOB \) の面積は，
\( 4 \times 4 \times \dfrac{1}{2}=8 \; (cm^2) \)
(3) 次の表は，ある学級２０人のハンドボール投げの記録を度数分布表にまとめたものである。
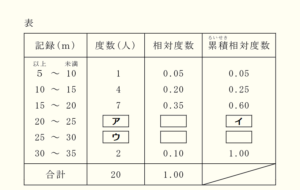
➀ \( \fbox{ イ } \) にあてはまる数が \( 0.70 \) 以下のとき，\( \fbox{ ア } \) にあてはまる数をすべて求めなさい。
➁ この学級の記録の最頻値は，\( \fbox{ ア } \) と \( \fbox{ ウ } \) に入る数にかかわらず，\( 15 \; m \) 以上 \( 20 \; m \) 未満の階級の階級値 \( 17.5 \; m \) であることがわかる。 その理由を，「度数」の語句を用いて書きなさい。
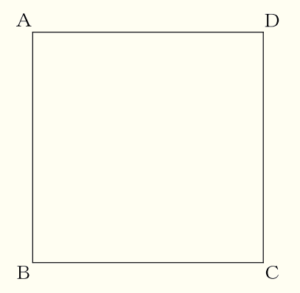
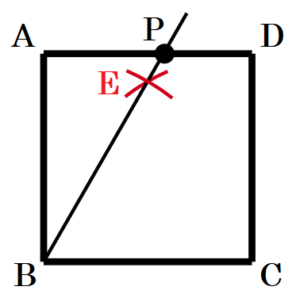
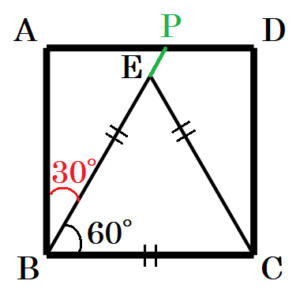
（４） 図のような正方形 \( ABCD \) がある。辺 \( AD \) 上に，
\( ∠ABP=30° \) となる点 \( P \) を定規とコンパスを用いて作図しなさい。 ただし，作図に用いた線は消さないこと。
手順１ 点 \( B，C \) を中心に辺 \( BC \) を半径とする
円弧を描く
（交点を点 \( E \) とします）
手順２ ２点 \( B，E \) を通る直線を描く
手順２の直線と辺 \( AD \) 交点が
求める点 \( P \) になります。
\( ∠ABP=30° \) のとき，\( ∠CBP=60° \) になります。
正三角形の内角は \( 60° \) なので，
辺 \( BC \) を１辺とする正三角形 \( BCE \) を描くと，
\( 60° \) の角ができます。
この辺 \( BE \) を辺 \( AD \) まで延長すると，
求める点 \( P \) になります。
大問３
守さんと香さんは，新聞記事をきっかけに，トラックが走る距離と燃料の量に関心をもち，その関係を調べることにした。[メモ]は，３台のトラック（Ａ車，Ｂ車，Ｃ車）それぞれについて，走る距離と燃料の量の関係をまとめたものである。ただし，３台のトラックは，それぞれ \( 1 \; L \) あたり一定の距離を走り、燃料タンクの燃料をすべて使いきることができるものとする。
Ａ車
・ \( 1 \; L \) あたり \( 10 \; km \) 走る。
・ 燃料タンクの容量は \( 70 \; L \) である。
Ｂ車
・ \( 1 \; L \) あたり \( 4 \; km \) 走る。
・ 燃料タンクいっぱいに燃料を入れて出発すると， \( 400 \; km \) 走ったときの燃料タンクに残っている
燃料の量は \( 0 \; L \) になる。
Ｃ車
・ 燃料タンクの容量は \( 230 \; L \) である。
・ 燃料タンクいっぱいに燃料を入れて出発すると，\( 150 \; km \) 走ったときの燃料タンクに残っている
燃料の量は \( 170 \; L \) になる。
（１） 守さんは，Ａ車とＢ車それぞれについて，\( x \; L \) の燃料を使用したときの走った距離を \( y \; km \) とし，\( y \) は \( x \) に比例するとみなして図１のグラフをかいた。 点 \( P \) はＡ車のグラフ上の点であり，点 \( Q，R \) はＢ車のグラフ上の点である。点 \( P，Q \) の \( x \) 座標は等しく，点 \( R \) の \( x \) 座標は \( 6 \) である。
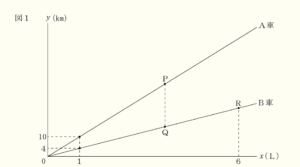
① 点 \( R \) の \( y \) 座標を求めなさい。
➁ 図１で，線分 \( PQ \) の長さが表すこととして正しいものを，次のア～エから１つ選んで記号を書きなさい。
ア 同じ距離を走ったときの，Ａ車とＢ車それぞれが使用した燃料の量の和
イ 同じ距離を走ったときの，Ａ車とＢ車それぞれが使用した燃料の量の差
ウ 同じ量の燃料を使用したときの，Ａ車とＢ車それぞれが走った距離の和
エ 同じ量の燃料を使用したときの，Ａ車とＢ車それぞれが走った距離の差
（２） 香さんは，燃料タンクいっぱいに燃料を入れて出発したＡ車とＢ車それぞれが，途中で燃料を追加せずに，\( x \; km \) 走ったときの燃料タンクに残っている燃料の量を \( y \; L \) として考えた。香さんは，\( y \) は \( x \) の１次関数であるとみなして図２のグラフをかいた。点 \( S \) は，Ａ車のグラフとＢ車のグラフの交点である。
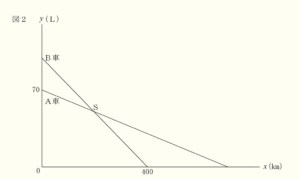
香さんは，交点 \( S \) からわかることを，次のように説明した。【香さんの説明】が正しくなるように， ア にはあてはまる式を， イ 〜 エ にはあてはまる数を書きなさい。
[メモ]から，\( 1 \; km \) 走るごとにＡ車は \( \dfrac{1}{10} \; L \)，Ｂ車は \( \dfrac{1}{4} \; L \) の燃料を使います。
Ａ車とＢ車それぞれについて，\( y \) を \( x \) の式で表すと，
Ａ車の式は \( y=-\dfrac{1}{10}x+70 \) ･･･ ➀
Ｂ車の式は \( y = \) ア ･･･ ➁ となります。
➀，➁を連立方程式として解くと，交点 \( S \) の座標は \( ( \) イ ， ウ \( ) \) となります。
このことから，Ａ車とＢ車それぞれが， イ \( km \) 走ったときの燃料タンクに残っている燃料の量は
どちらも ウ \( L \) であることがわかります。
また，Ａ車は イ \( km \) 走ったとき，燃料を エ \( L \) 使ったことがわかります。
（３） 燃料タンクいっぱいに燃料を入れて出発したＡ車とＣ車それぞれが，途中で燃料を追加せずに \( 550 \; km \) 走った。このとき，燃料タンクに残っている燃料の量は，どちらの車のほうが何 \( L \) 多いか，求めなさい。求める過程も書きなさい。ただし，次の【考え方】のどちらかを ○ で囲み，その考え方に沿って書くこと。
【考え方】
守さんの考え方
Ａ車とＣ車それぞれについて，\( x \; L \) の燃料を使用したときの走った距離を \( y \; km \) とし，
\( y \) は \( x \) に比例するとみなす。
香さんの考え方
Ａ車とＣ車それぞれについて，\( x \; km \) 走ったときの燃料タンクに残っている燃料の量を \( y \; L \) とし，
\( y \) は \( x \) の１次関数であるとみなす。
大問４
（１） 図１のように, 縦, 横それぞれ３マスずつのマス目と矢印が印刷されているたくさんの用紙と，１から順に自然数が１つずつ書かれているカードがある。図２のように，用紙の向きを変えずに，１枚目の用紙には \( \fbox{1} \) から順に中央のマスから矢印に沿ってカードを並べていく。２枚目の用紙には \( \fbox{10} \) から順に，３枚目の用紙には \( \fbox{19} \) から順に，同様にカードを並べていく。４枚目以降の用紙にも同様にカードを並べていくものとする。
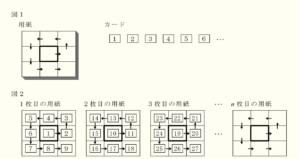
➀ ５枚目の用紙で，中央のマスにあるカードに書かれている数を求めなさい。
➁ \( n \) 枚目の用紙で，中央のマスの左上のマスにあるカードに書かれている数を，\( n \) を用いた式で表しなさい。
（２） １から６までの目が出るさいころを投げる。ただし，さいころのどの目が出ることも同様に確からしいものとする。
① このさいころを１回投げて出た目を \( a \) とする。\( a+3 \) の値が４の倍数になる確率を求めなさい。
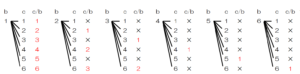
➁ このさいころを２回投げたとき，１回目に出た目を \( b \)，２回目に出た目を \( c \) とする。
\( \dfrac{c}{b} \) の値が整数になる確率を求めなさい。
整数になる組み合わせは１４通り，すべての組み合わせは３６通りなので，
求める確率は，\( \dfrac{14}{36}=\dfrac{7}{18} \)
大問５
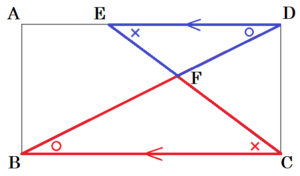
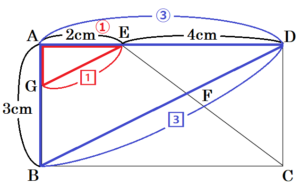
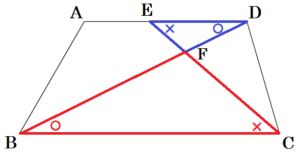
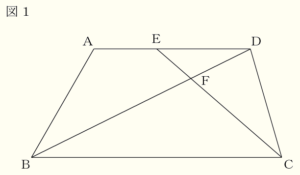
Ⅰ 図１において，四角形 \( ABCD \) は長方形である。点 \( E \) は辺 \( AD \) 上の点であり，点 \( F \) は線分 \( BD \) と線分 \( CE \) の交点である。 次の（１），（２）の問いに答えなさい。
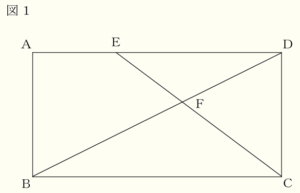
（１） \( △FBC \) ∽ \( △FDE \) となることを証明しなさい。
\( △FBC \) と \( △FDE \) において，
長方形の向かい合う辺は平行なので，
\( AD//BC \) であり，
錯角は等しいので，
\( ∠FBC=∠FDE \) ･･･ ➀
\( ∠FCB=∠FED \) ･･･ ➁
➀➁より，２組の角がそれぞれ等しいので，
\( △FBC \) ∽ \( △FDE \)
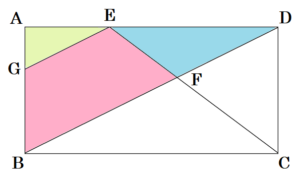
（２） 図２は，図１に点 \( E \) を通り線分 \( BD \) に平行な直線をかき加え，辺 \( AB \) との交点を \( G \) としたものである。\( AB=3 \; cm， AE=2 \; cm，ED=4 \; cm \) とする。
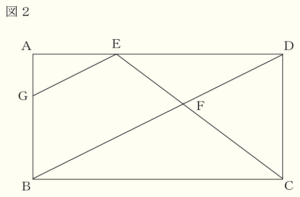
① 線分 \( EG \) の長さを求めなさい。
\( △AGE \) ∽ \( △ABD \) なので，
\( EG：DB=AE：AD=1：3 \)
\( △ABD \) において，三平方の定理より，
\( DB^2=3^2+6^2=45 \)
\( DB=3\sqrt{5} \; (cm) \)
よって，
\( EG：3\sqrt{5}=1：3 \)
\( EG=\sqrt{5} \; (cm) \)
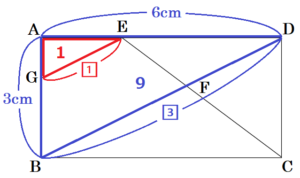
➁ 四角形 \( GBFE \) の面積を求めなさい。
四角形 \( GBFE \) の面積を直接求めるのは手間がかかるので，
\( △ABD-△AGE-△FDE \) で求めます。
問➀より，\( △AGE \) と \( △ABD \) の相似比は
\( 1：3 \) なので，面積比は \( 1^2：3^2=1：9 \) であり，
\( △AGE=\dfrac{1}{9}△ABD \)
\( △ABD \) の面積は
\( 6 \times 3 \times \dfrac{1}{2}=9 \; (cm^2) \) ･･･（ア）
\( △AGE \) の面積は
\( \dfrac{1}{9}△ABD=1 \; (cm^2) \) ･･･（イ）
\( △FDE \) と \( △FBC \) において，
点 \( F \) から辺 \( AD，BC \) に垂線をひき，
交点をそれぞれ点 \( H，I \) とすると，
\( △FDE \) ∽ \( △FBC \) なので，
\( FH：FI=DE：BC=2：3 \)
\( HI=AB=3 \; cm \) なので，
\( FH=\dfrac{2}{5}HI=\dfrac{6}{5} \; (cm) \)
\( △FDE \) の面積は
\( 4 \times \dfrac{6}{5} \times \dfrac{1}{2}=\dfrac{12}{5} \; (cm^2) \) ･･･（ウ）
（ア）（イ）（ウ）より，四角形 \( GBFE \) の面積は，
\( △ABD-△AGE-△FDE=9-1-\dfrac{12}{5}=\dfrac{28}{5} \; (cm^2) \)
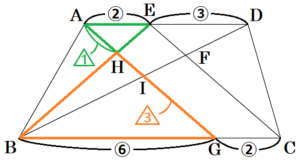
Ⅱ 図１において，四角形 \( ABCD \) は \( AD//BC \) の台形である。点 \( E \) は辺 \( AD \) 上の点であり，点 \( F \) は線分 \( BD \) と線分 \( CE \) の交点である。次の（１），（２）の問いに答えなさい。
（１） \( △FBC \) ∽ \( △FDE \) となることを証明しなさい。
\( △FBC \) と \( △FDE \) において，
\( AD//BC \) より，
錯角は等しいので，
\( ∠FBC=∠FDE \) ･･･ ➀
\( ∠FCB=∠FED \) ･･･ ➁
➀➁より，２組の角がそれぞれ等しいので，
\( △FBC \) ∽ \( △FDE \)
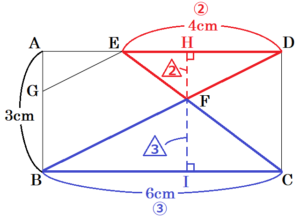
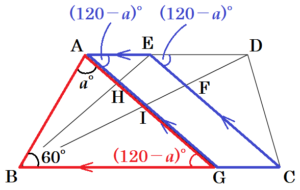
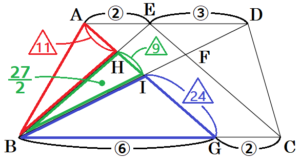
（２） 図２は，図１の辺 \( BC \) 上に点 \( G \) を \( AE=CG \) となるようにとり，線分 \( AG \) と線分 \( BE \) をかき加えたものである。点 \( H \) は線分 \( AG \) と線分 \( BE \) の交点であり，点 \( I \) は線分 \( AG \) と線分 \( BD \) の交点である。
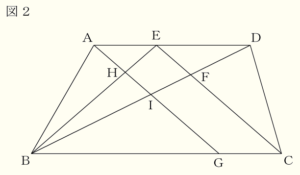
➀ \( ∠ABG=60°，∠BAH=a° \) のとき，\( ∠DEF \) の大きさを，\( a \) を用いて表しなさい。
\( △ABG \) において，
\( ∠AGB=180°-(∠ABG+∠BAH) \)
\( =180°-(60°+a°) \)
\( =(120-a)° \)
\( AD//BC \) より，錯角は等しいので，
\( ∠EAG=∠AGB=(120-a)° \)
\( AD//BC，AE=CG \) より，
四角形 \( AGCE \) は平行四辺形なので，
\( AG//EC \) であり，同位角は等しいので，
\( ∠DEF=∠EAG=(120-a)° \)
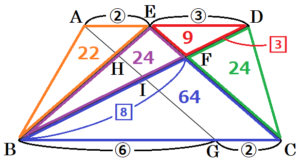
➁ \( AE：ED=2：3，BG：GC=3：1 \) のとき，四角形 \( EHIF \) の面積は，四角形 \( ABCD \) の面積の何倍か，求めなさい。
\( AE：ED=2：3，BG：GC=3：1，AE=CG \) より，
\( AE：ED：BG：GC=2：3：6：2 \)
【四角形 \( ABCD \) の面積は？】
\( △FDE \) ∽ \( △FBC \) なので，
\( ED：BC=3：8 \) より，面積比は，
\( △FDE：△FBC=3^2：8^2=9：64 \)
\( △FDE \) と \( △FBE \) は，高さが共通なので，
面積比は，
\( △FDE：△FBE=FD：FB=9：24 \)
同様に，
\( △FDE：△FDC=FE：FC=9：24 \)
\( △ABE \) と \( △DBE \) は，高さが共通なので，
面積比は，
\( △ABE：△DBE=AE：ED=22：33 \)
以上より，\( △FDE \) の面積を \( 9 \) とすると，
四角形 \( ABCD \) の面積は，\( 143 \) と表すことができます。･･･（ア）
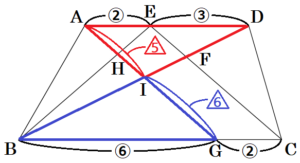
【\( AH：HI：GI \) を求める】
\( △IDA \) ∽ \( △IBG \) なので，
\( AI：GI=AD：GB=5：6 \)
\( △HEA \) ∽ \( △HBG \) なので，
\( AH：GH=AD：GB=1：3 \)
\( AI：GI=5：6=20：24 \)
\( AH：GH=1：3=11：33 \)
より，
\( AH：HI：GI=AH：(AI-AH)：GI \)
\( =11：(20-11)：24 \)
\( =11：9：24 \)
【四角形 \( EHIF \) の面積は？】
\( △ABG \) と \( △DBC \) は，高さが共通なので，
面積比は，
\( △ABG：△DBC=BG：GC=3：4 \)
\( △FDE \) の面積を \( 9 \) とすると，
\( △DBC \) の面積は，\( 64+24=88 \) と表せるので，
\( △ABG \) の面積は，\( 88 \times \dfrac{3}{4}=66 \)
このとき，\( △IBH \) の面積は，\( 66 \times \dfrac{9}{44}=\dfrac{27}{2} \) と表すことができます。
四角形 \( EHIF=△FBE-△IBH \) より，
四角形 \( EHIF \) の面積は，\( 24-\dfrac{27}{2}=\dfrac{21}{2} \) と表すことができます。 ･･･（イ）
結論
（ア）（イ）より，四角形 \( EHIF： \) 四角形 \( ABCD=\dfrac{21}{2}：143=21：286 \) となるので，
四角形 \( EHIF \) の面積は，四角形 \( ABCD \) の面積の \( \dfrac{21}{286} \) 倍になります。
