大問1
1 \( (-2) \times 5 \)
2 \( \dfrac{3}{4}-(-\dfrac{1}{5}) \)
【解答】
\( \dfrac{19}{20} \)
【解説】
\( =\dfrac{3}{4}+\dfrac{1}{5} \)
\( =\dfrac{15}{20}+\dfrac{4}{20} \)
\( =\dfrac{19}{20} \)
3 \( 20a^2b \div (-2a) \div (-b) \)
【解説】
\( =20a^2b \times \left( -\dfrac{1}{2a} \right) \times \left( -\dfrac{1}{b} \right) \)
\( =\dfrac{20a^2b}{2a \times b} \)
\( =10a \)
4 \( (2-\sqrt{3})(2+\sqrt{3})-\dfrac{\sqrt{27}}{\sqrt{3}} \)
【解説】
\( =(4-3)-\dfrac{3\sqrt{3}}{\sqrt{3}} \)
\( =1-3 \)
\( =-2 \)
5 \( (x+1)^2+(x-2)(x+3) \)
【解説】
\( =(x^2+2x+1)+(x^2+x-6) \)
\( =2x^2+3x-5 \)
大問2
1 二次方程式 \( (x-2)^2=5 \) を解け。
【解説】
\( (x-2)^2=5 \)
\( x-2=±\sqrt{5} \)
\( x=2±\sqrt{5} \)
2 次のア~エのうち,\( y \) が \( x \) に反比例するものを1つ選び,その記号を書け。
ア 長さ \( 100 \; cm \) のひもを,\( x \; cm \) 使ったときの残りの長さ \( y \; cm \)
イ 面積 \( 20 \; cm^2 \),縦の長さ \( x \; cm \) の長方形の横の長さ \( y \; cm \)
ウ 半径 \( x \; cm \) の円の面積 \( y \; cm^2 \)
エ 1個 \( 250 \) 円のお菓子を,\( x \) 個買ったときの代金 \( y \) 円
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \) (\( a \) は定数) になります。
ア~
エそれぞれついて,\( y \) を \( x \) の式で表すと,
ア ・・・ \( y=100-x \; (cm) \)
イ ・・・ \( y=\dfrac{20}{x} \; (cm) \)
ウ ・・・ \( y=\pi{}x^2 \; (cm^2) \)
エ ・・・ \( y=250x \) (円)
なので,あてはまるのは イ になります。
3 \( \sqrt{60}<n \) となる自然数 \( n \) のうち,最も小さいものを求めよ。
【解説】
\( \sqrt{\phantom{ }} \) を使って表された数が自然数になるのは,\( \sqrt{\phantom{ }} \) の中の数が整数の2乗で表せるときです。
\( \sqrt{60} \) に近い数で \( \sqrt{\phantom{ }} \) の中の数が整数の2乗になるのは
\( \sqrt{49}=\sqrt{7^2}=7 \)
\( \sqrt{64}=\sqrt{8^2}=8 \)
なので,
\( \sqrt{49}<\sqrt{60}<\sqrt{64}=8 \) より,
\( \sqrt{60}<n \) となる自然数 \( n \) のうち,最も小さいものは \( 8 \) になります。
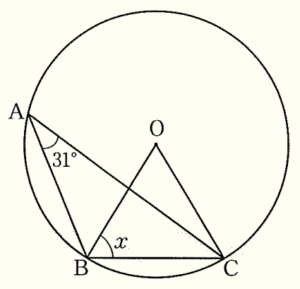
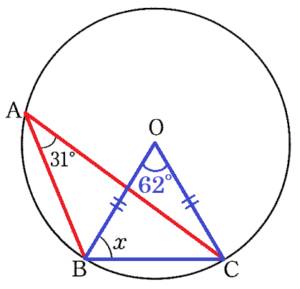
4 右の図で,3点 \( A,B,C \) は円 \( O \) の周上にあり,\( ∠BAC=31° \) である。このとき,\( ∠x \) の大きさを求めよ。
【解説】
\( ∠BAC \) は \( \stackrel{\huge\frown}{ BC } \) に対する円周角,
\( ∠BOC \) は \( \stackrel{\huge\frown}{ BC } \) に対する中心角,
なので,
\( ∠BOC=2∠BAC=62° \)
線分 \( OB,OC \) は,どちらも円 \( O \) の半径であり,
\( △OBC \) は \( OB=OC \) の二等辺三角形なので,
\( ∠x=\dfrac{180°-62°}{2}=59° \)
5 大小2つのさいころを同時に投げ, 大きい方のさいころの出る目の数を \( a \),小さい方のさいころの出る目の数を \( b \) とする。このとき,\( \dfrac{a}{b} \) の値が \( 1< \dfrac{a}{b} <2 \) になる確率を求めよ。ただし,さいころは,\( 1 \) から \( 6 \) までのどの目が出ることも同様に確からしいものとする。
【解説】
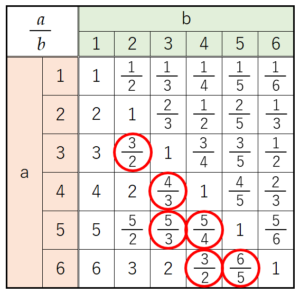
\( a,b \) の組み合わせとそれぞれの場合の \( \dfrac{a}{b} \) の値を表に書き出し,\( 1< \dfrac{a}{b} <2 \) になるところに ○ をつけると右のようになります。
\( 1< \dfrac{a}{b} <2 \) になる組み合わせは \( 6 \) 通り,
すべての組み合わせは \( 36 \) 通りなので,
求める確率は \( \dfrac{6}{36}=\dfrac{1}{6} \) になります。
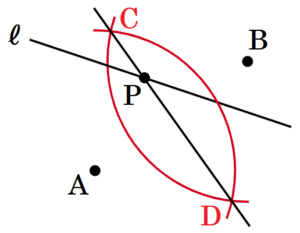
6 下の図のように,2点 \( A,B \) と直線 ℓ がある。2点 \( A,B \) から等しい距離にある直線 ℓ 上の点 \( P \) を,解答欄に作図せよ。ただし,作図に用いた線は消さずに残しておくこと。
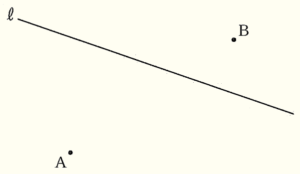
【解答】
手順1 2点 \( A,B \) を中心に円弧を描く
(交点を \( C,D \) とします)
手順2 2点 \( C,D \) を通る直線を描く
直線 ℓ と手順2の直線の交点が求める点 \( P \) になります。
【解説】
2点 \( A,B \) から等しい距離にある点は,必ず線分 \( AB \) の垂直二等分線上の点になります。
線分 \( AB \) の中点を \( M \),
2点 \( A,B \) から等しい距離にある点を \( P \)
とすると,
\( △APM \) と \( △BPM \) において,
仮定より,
\( AP=BP \) ・・・ ➀
\( AM=BM \) ・・・ ➁
\( △ABP \) は,二等辺三角形なので,
\( ∠PAM=∠PBM \) ・・・ ➂
➀➁➂より,
2組の辺とその間の角がそれぞれ等しいので,
\( △APM≡△BPM \)
合同な三角形の対応する角は等しいので,
\( ∠AMP=∠BMP=90° \)
よって,線分 \( PM \) は線分 \( AB \) の垂直二等分線になっています。
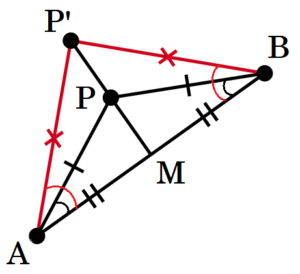
また,2点 \( A,B \) から等しい距離にある点のうち,点 \( P \) と異なる点を \( P’ \) とすると,
同様の考え方から,線分 \( P’M \) も線分 \( AB \) の垂直二等分線になっていることが証明できます。
よって,2点 \( A,B \) から等しい距離にある点は,必ず線分 \( AB \) の垂直二等分線上の点になります。
7 ある中学校では,毎年3月に,入学式の案内を,送付先に応じて,はがきか手紙のいずれかの方法で送付している。今年の3月も,昨年と同じ送付先に,昨年と同じ方法で送付しようとしたところ,昨年10月から,下の資料のように1通当たりの郵便料金が変更されたため,郵便料金の総額が,昨年送付するのにかかった郵便料金の総額と比べて,\( 4880 \) 円の増加になることが分かった。そこで,全てはがきによる送付に変えたところ,増加を \( 1880 \) 円に抑えることができた。 昨年送付したはがきと手紙は,それぞれ何通か求めよ。ただし,用いる文字が何を表すかを最初に書いてから連立方程式をつくり,答えを求める過程も書くこと。

【解答】
昨年送付したはがきを \( x \) 通,手紙を \( y \) 通とすると,
\( \left\{ \begin{array}{}
(85x+110y)-(63x+84y)=4880 \;\; ・・・ \;\; ➀ \\
85(x+y)-(63x+84y)=1880 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀を整理すると,
\( 22x+26y=4880 \) ・・・ ➀’
➁を整理すると,
\( 22x+y=1880 \) ・・・ ➁’
➀’\( – \)➁’すると,
\( 25y=3000 \)
\( y=120 \)
➁’に代入すると,
\( 22x+120=1880 \)
\( 22x=1760 \)
\( x=80 \)
よって,
昨年送付したはがきは \( 80 \) 通
昨年送付した手紙は \( 120 \) 通
大問3
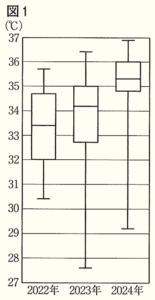
1 右の図1は,ある都市の, 2022年,2023年,2024年における,8月の日ごとの最高気温のデータを,年別に箱ひげ図に表したものである。
(1) 2024年8月の31日間において,最高気温が \( 35.0\;^\circ C \) 以上であった日が16日以上あるかどうかは,2024年8月の日ごとの最高気温の,次のア~エのいずれかの値に着目することで分かる。その値として適当なものを,ア~エから1つ選び,その記号を書け。
ア 最大値 イ 中央値 ウ 最小値 エ 平均値
【解説】
図1の箱ひげ図は31日分のデータからできているので,中央値になるのは気温の高い方から16番目の値になります。
2024年8月の箱ひげ図の中央値は \( 35.0\;^\circ C \) より大きい(高い)ので,
最高気温が \( 35.0\;^\circ C \) 以上であった日が16日以上あるといえます。
(2) 8月の日ごとの最高気温について,図1から読み取れることとして正しいものを,次のア~エから1つ選び,その記号を書け。
ア 2023年には,最高気温が \( 33.0\;^\circ C \) であった日がある。
イ 最高気温が \( 31.0\;^\circ C \) 以下であった日の数は,2024年より2023年の方が多い。
ウ 2022年,2023年,2024年のうち,四分位範囲が最も大きいのは,2022年である。
エ 2022年,2023年,2024年のいずれの年にも,最高気温が \( 36.0\;^\circ C \) 以上であった日がある。
【解説】
● 正しいといえる理由
ウ ・・・ 各年のおよその四分位範囲は次のとおりです
2022年:\( 34.7-32.0=2.7 \;(^\circ C) \)
2023年:\( 35.0-32.7=2.3 \;(^\circ C) \)
2024年:\( 36.0-34.8=1.2 \;(^\circ C) \)
よって,四分位範囲が最も大きいのは,2022年であるといえます。
● 必ず正しいとはといえない理由
ア ・・・ 図1の箱ひげ図は31日分のデータからできているので,
(およその)値が読み取れるのは,
最小値,第1四分位数,中央値,第3四分位数,最大値
いずれかの値だけです。
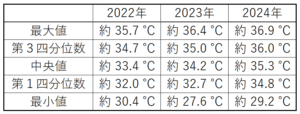
各年の箱ひげ図でこれらの値にあたるのは次の表のとおりで,\( 33.0\;^\circ C \) の日はありません。
つまり,最高気温が \( 33.0\;^\circ C \) であった日があるかどうかは箱ひげ図のデータからだけでは
わかりません。
イ ・・・ 2023年,2024年ともに,第1四分位数が \( 31.0\;^\circ C \) より大きい値であることから,
最高気温が \( 31.0\;^\circ C \) 以下であった日の数は,7日以下であることはわかります。
しかし,最高気温が低い方から2番目から7番目までの詳しい値は
箱ひげ図のデータからだけではわかりません。
よって,最高気温が \( 31.0\;^\circ C \) 以下であった日の数が,2024年より2023年の方が多いか
はわかりません。
エ ・・・ 2022年の最大値は \( 36.0\;^\circ C \) 未満なので,正しくありません。
(3) 図1の3つの箱ひげ図を比較すると,「8月の日ごとの最高気温は,2022年から2024年にかけて,高くなる傾向にある」と主張することができる。そのように主張することができる理由を,「第1四分位数」「第3四分位数」の2つの言葉を用いて,解答欄の書き出しに続けて簡単に書け。
【解答】
(2022年から2024年にかけて,)
第1四分位数と第3四分位数が大きくなっているから。
【解説】
箱ひげ図の箱の中には全体の約50%(半分)のデータが含まれます。
各年の箱ひげ図から,年ごとに箱の位置が上に移っていて,約半数の日の最高気温が
2022年:\( 32.0 \;^\circ C \) 以上 \( 34.7 \;^\circ C \) 以下
2023年:\( 32.7 \;^\circ C \) 以上 \( 35.0 \;^\circ C \) 以下
2024年:\( 34.8 \;^\circ C \) 以上 \( 36.0 \;^\circ C \) 以下
であったことがわかります。
つまり,箱の位置が上に移っているということは,気温が高くなる傾向にあるということになります。
「箱の位置が上に移っている」ことを,「第1四分位数」「第3四分位数」の2つの言葉を用いてあらわすと,
「(2022年から2024年にかけて,)第1四分位数と第3四分位数が大きくなっている」
になります。
2 下の表と図2は,ある都市の,2024年における,8月1日~9月2日の日ごとの最高気温のデータを,8月1日~8月31日,8月2日~9月1日,8月3日~9月2日の期間別に,まとめたものと箱ひげ図に表したものである。8月1日,8月2日,9月1日,9月2日の最高気温が,全て異なり,次のア~オのいずれかであることが分かっているとき,9月1日,9月2日の最高気温として適当なものを,ア~オからそれぞれ1つずつ選び,その記号を書け。
ア \( 32.6 \) イ \( 35.2 \) ウ \( 35.5 \) エ \( 36.2 \) オ \( 36.9 \)

【解答】
9月1日 ・・・ エ \( 36.2 \)
9月2日 ・・・ ア \( 32.6 \)
【解説】
3つの箱ひげ図に含まれるデータにどのような違いがあるかを考えると,
「8月2日~9月1日」の箱ひげ図に含まれるデータは,
「8月1日~8月31日」の箱ひげ図に含まれるデータから
8月1日のデータを削除し,9月1日のデータを追加したものになっています。
「8月3日~9月2日」の箱ひげ図に含まれるデータは,
「8月2日~9月1日」の箱ひげ図に含まれるデータから
8月2日のデータを削除し,9月2日のデータを追加したものになっています。

【オ \( 36.9 \;^\circ C \) にあたるのは何日?】
表から,最大値に注目すると,オ \( 36.9 \;^\circ C \) の日は,8月1日~8月31日と8月2日~9月1日の期間には含まれているが,8月3日~9月2日の期間には含まれていない日であるとわかります。
これは8月2日なので,オ \( 36.9 \;^\circ C \) は,8月2日の最高気温になります。
データを削除・追加した場合の並び順の変化について例を使って考えてみる
他の日の最高気温を見つけるにあたり,箱ひげ図に含まれるデータからあるデータを削除し,
別のデータを追加した場合に中に含まれるデータの並び順がどのように変わるかを
例を使って考えてみます。
ある箱ひげ図に含まれる15個のデータを小さい方から順に並べ,
A~Oの名前をつけて考えることにします。
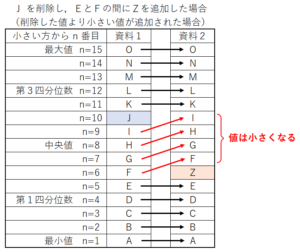
● F を削除し,JとKの間にZを追加すると・・・
削除したところより小さい値(\( n=1 \) から \( n=5 \)),
追加したところより小さい値(\( n=11 \) から \( n=15 \))
については値は変わりません。
削除したところから追加したところまでの間の値(\( n=6 \) から \( n=9 \))
についてはもとの値より大きい値になります。
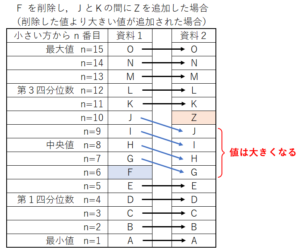
● J を削除し,EとFの間にZを追加すると・・・
追加したところより小さい値(\( n=1 \) から \( n=5 \)),
削除したところより小さい値(\( n=11 \) から \( n=15 \))
については値は変わりません。
削除したところから追加したところまでの間の値(\( n=6 \) から \( n=9 \))
についてはもとの値より大きい値になります。
この例の考え方を参考に,8月3日,9月1日,9月2日の最高気温について考えていきます。
【9月1日の最高気温は?】
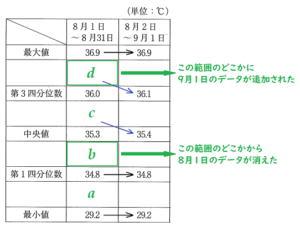
表の「8月1日~8月31日」と「8月2日~9月1日」の範囲における代表値の変化に注目すると,
中央値と第三四分位数だけが「8月2日~9月1日」の方が大きい値になっています。
ここから,追加された9月1日のデータは第三四分位数( \( 36.0 \;^\circ C \) )より大きく,
最大値( \( 36.9 \;^\circ C \) )より小さい値であったことがわかります。
よって,あてはまるのは エ \( 36.2 \;^\circ C \) になります。
ちなみに,消えた8月1日のデータは第一四分位数( \( 34.8 \;^\circ C \) )より大きく,
中央値( \( 35.3 \;^\circ C \) )より小さい値であったことがわかり,
あてはまるのは イ \( 35.2 \;^\circ C \) になります。
【9月2日の最高気温は?】
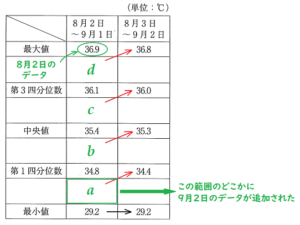
表の「8月2日~9月1日」と「8月3日~9月2日」の範囲における代表値の変化に注目すると,
第一四分位数,中央値,第三四分位数と最大値が「8月3日~9月2日」の方が小さい値になっています。
ここから,追加された9月2日のデータは最小値( \( 29.2 \;^\circ C \) )より大きく,
第一四分位数( \( 34.8 \;^\circ C \) )より小さい値であったことがわかります。
よって,あてはまるのは ア \( 32.6 \;^\circ C \) になります。
大問4
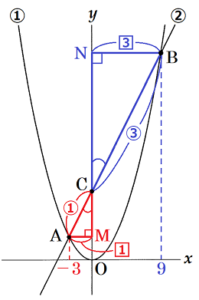
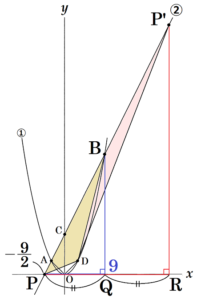
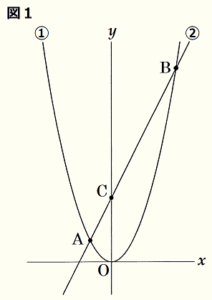
下の図1において,放物線①は関数 \( y=ax^2 \) のグラフであり,直線②は①上の2点 \( A,B \) を通る。点 \( A \) の座標は \( (-3,3) \),点 \( B \) の \( x \) 座標は正であり,直線②と \( y \) 軸との交点を \( C \) とすると,\( AC:CB=1:3 \) である。
このとき,次の問いに答えなさい。
1 \( a \) の値を求めよ。
【解答】
\( a=\dfrac{1}{3} \)
【解説】
関数 \( y=ax^2 \) のグラフは,\( A(-3,3) \) を通るので,
\( 3=a \times (-3)^2 \)
\( 9a=3 \)
\( a=\dfrac{1}{3} \)
2 点 \( B \) の \( x \) 座標を求めよ。
【解説】
2点 \( A,B \) から \( y \) 軸に垂線をひいた交点を
\( M,N \) とすると,
\( △ACM \) ∽ \( △BCN \) なので,
対応する辺の比は等しく,
\( AM:BN=AC:CB=1:3 \)
\( AM=3 \) なので,
\( AM:BN=1:3 \)
\( 3:BN=1:3 \)
\( BN=9 \)
よって,点 \( B \) の \( x \) 座標は \( 9 \) になります。
3 直線②の式を求めよ。
【解説】
点 \( B \) は \( y=\dfrac{1}{3}x^2 \) 上の点で,\( x \) 座標は \( 9 \) なので,
\( y \) 座標は
\( y=\dfrac{1}{3} \times 9^2=27 \)
直線②は,\( A(-3,3),B(9,27) \) を通るので,
直線②の式を \( y=cx+d \) とすると,
傾き \( c=\dfrac{27-3}{9-(-3)}=2 \)
\( y=2x+d \) に \( x=9,y=27 \) を代入すると,
\( 27=2 \times 9+d \)
\( d=9 \)
よって,直線②の式は \( y=2x+9 \) になります。
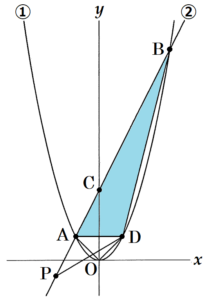
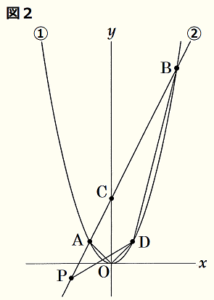
4 右の図2のように, 放物線①上の \( x \) 座標が \( 3 \) である点を \( D \) とする。また,点 \( P \) は直線②上を動く点とする。点 \( P \) の \( x \) 座標を \( t \) とするとき,四角形 \( OABD \) の面積と \( △PBD \) の面積が等しくなるのは,\( t= \) ア のときと,\( t= \) イ のときである。 ア , イ に当てはまる数を,それぞれ書け。
【解答】
ア ・・・ \( -\dfrac{9}{2} \)
イ ・・・ \( \dfrac{45}{2} \)
【解説】
【\( P \) が点 \( B \) より下側にあるとき】
補助線 \( AD \) をひくと,
四角形 \( OABD=△ABD+△AOD \)
\( △PBD=△ABD+△APD \)
なので,四角形 \( OABD \) の面積と \( △PBD \) の面積が等しくなるとき,
\( △AOD=△APD \)
になります。
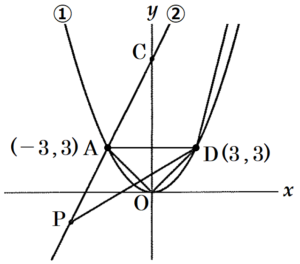
点 \( D \) は,放物線①上の点で,\( x \) 座標が \( 3 \) なので,
\( y \) 座標は
\( y=\dfrac{1}{3} \times 3^2=3 \)
であり,線分 \( AD \) は \( x \) 軸と平行になっています。
\( △AOD \) と \( △APD \) は線分 \( AD \) が共通で,
原点 \( O \) は \( x \) 軸上の点なので,
等積変形の考え方から,
\( △AOD=△APD \) となるのは,
点 \( P \) が \( x \) 軸上にあるときです。
点 \( P \) の座標を \( P(t,0) \) とすると,
点 \( P \) は,直線②上の点で,\( y \) 座標が \( 0 \) なので,
\( 0=2t+9 \)
\( t=-\dfrac{9}{2} \)
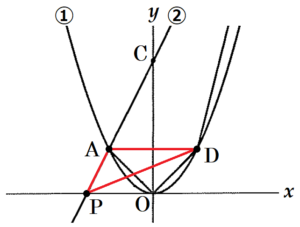
【\( P \) が点 \( B \) より上側にあるとき】
\( P \) が点 \( B \) より上側にある場合を \( P’ \) とすると,
\( △PBD \) と \( △P’BD \) は,3点 \( B,P,P’ \) が
直線②上にあり,高さが共通なので,
\( PB=P’B \) となるとき,
\( △PBD=△P’BD \) となります。
点 \( B,P’ \) から \( x \) 軸に垂線をひき,
交点を \( Q,R \) とすると,
\( △PBQ \) ∽ \( △PP’R \) であり,
対応する辺の比は等しいので,
\( PB=P’B \) のとき,\( PQ=QR \) となります。
点 \( B \) と点 \( Q \) の \( x \) 座標は \( 9 \) なので,
\( PQ=9-\left( -\dfrac{9}{2} \right)=\dfrac{27}{2} \)
点 \( P’ \) と点 \( R \) の \( x \) 座標が \( t \) のとき,
\( PQ=QR \)
\( \dfrac{27}{2}=t-9 \)
\( t=\dfrac{45}{2} \)
大問5
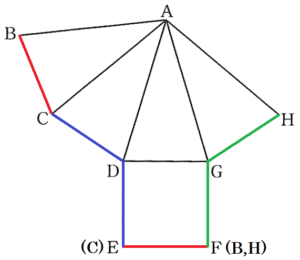
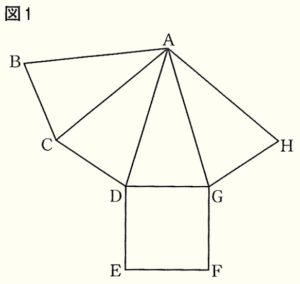
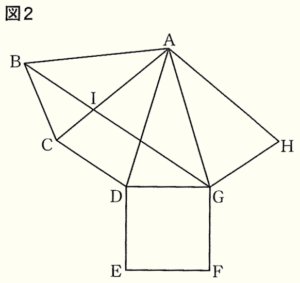
1 下の図1は,正四角すいの展開図である。
(1) 図1を組み立ててできる正四角すいにおいて,点 \( B \) と重なる点を,図1の7つの点 \( A,C,D,E,F,G,H \) の中から全て選び,\( A,C,D,E,F,G,H \) の記号で書け。
【解説】
この正四角すいを組み立てると,
辺 \( BC \) と辺 \( FE \)
辺 \( CD \) と辺 \( ED \)
辺 \( GH \) と辺 \( GF \)
が重なるので,点 \( B \) と重なる点は。
\( F \) と \( H \) になります。
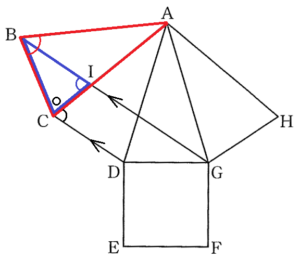
(2) 下の図2は,図1において点 \( B \) と点 \( G \) を結んだ図であり,\( BG//CD \) である。また,線分 \( BG \) と線分 \( AC \) との交点を \( I \) とする。このとき,\( △ABC \) ∽ \( △BIC \) であることを証明せよ。
【解答】
\( △ABC \) と \( △BIC \) において,
共通な角なので,
\( ∠ACB=∠BCI \) ・・・ ➀
\( BG//CD \) より,錯角は等しいので,
\( ∠BIC=∠ACD \) ・・・ ➁
正四角すいの側面は合同な三角形なので,
\( △ABC≡△ACD \) であり,
対応する角は等しいので,
\( ∠ABC=∠ACD \) ・・・ ➂
➁➂より,
\( ∠ABC=∠BIC \) ・・・ ➃
➀➃より,2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △BIC \)
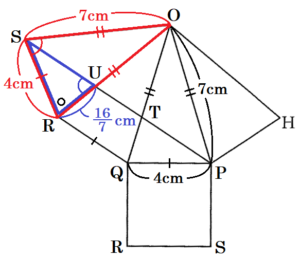
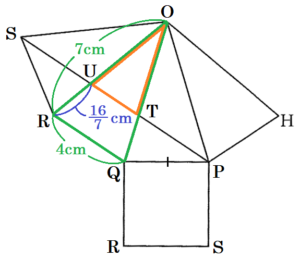
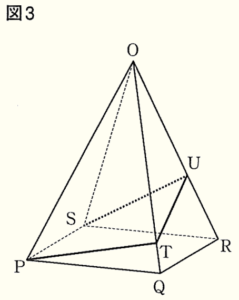
2 下の図3のように,\( OP=7 \; cm,PQ=4 \; cm \) の正四角すい \( OPQRS \) があり,点 \( T,U \) は,それぞれ辺 \( OQ,OR \) 上を動く点である。3つの線分 \( PT,TU,US \) の長さの和 \( PT+TU+US \) が最小となるとき,線分 \( TU \) の長さを求めよ。
【解答】
\( \dfrac{132}{49} \; cm \)
【解説】
正四角すい \( OPQRS \) の展開図において,
\( PT+TU+US \) が最小となるとき,
4点 \( P,T,U,S \) は一直線上に並びます。
これは,図2と同じになっています。
(2)より \( △OSR \) ∽ \( △SUR \) なので,
\( OS=OP=7 \; cm,RS=PQ=4 \; cm \) であることから,
\( RS:RU=OS:SR \)
\( 4:RU=7:4 \)
\( RU=\dfrac{16}{7} \; (cm) \)
次に,\( △OTU \) と \( △OQR \) に注目すると,
(2)より \( SP//RQ \) なので,
\( △OTU \) ∽ \( △OQR \) になっています。
\( OR=OS=7 \; cm,RU=\dfrac{16}{7} \; cm \) より,
\( OU=7-\dfrac{16}{7}=\dfrac{33}{7} \; (cm) \)
対応する辺の比は等しいので,
\( TU:QR=OU:OR \)
\( TU:4=\dfrac{33}{7}:7 \)
\( TU=\dfrac{132}{49} \; (cm) \)




-300x246.png)