大問１
(1) 次の計算をせよ。
ア \( -3+(-2) \times (-5) \)
イ \( 4ac \times 6ab \div 3bc \)
ウ \( \sqrt{2} \times \sqrt{6}+ \sqrt{27} \)
エ \( \dfrac{a+2b}{2}-\dfrac{b}{3} \)
(2) \( a^2-a-6 \) を因数分解せよ。
(3) 次の連立方程式，二次方程式を解け。
ア \( \left\{ \begin{array}{} x-y=5 \\
2x+3y=-5 \end{array} \right. \)
イ \( x^2+x-1=0 \)
(4) 次の数量の関係を，不等式で表せ。
「１本５０円の鉛筆 \( x \) 本と１冊１００円のノート \( y \) 冊を買おうとしたが，１０００円ではたりなかった。」
(5) ３辺の長さが \( 2 \; cm，3 \; cm， \sqrt{13} \; cm \) である三角形が直角三角形になる理由を，言葉や数，式を用いて説明せよ。
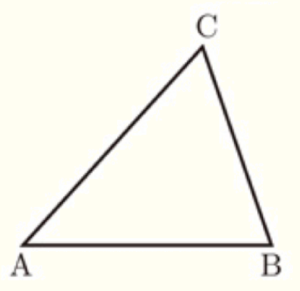
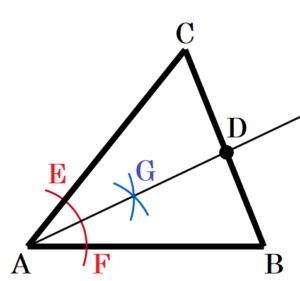
(6) 右の図で，\( △ABC \) の \( ∠A \) の二等分線と辺 \( BC \) の交点 \( D \) を作図せよ。ただし，作図に用いた線は消さないこと。
（交点を \( E，F \) とします）
手順２ 点 \( E，F \) を中心に同じ半径の弧を描く。
（交点を \( G \) とします）
手順３ 点 \( A，G \) を通る直線を描く。
手順３の直線と辺 \( BC \) の交点が \( D \) になります。
大問２
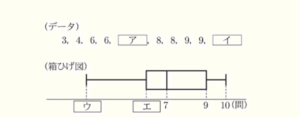
(1) ある学校の生徒１０人に対してクイズを１０問ずつ行った。それぞれの生徒の正解数を小さいほうから順に並べたデータと，そのデータの箱ひげ図は次のようになった。このとき， ア ～ エ にあてはまる値と，この１０人の正解数の四分位範囲を求めよ。
(2) 下の【証明】は \( △ABC \) の内角の和が \( 180° \) になることを証明したものである。
このとき， ア ， イ にあてはまる角を書き入れて証明を完成させよ。
【証明】
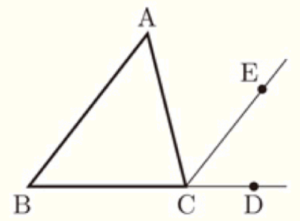
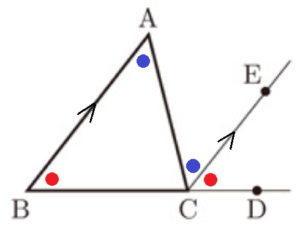
右の図のように，３点 \( B，C，D \) が一直線上にあるように
点 \( D \) をとり， \( AB//EC \) となるように点 \( E \) をとる。
平行線の同位角は等しいので，\( AB//EC \) から，
\( ∠ABC= \) ア ･･･ ①
また，平行線の錯角は等しいので，\( AB//EC \) から，
\( ∠BAC= \) イ ･･･ ②
①，②から，\( △ABC \) の内角の和を求めると，
\( ∠ABC+∠BAC+∠ACB \)
\( = \) ア \( + \) イ \( +∠ACB \)
\( =∠BCD \)
となり，３点 \( B，C，D \) は一直線上にあるから，
\( ∠BCD=180° \) であり，
\( △ABC \) の内角の和は \( 180° \) である。
ア ･･･ \( ∠ECD \)
イ ･･･ \( ∠ACE \)
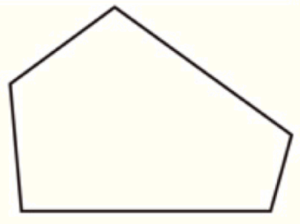
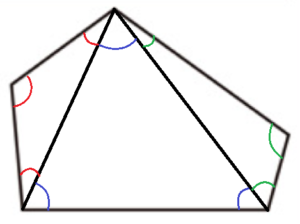
(3) 次の五角形の内角の和を求めよ。
三角形の内角の和は \( 180° \) なので，
五角形の内角の和は \( 180° \times 3=540° \)
大問３
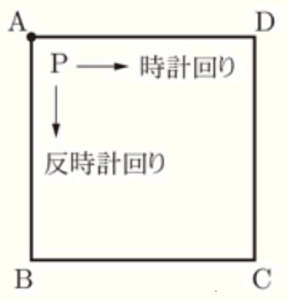
右の図は，１辺の長さが \( 1cm \) の正方形 \( ABCD \) である。点 \( P \) は最初，頂点 \( A \) にあり，１枚の硬貨を１回投げるごとに，正方形の辺上を，次の【規則】にしたがって動く。
【規則】
○ １回目に硬貨を投げるとき
・ 出た面が表のときは反時計回りに \( 1cm \)，
裏のときは時計回りに \( 2cm \) 動く。
○ ２回目，３回目に硬貨を投げるとき
・ 直前に投げた硬貨と同じ面が出た場合は，動かない。
・ 直前に投げた硬貨と違う面が出た場合は，
出た面が表のときは反時計回りに \( 1cm \)，
裏のときは時計回りに \( 2cm \) 動く。
(例) 硬貨を３回投げ，表，表，裏の順に出たとき，
点 \( P \) は頂点 \( D \) にある。
このとき，次の問いに答えよ。
ただし，硬貨の表と裏の出かたは同様に確からしいとする。
(1) 硬貨を２回投げるとき，点 \( P \) が頂点 \( C \) にある確率を求めよ。
硬貨を２回投げるとき，すべての場合の数は４通り。
そのうち，頂点 \( C \) になるのは，裏・裏のときの１通り。
よって，求める確率は \( \dfrac{1}{4} \)
(2) 硬貨を３回投げるとき，点 \( P \) がどの頂点にある確率がもっとも大きくなるか，
その頂点を書き，そのときの確率を求めよ。
硬貨を３回投げるとき，すべての場合の数は８通り。
そのうち，頂点 \( D \) になるのが，４通りで最も多くなります。
よって，求める確率は \( \dfrac{4}{8}=\dfrac{1}{2} \)
大問４
大きさが等しい正方形の白いタイル (□) と黒いタイル (■) がある。下の図のように，はじめに黒いタイルを１枚置き，その黒いタイルを囲むように，四隅は黒いタイルを，他の部分は白いタイルをすきまなく並べる。そのときできた正方形を１番目の図形とする。次に１番目の図形を囲むように，四隅は黒いタイルを，他の部分は白いタイルをすきまなく並べる。そのときできた正方形を２番目の図形とする。同様に，できた図形を囲むように，四隅は黒いタイルを，他の部分は白いタイルをすきまなく並べ，順に図形を作っていく。
このとき，次の問いに答えよ。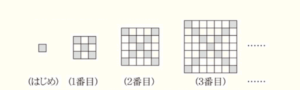
(1) ５番目の図形において，黒いタイルの枚数を求めよ。
(2) \( n \) 番目の図形において，黒いタイルの枚数と，すべてのタイルの枚数を，\( n \) を用いた式で表せ。
(3) 何番目の図形であっても，白いタイルの枚数は偶数の２乗になることを，言葉や数，式を用いて説明せよ。
大問５
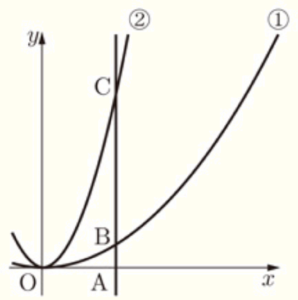
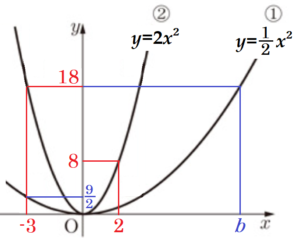
右の図のように，関数 \( y=\dfrac{1}{2}x^2 \) ･･･ ①，
関数 \( y=ax^2 \) ( \( a \) は正の定数) ･･･ ② のグラフがある。
\( x \) 軸上に点 \( A \) をとる。点 \( A \) から \( y \) 軸と平行な直線をひき，① のグラフとの交点を \( B \)，② のグラフとの交点を \( C \) とする。ただし，点 \( A \) の \( x \) 座標は正とする。
このとき，次の問いに答えよ。
(1) 点 \( C \) の \( y \) 座標が，点 \( B \) の \( y \) 座標よりも大きいとき，\( a \) の値と，\( \dfrac{1}{2} \) の関係について，
次のア～ウから正しいものを1つ選び，その記号を書け。
ア \( a<\dfrac{1}{2} \) イ \( a>\dfrac{1}{2} \) ウ \( a=\dfrac{1}{2} \)
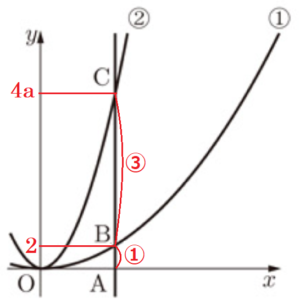
(2) 点 \( A \) の \( x \) 座標が \( 2 \) のとき，\( AB：BC = 1：3 \) であった。
ア ２点 \( B，C \) の \( y \) 座標と，\( a \) の値を求めよ。
\( x=2 \) のとき，
\( B \) の \( y \) 座標は，\( y=\dfrac{1}{2} \times 2^2=2 \)
\( C \) の \( y \) 座標は，\( y=a \times 2^2=4a \)
なので，
\( AB=2 \)，\( BC=4a-2 \) と表すことができます。
よって，
\( AB：BC=1：3 \)
\( 2：(4a-2)=1：3 \)
\( 4a-2=6 \)
\( a=2 \)
\( a=2 \) のとき，\( C \) の \( y \) 座標は，\( y=4 \times 2=8 \)
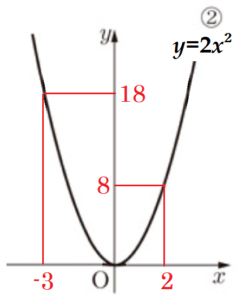
イ ②の関数について，\( x \) の変域が \( -3≦x≦2 \) のときの \( y \) の変域を求めよ。
\( y=ax^2 \) ( \( a>0 \) ) において，\( x \) の変域が \( 0 \) を含む場合，
\( y \) の変域の最小値は \( 0 \) になります。
また，\( y \) の変域が最大値をとるのは，
\( x \) の絶対値が最大になるときです。
\( -3≦x≦2 \) のとき，\( x \) の絶対値が最大になるのは
\( x=-3 \) のときなので，
②の関数 \( y=2x^2 \) において，
\( x=-3 \) のときの \( y \) 座標の値は，
\( y=2 \times (-3)^2=18 \)
よって，\( y \) の変域は，\( 0≦y≦18 \)
ウ ①の関数の \( x \) の変域が \( -3≦x≦b \) のときの \( y \) の変域と，イで求めた \( y \) の変域が等しくなった。
このとき，\( b \) の値を求めよ。
イの結果より，①の関数 \( y=\dfrac{1}{2}x^2 \) の \( y \) の変域が
\( 0≦y≦18 \) になるということです。
\( y=18 \) になるときの \( x \) の値は，
\( \dfrac{1}{2}x^2=18 \)
\( x^2=36 \)
\( x=±6 \)
\( x \) の変域は \( -3≦x≦b \) なので，
あてはまるのは，\( x=6 \) のみ。
よって， \( b=6 \)
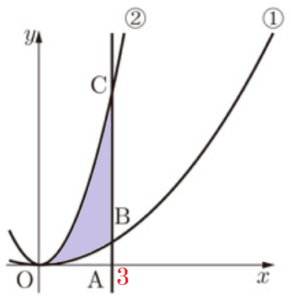
(3) \( a=3 \) ，点 \( A \) の \( x \) 座標が \( 3 \) のとき，①，②のグラフと線分 \( BC \) で囲まれた図形の周および内部において，\( x \) 座標，\( y \) 座標がともに整数である点の個数を求めよ。
\( x=0，1，2，3 \) のそれぞれについて，
\( y \) 座標の値の取り得る範囲を求め，
その中に，整数になる値がいくつあるかを数えていきます。
● \( x=0 \) のとき
➀の関数 ･･･ \( y=\dfrac{1}{2} \times 0^2=0 \)
➁の関数 ･･･ \( y=3 \times 0^2=0 \)
なので，取り得る \( y \) 座標の値は \( 0 \) のみ
よって，あてはまるのは１個
● \( x=1 \) のとき
➀の関数 ･･･ \( y=\dfrac{1}{2} \times 1^2=\dfrac{1}{2} \)
➁の関数 ･･･ \( y=3 \times 1^2=3 \)
なので，取り得る \( y \) 座標の範囲は
\( \dfrac{1}{2}≦y≦3 \)
よって，この範囲にある整数は３個
● \( x=2 \) のとき
➀の関数 ･･･ \( y=\dfrac{1}{2} \times 2^2=2 \)
➁の関数 ･･･ \( y=3 \times 2^2=12 \)
なので，取り得る \( y \) 座標の範囲は
\( 2≦y≦12 \)
よって，この範囲にある整数は１１個
● \( x=3 \) のとき
➀の関数 ･･･ \( y=\dfrac{1}{2} \times 3^2=\dfrac{9}{2} \)
➁の関数 ･･･ \( y=3 \times 3^2=27 \)
なので，取り得る \( y \) 座標の範囲は
\( \dfrac{9}{2}≦y≦27 \)
よって，この範囲にある整数は２３個
以上より，あてはまる点の個数は，
\( 1+3+11+23=38 \) （個）
