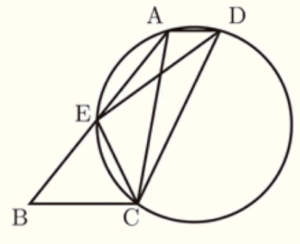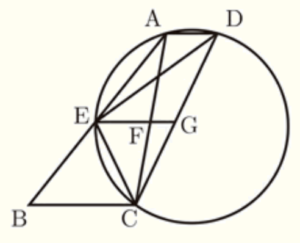大問1
(1) 次の計算をせよ。
ア \( 8-(-3) \times (-6) \)
【解説】
\( =8-18 \)
\( =-10 \)
イ \( \dfrac{a^2b}{12} \div \dfrac{ab}{3} \times \dfrac{a}{2} \)
【解答】
\( \dfrac{a^2}{8} \)
【解説】
\( =\dfrac{a^2b}{12} \times \dfrac{3}{ab} \times \dfrac{a}{2} \)
\( =\dfrac{a^2b \times 3 \times a}{12 \times ab \times 2} \)
\( =\dfrac{a^2}{8} \)
ウ \( \sqrt{28}-\dfrac{21}{\sqrt{7}} \)
【解説】
\( =2\sqrt{7}-\dfrac{21 \times \sqrt{7}}{\sqrt{7} \times \sqrt{7}} \)
\( =2\sqrt{7}-3\sqrt{7} \)
\( =-\sqrt{7} \)
(2) \( (a-b)x+(a-b)y \) を因数分解せよ。
(3) 次の連立方程式 \( \left\{ \begin{array}{}
x+2y=-2 \\
2x-y=11 \\
\end{array} \right. \) を解け。
【解説】
\( \left\{ \begin{array}{}
x+2y=-2 \;\; ・・・ \;\; ➀ \\
2x-y=11 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 2 \) すると,
\( 2x+4y=-4 \) ・・・ ➀’
➀’\( – \) ➁ すると,
\( 5y=-15 \)
\( y=-3 \)
➀に代入すると,
\( x+2 \times (-3)=-2 \)
\( x-6=-2 \)
\( x=4 \)
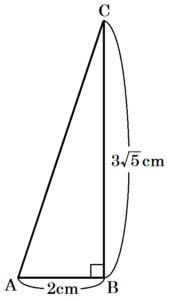
(4) \( △ABC \) について,\( AB=2 \; cm,BC=3\sqrt{5} \; cm,∠ABC=90° \) のとき,\( CA \) の長さを求めよ。
【解説】
\( AB=2 \; cm,BC=3\sqrt{5} \; cm,∠ABC=90° \) の直角三角形を図に書いてみると右の図のようになります。
三平方の定理より,
\( CA^2=2^2+(3\sqrt{5})^2=49 \)
\( CA=7 \; (cm) \) (\( CA>0 \) より)
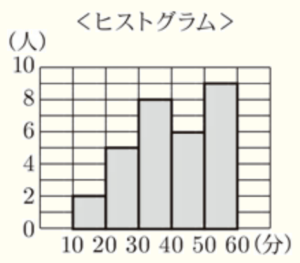
(5) あるクラスの生徒 \( 30 \) 人の登校に要する時間を調べたところ,ヒストグラムと箱ひげ図は右と下のようになった。このヒストグラムと箱ひげ図から最頻値と範囲をそれぞれ求めよ。
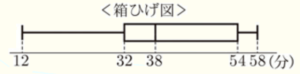
【解答】
【最頻値】 ・・・ \( 55 \)(分)
【範囲】 ・・・ \( 46 \)(分)
【解説】
【最頻値】
最頻値とは,度数が最も大きい階級の階級値のことです。
ヒストグラムから,度数が最も大きい階級は \( 50 \) 分以上 \( 60 \) 分未満の階級なので,
階級値は \( \dfrac{50+60}{2}=55 \)(分)
【範囲】
範囲は,「最大値 \( – \) 最小値」で求めることができます。
箱ひげ図から,最大値は \( 58 \) 分,最小値は \( 12 \) 分なので,
範囲は \( 58-12=46 \)(分)
(6) 『連続する3つの偶数の2乗の和に を加えた数は12の倍数になる。』 ということがらが正しくなるように, にあてはまる数を1つみつけよ。また,そのことがらが正しいことを言葉や数,式などを用いて説明せよ。
【解答】
\( 4 \)
\( n \) を整数とすると,連続する3つの偶数は \( 2n-2,2n,2n+2 \) と表すことができる。
また,,
にあてはまる数を \( 4 \) とすると,
連続する3つの偶数の2乗の和に \( 4 \) を加えた数は
\( (2n-2)^2+(2n)^2+(2n+2)^2+4 \)
\( =(4n^2-8n+4)+4n^2+(4n^2+8n+4)+4 \)
\( =12n^2+12 \)
\( =12(n^2+1) \)
となり,\( n \) が整数であるとき,\( n^2+1 \) も整数なので,
\( 12(n^2+1) \) は12の倍数である。
よって,連続する3つの偶数の2乗の和に \( 4 \) を加えた数は12の倍数になる。
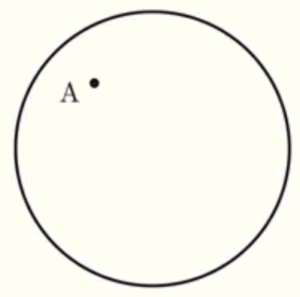
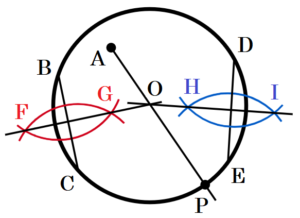
(7) 右の図のように, 円とその内部に点 \( A \) がある。この円周上に \( AP \) の長さが最大となるような点 \( P \) を作図せよ。
ただし, 作図に用いた線は消さないこと。
【解答】
手順1 問題の円に対し,2本の弦を描く。
(弦 \( BC \),弦 \( DE \) とします。)
手順2 2点 \( B,C \) を中心に,円弧を描く。
(交点を点 \( F,G \) とします。)
手順3 2点 \( F,G \) をを通る直線を描く。
手順4 2点 \( D,E \) を中心に,円弧を描く。
(交点を点 \( H,I \) とします。)
手順5 2点 \( H,I \) を通る直線を描く。
(手順3と手順5の直線の交点を点 \( O \) とします)
手順6 2点 \( A,O \) を通る直線を描く。
このとき,手順6の直線と円の交点のうち,\( A \) から遠い方の点が求める点 \( P \) になります。
【解説】
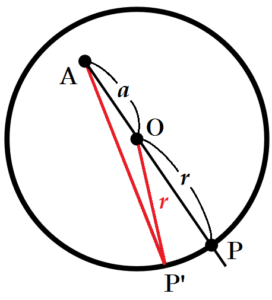
半径が \( r \) の円 \( O \) において,
円周上に3点 \( A,O,P \) が一直線に並ぶような
点を \( P \),\( AO=a \) とするとき,
\( AP \) の長さは,\( a+r \) となります。
また,円周上の \( P \) と異なる点を \( P’ \) とするとき,
円 \( O \) の中に \( △AOP’ \) ができます。
このとき,\( AO=a,OP’=r \) であることから,
\( AP \) の長さは,2辺の長さの和 \( a+r \) より
短くなります。
よって,\( AP \) の長さが最大となるのは,3点 \( A,O,P \) が一直線に並ぶときになります。
【参考】
すべての三角形において,1辺の長さは,残りの2辺の長さの和より短くなります。
大問2
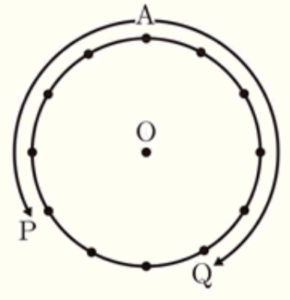
右の図のように,周の長さが \( 12 \; cm \) である円 \( O \) と,\( 1,2,3,4,5,6 \) のカードが1枚ずつ入っている箱がある。また,円 \( O \) の円周を12等分する点があり,点 \( A \) はそのうちの1つである。2点 \( P,Q \) は,はじめに点 \( A \) の位置にあり,次の【手順】にしたがって円周上を移動する。
【手順】
[1] 箱から1枚カードを取り出し,そのカード
に書かれた数を \( x \) として,点 \( P \) を
反時計回りに \( x \; cm \) 動かす。
[2] [1]で取り出したカードを元に戻さず,
箱からもう1枚カードを取り出し,その
カードに書かれた数を \( y \) として,点 \( Q \)
を時計回りに \( y \; cm \) 動かす。
ただし,箱からのカードの取り出し方は同様に確からしいとする。このとき,次の問いに答えよ。
(1) \( x=4,y=5 \) となる確率を求めよ。また,そのときの \( ∠PAQ \) の大きさを求めよ。
【解答】
確率 ・・・ \( \dfrac{1}{30} \)
\( ∠PAQ=45° \)
【解説】
【\( x=4,y=5 \) となる確率】
選んだカードの組み合わせを樹形図に書き出すと,\( x=4,y=5 \) になる組み合わせは1通り,
全ての組み合わせは30通りなので,求める確率は \( \dfrac{1}{30} \)

【\( ∠PAQ \) の大きさ】
円周上の点は12等分しているので,
点1個分のおうぎ形の中心角は \( \dfrac{360}{12}=30° \) です。
\( x=4,y=5 \) のとき,おうぎ形\( POQ \) は,
点3個分の大きさなので,
\( ∠POQ=30° \times 3=90° \)
\( ∠POQ \) は \( \stackrel{\huge\frown}{ PQ } \) に対する中心角,
\( ∠PAQ \) は,\( \stackrel{\huge\frown}{ PQ } \) に対する円周角なので,
\( ∠PAQ=90° \times \dfrac{1}{2}=45° \)
\( \phantom{ } \)
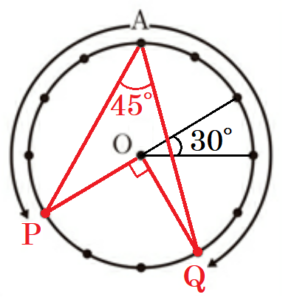
(2) \( ∠PAQ=60° \) となる確率を求めよ。
【解説】
12個の点にそれぞれ \( A~L \) の名前をつけます。
このとき,点 \( P \) が動く範囲は \( G~L \),点 \( Q \) が動く範囲は \( B~G \) になります。
\( ∠PAQ=60° \) になるとき,\( ∠POQ=120° \) になるので,おうぎ形 \( POQ \) が点4個分の大きさになります。
ここから,\( x=1~6 \) それぞれの場合において,点 \( Q \) がどの点に移動すれば \( ∠POQ=120° \) になるかを考えていきます。
ただし,以下の点に注意が必要です。
注1 ・・・ 手順[1]で選んだカードは戻さないので,\( (x,y)=(1,1),(2,2) \) など
\( x \) と \( y \) の値が同じになることはありません。
注2 ・・・ 点 \( A \) が \( \stackrel{\huge\frown}{ PQ } \) 上(短い方)にあるときはあてはまりません。
(\( ∠PAQ=120° \) になるため)
【 点 \( P \) が点 \( L \) に移動する(\( x=1 \))場合】
点 \( P \) が点 \( L \) に移動するとき,
\( ∠POQ=120° \) になるのは,
点 \( Q \) が点 \( D \) または \( H \) に移動するときです。
ただし,点 \( A \) が \( \stackrel{\huge\frown}{ PQ } \) 上(短い方)にあるので,
\( (x,y)=(1,3) \) のときには \( ∠PAQ=60° \) になりません。
また,点 \( Q \) は \( B~G \) のどこかにしか動けないので,\( H \) に移動することはありません。
よって,\( ∠PAQ=60° \) になることはありません。
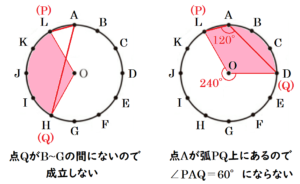
【 点 \( P \) が点 \( K \) に移動する(\( x=2 \))場合】
点 \( P \) が点 \( K \) に移動するとき,
\( ∠POQ=120° \) になるのは,
点 \( Q \) が点 \( C \) または \( G \) に移動するときなので,
両方があてはまり,\( (x,y)=(2,2),(2,6) \) の2通りです。
ただし,手順[1]で選んだカードは戻さないので,\( (x,y)=(2,2) \) が起こることはありません。
よって,あてはまるのは,\( (x,y)=(2,6) \) の1通りです。
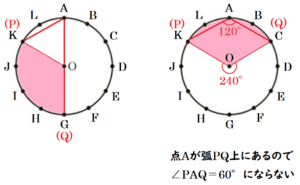
【 点 \( P \) が点 \( J \) に移動する(\( x=3 \))場合】
点 \( P \) が点 \( J \) に移動するとき,
\( ∠POQ=120° \) になるのは,
点 \( Q \) が点 \( B \) または \( F \) に移動するときなので,
両方があてはまり,\( (x,y)=(3,1),(3,5) \))の2通りです。
ただし,点 \( A \) が \( \stackrel{\huge\frown}{ PQ } \) 上(短い方)にあるので,
\( (x,y)=(3,1) \) のときには \( ∠PAQ=60° \) になりません。
よって,あてはまるのは,\( (x,y)=(3,5) \) の1通りです。
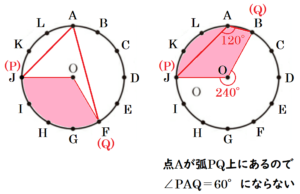
【 点 \( P \) が点 \( I \) に移動する(\( x=4 \))場合】
点 \( P \) が点 \( I \) に移動するとき,
\( ∠POQ=120° \) になるのは,
点 \( Q \) が点 \( A \) または \( E \) に移動するときです。
点 \( Q \) は \( B~G \) のどこかにしか動けないので,
あてはまるのは点 \( E \) に移動する(\( (x,y)=(4,4) \))場合の1通りだけです。
ただし,手順[1]で選んだカードは戻さないので,\( (x,y)=(4,4) \) が起こることはありません。
よって,あてはまる組み合わせはありません。
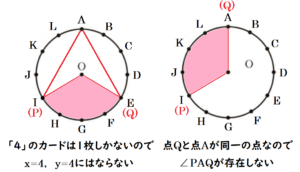
【 点 \( P \) が点 \( H \) に移動する(\( x=5 \))場合】
点 \( P \) が点 \( H \) に移動するとき,
\( ∠POQ=120° \) になるのは,
点 \( Q \) が点 \( D \) または \( L \) に移動するときです。
点 \( Q \) は \( B~G \) のどこかにしか動けないので,
あてはまるのは点 \( D \) に移動する(\( (x,y)=(5,3) \))場合の1通りだけです。
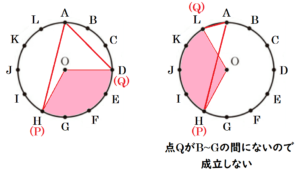
【 点 \( P \) が点 \( G \) に移動する(\( x=6 \))場合】
点 \( P \) が点 \( G \) に移動するとき,
\( ∠POQ=120° \) になるのは,
点 \( Q \) が点 \( C \) または \( K \) に移動するときです。
点 \( Q \) は \( B~G \) のどこかにしか動けないので,
あてはまるのは点 \( C \) に移動する(\( (x,y)=(6,2) \))場合の1通りだけです。
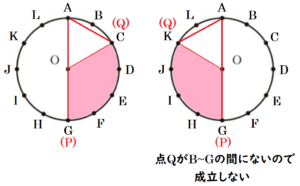
以上をまとめると,\( ∠PAQ=60° \) になる組み合わせは,
\( (x,y)=(2,6),(3,5),(5,3),(6,2) \)
の4通りになります。
よって,\( ∠PAQ=60° \) になる組み合わせは4通り,
全ての組み合わせは30通りなので,
求める確率は \( \dfrac{4}{30}=\dfrac{2}{15} \)
大問3
右の図のように,1辺の長さが \( 2 \; cm \) の正方形の紙Aと,1辺の長さが \( 1 \; cm \) の正方形の紙Bがある。
次の図のように,はじめに紙Aを1枚おき,その周りに紙Bをすき間なく並べて1番目の正方形を作る。次に,紙Aをたて,よこに2枚ずつすき間なく並べ,その周りにすき間なく紙Bを並べて2番目の正方形を作る。同様にして,紙Aをたて,よこに \( x \) 枚ずつすき間なく並べ,その周りにすき間なく紙Bを並べて \( x \) 番目の正方形を作る。このとき,次の問いに答えよ。
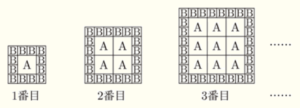
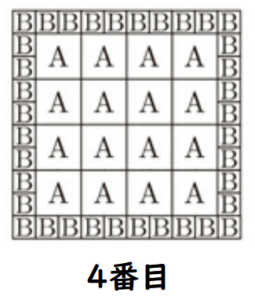
(1) \( 4 \) 番目の正方形は, 紙Aと紙Bがそれぞれ何枚並べられているか求めよ。
【解答】
紙A ・・・ \( 16 \) 枚
紙B ・・・ \( 36 \) 枚
【解説】
\( 4 \) 番目の正方形は,下の図のようになります。
(2) \( x \) 番目の正方形は, 紙Bが何枚並べられているか, \( x \) を用いて表せ。
【解説】
紙Aは,\( 1 \) 番目から \( 3 \) 番目までの図から,
\( 1 \)番目 ・・・ \( 1=1 \times 1 \)(枚)
\( 2 \)番目 ・・・ \( 4=2 \times 2 \)(枚)
\( 3 \)番目 ・・・ \( 9=3 \times 3 \)(枚)
と並んでいるので,\( x \) 番目の正方形は,紙Aがたてよこ \( x \) 枚ずつ並びます。
次に,紙Bを下の図のように4辺に均等な数になるよう分けて考えると,
\( 1 \) 番目から \( 3 \) 番目までの図から,1辺に並ぶ枚数は
\( 1 \)番目 ・・・ \( 3=2 \times 1+1 \)(枚)
\( 2 \)番目 ・・・ \( 5=2 \times 2+1 \)(枚)
\( 3 \)番目 ・・・ \( 7=2 \times 3+1 \)(枚)
となっているので,\( x \) 番目の正方形は,紙Bが各辺に \( 2x+1 \) 枚ずつ並びます。
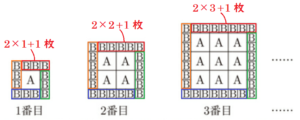
よって,紙Bは全部で
\( 4 \times (2x+1)=8x+4 \)(枚)
並びます。
(3) 紙Aと紙Bがあわせて \( 244 \) 枚並べられている正方形は、何番目の正方形か求めよ。
【解説】
(2)より,\( x \) 番目の正方形は,紙Aが \( x^2 \) 枚,紙Bが \( 8x+4 \) 枚並ぶので,
あわせて \( x^2+8x+4 \) 枚並ぶことになります。
よって,
\( x^2+8x+4=244 \)
\( x^2+8x-240=0 \)
\( (x-12)(x+20)=0 \)
\( x=12 \)(\( x>0 \) より)
となり,\( 12 \) 番目になります。
大問4
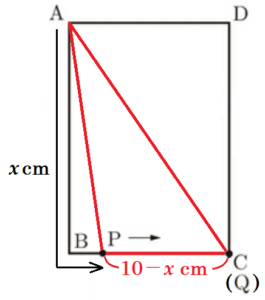
(1) 図1のような長方形 \( ABCD \) がある。点 \( P \) は点 \( A \) を出発して辺 \( AB \),辺 \( BC \) 上を毎秒 \( 1 \; cm \) で点 \( C \) まで動き,点 \( C \) で停止する。点 \( Q \) は,点 \( D \) を出発して辺 \( DC \) 上を毎秒 \( 1 \; cm \) で点 \( C \) まで動き,点 \( C \) で停止する。点 \( P,Q \) が同時に出発して \( x \) 秒後の \( △APQ \) の面積を \( S \; cm^2 \) とし,\( x \) と \( S \) の関係をグラフで表すと図2のようになった。ただし,\( △APQ \) ができないときは, \( S=0 \) とする。
このとき,次の問いに答えよ。
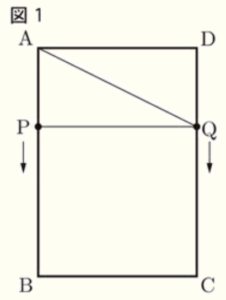
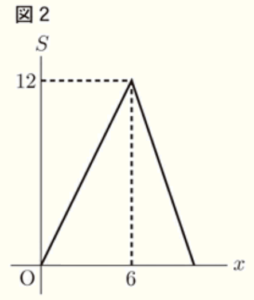
ア 辺 \( AB \),辺 \( BC \) の長さをそれぞれ求めよ。
【解答】
\( AB=6 \; cm \)
\( BC=4 \; cm \)
【解説】
底辺を \( PQ \),高さを \( AP \) と考えると,
点 \( P \) が辺 \( AB \) 上,点 \( Q \) が辺 \( DC \) 上を動くとき,
底辺の長さは一定で,高さが大きくなっていくので,
\( △APQ \) の面積は徐々に大きくなっていきます。
点 \( P \) が点 \( B \),点 \( Q \) が点 \( C \) につくとき,底辺も高さも最大になっているので,
\( △APQ \) の面積は最大になります。
また,グラフから,\( 6 \) 秒後に面積が最大になっていることから,
点 \( P \) は \( 6 \) 秒後に点 \( B \) につくことがわかります。
点 \( P \) は毎秒 \( 1 \; cm \) の速さで動くので,
辺 \( AB \) の長さは \( 6 \; cm \) ということになります。
また,\( 6 \) 秒後の \( △APQ \) の面積は \( 12 \; cm^2 \) であることから,
\( BC \times 6 \times \dfrac{1}{2}=12 \)
\( BC=4 \; (cm) \)
となります。
イ 点 \( P \) が辺 \( BC \) 上を動くとき,\( S \) を \( x \) を用いて表せ。また,そのときの \( x \) の変域を求めよ。
【解答】
\( S=-3x+30 \)(\( 6≦x≦10 \))
【解説】
まず,点 \( P \) が辺 \( BC \) 上を動くのは,点 \( B \) についてから,点 \( C \) につくまでの間です。
点 \( P \) が点 \( B \) につくのは,\( AB=6 \; cm \) より,\( 6 \) 秒後,
点 \( P \) が点 \( C \) につくのは,\( BC=4 \; cm \) より,さらに \( 4 \) 秒後なので \( 10 \) 秒後,
なので,\( x \) の変域は \( 6≦x≦10 \)
点 \( P \) が辺 \( BC \) 上を動くとき,
点 \( P \) は点 \( A \) から \( x \; cm \) 進んだ位置にあるので,\( AB+BP=x \; (cm) \) と表すことができます。
また,(1)より,\( AB+BC=10 \; (cm) \) なので,
\( PQ=(AB+BC)-(AB+BP) \)
\( =BC-BP \)
\( =10-x \; (cm) \)
よって,点 \( P \) が辺 \( BC \) 上を動くとき,
\( △APQ \) は底辺が \( (10-x) \; cm \)、高さが \( 6 \; cm \) になるので,
\( S=(10-x) \times 6 \times \dfrac{1}{2} \)
\( =3(10-x) \)
\( =-3x+30 \; (cm^2) \)
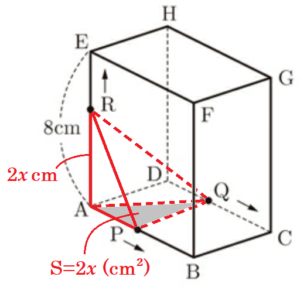
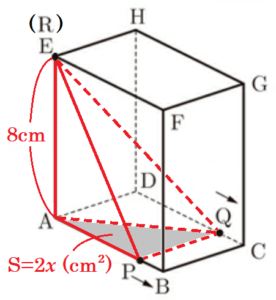
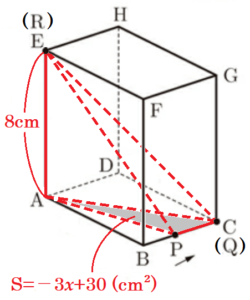
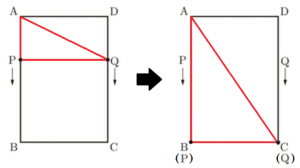
(2) 図3のような,(1)の長方形 \( ABCD \) を底面とし,高さ \( 8 \; cm \) の直方体 \( ABCD-EFGH \) がある。
点 \( P,Q \) は(1)と同じ動きをし,点 \( R \) は点 \( A \) を出発して辺 \( AE \) 上を毎秒 \( 2 \; cm \) で点 \( E \) まで動き,点 \( E \) で停止する。点 \( P,Q,R \) が同時に出発して \( x \) 秒後の三角錐 \( RAPQ \) の体積を \( V \; cm^3 \) とする。ただし,三角錐 \( RAPQ \) ができないときは, \( V=0 \) とする。このとき,次の問いに答えよ。
ア \( x \) と \( V \) の関係を表すグラフとして最も適当なものを,次の(a)~(d)から1つ選び,その記号を書け。
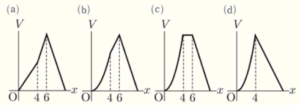
【解説】
点 \( R \) は \( 8 \; cm \) の辺 \( AE \) 上を毎秒 \( 2 \; cm \) で動くので,
点 \( R \) が点 \( E \) につくのは,\( 4 \) 秒後になります。
ここから,
点 \( P \) は辺 \( AB \) 上,点 \( Q \) は辺 \( DC \) 上,点 \( R \) は辺 \( AE \) 上を動く(\( 0≦x≦4 \))
点 \( P \) は辺 \( AB \) 上,点 \( Q \) は辺 \( DC \) 上を動き,点 \( R \) は点 \( E \) 上で動かない(\( 4≦x≦6 \))
点 \( P \) は辺 \( BC \) 上を動き,点 \( Q \) は点 \( C \) 上,点 \( R \) は点 \( E \) 上で動かない(\( 6≦x≦10 \))
となるので,それぞれの変域について \( V \) を \( x \) を用いて表していきます。
【\( 0≦x≦4 \) のとき】
点 \( R \) は毎秒 \( 2 \; cm \) で動くので,
\( AR \) の長さは \( 2x \; cm \) と表すことができ,
図2のグラフから,底面積 \( S=2x \; (cm) \) と
表すことができるので,
\( V=2x \times 2x \times \dfrac{1}{3} \)
\( =\dfrac{4}{3}x^2 \; (cm^3) \)
であり,グラフは放物線になります。
【\( 4≦x≦6 \) のとき】
点 \( R \) は点 \( E \) 上で動かないので,
\( AR=AE=8 \; cm \) で一定であり,
図2のグラフから,底面積 \( S=2x \; (cm) \) と
表すことができるので,
\( V=2x \times 8 \times \dfrac{1}{3} \)
\( =\dfrac{16}{3}x \; (cm^3) \)
であり,グラフは右上がりの直線になります。
【\( 6≦x≦10 \) のとき】
点 \( R \) は毎秒 \( 2 \; cm \) で動くので,
\( AR=AE=8 \; cm \) で一定であり,
(1)の問イから,底面積 \( S=-3x+30 \; (cm) \)
と表すことができるので,
\( V=(-3x+30) \times 8 \times \dfrac{1}{3} \)
\( =-8x+80 \; (cm^3) \)
であり,グラフは右下がりの直線になります。
よって,これらをすべて満たしているグラフは(b)になります。
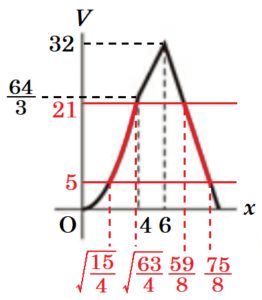
イ \( 5≦V≦21 \) となる \( x \) の値のうち,整数であるものをすべて求めよ。
【解説】
(b)のグラフにおいて,
\( x=4 \) のときの \( V \) の値は,
\( V=\dfrac{4}{3} \times 4^2=\dfrac{64}{3}(>\dfrac{63}{3}=21) \)
\( x=6 \) のときの \( V \) の値は,
\( V=\dfrac{16}{3} \times 6=32 \)
なので,(b)のグラフに \( V=5 \) と \( V=21 \) の
直線を書き加えると,右の図のようになります。
\( V=\dfrac{4}{3}x^2 \) と \( V=5 \) の交点の \( x \) 座標は,
\( 5=\dfrac{4}{3}x^2 \)
\( x^2=\dfrac{15}{4} \)
\( x=\sqrt{\dfrac{15}{4}} \)(\( x>0 \) より)
\( V=\dfrac{4}{3}x^2 \) と \( V=21 \) の交点の \( x \) 座標は,
\( 21=\dfrac{4}{3}x^2 \)
\( x^2=\dfrac{63}{4} \)
\( x=\sqrt{\dfrac{63}{4}} \)(\( x>0 \) より)
\( V=-8x+80 \) と \( V=21 \) の交点の \( x \) 座標は,
\( 21=-8x+80 \)
\( 8x=59 \)
\( x=\dfrac{59}{8} \)
\( V=-8x+80 \) と \( V=5 \) の交点の \( x \) 座標は,
\( 5=-8x+80 \)
\( 8x=75 \)
\( x=\dfrac{75}{8} \)
なので,\( 5≦V≦21 \) となる \( x \) の変域は \( \sqrt{\dfrac{15}{4}}≦x≦\sqrt{\dfrac{63}{4}},\dfrac{59}{8}≦x≦\dfrac{75}{8} \) となります。
\( (1=)\sqrt{\dfrac{4}{4}}<\sqrt{\dfrac{15}{4}}<\sqrt{\dfrac{16}{4}}(=2) \) なので,\( \sqrt{\dfrac{15}{4}}=1. \)○○,
\( (3=)\sqrt{\dfrac{36}{4}}<\sqrt{\dfrac{63}{4}}<\sqrt{\dfrac{64}{4}}(=4) \) なので,\( \sqrt{\dfrac{63}{4}}=3. \)○○,
であり,\( \sqrt{\dfrac{15}{4}}≦x≦\sqrt{\dfrac{63}{4}} \) を満たす \( x \) の値のうち,整数は \( 2,3 \)。
\( (7=)\dfrac{56}{8}<\dfrac{59}{8}<\dfrac{64}{8}(=8) \) なので,\( \dfrac{59}{8}=7. \)○○,
\( (9=)\dfrac{72}{8}<\dfrac{75}{8}<\dfrac{80}{8}(=10) \) なので,\( \dfrac{75}{8}=9. \)○○,
であり,\( \dfrac{59}{8}≦x≦\dfrac{75}{8} \) を満たす \( x \) の値のうち,整数は \( 8,9 \)。
以上より,\( 5≦V≦21 \) となる \( x \) の値のうち,整数であるものは \( 2,3,8,9 \)
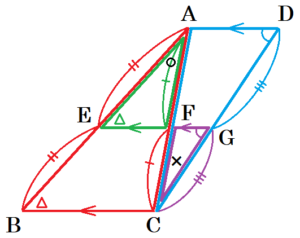
大問5
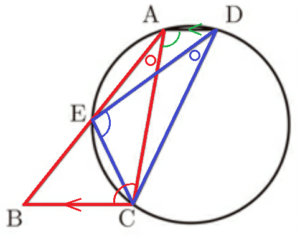
右の図のような台形 \( ABCD \) があり,\( AD // BC \) である。また,3点 \( A,C,D \) を通る円と辺 \( AB \) は,点 \( A,B \) と異なる点で交わり,その交点を \( E \) とする。このとき,次の問いに答えよ。
(1) \( △ABC \) ∽ \( △DCE \) を証明せよ。
【解答】
\( △ABC \) と \( △DCE \) において,
\( \stackrel{\huge\frown}{ CE } \) に対する円周角なので,
\( ∠BAC=∠CDE \) ・・・ ➀
\( AD // BC \) より錯角は等しいので,
\( ∠BCA=∠CAD \) ・・・ ➁
\( \stackrel{\huge\frown}{ CD } \) に対する円周角なので,
\( ∠CED=∠CAD \) ・・・ ➂
➁➂より,\( ∠BCA=∠CED \) ・・・ ➃
➀➃より,2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △DCE \)
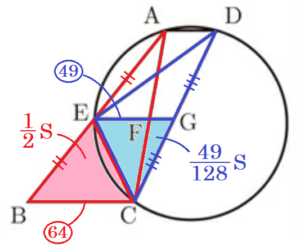
(2) さらに,点 \( E \) を通り,直線 \( BC \) に平行な直線と,辺 \( AC,DC \) の交点をそれぞれ \( F,G \) とする。点 \( E \) が辺 \( AB \) の中点で,\( AB:DC=8:7 \) のとき,次の問いに答えよ。
ア \( △ABC \) の面積を \( S \) とおくとき,\( △DEG \) の面積を \( S \) を用いて表せ。また,その求め方を言葉や数,式などを用いて説明せよ。
【解答】
(1)より,\( △ABC \) ∽ \( △DCE \) であり,
\( AB:DC=8:7 \) より,面積比は \( 64:49 \) である。
ここから,\( △DCE \) の面積は
\( △ABC:△DCE=64:49 \)
\( S:△DCE=64:49 \)
\( △DCE=\dfrac{49}{64}S \)
また,\( AD//BC//EG \),
点 \( E \) が辺 \( AB \) の中点であることから,点 \( G \) は辺 \( DC \) の中点なので,
\( △DEG \) の面積は \( △DCE \) の面積の \( \dfrac{1}{2} \) である。
よって,\( △DEG \) の面積は
\( △DEG=\dfrac{1}{2} \times \dfrac{49}{64}S=\dfrac{49}{128}S \)
【解説】
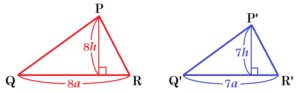
【相似な三角形の面積比は相似比の2乗の比と等しい】
底辺が \( 8a \),高さが \( 8h \) の \( △PQR \) において,
\( △PQR \) ∽ \( △P’Q’R’ \) で相似比が \( 8:7 \) のとき,
\( △P’Q’R’ \) の底辺は \( 7a \),高さは \( 7h \) と表すことができます。
このとき,\( △PQR,△P’Q’R’ \) の面積は,
\( △PQR=8a \times 8h \times \dfrac{1}{2} \)
\( △P’Q’R’=7a \times 7h \times \dfrac{1}{2} \)
で求められるので,
\( △PQR:△P’Q’R’=8a \times 8h \times \dfrac{1}{2}:7a \times 7h \times \dfrac{1}{2} \)
\( =8 \times 8:7 \times 7 \)
\( =8^2:7^2 \)
【点 \( E \) が辺 \( AB \) の中点のとき,点 \( G \) は辺 \( DC \) の中点である】
\( △ABC \) と \( △AEF \) において,
\( AD//BC//EG \) より同位角は等しいので,
\( ∠ABC=∠AEF \) ・・・ ➀
共通な角なので,
\( ∠BAC=∠EAF \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △AEF \)
対応する辺の比は等しいので,
\( AC:AF=AB:AE=2:1 \)
であり,点 \( F \) は辺 \( AC \) の中点である。
同様の考え方から,\( △CDA \) ∽ \( △CGF \) でもあるので,
点 \( G \) は辺 \( DC \) の中点である。
イ \( AD:BC \) を最も簡単な整数の比で表せ。
【解説】
\( △ABC \) において,点 \( E \) が辺 \( AB \) の中点なので,
\( △EBC \) の面積は \( △ABC \) の面積の \( \dfrac{1}{2} \) であり,
\( \dfrac{1}{2}S \) と表すことができます。
同様に,点 \( G \) は辺 \( DC \) の中点なので,
\( △CEG \) の面積は \( △CEG=△DEG=\dfrac{49}{128}S \)
と表すことができます。
\( △EBC \) の底辺を \( BC \),\( △CEG \) の底辺を \( EG \) とすると,
高さが共通なので,\( BC:EG \) の比は,\( △EBC \) と \( △CEG \) の面積比と等しくなります。
ここから,
\( BC:EG=\dfrac{1}{2}S:\dfrac{49}{128}S \)
\( =64:49 \)
また,\( AD//BC//EG \),点 \( E \) が辺 \( AB \) の中点,
点 \( G \) が辺 \( DC \) の中点であることから,
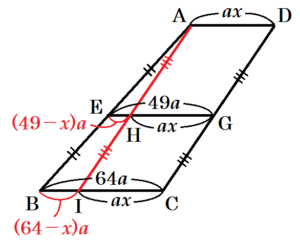
\( AD:EG:BC=x:49:64 \) とすると.
\( \dfrac{x+64}{2}=49 \)
\( x+64=98 \)
\( x=34 \)(注1)
よって,\( AD:BC=34:64=17:32 \)
AD:EG:BCの求め方
\( AD:EG:BC=x:49:64 \) より,\( AD=ax,EG=49a,BC=64a \) とします。
点 \( A \) を通り,辺 \( DC \) と平行な線分と
辺 \( EG,BC \) の交点を \( H,I \) とすると,
\( △ABI \) ∽ \( △AEH \),相似比 \( 2:1 \) になっています。
ここから,\( BI:EH=2:1 \) なので,
\( (64-x)a=2(49-x)a \)
\( 64-x=2 \times 49-2x \)
\( 64+x=2 \times 49 \)
\( \dfrac{x+64}{2}=49 \)
(以下省略)