大問1
(1) 次の計算をしなさい。
1 \( (-4) \times (-7) \)
2 \( -\dfrac{1}{6}+\dfrac{1}{3} \)
【解説】
\( =-\dfrac{1}{6}+\dfrac{2}{6} \)
\( =\dfrac{1}{6} \)
3 \( (-2a)^3 \times 2b \)
【解説】
\( =-8a^3 \times 2b \)
\( =-16a^3b \)
4 \( \sqrt{12}+\sqrt{3} \)
【解説】
\( =2\sqrt{3}+\sqrt{3} \)
\( =3\sqrt{3} \)
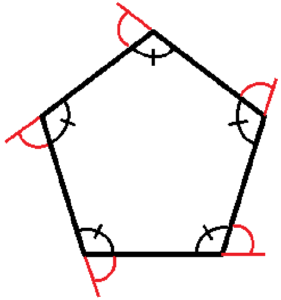
(2) 正五角形の1つの外角の大きさを求めなさい。
【解説】
多角形の外角の和は必ず \( 360° \) になります。
また,正五角形の内角はすべて等しいので,
外角もすべて等しくなっています。
よって,正五角形の1つの外角の大きさは,
\( 360° \div 5=72° \)
大問2
(1) 1本 \( 80 \) 円のえんぴつを \( a \) 本買うのに,500円玉1枚を出した。このときのおつりを,\( a \) を使った式で表しなさい。ただし,消費税は考えないものとする。
【解説】
1本 \( 80 \) 円のえんぴつを \( a \) 本の代金は \( 80a \) 円なので,
\( 500 \) 円払ったときのおつりは,\( 500-80a \)(円)と表すことができます。
(2) \( y \) が \( x \) の1次関数で,変化の割合が \( 2 \) で,\( x=-3 \) のとき \( y=7 \) となる1次関数の式を求めなさい。
【解説】
1次関数を表す式は \( y=ax+b \)(\( a,b \) は定数)であり,
変化の割合が \( 2 \) のときは,\( y=2x+b \) になります。
ここに,\( x=-3,y=7 \) を代入すると,
\( 7=2 \times (-3)+b \)
\( 7=-6+b \)
\( b=13 \)
よって,求める式は \( y=2x+13 \) になります。
(3) \( x^2-3x-10 \) を因数分解しなさい。
(4) 半径 \( 3 \; cm \) の球と底面の半径が \( 6 \; cm \) の円錐がある。球と円錐の体積が等しいとき,この円錐の高さを求めなさい。
【解説】
円錐の高さを \( h \; cm \) とするとき,
底面の半径が \( 6 \; cm \) の円錐の体積は,
\( (\pi{} \times 6^2) \times h \times \dfrac{1}{3}=12\pi{}h \; (cm^3) \)
と表すことができます。
半径 \( 3 \; cm \) の球の体積は,
\( \dfrac{4\pi{} \times 3^3}{3}=36\pi{} \; (cm^3) \)
と表すことができます。
これらの体積が等しいとき,
\( 12\pi{}h=36\pi{} \; (cm^3) \)
\( h=3 \; (cm) \)
(5) ある学級の生徒 \( 33 \) 人が,6月,9月,12月にそれぞれ1回ずつ \( 50 \) 点満点の数学のテストを受けた。
下の図は,6月,9月,12月に受けた数学のテストの得点の分布のようすを箱ひげ図に表したものである。
このとき,箱ひげ図から読みとれることとして正しいものを,次のア~エの中から1つ選び,記号で答えなさい。
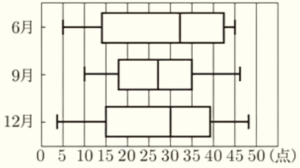
ア 範囲が最も大きいのは,9月である。
イ 四分位範囲は,6月より12月のほうが大きい。
ウ 6月,9月,12月のテストの得点の合計が \( 135 \) 点以上の生徒がかならずいる。
エ 6月のテストの得点が \( 40 \) 点以上の生徒は \( 8 \) 人以上いる。
【解説】
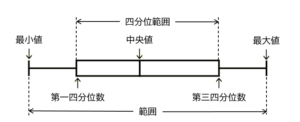
ア 範囲は「最大値 \( – \) 最小値」で求められます。
6月 ・・・ \( 45-5=40 \)(点)
9月 ・・・ \( 46-10=36 \)(点)
12月 ・・・ \( 48-4=44 \)(点)
となるので,最も大きいのは12月になります。
イ 四分位範囲は「第三四分位数 \( – \) 第一四分位数」で求められます。
6月 ・・・ \( 42-14=28 \)(点)
12月 ・・・ \( 39-15=24 \)(点)
となるので,6月の方が大きくなっています。
ウ 箱ひげ図のデータからだけでは,複数の箱ひげ図における個人のデータの合計値を特定することは
できません。
エ \( 33 \) 人のデータを集計しているので,第三四分位数は大きい方から8番目と9番目の平均値に
なります。
6月の箱ひげ図の第三四分位数は \( 42 \) 点なので,得点が高い方から8番目の人の得点は
\( 42 \) 点以上になっています。
よって,得点が \( 40 \) 点以上の生徒は \( 8 \) 人以上いるとわかります。
大問3
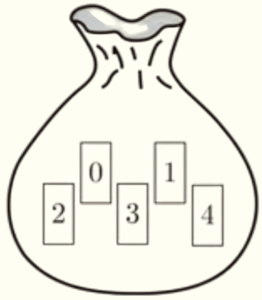
(1) 右の図のように,袋の中に \( 0,1,2,3,4 \) の数字が1つずつ書かれた5枚のカードが入っている。
この袋の中からカードを1枚取り出し,そのカードに書かれた数を \( a \) とする。次に,その取り出したカードを袋の中にもどさず,残り4枚のカードから1枚取り出し,そのカードに書かれた数を \( b \) とする。
ただし,どのカードを取り出すことも同様に確からしいものとする。
1 \( ab+a=3 \) となる場合は何通りあるか求めなさい。
【解説】
選んだカードの数 \( a,b \) の組み合わせとそれぞれの場合の \( ab+a=3 \) の値を樹形図にして書き出すと,
下の図のようになり,\( ab+a=3 \) となる場合は2通りになります。
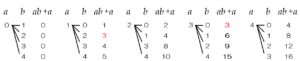
2 \( ab+a \) の値が偶数となる確率を求めなさい。
【解説】
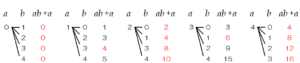
下の樹形図から,すべての場合は20通り,\( ab+a \) の値が偶数となる場合は14通りなので,
その確率は,\( \dfrac{14}{20}=\dfrac{7}{10} \)
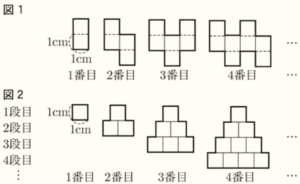
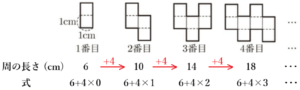
(2) 次の図1,図2のように,1辺が \( 1 \; cm \) の正方形を用いて,1番目,2番目,3番目,4番目,・・・ と,規則正しく並べて図形をつくっていく。
図1は,正方形を縦に2個並べた長方形を,1番目は1個,2番目は2個,3番目は3個,4番目は4個のように,長方形の縦の辺が \( 1 \; cm \) ずつ上下を交互に重なるように並べていったものである。
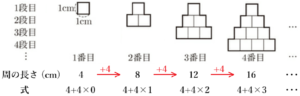
図2は,正方形を,1番目は1個,2番目は3個,3番目は6個,4番目は10個のように,2番目の図形以降では,1段増やすごとに,その段の数と同じ個数の正方形を加え,三角形の形になるようにすきまなく並べていったものである。
なお,図1,図2それぞれの太い線(ー)の長さを図形の周の長さとする。
1 図1の4番目の図形の周の長さから図2の4番目の図形の周の長さをひいたときの差を求めなさい。
【解説】
図1の4番目の図形の周の長さは \( 18 \; cm \),
図2の4番目の図形の周の長さは \( 16 \; cm \),
なので,差は \( 2 \; cm \) になっています。
2 図1の \( n \) 番目の図形の周の長さを \( K \; cm \),図2の \( n \) 番目の図形の周の長さを \( L \; cm \) とする。\( K \) から \( L \) をひいたときの差について,どのようなことがいえるか。次のア~ウの中から正しいものを1つ選び,記号で答えなさい。また,\( K,L \) を,それぞれ \( n \) を使った式で表し,選んだものが正しい理由を説明しなさい。ただし,\( n \) は自然数とする。
ア 正の数になることも,負の数になることもある。
イ 一定である。
ウ \( 10 \) より大きくなることもある。
【解答】
イ 一定である。
【正しい理由】
図1の \( n \) 番目の図形の周の長さ \( K \; cm \) を \( n \) を使った式で表すと,
\( K=4n+2 \; (cm) \)
図2の \( n \) 番目の図形の周の長さ \( L \; cm \) を \( n \) を使った式で表すと,
\( L=4n \; (cm) \)
と表すことができるので,
\( K-L=(4n+2)-4n=2 \; (cm) \)
であり,\( K \) から \( L \) をひいたときの差は一定である。
【解説】
【\( K \; cm \) を \( n \) を使った式で表す】
図1の4番目までの周の長さを数えていくと,
\( 6 \; cm \) → \( 10 \; cm \) →\( 14 \; cm \) →\( 18 \; cm \) ・・・
と \( 4 \; cm \) ずつ増えていて,それぞれの長さを
\( 6+4 \times 0 \; cm \) → \( 6+4 \times 1 \; cm \) →\( 6+4 \times 2 \; cm \) →\( 6+4 \times 3 \; cm \) ・・・
と考えると,\( n \) 番目の図形の周の長さ \( K \; cm \) は
\( K=6+4(n-1)=4n+2 \; (cm) \)
と表すことができます。
【\( L \; cm \) を \( n \) を使った式で表す】
図2の4番目までの周の長さを数えていくと,
\( 4 \; cm \) → \( 8 \; cm \) →\( 12 \; cm \) →\( 16 \; cm \) ・・・
と \( 4 \; cm \) ずつ増えていて,それぞれの長さを
\( 4+4 \times 0 \; cm \) → \( 4+4 \times 1 \; cm \) →\( 4+4 \times 2 \; cm \) →\( 4+4 \times 3 \; cm \) ・・・
と考えると,\( n \) 番目の図形の周の長さ \( L \; cm \) は
\( L=4+4(n-1)=4n \; (cm) \)
と表すことができます。
大問4
ひろとさんは,家族旅行の計画を立てるために,自家用車で自宅から目的地に着くまでの時間と道のりについて調べ,次の<メモ>にまとめた。
ただし,<メモ>は高速道路を時速 \( 90 \; km \),ふつうの道路を時速 \( 40 \; km \) で走ると仮定したときのものである。
<メモ>
・ 自宅から目的地に着くまでの時間は,全体で \( 3.5 \) 時間である。
・ 自宅から目的地に着くまでの道のりは,全部で \( 280 \; km \) である。
このとき,高速道路を走る時間とふつうの道路を走る時間は,それぞれ何時間か,求めなさい。
また,求める過程も書きなさい。
【解答】
高速道路を走る時間 ・・・ \( 2.8 \) 時間
ふつうの道路を走る時間 ・・・ \( 0.7 \) 時間
【解説】
高速道路を走る時間を \( x \) 時間,ふつうの道路を走る時間を \( y \) 時間とすると,
時間の関係を表す式は \( x+y=3.5 \) ・・・ ➀
道のりの関係を表す式は \( 90x+40y=280 \) ・・・ ➁
と表すことができる。
➀➁を連立方程式として解くと,
\( \left\{ \begin{array}{}
x+y=3.5 \;\; ・・・ \;\; ➀ \\
90x+40y=280 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
より
\( x=2.8,y=0.7 \)
よって,
高速道路を走る時間は \( 2.8 \) 時間
ふつうの道路を走る時間は \( 0.7 \) 時間
【途中式】
\( \left\{ \begin{array}{}
x+y=3.5 \;\; ・・・ \;\; ➀ \\
90x+40y=280 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁を整理すると,
\( 9x+4y=28 \) ・・・ ➁’
➀ \( \times 4 \) すると,
\( 4x+4y=14 \) ・・・ ➀’
➁’\( – \)➀’
\( 5x=14 \)
\( x=2.8 \)
➀に代入すると,
\( 2.8+y=3.5 \)
\( y=0.7 \)
大問5
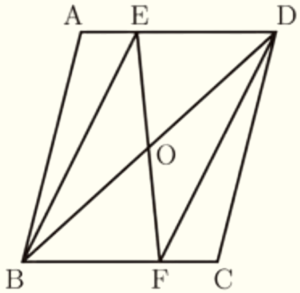
右の図において,四角形 \( ABCD \) は平行四辺形であり,点 \( O \) は対角線 \( BD \) の中点である。辺 \( AD \) 上に点 \( E \) をとり,直線 \( EO \) と辺 \( BC \) との交点を \( F \) とする。
次の[証明]は,\( △ABE≡△CDF \) となることを証明したものである。
このとき,次の(1),(2)の問いに答えなさい。
[証明]
\( △OBF \) と \( △ODE \) において
仮定から \( OB=OD \) ・・・ ➀
対頂角は等しいから \( ∠BOF=∠DOE \) ・・・ ➁
\( AD//BC \) より,平行線の Ⅰ は等しいから
\( ∠OBF=∠ODE \) ・・・ ➂
➀,➁,➂ より, Ⅱ がそれぞれ等しいから
\( △OBF≡△ODE \)
合同な図形の対応する辺は等しいから
\( BF=DE \) ・・・ ➃
Ⅲ
(1) Ⅰ , Ⅱ にあてはまることばの組み合わせとして正しいものを,次のア~エの中から1つ選び,記号で答えなさい。
ア Ⅰ 同位角 Ⅱ 1組の辺とその両端の角
イ Ⅰ 同位角 Ⅱ 2組の辺とその間の角
ウ Ⅰ 錯角 Ⅱ 1組の辺とその両端の角
エ Ⅰ 錯角 Ⅱ 2組の辺とその間の角
【解答】
ウ Ⅰ 錯角 Ⅱ 1組の辺とその両端の角
【解説】
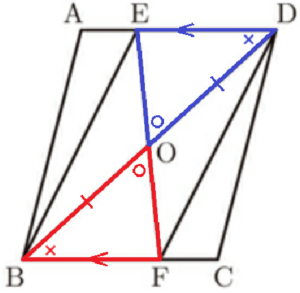
➀,➁,➂を図中に書き込むと次のようになります。
(2) Ⅲ に証明の続きを書き,[証明]を完成させなさい。
ただし,[証明]の中の➀~➃に示されている関係を使う場合は,番号の➀~➃を用いてもよい。また,新たな関係に番号をつける場合は,➄以降の番号を用いなさい。
【解答】
\( △ABE \) と \( △CDF \) において
平行四辺形の向かい合う辺の長さは等しいので,
\( AD=CB \) ・・・ ➄
\( AB=CD \) ・・・ ⑥
また,
\( AE=AD-DE \) ・・・ ➆
\( CF=CB-BF \) ・・・ ⑧
➃➄➆➇より,
\( AE=CF \) ・・・ ➈
平行四辺形の向かい合う角の大きさは等しいので,
\( ∠BAE=∠DCF \) ・・・ ➉
⑥➈➉より,
2組の辺とその間の角がそれぞれ等しいので,
\( △ABE≡△CDF \)
【解説】
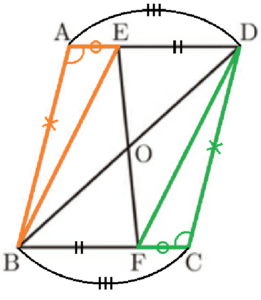
➄~➉を図中に書き込むと次のようになります。
大問6
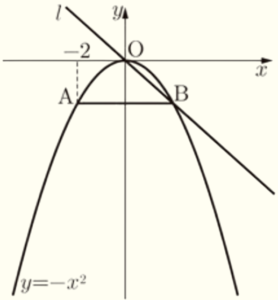
右の図のように,関数 \( y=-x^2 \) のグラフ上に2点 \( A,B \) がある。\( A \) の \( x \) 座標は \( -2 \) であり,線分 \( AB \) は \( x \) 軸に平行である。また,2点 \( O,B \) を通る直線を \( l \) とする。
このとき,次の(1),(2)の問いに答えなさい。
(1) 点 \( A \) の \( y \) 座標を求めなさい。
【解説】
点 \( A \) は \( y=-x^2 \) 上の点で,\( x \) 座標が \( -2 \) なので,
\( y=-(-2)^2=-4 \)
(2) 関数 \( y=-x^2 \) のグラフ上に点 \( C \) をとり,\( C \) の \( x \) 座標を \( t \) とする。ただし,\( t<-2 \) とする。
また,\( C \) を通り \( x \) 軸に平行な直線と \( l \) との交点を \( D \) とする。
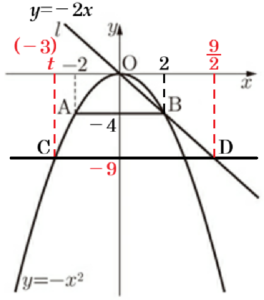
1 \( t=-3 \) のとき,点 \( D \) の \( x \) 座標を求めなさい。
【解説】
\( t=-3 \) のとき,点 \( C \) は \( y=-x^2 \) 上の点で,
\( x \) 座標が \( -3 \) なので,\( y \) 座標は,
\( y=-(-3)^2=-9 \)
また,(1)より点 \( B \) は \( y=-x^2 \) 上の点で,
\( y \) 座標が \( -4 \) なので,\( x \) 座標は,
\( -4=-x^2 \)
\( x=2 \)(\( x>0 \) より)
ここから,直線 \( l \) は原点と \( B(2,-4) \) を通るので,直線 \( l \) の式は,\( y=-2x \) です。
点 \( D \) は \( y=-2x \) 上の点で,
\( y \) 座標が \( -9 \) なので,\( x \) 座標は,
\( -9=-2x \)
\( x=\dfrac{9}{2} \)
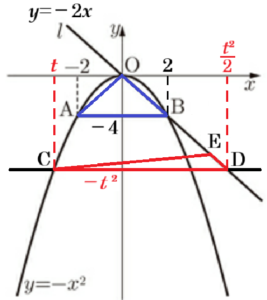
2 線分 \( OD \) 上に \( DE=\sqrt{5} \) となる点 \( E \) をとる。\( △CDE \) の面積が \( △OAB \) の面積と等しくなるときの \( t \) の値を求めなさい。
【解説】
点 \( C \) の \( x \) 座標が \( t \) のとき,
\( y \) 座標は \( -t^2 \) と表すことができます。
このとき,点 \( D \) は \( y=-2x \) 上の点で,
\( y \) 座標が \( -t^2 \) なので,\( x \) 座標は,
\( -t^2=-2x \)
\( x=\dfrac{t^2}{2} \)
と表すことができます。
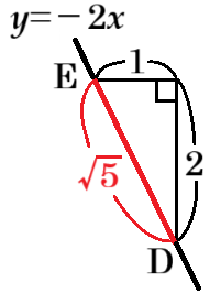
また,\( DE=\sqrt{5} \) となるとき,\( DE \) を斜辺とする
直角三角形を考えると,直角をなす2辺の長さは
\( 1 \) と \( 2 \) になります。
点 \( D,E \) が \( y=-2x \) 上の点であることから,
点 \( E \) は \( x \) 座標が点 \( D \) より \( 1 \) 小さく,
\( y \) 座標が点 \( D \) より \( 2 \) 大きい点になります。
以上より,\( △CDE \) の底辺を \( CD \) とすると,\( △CDE \) の面積は,
\( △CDE=\left( \dfrac{t^2}{2}-t \right) \times 2 \times \dfrac{1}{2} \)
\( =\dfrac{t^2}{2}-t \)
と表すことができ,
\( △OAB \) の面積は,
\( △OAB=4 \times 4 \times \dfrac{1}{2}=8 \)
になります。
以上より,\( △CDE \) の面積が \( △OAB \) の面積と等しくなるとき,
\( \dfrac{t^2}{2}-t=8 \)
\( t^2-2t=16 \)
\( t^2-2t-16=0 \)
\( t=\dfrac{-(-2)±\sqrt{(-2)^2-4 \times 1 \times (-16)}}{2 \times 1} \)
\( =\dfrac{2±\sqrt{68}}{2} \)
\( =1-\sqrt{17} \) (\( t<-2 \) より)
大問7
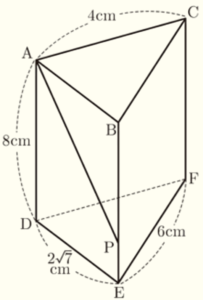
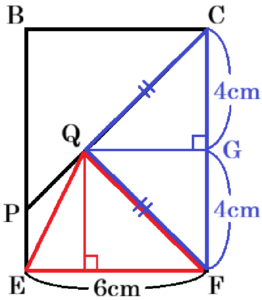
右の図のような,底面が \( AB=DE=2\sqrt{7} \; cm \),
\( BC=EF=6 \; cm,AC=DF=4 \; cm \) の
三角形で,高さが \( 8 \; cm \) の三角柱がある。
なお,\( △DEF \) の3つの角はすべて鋭角である。
辺 \( BE \) 上に \( AD=AP \) となる点 \( P \) をとる。
このとき,次の(1),(2)の問いに答えなさい。
(1) 線分 \( BP \) の長さを求めなさい。
【解説】
\( AP=AD=8 \; cm,AB=DE=2\sqrt{7} \; cm \) なので,
\( △ABP \) において,三平方の定理より,
\( BP^2=8^2-(2\sqrt{7})^2=36 \)
\( BP=6 \; (cm) \)( \( BP>0 \) より)
(2) 線分 \( CP \) 上に \( QC=QF \) となる点 \( Q \) をとる。
1 \( △QEF \) の面積を求めなさい。
【解答】
\( △QEF=12 \; cm^2 \)
【解説】
面 \( BEFC \) に注目すると,\( QC=QF \) より
\( △QCF \) は二等辺三角形になっています。
点 \( Q \) から線分 \( CF \) に垂線をひいた交点を \( G \) と
すると,点 \( G \) は線分 \( CF \) の中点なので,
\( CF=AD=8 \; cm \) より \( GF=4 \; cm \) になっています。
\( △QEF \) の底辺を \( EF \) とすると,
高さは \( GF \) と等しいので,
\( △QEF \) の面積は,
\( △QEF=6 \times 4 \times \dfrac{1}{2}=12 \; (cm^2) \)
2 \( D \) を頂点とし,四角形 \( EFQP \) を底面とする四角錐の体積を求めなさい。
【解答】
\( \dfrac{28\sqrt{3}}{3} \; cm^3 \)
【解説】
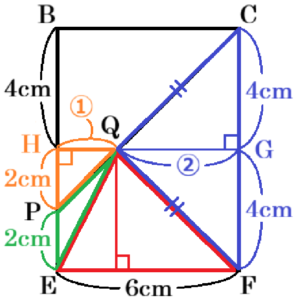
底面の四角形 \( EFQP \) を \( △QEF \) と \( △QEP \) に分けて考えます。
点 \( Q \) から線分 \( BE \) に垂線をひいた交点を \( H \) と
すると,\( BH=CG=4 \; cm \) であり,\( BP=6 \; cm \) であることから,
\( PH=6-4=2 \; (cm) \)
\( △QPH \) ∽ \( △QCG \) であり,
対応する辺の比は等しいので,
\( HQ:QG=PH:CG=1:2 \)
\( HG=EF=6 \; cm \) なので,
\( HQ=\dfrac{1}{3}HG=2 \; (cm) \)
また,\( BE=AD=8 \; cm,BP=6 \; cm \) より \( PE=2 \; cm \) なので,
\( △QEP \) の面積は,
\( △QEP=2 \times 2 \times \dfrac{1}{2}=2 \; (cm^2) \)
よって,底面の四角形 \( EFQP \) の面積は,
\( △QEF+△QEP=12+2=14 \; (cm^2) \)
次に,四角すいの高さを求めます。
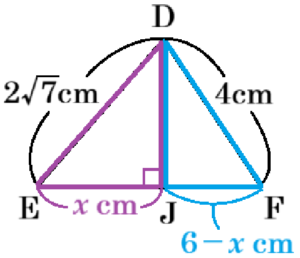
\( △DEF \) で,点 \( D \) から線分 \( EF \) に垂線を
ひいた交点を \( J \) とし,\( EJ=x \; cm \) とすると,
\( △DEJ \) と \( △DFJ \) において,
三平方の定理より,
\( DE^2-EJ^2=DF^2-FJ^2 \)
\( (2\sqrt{7})^2-x^2=4^2-(6-x)^2 \)
\( 28-x^2=16-(36-12x+x^2) \)
\( x=4 \)
なので,
\( DJ^2=(2\sqrt{7})^2-4^2=12 \)
\( DJ=2\sqrt{3} \; (cm) \)( \( EJ>0 \) より)
以上より,求める四角すいの体積は,
\( 14 \times 2\sqrt{3} \times \dfrac{1}{3}=\dfrac{28\sqrt{3}}{3} \; (cm^3) \)