大問1
下の(1)~(5)に答えなさい。
(1) 次のア~オの計算をしなさい。
ア \( 5-(-4) \)
【解答&解説】
\( =5+4 \)
\( =9 \)
イ \( (-3)^2 \times 2-8 \)
【解答&解説】
\( =9 \times 2-8 \)
\( =18-8 \)
\( =10 \)
ウ \( \dfrac{15}{2}x^3y^2 \div \dfrac{5}{8}xy^2 \)
【解答&解説】
\( =\dfrac{15x^3y^2}{2} \times \dfrac{8}{5xy^2} \)
\( =\dfrac{15x^3y^2 \times 8}{2 \times 5xy^2} \)
\( =12x^2 \)
エ \( \dfrac{4a-2b}{3}-\dfrac{3a+b}{4} \)
【解答&解説】
\( =\dfrac{4(4a-2b)}{12}-\dfrac{3(3a+b)}{12} \)
\( =\dfrac{4(4a-2b)-3(3a+b)}{12} \)
\( =\dfrac{16a-8b-9a-3b}{12} \)
\( =\dfrac{7a-11b}{12} \)
オ \( \sqrt{54}-2\sqrt{3} \div \sqrt{2} \)
【解答&解説】
\( =3\sqrt{6}-\dfrac{2\sqrt{3}}{\sqrt{2}} \)
\( =3\sqrt{6}-\sqrt{6} \)
\( =2\sqrt{6} \)
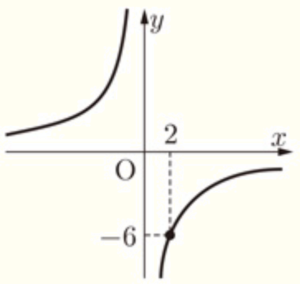
(2) 右の図は,反比例のグラフ である。\( y \) を \( x \) の式で表しなさい。
【解答】
\( y=-\dfrac{12}{x} \)
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \) (\( a \) は定数) です。
ここに,\( x=2,y=-6 \) を代入すると,
\( -6=\dfrac{a}{2} \)
\( a=-12 \)
よって,求める式は,\( y=-\dfrac{12}{x} \)
(3) \( \sqrt{60n} \) が自然数になるような自然数 \( n \) のうちで,最も小さい値を求めなさい。
【解説】
\( \sqrt{60n} \) が自然数になるということは, \( 60n \) が平方数になるということです。
\( 60n \) を因数分解すると,
\( 60n=2^2 \times 3 \times 5 \times n \)
平方数は素因数分解すると,すべての素因数が偶数乗になります。
つまり,今回の場合だと,\( 3 \) と \( 5 \) を もっとも小さい偶数乗(2乗)に
すればよいので,\( n=3 \times 5=15 \)
(4) \( a \; mL \) のジュースを7人に \( b mL \) ずつ分けたら,残り \( 200 mL \) より少なくなった。このときの数量の間の関係を,不等式で表しなさい。
【解答&解説】
ジュースを7人に \( b mL \) ずつ分けるとき必要な量 → \( 7b \)
残ったジュースの量を文字式で表すと,\( a-7b \)
これが,\( 200 \; mL \) より少なかったので,
\( a-7b<200 \)
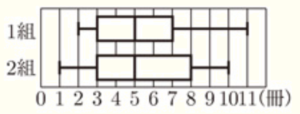
(5) A中学校の3年1組と2組の生徒それぞれ31人について,ある期間に読んだ本の冊数を調べた。右の図は,その分布のようすを箱ひげ図に表したものである。
このとき,次の ア~オ のうち,箱ひげ図から読みとれることとして正しいものを2つ選び,その符号を書きなさい。
ア 1組と2組の平均値は等しい。
イ 2組の第3四分位数のほうが,1組の第3四分位数より大きい。
ウ どちらの組もデータの四分位範囲は9冊である。
エ どちらの組にも,読んだ本が7冊以上の生徒は8人以上いる。
オ どちらの組にも,読んだ本が10冊の生徒が必ずいる。
【解説】
ア 箱ひげ図だけから平均値はわかりません。
イ 1組の第3四分位数は \( 7 \) 冊,2組の第3四分位数は \( 8 \) 冊
ウ 1組の第3四分位数 \( =7-3=4 \)冊,2組の第3四分位数 \( =8-3=5 \)冊
エ 1組,2組ともに生徒数は31人なので,第3四分位数になるのは,多い方から8番目の人の冊数。
1組の第3四分位数は \( 7 \) 冊,2組の第3四分位数は \( 8 \) 冊なので,
7冊以上の生徒はどちらにも8人以上います。
オ 2組は,最大値が10冊なので,読んだ本が10冊の生徒が必ずいるとわかります。
1組は,第3四分位数となる7冊。最大値となる11冊の生徒がいることはわかりますが,
8~10冊については,この箱ひげ図からは判断できません。
大問2
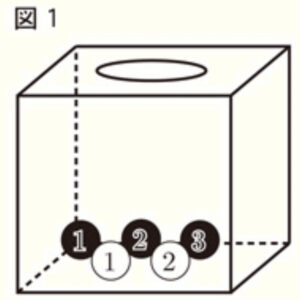
図1のように,箱の中に 1,2,3 の数字が1つずつ書かれた3個の赤玉と,1,2 の数字が1つずつ書かれた2個の白玉が入っている。
このとき,次の (1) ,(2) に答えなさい。
(1) 箱から玉を2個同時に取り出すとき,玉に書かれた数の和が4になる玉の取り出し方は,全部で何通りあるか,求めなさい。
【解説】
樹形図を書いてみると,3通りになるとわかります。

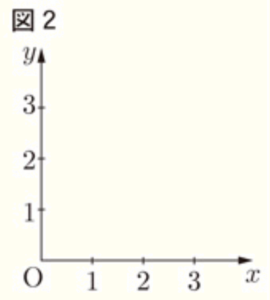
(2) 図2のように,座標軸と原点 \( O \) がある。
箱から玉を1個ずつ,もとにもどさずに続けて2回取り出す。1回目に取り出した玉の色と数字によって,点 \( P \) を の中の規則にしたがって座標軸上にとる。また,2回目に取り出した玉の色と数字によって,点 \( Q \) を の中の規則にしたがって座標軸上にとる。
<規則>
・赤玉を取り出したときは,玉に書かれた数を \( x \) 座標として \( x \) 軸上に点をとる。
・白玉を取り出したときは,玉に書かれた数を \( y \) 座標として \( y \) 軸上に点をとる。
このとき,\( O,P,Q \) を線分で結んだ図形が三角形になる確率を求めなさい。また,その考え方を説明しなさい。説明においては,図や表,式などを用いてよい。ただし,どの玉が取り出されることも同様に確からしいとする。
【解説】
\( O,P,Q \) を線分で結んだ図形が三角形にならない場合を考えると,
\( P,Q \) がどちらも \( x \) 軸上にあるとき,または, \( y \) 軸上にあるときです。
これは,2回とも同じ色の玉を取り出したときに成立します。
つまり,\( O,P,Q \) を線分で結んだ図形が三角形になるのは,
2回で異なる色の玉を取り出したときになります。
樹形図を書いてみると,すべての場合の数は20通り,異なる色になるのは12通りなので,
求める確率は \( \dfrac{12}{20}=\dfrac{3}{5} \)
大問3
図1のように,針金の3か所を直角に折り曲げて長方形の枠を作る。その長方形の周の長さを \( x \; cm \) とし,面積を \( y \; cm^2 \) とする。ただし,針金の太さは考えないものとする。
このとき,次の (1)~(3) に答えなさい。

(1) \( x=22 \) とする。横が縦より \( 3 \; cm \) 長い長方形となるとき,縦の長さを求めなさい。
【解説】
縦の長さを \( t \; cm \) とすると,横の長さは \( t+3 \; cm \) と表すことができます。
このとき,長方形の周の長さは \( 2 \times \{t+(t+3)\} \; cm \) と表すことができるので,
\( 2 \times \{t+(t+3)\}=22 \)
\( 2(2t+3)=22 \)
\( 2t+3=11 \)
\( t=4 \; (cm) \)
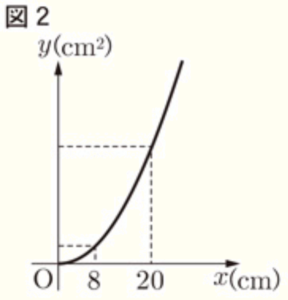
(2) 図2は,針金を折り曲げて正方形の枠を作るときの \( x \) と \( y \) の関係をグラフに表したものである。このグラフで表された関数について,\( x \) の値が8から20まで増加するときの変化の割合を求めなさい。
【解説】
\( x=8 \) のとき,縦と横の長さの和は \( 4 \; cm \) になるので,
正方形の1辺の長さは \( 2 \; cm \) で,\( y=4 \)
\( x=20 \) のとき,縦と横の長さの和は \( 10 \; cm \) になるので,
正方形の1辺の長さは \( 5 \; cm \) で,\( y=25 \)
変化の割合 \( =\dfrac{yの増加量}{xの増加量} \) なので,
変化の割合 \( =\dfrac{25-4}{20-8} \)
\( =\dfrac{21}{12} \)
\( =\dfrac{7}{4} \)
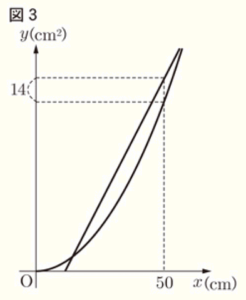
(3) 2つの針金をそれぞれ折り曲げて,縦と横の長さの比が 1:4 の長方形の枠と,縦が \( a \; cm \) で,横が縦より長い長方形の枠を作る。
図3は,この2通りの方法でできる長方形それぞれについて,\( x \) と \( y \) の関係をグラフに表したものである。これらのグラフから,2通りの方法でできるそれぞれの長方形の周の長さがともに \( 50 \; cm \) であるとき,面積の差が \( 14 \; cm^2 \) であることが読みとれる。
このとき,\( a \) の値を求めなさい。ただし,\( a<25/2 \) とする。なお,途中の計算も書くこと。
【解答&解説】
まず,縦と横の長さの比が 1:4 の長方形において,
縦の長さを \( t \; cm \) とすると,横の長さは \( 4t \; cm \)。
周の長さが \( 50 \; cm \) のとき,縦と横の長さの和は \( 25 \; cm \) なので,
\( t+4t=25 \)
\( 5t=25 \)
\( t=5 \)
よって,縦 \( 5 \; cm \),横 \( 20 \; cm \) なので,面積は,\( 5 \times 20=100 \; (cm^2) \)
このとき,縦が \( a \; cm \) の長方形の面積は,\( 100+14=114 \; (cm^2) \)
縦が \( a \; cm \) のとき,横の長さは,\( (25-a) \; cm \) と表すことができるので,
\( a(25-a)=114 \)
\( a^2-25a+114=0 \)
\( (a-6)(a-19)=0 \)
\( a=6,19 \)
\( a<25/2 \) より,\( a=6 \)
大問4
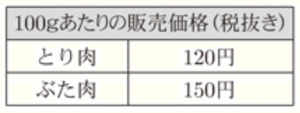
ある店では,とり肉とぶた肉をそれぞれパック詰めして販売している。右の表は,この店で販売しているとり肉,ぶた肉それぞれ100gあたりの価格を示したものである。
太郎さんは,この店でとり肉1パックと,ぶた肉2パックを購入した。太郎さんが購入したぶた肉2パックの内容量は等しく,とり肉とぶた肉の内容量はあわせて720g,合計金額は1020円であった。
このとき,太郎さんが購入したとり肉1パックとぶた肉1パックの内容量はそれぞれ何gか,方程式をつくって求めなさい。なお,途中の計算も書くこと。ただし,消費税は考えないものとする。
【解答&解説】
とり肉1パックの内容量を \( x \; g \) とぶた肉1パックの内容量を \( y \; g \) とすると,
とり肉とぶた肉の内容量の関係を表す方程式は,\( x+2y=720 \)
金額の関係を表す方程式は,\( \dfrac{x}{100} \times 120+\dfrac{y}{100} \times 150 \times 2=1020 \)
\( \left\{
\begin{array}{}
x+2y=720 \; ・・・ ① \; \\
\dfrac{x}{100} \times 120+\dfrac{y}{100} \times 150 \times 2=1020 \; ・・・ ➁\; \\
\end{array}
\right. \)
➁より
\( 2x+5y=1700 \) ・・・ ➁’
①\( \times 2 \)
\( 2x+4y=1440 \) ・・・ ①’
➁’\( – \)①’
\( y=260 \)
①に代入すると
\( x+520=720 \)
\( x=200 \)
よって,とり肉が200g,ぶた肉が260g
大問5
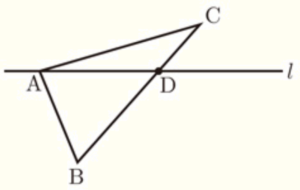
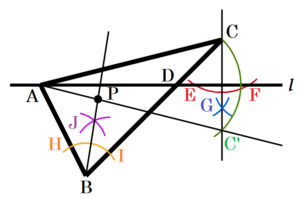
右の図のように,\( △ABC \) と,点 \( A \) を通る直線 \( l \) がある。また,辺 \( BC \) と直線 \( l \) の交点を \( D \) とする。これを用いて,次の の中の条件 ①~③ をすべて満たす点 \( P \) を作図しなさい。ただし,作図に用いた線は消さないこと。
➀ 点 \( P \) は,直線 \( l \) に対して点 \( B \) と同じ側にある。
➁ \( ∠ABP=∠CBP \)
➂ \( ∠DAP=∠DAC \)
【解答&解説】
➁より,点 \( P \) は \( ∠ABC \) の二等分線上にあります。
また,➂より,直線 \( l \) は \( ∠CAP \) の二等分線になります。
なので,直線 \( l \) を対象の軸として点 \( C’ \) を描いたとき,
直線 \( AC’ \) と \( ∠ABC \) の二等分線の交点が作図する点 \( P \) になります。
手順1 点 \( C \) を中心に弧を描く
(交点を \( E,F \) とします)
手順2 点 \( E,F \) を中心に同じ半径の弧を描く
(交点を \( G \) とします)
手順3 点 \( C,G \) を通る直線を描く
手順4 点 \( D \) を中心に線分 \( CD \) を半径とする
弧を描く
(手順3の直線との交点を \( C’ \) とします)
手順5 点 \( A,C’ \) を通る直線を描く
手順6 点 \( B \) を中心に弧を描く
(線分 \( AB,BC \) との交点を \( H,I \) とします)
手順7 点 \( H,I \) を中心に同じ半径の弧を描く
(交点を \( J \) とします)
手順8 点 \( B,J \) を通る直線を描く
以上で,手順5と手順8の直線の交点が作図する点 \( P \) になります。
大問6
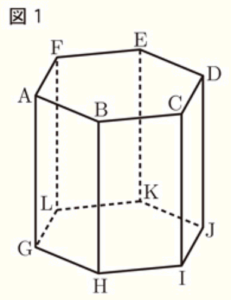
図1~図3のように,底面 \( GHIJKL \) が1辺 \( 4cm \) の正六角形で,\( AG=8cm \) の正六角柱 \( ABCDEF-GHIJKL \) がある。
このとき,次の (1)~(3) に答えなさい。
(1) 図1において,辺 \( AF \) に平行な辺をすべて書きなさい。
【解答&解説】
辺 \( CD \),辺 \( IJ \),辺 \( GL \)
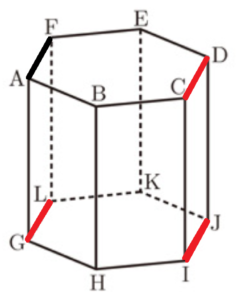
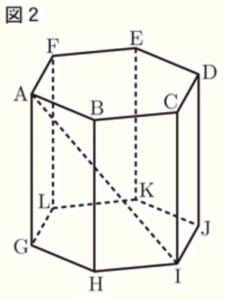
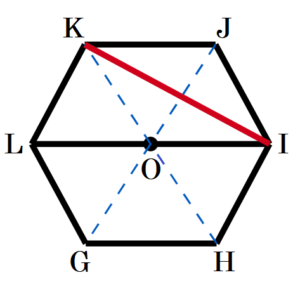
(2) 図2において,線分 \( AI \) の長さを求めなさい。なお,途中の計算も書くこと。
【解答】
点 \( H \) から線分 \( GI \) に垂線を引き,交点を点 \( P \) とすると,
\( △GHP \) において,\( GH:GP=2: \sqrt{3} \) なので,
\( GP=\dfrac{\sqrt{3}}{2}GH=\dfrac{\sqrt{3}}{2} \times 4=2\sqrt{3} \; (cm) \)
\( GI=2GP=4\sqrt{3} \; (cm) \)
\( △AGI \) において,三平方の定理より,
\( AI^2=AG^2+GI^2=8^2+(4\sqrt{3})^2=112 \)
\( AI=4\sqrt{7} \; (cm) \) (\(AI>0\)より)
【解説】
\( △GHP \)≡\( △IHP \), 正六角形の1つの内角は \( 120° \) なので,
\( △GHP \) は, \( 30°,60°,90° \) の直角三角形です。
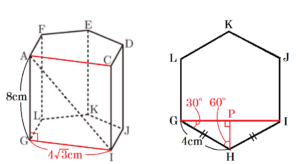
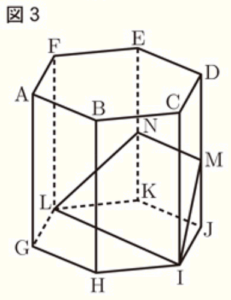
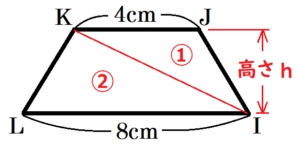
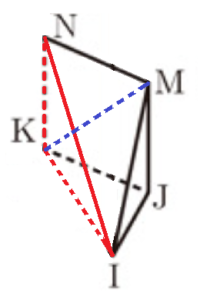
(3) 図3のように,辺 \( DJ \) 上に点 \( M \) を,辺 \( EK \) 上に点 \( N \) を,\( DE // MN \) となるようにとる。立体 \( MN-IJKL \) の体積が正六角柱 \( ABCDEF-GHIJKL \) の体積の \( \dfrac{1}{12} \) 倍になるとき,\( DM:MJ \) を最も簡単な整数の比で表しなさい。なお,途中の計算も書くこと。
【解答】
立体 \( MN-IJKL \) を面 \( NIK \) と面 \( MIK \) で切断すると,
三角すい \( N-IKL \) ,三角すい \( M-IJK \) ,三角すい \( I-MNK \) の3つの立体に分けられる。
3つの立体の体積比は,
三角すい \( N-IKL : \) 三角すい \( M-IJK : \) 三角すい \( I-MNK=2:1:1 \)
なので,
立体 \( MN-IJKL=4 \) 三角すい \( M-IJK \) ・・・ ①
\( MJ=x \; cm \) とすると,三角すい \( M-IJK \) の体積は
\( 4 \times 2\sqrt{3} \times \dfrac{1}{2} \times x \times \dfrac{1}{3}=\dfrac{4\sqrt{3}}{3}x \; (cm^3) \)
①より,立体 \( MN-IJKL \) の体積は
\( 4 \times \dfrac{4\sqrt{3}}{3}x=\dfrac{16\sqrt{3}}{3}x \; (cm^3) \)
正六角柱 \( ABCDEF-GHIJKL \) の体積は,底面 \( GHIJKL \) の面積が \( △IJK \) の6倍なので,
\( 4 \times 2\sqrt{3} \times \dfrac{1}{2} \times 6 \times 8=192\sqrt{3} \; (cm^3) \)
立体 \( MN-IJKL \) の体積が正六角柱 \( ABCDEF-GHIJKL \) の体積の \( \dfrac{1}{12} \) 倍になるとき,
\( \dfrac{16\sqrt{3}}{3}x=\dfrac{1}{12} \times 192\sqrt{3} \)
\( 64\sqrt{3}x=192\sqrt{3} \; (cm) \)
\( x=3 \)
より,\( MJ=3 \; cm \)
このとき,\( DM=8-3=5 \; (cm) \)
よって,\( DM:MJ=5:3 \)
【解説】
● 立体 \( MN-IJKL \) を面 \( NIK \) と面 \( MIK \) で切断する
まず,立体 \( MN-IJKL \) を面 \( NIK \) で切断すると,
三角すい \( N-IKL \) と四角すい \( I-MNKJ \) に分けられます。
さらに,四角すい \( I-MNKJ \) を面 \( MIK \) で切断すると,
三角すい \( N-IKL \) と三角すい \( M-IJK \) に分けられます。
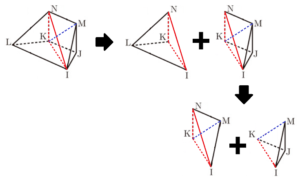
● 三角すい \( N-IKL \) と三角すい \( M-IJK \) の底面積の比
三角すい \( N-IKL \) の底面を \( △IKL \) ,
三角すい \( M-IJK \) の底面を \( △IJK \) と考えると,
底辺の長さが2倍で,高さは共通なので,
\( △IKL=IL \times h \times \dfrac{1}{2}=4h \)
\( △IJK=JK \times h \times \dfrac{1}{2}=2h \)
底面積の比は \( △IKL:△IJK=4h:2h=2:1 \)
● 三角すい \( M-IJK \) ,三角すい \( I-MNK \) の底面積の比
三角すい \( M-IJK \) の底面を \( △MJK \) ,
三角すい \( I-MNK \) の底面を \( △MNK \) と考えると,
面\( MNKJ \) は長方形で,線分 \( MK \) は対角線にあたります。
長方形の面積は,対角線によって二等分されるので,\( △MJK=△MNK \)
● 底面 \( GHIJKL \) の面積が \( △IJK \) の6倍
底面 \( GHIJKL \) は正六角形なので,\( JK//IL \) です。
底面 \( GHIJKL \) の対角線の交点を点 \( O \) とすると,
等積変形より,\( △OJK=△IJK \) 。
よって,底面 \( GHIJKL=6△OJK=6△IJK \)
大問7
図1~図3のように,円 \( O \) の周上に4点 \( A,B,C,D \) があり,線分 \( AC \) と \( BD \) の交点を \( E \) とする。
このとき,次の (1)~(3) に答えなさい。
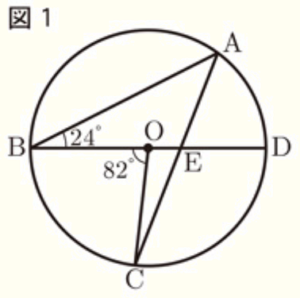
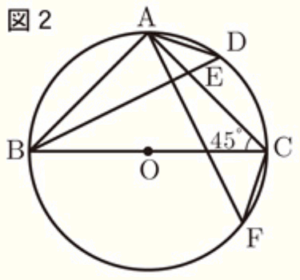
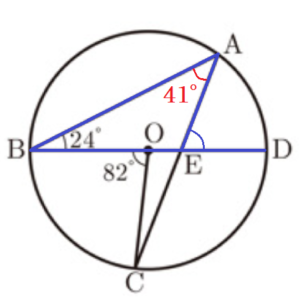
(1) 図1のように,\( BD \) は円 \( O \) の直径,\( ∠ABD=24°,∠BOC=82° \) のとき,\( ∠AED \) の大きさを求めなさい。
【解説】
\( ∠BAC \) は弧 \(BC\) の円周角なので,
\( ∠BAC=\dfrac{1}{2}∠BOC=41° \)
\( ∠AED \) は \( △ABE \) の外角なので,
\( ∠AED=∠ABE+∠BAE=24°+41°=65° \)
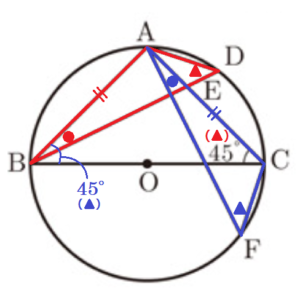
(2) 図2のように,\( BC \) は円 \( O \) の直径,\( ∠ACB=45° \) とする。また,点 \( A \) を含まない弧 \( BC \) 上に点 \( F \) を,弧 \( AD= \) 弧 \( CF \) となるようにとる。
このとき,\( △ABD≡△CAF \) であることを証明しなさい。
【解答】
\( △ABD \) と \( △CAF \) において,
弧 \( AD= \) 弧 \( CF \) より,\( ∠ABD=∠CAF \) ・・・ ①
直径 \( BC \) に対する円周角なので,\( ∠BAC=90° \) ・・・ ➁
\( ∠BAC=90°,∠ACB=45° \) より,
\( ∠ABC=180°-(∠BAC+∠ACB)=45° \) なので,
\( ∠ABC=∠ACB=45° \) ・・・ ➂
➁➂より,\( △ABC \) は直角二等辺三角形なので,
\( AB=CA \) ・・・ ④
弧 \( AB \) に対する円周角なので,\( ∠ADB=∠ACB \) ・・・ ➄
弧 \( AC \) に対する円周角なので,\( ∠CFA=∠ABC \) ・・・ ⑥
➂➄⑥より,\( ∠CFA=∠ADB \) ・・・ ➆
\( ∠BAD=180°-(∠ABD+∠ADB) \),
\( ∠ACF=180°-(∠CAF+∠CFA) \) なので,
①➆より,\( ∠BAD=∠ACF \) ・・・ ⑧
①④⑧より,1組の辺の長さとその両端の角の大きさが等しいので,
\( △ABD≡△CAF \)
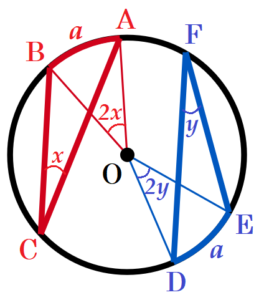
【解説】
● 弧の長さが等しいとき,円周角も等しい
\( ∠ACB=x,∠DFE=y \) ,円周の長さを \( l \),
弧\( AB= \)弧\( DE=a \) とすると,
中心角 \( ∠AOB=2x,∠DOE=2y \) となります。
中心角 \( ∠AOB,∠DOE \) は,
\( ∠AOB=360 \times \dfrac{a}{l}=\dfrac{360a}{l} \)
\( ∠DOE=360 \times \dfrac{a}{l}=\dfrac{360a}{l} \)
と表すことができるので,
\( 2x=\dfrac{360a}{l} \)
\( 2y=\dfrac{360a}{l} \)
よって,\( x=y \)
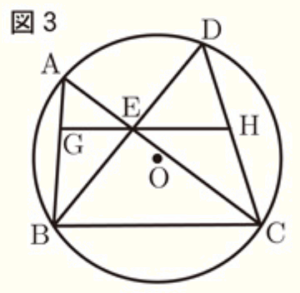
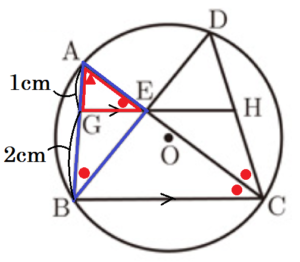
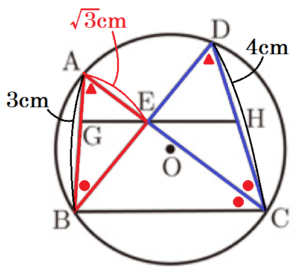
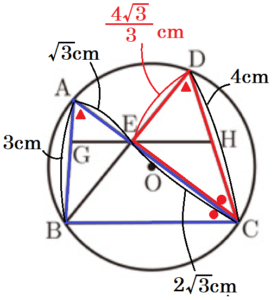
(3) 図3において, \( AC \) は \( ∠BCD \) の二等分線である。
また,点 \( G \) を線分 \( AB \) 上に \( GE // BC \) となるようにとり,直線 \( GE \) と線分 \( CD \) の交点を \( H \) とする。
\( AG=1 cm,GB=2 cm,CD=4cm \) のとき,線分 \( BC \) の長さを求めなさい。なお,途中の計算も書くこと。
【解答】
\( △AGE \) ∽ \( △AEB \) より,
\( AG:AE=AE:AB \)
\( 1:AE=AE:3 \)
\( AE=\sqrt{3} \; (cm) \) (\( AE>0 \) より)
\( △AGE \) ∽ \( △ABC \),\( AG=1 cm,GB=2 cm \) より,
\( AG:GB=AE:EC \)
\( 1:2= \sqrt{3}:EC \)
\( EC=2\sqrt{3} \; (cm) \)
\( △AEB \) ∽ \( △DEC \),\( AB=3 cm,CD=4 cm \) より,
\( AB:DC=AE:DE \)
\( 3:4= \sqrt{3}:DE \)
\( DE=\dfrac{4\sqrt{3}}{3} \; (cm) \)
\( △ABC \) ∽ \( △DEC \),\( AB=3 cm,DE=\dfrac{4\sqrt{3}}{3} cm \) より,
\( AB:DE=BC:EC \)
\( 3:\dfrac{4\sqrt{3}}{3}=BC:2\sqrt{3} \)
\( \dfrac{4\sqrt{3}}{3}BC=6\sqrt{3} \)
\( 4\sqrt{3}BC=18\sqrt{3} \)
\( BC=\dfrac{9}{2} \; (cm) \)