大問1
(1) 次のア~オの計算をしなさい。
ア \( -4-7 \)
イ \( 5+(-3^2) \times 2 \)
【解説】
\( =5+(-9) \times 2 \)
\( =5+(-18) \)
\( =-13 \)
ウ \( 4ab^3 \div \dfrac{10}{7}ab^2 \)
【解答】
\( \dfrac{14}{5}b \)
【解説】
\( =\dfrac{4ab^3 \times 7}{10ab^2} \)
\( =\dfrac{14}{5}b \)
エ \( \dfrac{x-3y}{2}-\dfrac{x-5y}{8} \)
【解答】
\( \dfrac{3x-7y}{8} \)
【解説】
\( =\dfrac{8(x-3y)-2(x-5y)}{16} \)
\( =\dfrac{8x-24y-2x+10y}{16} \)
\( =\dfrac{6x-14y}{16} \)
\( =\dfrac{3x-7y}{8} \)
オ \( \sqrt{96} \times \dfrac{1}{\sqrt{2}}+\sqrt{27} \)
【解説】
\( =\sqrt{48}+3\sqrt{3} \)
\( =4\sqrt{3}+3\sqrt{3} \)
\( =7\sqrt{3} \)
(2) 次の方程式を解きなさい。
\( 3x^2-5x+1=0 \)
【解答】
\( x=\dfrac{5±\sqrt{13}}{6} \)
【解説】
この方程式を \( ax^2+bx+c=0 \) と考えると,\( a=3,b=-5,c=1 \) なので,
解の公式より,
\( x=\dfrac{-(-5)±\sqrt{(-5)^2-4 \times 3 \times 1}}{2 \times 3} \)
\( =\dfrac{5±\sqrt{13}}{6} \)
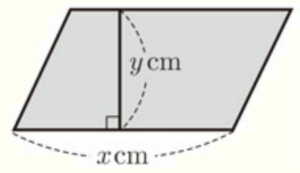
(3) 右の図のように,面積が \( 10 \; cm^2 \) の平行四辺形の底辺を \( x \; cm \),高さを \( y \; cm \) とする。このとき,\( y \) を \( x \) の式で表しなさい。
【解答】
\( y=\dfrac{10}{x} \)
【解説】
平行四辺形の面積を求める公式より,\( xy=10 \) なので,
これを \( y \) について解くと,
\( y=\dfrac{10}{x} \)
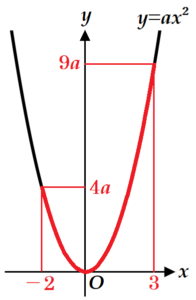
(4) 関数 \( y=ax^2 \) について,\( x \) の変域が \( -2≦x≦3 \) のとき,\( y \) の変域が \( 0≦y≦15 \) である。このとき,\( a \) の値を求めなさい。
【解答】
\( a=\dfrac{5}{3} \)
【解説】
関数 \( y=ax^2 \) において,\( x \) の変域が \( 0 \) を含んでいるとき,
\( a>0 \) であれば,\( y \) の最小値が \( 0 \),
\( a<0 \) であれば,\( y \) の最大値が \( 0 \)
になります。
ここから,\( a>0 \) であるとわかります。
\( a>0 \) の場合,
\( x \) の絶対値が最大になるときに \( y \) は最大値をとります。
\( -2≦x≦3 \) のうち,絶対値が最大になるのは
\( x=3 \) のときなので,このときの \( y \) の値は,
\( y=a \times 3^2=9a \)
であり,これが最大値 \( 15 \) になるので,
\( 9a=15 \)
\( a=\dfrac{5}{3} \)
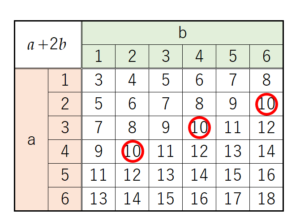
(5) 1から6までの目が出る大小2つのさいころを同時に1回投げて,大きいさいころの出た目の数を \( a \),小さいさいころの出た目の数を \( b \) とする。このとき,\( a+2b=10 \) となる確率を求めなさい。ただし,2つのさいころはともに,どの目が出ることも同様に確からしいとする。
【解説】
\( a \) と \( b \) の組み合わせと,それぞれの組み合わせにおける \( a+2b \) の値を表に書き出すと,
\( a+2b=10 \) となる組み合わせは3通り,すべての組み合わせは36通りなので,
求める確率は \( \dfrac{3}{36}=\dfrac{1}{12} \)
大問2
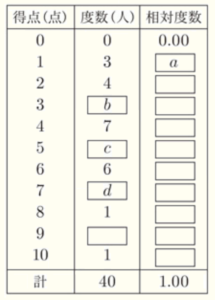
A中学校の3年1組の生徒 \( 40 \) 人に,\( 10 \) 点満点のテストを実施した。右の表は,テストの得点について,度数および相対度数をまとめたものである。このとき,次の(1),(2)に答えなさい。
(1) 表の \( \fbox{ a } \) にあてはまる数を求めなさい。ただし,小数第3位を四捨五入して,小数第2位まで求めること。
【解説】
相対度数は,「求める階級の度数」 \( \div \) 「すべての階級の度数の合計」で求めることができるので,
\( 3 \div 40=0.075 \)
\( 0.075 \) の小数第3位を四捨五入すると,\( 0.08 \)
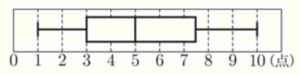
(2) 右の図は,テストの得点の分布のようすを箱ひげ図に表したものである。
このとき,表の \( \fbox{ b },\fbox{ c },\fbox{ d } \) にあてはまる数の組み合わせとして適当でないものを,次のア~エから1つ選び,その符号を書きなさい。また,そう判断した理由を,この箱ひげ図をもとに説明しなさい。 説明においては,図や表,式などを用いてよい。
ア \( b=5 \;\; c=4 \;\; d=1 \) イ \( b=5 \;\; c=2 \;\; d=3 \)
ウ \( b=4 \;\; c=4 \;\; d=3 \) エ \( b=4 \;\; c=3 \;\; d=3 \)
【解答】
ウ
【理由】
箱ひげ図より第三四分位数は \( 7.5 \) 点なので,\( 8 \) 点の人がいることを踏まえると,
得点の低い方から30番目の人の得点は \( 7 \) 点,31番目の人の得点は \( 8 \) 点である。
ここから,得点が \( 9 \) 点の人の人数は,\( 8 \) 人であり,全体で \( 40 \) 人であることから,
\( b+c+d \) の値は
\( 0+3+4+b+7+c+6+d+1+8+1=40 \)
\( b+c+d=10 \)
ウは,\( b+c+d=4+4+3=11 \) になるので,適当ではないといえる。
【解説】
すべての階級の度数の合計が \( 40 \) 人であることから,
第一四分位数は得点の低い方から10番目と11番目の人の得点の平均値,
中央値は得点の低い方から20番目と21番目の人の得点の平均値,
第三四分位数は得点の低い方から30番目と31番目の人の得点の平均値,
になります。
箱ひげ図より,第三四分位数は \( 7.5 \) 点なので,
得点の低い方から30番目(得点の高い方から11番目)の人の得点は \( 7 \) 点,
得点の低い方から31番目(得点の高い方から10番目)の人の得点は \( 8 \) 点
なので,得点が \( 9 \) 点の人の人数は,\( 10-(1+1)=8 \) 人となります。
このとき,度数に注目すると,
\( 0+3+4+b+7+c+6+d+1+8+1=40 \)
\( b+c+d=10 \)
ウは,\( b+c+d=4+4+3=11 \) になるので,適当ではないといえる。
大問3
Aさんは,登山口から山頂までの道のりが \( 1200 \; m \) である山に登った。午前 \( 9 \) 時に登山口を出発し,山頂まで一定の速さで歩いて登った。山頂で \( 20 \) 分間休んだ後,一定の速さで歩いて下山し,登山口に戻った。
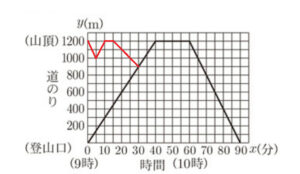
次の図は,Aさんが移動するようすについて,Aさんが登山口を出発してから \( x \) 分後に,登山口からの道のりが \( y \; m \) の地点にいるとして,\( x \) と \( y \) の関係をグラフに表したものである。
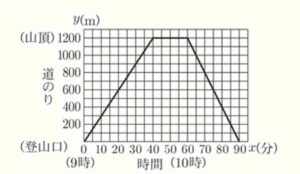
このとき,次の(1)~(3)に答えなさい。なお,登山口は1つしかなく,登山口と山頂を結ぶ道も1本しかないものとする。
(1) 図のグラフより,Aさんが山頂から歩いて下山し,登山口に戻るまでにかかった時間は何分間か,求めなさい。
【解説】
グラフより,下山を開始したのは,登山口を出発してから \( 60 \) 分後,
登山口に戻ってきたのは,登山口を出発してから \( 90 \) 分後なので,
下山にかかった時間は \( 30 \) 分間。
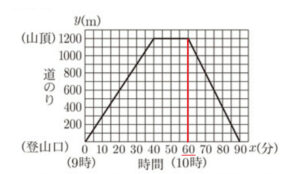
(2) Aさんが登山口を出発した午前 \( 9 \) 時に,Bさんは山頂から分速 \( 40 \; m \) で歩いて下山を開始したが,\( 200 \; m \) 歩いたところで忘れ物に気づき,同じ速さで山頂に引き返した。山頂で忘れ物を探し,見つけた後,分速 \( 20 \; m \) で歩いて再び下山を開始した。 その後,登ってきたAさんと午前 \( 9 \) 時 \( 30 \) 分にすれちがった。
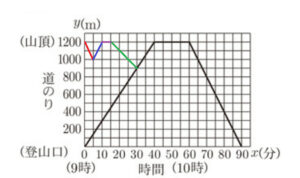
Bさんが最初に下山を開始してから \( x \) 分後に,登山口からの道のりが y \; m の地点にいるとする。午前 \( 9 \) 時から午前 \( 9 \) 時 \( 30 \) 分までのBさんが移動するようすについて,\( x \) と \( y \) の関係を表すグラフを図にかき入れ,Bさんが山頂に戻ってから再び下山を開始するまでの時間は何分間か,求めなさい。
【解答】
\( 5 \) 分間
【解説】
Bさんは山頂から分速 \( 40 \; m \) で歩いたので,\( 200 \; m \) 歩くのにかかった時間は
\( 200 \div 40=5 \)(分)
これをグラフに書き込むと,赤の直線になります。
そこから,同じ速さで山頂に戻ったので,\( 5 \) 分かけて山頂まで戻ることになり,
これをグラフに書き込むと,青の直線になります。
その後,再び下山を開始してからは,分速 \( 20 \; m \) で歩いたので,
これを表す直線は \( x \) 方向に1マス進むごとに \( y \) 方向に-1マス進む右下がりの直線になります。
AさんとBさんは午前 \( 9 \) 時 \( 30 \) 分にすれちがったので,
\( x=30 \) のところの黒の直線 \( (x,y)=(30,900) \) が終点になるように右下がりの直線を書くと,
緑の直線になります。
このとき,青の直線の終点と緑の直線の始点をつないだ紫の直線が
山頂で忘れ物を探していた時間を表していることになります。
よって,忘れ物を探していた時間は \( 5 \) 分間。
(3) Cさんは,Aさんより後に登山口を出発して,Aさんが山頂まで登ったときと同じ速さで歩き,Aさんが下山を開始した午前 \( 10 \) 時に登山口からの道のりが \( 400 \; m \) の地点にいた。Cさんが登山口を出発したのは,Aさんが登山口を出発してから何分何秒後か,求めなさい。なお,途中の計算も書くこと。
【解答】
Aさんは,山頂まで登った速さは \( 1200 \div 40=30 \) で,分速 \( 30 \; m \) 。
グラフで,Cさんが歩いた状態を表す直線の式を \( y=30x+b \) とすると,
この直線は \( (60,400) \) を通るので,
\( 400=30 \times 60+b \)
\( b=-1400 \)
よって,この直線の式は \( y=30x-1400 \) と表すことができる。
\( y=0 \) を代入すると,
\( 0=30x-1400 \)
\( x=\dfrac{140}{3}=46\dfrac{2}{3} \)(分)
\( \dfrac{2}{3} \) 分を秒に換算すると,
\( \dfrac{2}{3} \times 60=40 \)(秒)
以上より,求める時間は,\( 46 \) 分 \( 40 \) 秒後
大問4
あるバスケットボールの試合において,Aチームは \( 3 \) 点シュート,\( 2 \) 点シュート,\( 1 \) 点のフリースローの合計得点が \( 68 \) 点であり,そのうち \( 1 \) 点のフリースローによる得点は \( 8 \) 点であった。Aチームはこの試合で,\( 3 \) 点シュート,\( 2 \) 点シュート,\( 1 \) 点のフリースロー合わせて \( 80 \) 本のシュートをして,そのうち \( 45 \; \% \) のシュートを決めた。
Aチームがこの試合で決めた \( 3 \) 点シュートと \( 2 \) 点シュートはそれぞれ何本か,方程式をつくって求めなさい。 なお,途中の計算も書くこと。
【解答】
Aチームがこの試合で決めた \( 3 \) 点シュートの本数を \( x \) 本,\( 2 \) 点シュートの本数を \( y \) 本 とすると,
\( \left\{ \begin{array}{}
3x+2y+8=68 \;\; ・・・ \;\; ➀ \\
x+y+8=80 \times \dfrac{45}{100} \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀より,
\( 3x+2y=60 \) ・・・ ➀’
➁より,
\( x+y=28 \) ・・・ ➁’
➀’\( – \)➁’\( \times 2 \)
\( x=4 \)
➁’に代入すると,
\( 4+y=28 \)
\( y=24 \)
よって,Aチームがこの試合で決めた
\( 3 \) 点シュートの本数は,\( 4 \) 本
\( 2 \) 点シュートの本数は,\( 24 \) 本
大問5
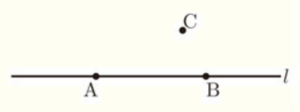
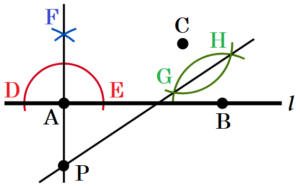
右図のように,2点 \( A,B \) を通る直線 \( l \) と,\( l \) 上にない点 \( C \) がある。
これを用いて,次の の中の条件①,②をともに満たす点 \( P \) を作図しなさい。ただし,作図に用いた線は消さないこと。
➀ \( PA⊥l \)
② 点 \( P \) は,2点 \( B,C \) を通る円の中心である。
【解答】
手順1 点 \( A \) を中心に円弧を描く。
(直線 \( l \) との交点を \( D,E \) とします。)
手順2 点 \( D,E \) を中心に円弧を描く。
(交点を \( F \) とします。)
手順3 2点 \( A,F \) を通る直線を描く。
手順4 点 \( B,C \) を中心に円弧を描く。
(交点を \( G,H \) とします。)
手順5 2点 \( G,H \) を通る直線を描く。
手順3と手順5の直線の交点が求める点 \( P \) になります。
【解答】
円の中心は必ず任意の弦の垂直二等分線上にあるので,
2点 \( B,C \) を通る円の中心は,弦 \( BC \) の垂直二等分線上にあることになります。
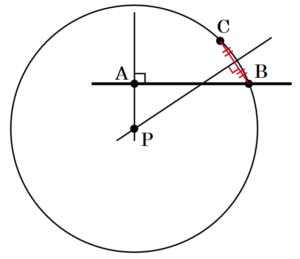
円の中心は必ず任意の弦の垂直二等分線上にあるといえる理由
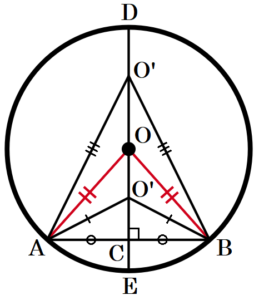
2点 \( A,B \) を通る円の中心を点 \( O \),弦 \( AB \) とその垂直二等分線との交点を点 \( C \),
垂直二等分線と円 \( O \) の交点を \( D,E \),線分 \( DE \) 上の任意の点を点 \( O’ \) とすると,
\( △O’AC \) と \( △O’BC \) において,
\( AC=BC \) ・・・ ➀
\( ∠O’CA=∠O’CB=90° \) ・・・ ➁
\( O’C \) は共通 ・・・ ➂
➀➁③より,
2組の辺とその間の角がそれぞれ等しいので,
\( △O’AC≡△O’BC \)
対応する辺は等しいので,\( O’A=O’B \)
つまり,点 \( O’ \) が線分 \( DE \) 上のどの位置に
あっても \( O’A=O’B \) になります。
中心 \( O \) について,半径なので,\( OA=OB \) であることから,
線分 \( DE \) の中点が中心 \( O \) になります。
よって,円の中心は必ず任意の弦の垂直二等分線上にあるといえます。
大問6
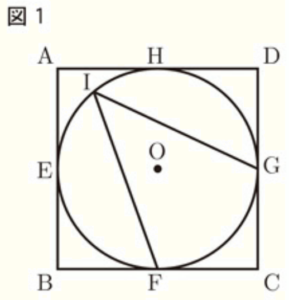
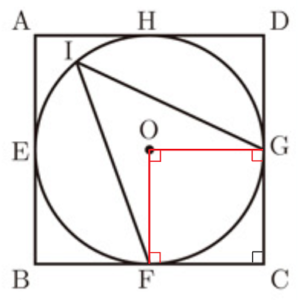
図1~図3のように,1辺の長さが \( 4 \; cm \) の正方形 \( ABCD \) に,円 \( O \) が4点 \( E,F,G,H \) で接している。
このとき,次の(1)~(3)に答えなさい。
(1) 図1のように,点 \( F \) を含まない 弧 \( EH \) 上に点 \( I \) をとる。このとき,\( ∠FIG \) の大きさを求めなさい。
【解説】
補助線 \( OF,OG \) をひくと,
\( OF⊥BC,OG⊥CD,∠BCD=90° \) なので,
四角形 \( OFCG \) において,
\( ∠FOG=360°-90° \times 3=90° \)
\( ∠FIG \) は,弧 \( FG \) の円周角,
\( ∠FOG \) は,弧 \( FG \) の中心角なので,
\( ∠FIG=\dfrac{1}{2} \times 90°=45° \)
(2) 図2のように,線分 \( AC \) と円 \( O \) との交点のうち,点 \( A \) に近い方を点 \( J \),もう一方を点 \( K \) とする。また,直線 \( DK \) と円 \( O \) との交点のうち点 \( K \) 以外の交点を \( L \),直線 \( DK \) と辺 \( BC \) の交点を \( M \),直線 \( JL \) と \( AD \) との交点を \( N \) とする。
このとき,\( △CDM \) ∽ \( △LND \) であることを証明しなさい。
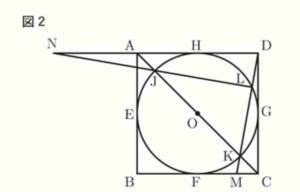
【解答】
\( △CDM \) と \( △LND \) において,
正方形の内角なので,\( ∠DCM=∠CDA=90° \) ・・・ ➀
直径に対する円周角なので,\( ∠JLK=90° \)
4点 \( D,L,K,M \) は一直線上にあるので,\( ∠NLD=180°- ∠JLK=90° \) ・・・ ➁
➀➁より,\( ∠DCM=∠NLD=90° \) ・・・ ➂
\( ∠DMC=180°-(∠CDM+∠DCM)=90°-∠CDM \) ・・・ ➃
\( ∠NDL=∠CDA-∠CDM=90°-∠CDM \) ・・・ ➄
➃➄より,\( ∠DMC=∠NDL \) ・・・ ⑥
➂➅より,2組の角がそれぞれ等しいので,
\( △CDM \) ∽ \( △LND \)
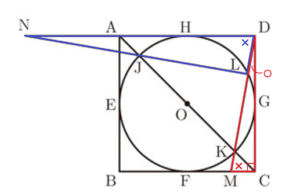
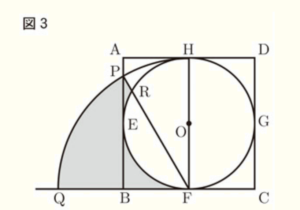
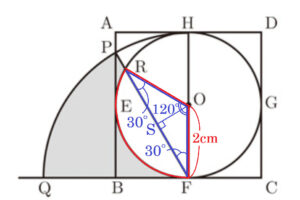
(3) 図3のように,点 \( F \) を中心として線分 \( FH \) を半径とする円 \( F \) と辺 \( AB \) との交点を \( P \),円 \( F \) と半直線 \( CB \) との交点を \( Q \) とする。また,線分 \( FP \) と円 \( O \) との交点のうち,点 \( F \) 以外の交点を \( R \) とする。
このとき,弧 \( PQ \),線分 \( QF \),弧 \( FR \),線分 \( RP \) で囲まれた 部分の面積を求めなさい。なお,途中の計算も書くこと。
【解答】
\( FP=4 \; cm,FB=\dfrac{1}{2}BC=2 \; cm,∠PBF=90° \) より,
\( △PBF \) は \( 30°,60°,90° \) の直角三角形なので,\( ∠BFP=60° \) なので,
おうぎ形 \( FPQ \) の面積は,
\( \pi{} \times 4^2 \times \dfrac{60}{360}=\dfrac{8}{3}\pi{} (cm^2) \)
\( △OFR \) は,\( OF=OR=2 \; cm,∠ORF=∠OFR=30° \) の二等辺三角形なので,
\( ∠ROF=180°-(30°+30°)=120° \)
点 \( O \) から線分 \( RF \) に垂線をひき,交点を \( S \) とすると,
\( OS=1 \; cm,FS=\sqrt{3} \; cm \) であり,
\( △OFS=1 \times \sqrt{3} \times \dfrac{1}{2}=\dfrac{\sqrt{3}}{2} \; (cm) \)
\( △OFR=2△OFS=\sqrt{3} \; (cm) \)
おうぎ形 \( OFR \) の面積は,
\( \pi{} \times 2^2 \times \dfrac{120}{360}=\dfrac{4}{3}\pi{} (cm^2) \)
以上より,求める面積は,
\( \dfrac{8}{3}\pi{}- \left(\dfrac{4}{3}\pi{}-\sqrt{3} \right)=\dfrac{4}{3}\pi{}+\sqrt{3} (cm^2) \)
【解説】
部分は,おうぎ形 \( FPQ \) から
の部分を取り除いた形になっています。
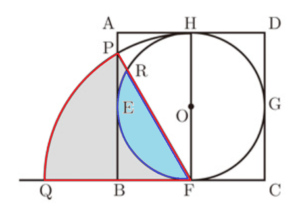
【おうぎ形 \( FPQ \) の中心角】
\( FH=CD=4 \; cm \) より,おうぎ形 \( FPQ \) は半径 \( 4 \; cm \) のおうぎ形であり,
\( FP=4 \; cm,FB=\dfrac{1}{2}BC=2 \; cm,∠PBF=90° \) より,
\( △PBF \) は \( 30°,60°,90° \) の直角三角形なので,中心角 \( BFP \) は,\( 60° \) になっています。
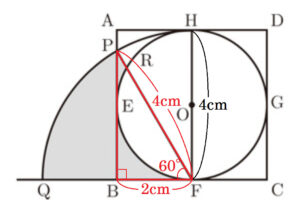
【 部分の面積】
部分は,おうぎ形 \( OFR \) から \( △OFR \) の部分を取り除いた形になっています。
\( ∠OFR=90°-∠BFP=30° \) であり,\( OR=OF \) より,\( ∠ORF=∠OFR=30° \) なので,
\( ∠ROF=180°-(30°+30°)=120° \)
\( △OFR \) において,点 \( O \) から線分 \( RF \) に垂線をひき,交点を \( S \) とすると,
\( △OFS \) と \( △ORS \) はどちらも斜辺が \( 2 \; cm \) で \( 30°,60°,90° \) の
直角三角形になっています。
大問7
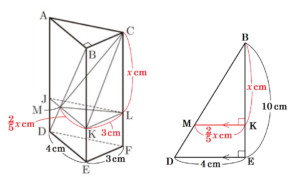
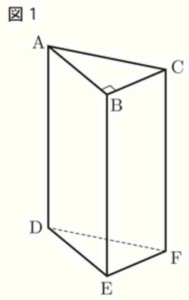
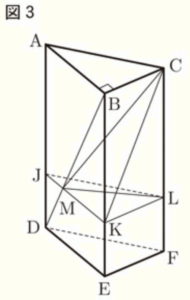
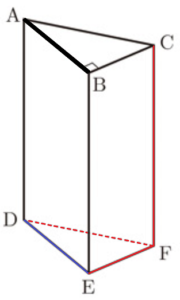
図1~図3のように,底面 \( ABC \) が \( AB=4 \; cm,BC=3 \; cm,AC=5 \; cm \) の直角三角形で,高さ \( AD=10 \; cm \) の三角柱 \( ABC-DEF \) がある。
このとき,次の(1)~(3)に答えなさい。
(1) 図1において,辺 \( AB \) とねじれの位置にある辺をすべて書きなさい。
【解答】
辺 \( CF \),辺 \( DF \),辺 \( EF \)
【解説】
ねじれの位置にある辺とは,どこまで行っても交わらない辺のうち,
平行ではない辺になります。
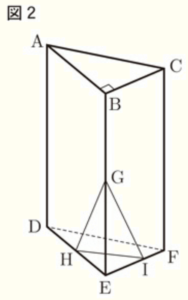
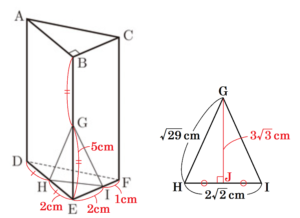
(2) 図2において,辺 \( BE,DE \) の中点をそれぞれ \( G,H \) とする。また,辺 \( EF \) 上に点 \( I \) を,\( EI=IF=2:1 \) となるようにとる。
このとき,\( △GHI \) の面積を求めなさい。 なお,途中の計算も書くこと。
【解答】
\( EH=EI=2 \; cm,EG=5 \; cm \) なので,
\( HI=\sqrt{2}EH=2\sqrt{2} \; (cm) \)
\( GH^2=5^2+2^2=29 \)
\( GH=\sqrt{29} \; (cm) \) (\( GH>0 \) より)
\( △GEH≡△GEI \) なので,\( GI=GH=\sqrt{29} \; (cm) \)
\( △GHI \) の高さを \( GJ \) とすると,
\( GJ^2=(\sqrt{29})^2-(\sqrt{2})^2=27 \)
\( GJ=3\sqrt{3} \; (cm) \) (\( GJ>0 \) より)
よって,\( △GHI \) の面積は,
\( 2\sqrt{2} \times 3\sqrt{3} \times \dfrac{1}{2}=3\sqrt{6} \; (cm^2) \)
(3) 図3において,辺 \( AD \) 上に点 \( J \) を,辺 \( BE \) 上に点 \( K \) を,辺 \( CF \) 上に点 \( L \) を,平面 \( JKL \) が平面 \( DEF \) と平行になるようにとる。線分 \( BD \) と \( JK \) の交点を \( M \) とするとき,三角錐 \( CKLM \) の体積が \( 10 \; cm^3 \) であった。
このとき,線分 \( CL \) の長さを求めなさい。なお,途中の計算も書くこと。
【解答】
\( CL=x \; cm \) とすると,\( BK=CL=x \; cm \) であり,
\( MK//DE \) より,\( △BMK \) ∽ \( △BDE \) なので,
\( MK:DE=BK:BE \)
\( MK:4=x:10 \)
\( MK=\dfrac{2}{5}x \; (cm) \)
三角錐 \( CKLM \) の体積が \( 10 \; cm^3 \) なので,
\( \left( \dfrac{2}{5}x \times 3 \times \dfrac{1}{2} \right) \times x \times \dfrac{1}{3}=10 \)
\( x^2=50 \)
\( x=5\sqrt{2} \; (cm) \)
よって,\( CL=5\sqrt{2} \; cm \)