大問1
(1) \( 2+(-4) \) を計算しなさい。
【解説】
\( =2-4 \)
\( =-2 \)
(2) \( 9 \times \dfrac{x-2}{3} \) を計算しなさい。
【解説】
\( =\dfrac{9(x-2)}{3} \)
\( =3(x-2) \)
\( =3x-6 \)
(3) \( 4\sqrt{3}-\sqrt{12} \) を計算しなさい。
【解説】
\( =4\sqrt{3}-2\sqrt{3} \)
\( =2\sqrt{3} \)
(4) \( x^2-3x-18 \) を因数分解しなさい。
(5) 2次方程式 \( (x-2)^2=5 \) を解きなさい。
【解説】
展開すると,
\( x^2-4x+4=5 \)
\( x^2-4x-1=0 \)
解の公式より,
\( x=\dfrac{-(-4)±\sqrt{(-4)^2-4 \times 1 \times (-1)}}{2 \times 1} \)
\( =\dfrac{4±\sqrt{16+4}}{2} \)
\( =\dfrac{4±2\sqrt{5}}{2} \)
\( =2±\sqrt{5} \)
【別解】
\( x-2=±\sqrt{5} \)
\( x=2±\sqrt{5} \)
大問2
連続する2つの奇数を,文字を用いた式で表します。\( n \) を整数とするとき,連続する2つの奇数をそれぞれ,\( n \) を用いた式で表しなさい。
【解説】
全ての整数は,「偶数,奇数,偶数,奇数,・・・ 」と偶数と奇数が順番に並んでいます。
偶数は「2で割り切れる数」のことをいうので,ある偶数を \( 2n \) と表すことができ,
このとき,奇数は \( 2n \) より1大きい数なので,\( 2n+1 \) と表すことができます。
また,その次の奇数はもとの奇数より2大きい数なので,
\( (2n+1)+2=2n+3 \) と表すことができます。

大問3
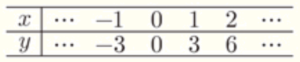
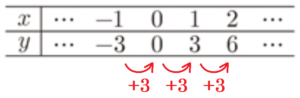
右の表は,\( y \) が \( x \) に比例するときの,\( x \) の値に対応する \( y \) の値を表しています。この比例の関係について,\( y \) を \( x \) の式で表しなさい。
【解説】
\( y \) が \( x \) に比例するとき,\( x \) と \( y \) の関係は,\( y=ax+b \) の形で表されます。
表から,\( x \) の値が \( 1 \) 増えるごとに \( y \) の値は \( 3 \) ずつ増えているので,
傾き \( a=3 \) になります。
また,表から,\( x=0 \) のとき,\( y=0 \) なので,
切片 \( b=0 \) になります。
よって,求める式は \( y=3x \) になります。
大問4
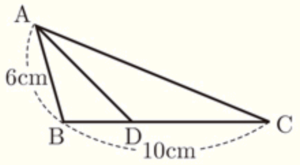
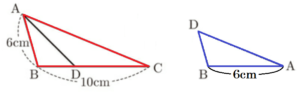
(1) 右の図で, \( △ABC \) ∽ \( △DBA \) のとき,\( BD \) の長さを求めなさい。
【解答】
\( BD=\dfrac{18}{5} \; cm \)
【解説】
相似な三角形の対応する辺の比は等しいので,
\( AB:DB=BC:BA \)
\( 6:DB=10:6 \)
\( 10DB=36 \)
\( DB=\dfrac{18}{5} \; (cm) \)
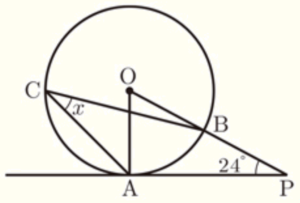
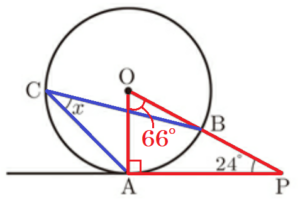
(2) 右の図で,3点 \( A,B,C \) が円 \( O \) の周上にあります。点 \( A \) を通る接線と直線 \( OB \) との交点を \( P \) とします。\( ∠OPA=24° \) のとき,∠x の大きさを求めなさい。
【解説】
円の半径と接線は接点において垂直に交わるので,
\( ∠OAP=90° \)
\( △OAP \) において,
\( ∠OAB=180°-(∠OAP+∠OPA) \)
\( =180°-(90°+24°) \)
\( =66° \)
\( ∠AOB \) は \( \stackrel{\huge\frown}{ AB } \) に対する中心角,\( ∠ACB \) は \( \stackrel{\huge\frown}{ AB } \) に対する円周角なので,
\( ∠x=\dfrac{1}{2}∠AOB=33° \)
(3) 次のア~エのことがらのうち,正しいものを一つ選び,その記号を書きなさい。
ア 台形は,ひし形である。
イ 長方形は,正方形である。
ウ ひし形は,平行四辺形である。
エ 平行四辺形は,長方形である。
【解説】
例えば,「Aという図形は,ひし形である」が成り立つとき,
Aという図形の性質はひし形の性質をすべて含んでいる必要があります。
ア ・・・ ひし形は,向かい合う2組の辺が平行で,4辺の長さがすべて等しい四角形のことをいいますが,
台形は,向かい合う1組の辺だけが平行な四角形なので,ひし形であるとはいえません。
イ ・・・ 正方形は,4つの角がすべて等しく,4辺の長さもすべて等しい四角形のことをいいますが,
長方形は,4つの角がすべて等しい四角形なので,正方形であるとはいえません。
ウ ・・・ 平行四辺形は,向かい合う2組の辺が平行な四角形のことをいいますが,
ひし形は,向かい合う2組の辺が平行で,4辺の長さがすべて等しい四角形なので,
平行四辺形であるといえます。
エ ・・・ 長方形は,4つの角がすべて等しい四角形のことをいいますが,
平行四辺形は,向かい合う2組の辺が平行な四角形で,4つの角がすべて等しくなるとは
限らないので,長方形であるとはいえません。
【参考】
平行四辺形は,向かい合う2組の辺が平行な四角形
ひし形は,向かい合う2組の辺が平行,さらに,4辺の長さがすべて等しい四角形
→ 4辺の長さがすべて等しい平行四辺形
長方形は,4つの角がすべて等しい四角形 (このとき,向かい合う2組の辺は必ず平行になる)
→ 4つの角がすべて等しい平行四辺形
正方形は,4つの角がすべて等しく,さらに,4辺の長さもすべて等しい四角形
→ 4つの角と4辺の長さがすべて等しい平行四辺形
なので,
ひし形,長方形,正方形は特殊な平行四辺形であるといえます。
大問5
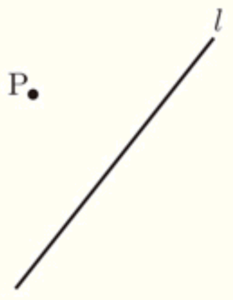
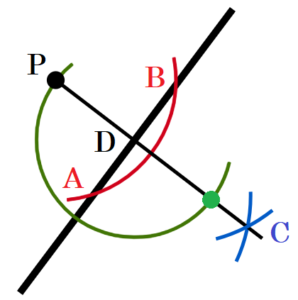
右の図で,点 \( P \) を,直線 \( l \) を対称の軸として対称移動させた点を作図によって求め,●印で示しなさい。
ただし,作図には定規とコンパスを用い,作図に使った線は消さないでおくこと。
【解答】
手順1 点 \( P \) を中心に 円弧を描く。
(直線 \( l \) との交点を \( A,B \) とします。)
手順2 2点 \( A,B \) を中心に 円弧を描く。
(交点を \( C \) とします。)
手順3 2点 \( C,P \) を通る直線を描く。
(直線 \( l \) との交点を \( D \) とします。)
手順4 点 \( D \) を中心に 線分 \( DP \) を半径とする円弧を描く。
手順4の円弧と手順3の直線の交点が求める点になります。
【解説】
点 \( P \) を,直線 \( l \) を対称の軸として対称移動させた点を 点 \( P’ \) とすると,
点 \( P’ \) は,点 \( P \) を通る直線 \( l \) の垂線上の点になります。
また,線分 \( DP \) と線分 \( DP’ \) の長さは等しくなります。
大問6
太郎さんは,令和2年から令和5年までの4年間について,自分が住んでいる町の風力発電所の供給電力量を調べました。次の表は,それぞれの年の1月から12月までの月ごとの供給電力量について,代表値をまとめたものです。また,下の図は,分布のようすを箱ひげ図に表したものです。
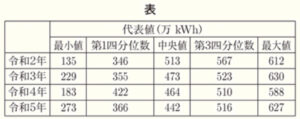
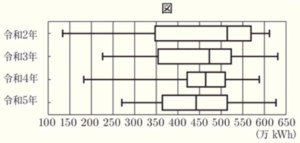
このとき,次の(1),(2)の問いに答えなさい。
(1) 令和5年の四分位範囲を求めなさい。
【解答】
\( 150 \) 万 \( kWh \)
【解説】
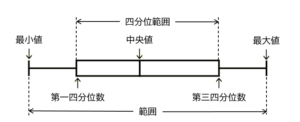
四分位範囲は,「第3四分位数 \( – \) 第1四分位数」で求めることができるので,
\( 516-366=150 \) 万 \( kWh \)
(2) 次のア~エのうち,太郎さんが住んでいる町の風力発電所の月ごとの供給電力量について,表や図から読み取れることとして正しいものはどれですか。一つ選び,その記号を書きなさい。
ア 4年間の中で範囲が最も大きいのは,令和3年である。
イ 令和4年は,供給電力量が \( 510 \) 万 \( kWh \) の月が必ずある。
ウ 令和3年は,供給電力量が \( 520 \) 万 \( kWh \) 以上だった月が少なくとも3つある。
エ 4年間の中で中央値が最も大きいのは令和2年であるから,平均値も最も大きい。
【解説】
ア ・・・ 範囲は,「最大値 \( – \) 最小値」で求めることができるので,
令和2年 ・・・ \( 612-135=477 \) 万 \( kWh \)
令和3年 ・・・ \( 630-229=401 \) 万 \( kWh \)
令和4年 ・・・ \( 588-183=405 \) 万 \( kWh \)
令和5年 ・・・ \( 627-273=354 \) 万 \( kWh \)
最も大きいのは,令和2年であり,正しくありません。
イ ・・・ 令和4年は,第3四分位数が \( 510 \) 万 \( kWh \) になっています。
1年は12か月なので,第3四分位数は小さい方から9番目と10番目の値の平均値になります。
2つの値の平均値が \( 510 \) になるのは \( 509 \) と \( 511 \) の場合も考えられるので,
正しくありません。
ウ ・・・ 令和3年は,第3四分位数が \( 523 \) 万 \( kWh \) なので,
小さい方から10番目の値は,\( 523 \) 万 \( kWh \) 以上の値であることがわかります。
つまり,小さい方から10番目,11番目,12番目 のの3つの月は
必ず \( 520 \) 万 \( kWh \) 以上値であることがわかります。
エ ・・・ 中央値の大小と平均値の大小は必ずしも一致するとは限らないので,正しくありません。
[例]
Aグループ \( \fbox{10 10 10 10 1000 } \) のとき,中央値は \( 10 \),平均値は \( 208 \)
Bグループ \( \fbox{100 100 100 100 200 } \) のとき,中央値は \( 100 \),平均値は \( 120 \)
となり,中央値はBグループの方が大きいが平均値はAグループの方が大きくなります。
大問7
さやかさんが住んでいる町の商店街で,イベントが開かれることになりました。このイベントでは,買い物をした人に賞品があたるくじ引きを行います。
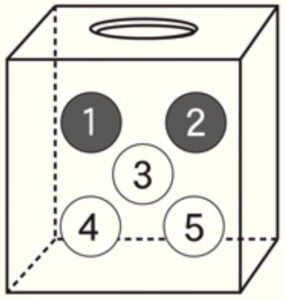
右の図のように,1,2の数字が1つずつ書いてある赤球2個と3,4,5の数字が1つずつ書いてある白球3個が箱の中に入っています。くじ引きでは,この箱の中から2個の球を取り出し,同じ色の球を取り出すと賞品があたります。
このとき,次の(1),(2)の問いに答えなさい。
(1) この箱の中から,同時に2個の球を取り出すとき,取り出した球に書いてある数字の組み合わせは全部で何通りありますか。
【解説】
同時に2個の球を取り出すということは,\( 1,2 \) と \( 2,1 \) は1通りと考えます。
取り出した球に書いてある数字の組み合わせを樹形図にして書き出すと,下の10通りになります。
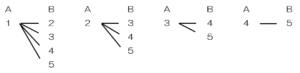
(2) このくじ引きの担当になったさやかさんのお父さんは,より多くの人に賞品があたるように2個の球を取り出す方法を考えています。
くじ引きをするとき,次のAの方法とBの方法のうち,賞品があたりやすいのは,Aの方法ですか,Bの方法ですか,どちらも同じですか。その理由を確率を用いて説明しなさい。
ただし,どの球を取り出すことも同様に確からしいものとします。
方法
A 球を1個取り出して球の色を確認する。取り出した球を箱の中にもどさずに,続けてもう1個取り出す。
B 球を1個取り出して球の色を確認した後,取り出した球を箱の中にもどし,再び箱の中から1個取り出す。
【解答】
賞品があたる確率は,Aの方法が \( \dfrac{2}{5} \),Bの方法が \( \dfrac{13}{25} \) で,Bの方法の方が大きいので,
賞品があたりやすいのは,Bの方法である。
【解説】
【Aの方法で景品があたる確率】
取り出した球に書いてある数字の組み合わせを樹形図にして書き出し,
賞品があたる組み合わせのところに
○ をつけると,
全ての組み合わせは20通り,景品があたる組み合わせは8通りなので,
確率は \( \dfrac{8}{20}=\dfrac{2}{5} \left(=\dfrac{10}{25} \right) \)

【Bの方法で景品があたる確率】
取り出した球に書いてある数字の組み合わせを樹形図にして書き出し,
賞品があたる組み合わせのところに ○ をつけると,
全ての組み合わせは25通り,景品があたる組み合わせは13通りなので,
確率は \( \dfrac{13}{25} \)

大問8
一郎さんは,\( 85 \) 円切手と \( 110 \) 円切手を合わせて \( 18 \) 枚買うために郵便局へ行きました。ところが,\( 85 \) 円切手と \( 110 \) 円切手それぞれの必要な枚数を間違えて,逆に注文したため,はじめに買う予定にしていた金額よりも \( 200 \) 円高くなりました。
このとき,一郎さんがはじめに買う予定にしていた \( 85 \) 円切手と \( 110 \) 円切手の枚数をそれぞれ求めなさい。
ただし,用いる文字が何を表すかを示して方程式をつくり,それを解く過程も書くこと。
【解答】
はじめに買う予定にしていた \( 85 \) 円切手の枚数を \( x \) 枚,\( 110 \) 円切手の枚数を \( y \) 枚とすると,
\( \left\{ \begin{array}{}
(85y+110x)-(85x+110y)=200 \;\; ・・・ \;\; ➀ \\
x+y=18 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀を整理すると,
\( 25x-25y=200 \)
\( x-y=8 \)
➀ \( + \) ➁すると,
\( 2x=26 \)
\( x=13 \)
➁に代入すると,
\( 13+y=18 \)
\( y=5 \)
よって,はじめに買う予定にしていた
\( 85 \) 円切手の枚数は \( 13 \) 枚,\( 110 \) 円切手の枚数は \( 5 \) 枚
【解説】
はじめに買う予定にしていた金額は,\( 85x+110y \)(円)
実際に注文した代金は,\( 85y+110x \)(円)
で,実際に注文した代金ははじめに買う予定にしていた金額より \( 200 \) 円高かったので,
金額の関係を表す方程式は,\( (85y+110x)-(85x+110y)=200 \) になります。
大問9
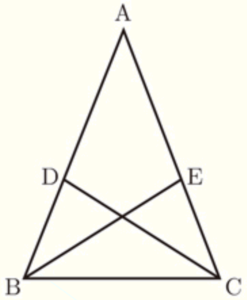
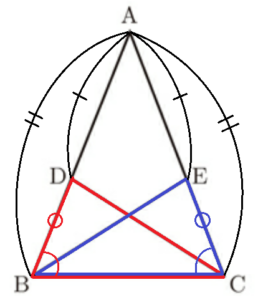
右の図のように,\( AB=AC \) である二等辺三角形 \( ABC \) があります。2点 \( D,E \) は,それぞれ辺 \( AB,AC \) 上の点で,\( AD=AE \) となるようにとります。
このとき,\( △DBC≡△ECB \) であることを証明しなさい。
【解答】
\( △DBC \) で \( △ECB \) において,
\( DB=AB-AD,EC=AC-AE \) であり,
仮定より \( AB=AC,AD=AE \) なので,
\( DB=EC \) ・・・ ➀
二等辺三角形の底角は等しいので,
\( ∠DBC=∠ECB \) ・・・ ➁
また,\( BC \) は共通 ・・・ ➂
➀➁➂より,2組の辺とその間の角がそれぞれ等しいので,
\( △DBC≡△ECB \)
大問10
ある企業は,ドローン(無人航空機) を利用して,A地点から海を挟んだB地点まで荷物を運ぶ計画を立てています。
このドローンは,海面からの高さ \( 2 \; m \) のA地点を出発します。毎秒 \( 4 \; m \) ずつ一定の割合で上昇し,出発してから \( 25 \) 秒後に水平飛行に移ります。水平飛行を \( 300 \) 秒間続けてから,一定の割合で下降し,出発してから \( 367 \) 秒後に海面からの高さ \( 18 \; m \) のB地点に到着します。
次の図は,ドローンがA地点を出発してからの時間を \( x \) 秒,海面からの高さを \( y \; m \) としたときの \( x \) と \( y \) の関係をグラフに表したものです。
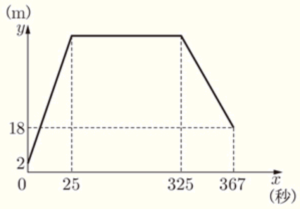
このとき,次の(1),(2)の問いに答えなさい。
(1) このドローンが水平飛行をしているとき,ドローンの海面からの高さは何 \( m \) ですか。
【解説】
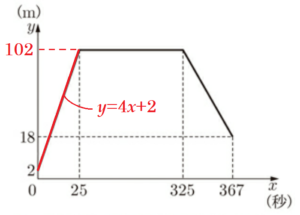
\( 0≦x≦25 \) の上昇中を表すグラフに注目すると,\( (0,2) \) を通り,傾きが \( 4 \) の直線なので,
この直線の式は \( y=4x+2 \) になります。
\( 25 \) 秒後に水平飛行に移るので,この式に \( x=25 \) を代入すると,
\( y=4 \times 25+2=102 \; (m) \)
(2) このドローンが海面からの高さ \( 50 \; m \) 以上を飛行しているのは,出発してから何秒後から何秒後までですか。その時間の範囲を求めなさい。
【解答】
\( 12 \) 秒後から \( 351 \) 秒後
【解説】
グラフに \( y=50 \) の直線を書き込むと,下の図のように2点で交わり,
緑の部分が高さ \( 50 \; m \) 以上を飛行しているときになります。
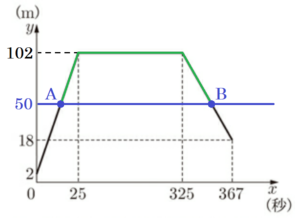
【 \( 0≦x≦25 \) で交わる点 \( A \)】
点 \( A \) は,\( y=4x+2 \) と \( y=50 \) の交点なので,
\( 4x+2=50 \)
\( x=12 \)
【 \( 325≦x≦367 \) で交わる点 \( B \)】
\( 325≦x≦367 \) における問題のグラフの直線は
\( (325,102),(367,18) \) の2点を通るので,
この直線の式を \( y=ax+b \) とすると,
\( a=\dfrac{18-102}{367-325}=-2 \)
\( y=-2x+b \) に \( x=325,y=102 \) を代入すると,
\( 102=-2 \times 325+b \)
\( 102=-650+b \)
\( b=752 \)
点 \( B \) は,\( y=-2x+752 \) と \( y=50 \) の交点なので,
\( -2x+752=50 \)
\( x=351 \)
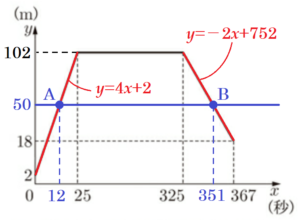
よって,高さ \( 50 \; m \) 以上を飛行しているのは,
出発してから \( 12 \) 秒後から \( 351 \) 秒後の間
大問11
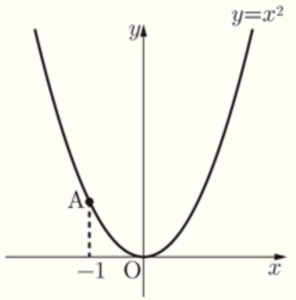
右の図のように,関数 \( y=x^2 \) のグラフ上に点 \( A \) があり,\( A \) の \( x \) 座標は \( -1 \) です。
このとき,次の(1)~(3)の問いに答えなさい。
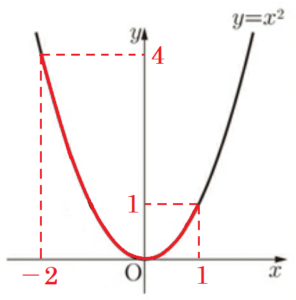
(1) 関数 \( y=x^2 \) について,\( x \) の変域が \( −2≦x≦1 \) のとき,\( y \) の変域を求めなさい。
【解説】
\( y=ax^2 \; (a>0) \) のグラフでは,
・ \( x \) の変域が \( 0 \) を含むとき,\( y \) の最小値は必ず \( 0 \) になります。
・ \( x \) の絶対値が最も大きいとき,\( y \) の値は必ず最大値をとります。
関数 \( y=x^2 \) について,
\( x \) の変域は \( −2≦x≦1 \) で,
\( 0 \) を含んでいるので, \( y \) の最小値は \( 0 \)。
\( x \) の絶対値が最も大きいのは
\( x=-2 \) のときなので,\( y \) の最大値は
\( y=(-2)^2=4 \)
よって,\( y \) の変域は \( 0≦y≦4 \)
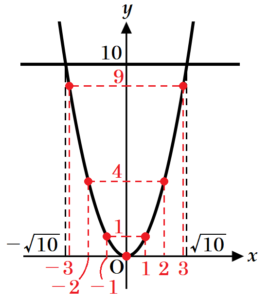
(2) 関数 \( y=x^2 \) のグラフ上で,\( y \) 座標が \( 10 \) 以下である点のうち,\( x \) 座標と \( y \) 座標がともに整数である点はいくつありますか。その個数を求めなさい。
【解説】
\( y=x^2 \) のグラフで,\( y \) 座標が \( 10 \) になるのは,
\( 10=x^2 \)
\( x=±\sqrt{10} \)
のときなので,\( y \) 座標が \( 10 \) 以下になるのは, \( −\sqrt{10}≦x≦\sqrt{10} \) のときです。
この範囲の中で \( x \) 座標が整数になるのは,
\( x=-3,-2,-1,0,1,2,3 \) のときです。
\( x=0 \) のとき,\( y=0 \)
\( x=±1 \) のとき,\( y=1 \)
\( x=±2 \) のとき,\( y=4 \)
\( x=±3 \) のとき,\( y=9 \)
で,\( y \) 座標も整数になっています。
よって,\( y \) 座標が \( 10 \) 以下である点のうち,\( x \) 座標と \( y \) 座標がともに整数である点は
\( (-3,9),(-2,4),(-1,1),(0,0),(1,1),(2,4),(3,9) \)
の7個になります。
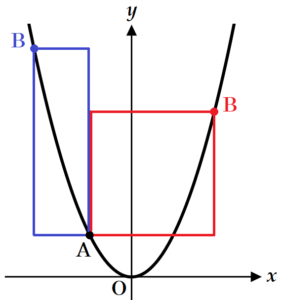
(3) 関数 \( y=x^2 \) のグラフ上に点 \( A \) よりも \( y \) 座標が大きい点 \( B \) をとります。線分 \( AB \) を対角線として辺が \( x \) 軸,\( y \) 軸と平行な長方形をつくるとき,その長方形の周の長さが \( 12 \) となる点 \( B \) の \( x \) 座標をすべて求めなさい。
【解答】
\( \dfrac{1-\sqrt{33}}{2},2 \)
【解説】
あてはまる点 \( B \) は,点 \( B \) の \( x \) 座標が点 \( A \) の \( x \) 座標より大きい場合と小さい場合の2つ存在します。
【点 \( B \) の \( x \) 座標が点 \( A \) より大きい場合】
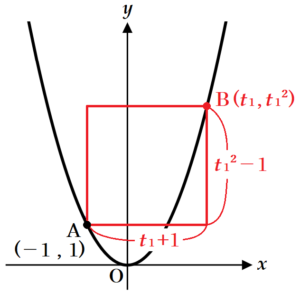
点 \( B \) の \( x \) 座標を \( t_1 \) とすると,
点 \( B \) の座標は \( (t_1,t_1\,^2) \) と表すことができます。
また,線分 \( AB \) を対角線とする長方形の
横の辺の長さは \( t_1+1 \),
縦の辺の長さは \( t_1\,^2-1 \)
と表すことができます。
このとき、この長方形の周の長さが \( 12 \) なので,
\( 2\{(t_1+1)+(t_1\,^2-1)\}=12 \)
\( t_1\,^2+t_1=6 \)
\( t_1\,^2+t_1-6=0 \)
\( (t_1-2)(t_1+3)=0 \)
\( t_1=2 \)
(\( t_1>-1 \) より)
\( \phantom{ } \)
【点 \( B \) の \( x \) 座標が点 \( A \) より小さい場合】
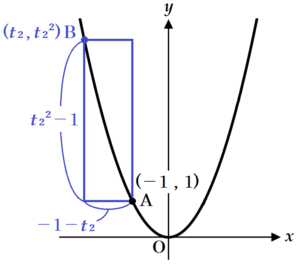
点 \( B \) の \( x \) 座標を \( t_2 \) とすると,
点 \( B \) の座標は \( (t_2,t_2\,^2) \) と表すことができます。
また,線分 \( AB \) を対角線とする長方形の
横の辺の長さは \( -1-t_2 \),
縦の辺の長さは \( t_2\,^2-1 \)
と表すことができます。
このとき、この長方形の周の長さが \( 12 \) なので,
\( 2\{(-1-t_2)+(t_2\,^2-1)\}=12 \)
\( t_2\,^2-t_2-2=6 \)
\( t_2\,^2-t_2-8=0 \)
\( t_2=\dfrac{1-\sqrt{33}}{2} \)
(\( t_2<-1 \) より)
\( \phantom{ } \)
大問12
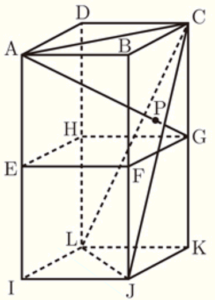
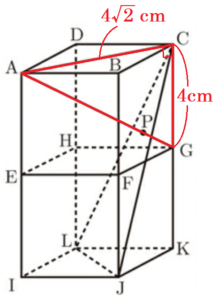
右の図は,1辺の長さが \( 4 \; cm \) の立方体を2つ重ね,直方体にしたものです。点 \( P \) は,線分 \( AG \) と3点 \( C,J,L \) をふくむ平面との交点です。
このとき,次の(1)~(3)の問いに答えなさい。
(1) 線分 \( AC \) の長さを求めなさい。
【解答】
\( 4\sqrt{2} \; cm \)
【解説】
線分 \( AC \) は,1辺 \( 4 \; cm \) の正方形 \( ABCD \) の対角線なので,
\( AC=\sqrt{2}AB=4\sqrt{2} \; (cm) \)
(2) 直方体 \( ABCD-IJKL \) の体積は,三角錐 \( CJKL \) の体積の何倍か求めなさい。
【解説】
直方体 \( ABCD-IJKL \) の体積 \( V_1 \) は,\( V_1= \) 四角形 \( IJKL \times CK \)
三角錐 \( CJKL \) の体積 \( V_2 \) は,\( V_2=△JKL \times CK \times \dfrac{1}{3} \)
で求めることができます。
線分 \( JL \) は,四角形 \( IJKL \) の対角線なので,
四角形 \( IJKL=2△JKL \)
であり,
\( V_2=△JKL \times CK \times \dfrac{1}{3} \) より,
\( 3V_2=△JKL \times CK \)
なので,
\( V_1= \) 四角形 \( IJKL \times OK \)
\( =2△JKL \times CK \)
\( =2 \times 3V_2 \)
\( =6V_2 \)
よって,直方体 \( ABCD-IJKL \) の体積 \( V_1 \) は,三角錐 \( CJKL \) の体積 \( V_2 \) の6倍になっています。
(3) 線分 \( AP \) の長さを求めなさい。
【解答】
\( \dfrac{16\sqrt{3}}{5} \; cm \)
【解説】
線分 \( AP \) は,立方体 \( ABCD-EFGH \) の対角線である線分 \( AG \) の一部であることから,
\( AP:PG \) の比がわかれば,線分 \( AP \) の長さを求めることができます。
【線分 \( AG \) の長さを求める】
\( △ACG \) は \( AC=4\sqrt{2} \; cm \),\( CG=4 \; cm \) の
直角三角形なので,三平方の定理より,
\( AG^2=(4\sqrt{2})^2+4^2=48 \)
\( AG=4\sqrt{3} \; (cm) \)
\( \phantom{ } \)
【\( AP:PG \) の比を求める】
面 \( IJKL \) の対角線の交点を \( M \),
線分 \( EG \) と線分 \( CM \) の交点を \( N \) とします。
\( \phantom{ } \)
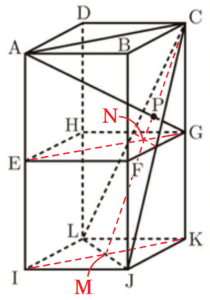
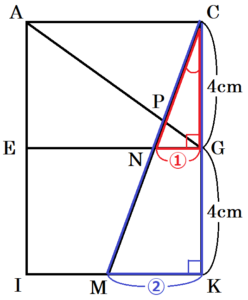
ここから,面 \( AIKC \) を書き出すと右の図のようになります。
\( △CNG \) と \( △CMK \) において,
\( ∠NCG=∠MCK \) (共通)
\( ∠CGN=∠CKM=90° \)
より,2組の角が等しいので,
\( △CNG \) ∽ \( △CMK \)
対する辺の比は等しいので,
\( NG:MK=CG:CK=1:2 \)
よって,\( MK=2NG \)
\( \phantom{ } \)
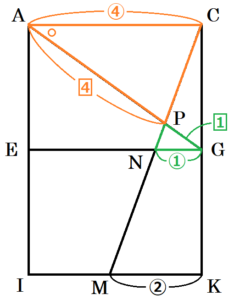
次に,\( △PAC \) と \( △PGN \) において,
立方体の向かい合う辺は平行なので,
\( AC//EG \) であり,錯角は等しいので,
\( ∠PAC=∠PGN \)
対頂角は等しいので,
\( ∠APC=∠GPN \)
より,2組の角が等しいので,
\( △PAC \) ∽ \( △PGN \)
正方形の対角線はそれぞれの中点で交わるので,
点 \( M \) は線分 \( IK \) の中点であり,
\( AC:MK=IK:MK=2:1 \)
よって,\( AC=2MK=4NG \)
対する辺の比は等しいので,
\( AP:GP=AC:GN=4:1 \)
よって,\( AP=\dfrac{4}{5}AG \)
\( \phantom{ } \)
\( AG=4\sqrt{3} \; cm \) であることから,
\( AP=\dfrac{4}{5}AG=\dfrac{4}{5} \times 4\sqrt{3}=\dfrac{16\sqrt{3}}{5} \; (cm) \)