大問1
1 次の(1)~(5)の問いに答えなさい。
(1) \( 7+18 \div 3 \) を計算しなさい。
【解説】
\( =7+6 \)
\( =13 \)
(2) \( \dfrac{3}{5}-\dfrac{1}{6} \times \dfrac{4}{5} \) を計算しなさい。
【解説】
\( =\dfrac{3}{5}-\dfrac{1 \times 4}{6 \times 5} \)
\( =\dfrac{3}{5}-\dfrac{2}{15} \)
\( =\dfrac{9}{15}-\dfrac{2}{15} \)
\( =\dfrac{7}{15} \)
(3) \( \sqrt{32}- \left( \dfrac{6}{ \sqrt{2}}+\sqrt{8} \right) \) を計算しなさい。
【解説】
\( =4\sqrt{2}-(3\sqrt{2}+2\sqrt{2}) \)
\( =4\sqrt{2}-5\sqrt{2} \)
\( =-\sqrt{2} \)
(4) \( 60 \) と \( 84 \) の最小公倍数を求めなさい。
【解説】
\( 60 \) と \( 84 \) の最小公倍数を \( N \) として,素因数分解したとき,
\( 60 \) に含まれる素数とその個数、\( 84 \) に含まれる素数とその個数をすべて含んでいます。
\( 60 \) と \( 84 \) を素因数分解すると,
\( 60=\color{red}{2^2} \times \color{red}{3} \times \color{blue}{5} \)
\( 84=\color{red}{2^2} \times \color{red}{3} \times \color{orange}{7} \)
であり,\( \color{red}{2^2} \times \color{red}{3} \) はどちらにも含まれていますが,
\( \color{blue}{5} \) が1個と \( \color{orange}{7} \) が1個は片方にしか含まれていません。
\( 60 \) の倍数でもあり,\( 84 \) の倍数でもあるためには,\( \color{blue}{5} \) と \( \color{orange}{7} \) が両方含まれている必要があるので,
最小公倍数は \( \color{red}{2^2} \times \color{red}{3} \times \color{blue}{5} \times \color{orange}{7}=420 \)
(5) 下のア~エのうち, その数の逆数が \( 1 \) より大きいものをすべて選び, 記号で答えなさい。
ア \( \dfrac{3}{4} \) イ \( 3 \) ウ \( -\dfrac{1}{2} \) エ \( 0.9 \)
【解説】
ある数に対してかけると \( 1 \) になる数を逆数といいます。
例えば \( \dfrac{2}{3} \times \dfrac{3}{2}=1 \) なので,\( \dfrac{2}{3} \) の逆数は \( \dfrac{3}{2} \) になります。
つまり,「逆数とは分子と分母を入れ替えた数である」ともいえます。
ア~エそれぞれの逆数は,
ア \( \dfrac{4}{3} \) イ \( \dfrac{1}{3} \) ウ \( -2 \) エ \( \dfrac{10}{9} \)
なので,\( 1 \) より大きいのは,アとエになります。
2 2次方程式 \( x^2-3x+1=0 \) を解きなさい。
【解答】
\( x=\dfrac{3±\sqrt{5}}{2} \)
【解説】
解の公式より,
\( x=\dfrac{-(-3)±\sqrt{(-3)^2-4 \times 1 \times 1}}{2 \times 1} \)
\( =\dfrac{3±\sqrt{5}}{2} \)
3 \( a \) を正の数,\( b \) を負の数とするとき,式の値がいつも正の数になるものを,下のア~エの中からすべて選び,記号で答えなさい。
ア \( 2a+b \) イ \( a-3b \) ウ \( 3-a-b \) エ \( (ab)^2 \) ²
【解答】
イ \( a-3b \)
エ \( (ab)^2 \)
【解説】
【アとウの反例】
ア ・・・ \( a=1,b=-5 \) のとき
\( 2a+b=2 \times 1+(-5) \)
\( =2-5 \)
\( =-3 \)
\( \phantom{あああ} \)
ウ ・・・ \( a=5,b=-1 \) のとき
\( 3-a-b=3-5-(-1) \)
\( =3-5+1 \)
\( =-1 \)
4 反比例 \( y=\dfrac{2}{x} \) の式がある。\( x \) の変域を \( 1≦x≦3 \) とするとき,\( y \) の変域を求めなさい。
【解答】
\( \dfrac{2}{3}≦y≦2 \)
【解説】
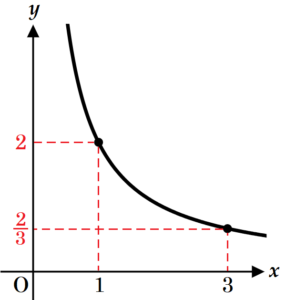
\( y=\dfrac{2}{x} \) のグラフは右の図のような曲線であり,
\( x \) の値が大きくなるほど \( y \) の値は小さくなります。
\( x=1 \) のとき,\( y=\dfrac{2}{1}=2 \)
\( x=3 \) のとき,\( y=\dfrac{2}{3} \)
なので,\( y \) の変域は \( \dfrac{2}{3}≦y≦2 \) になります。
5 かごしま水族館で,イルカが \( 185 \; m \) の距離を \( 37 \) 秒で泳いでいました。このとき,イルカの泳ぐ速さは分速何 \( m \) であったか求めなさい。ただし,イルカは一定の速さで泳ぐものとします。
【解説】
\( 185 \; m \) の距離を \( 37 \) 秒で泳いでいたことから,
イルカの泳ぐ速さは秒速 \( \dfrac{185}{37}=5 \; (m) \) なので,
分速になおすと,
秒速 \( 5 \; m \; = \) 分速 \( 5 \times 60=300 \; m \)
になります。
大問2
1 大小2つのさいころを同時に投げるとき.出る目の積が素数になる確率を求めなさい。
【解説】
素数とは1とその数自身以外に約数を持たない数なので,出る目の積 \( N \) が素数になるとき,
\( N=1 \times \) 素数 または \( N= \) 素数 \( \times 1 \)
で表すことができます。
つまり,出る目の積 \( N \) が素数になるのは,
どちらかのさいころの出た目が \( 1 \),もう一方のさいころの出た目が素数のときです。
ちなみに,\( 1 \) から \( 6 \) までの数のうち,素数は \( 2,3,5 \) の3つです。
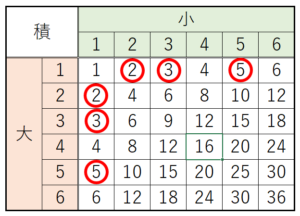
大小2つのさいころの出る目の組み合わせと
その積を表に書き出し,
積が素数になるところに ○ をつけてみます。
積が素数になる組み合わせは \( 6 \) 通り
すべての組み合わせは \( 36 \) 通り
なので,求める確率は
\( \dfrac{6}{36}=\dfrac{1}{6} \)
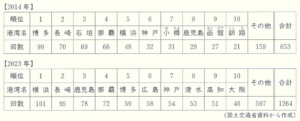
2 下の表は,2014年と2023年の日本における外国の船会社が運航するクルーズ船の寄港回数の多い港湾名と回数をそれぞれ示したものです。日本における外国の船会社が運航するクルーズ船の寄港回数の合計に対する鹿児島への寄港回数の割合が高かったのは,2014年と2023年のどちらですか。解答欄の「2014年」と「2023年」のどちらかを ○ で囲みなさい。また,その年の寄港回数の合計に対する鹿児島への寄港回数の割合は,何%にあたるか求めなさい。ただし,小数第2位を四捨五入することとします。
【解答】
2023年
寄港回数の割合 ・・・ \( 6.2 \; \% \)
【解説】
ある物事(回数や個数,人数など)が全体に占める割合(%)は
ある物事の数 \( \div \) 全体の数 \( \times 100 \)
で求めることができます。
【2014年の鹿児島への寄港回数の割合】
鹿児島への寄港回数は \( 29 \) 回,日本全体の合計寄港回数は \( 653 \) 回なので,
鹿児島への寄港回数の割合は,\( \dfrac{29}{653} \times 100=4.44・・・ \; (\%) \)
小数第2位を四捨五入すると,\( 4.44・・・ → 4.4 \; \% \)
【2023年の鹿児島への寄港回数の割合】
鹿児島への寄港回数は \( 78 \) 回,日本全体の合計寄港回数は \( 1264 \) 回なので,
鹿児島への寄港回数の割合は,\( \dfrac{78}{1264} \times 100=6.17・・・ \; (\%) \)
小数第2位を四捨五入すると,\( 6.17・・・ → 6.2 \; \% \)
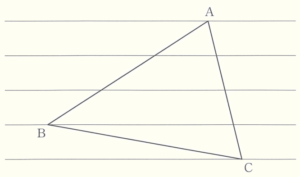
3 下の図のような等間隔で平行に罫線が引かれているノートがあり,\( △ABC \) の各頂点が罫線上にあります。\( BP:PC=2:1 \) となるように辺 \( BC \) 上の点 \( P \) を定規とコンパスを用いて作図しなさい。ただし,点 \( P \) の位置を示す文字 \( P \) も書き入れ,作図に用いた線も残しておきなさい。
【解答】
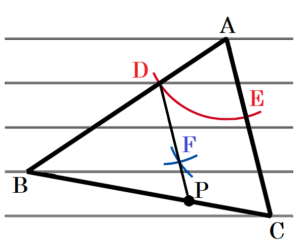
手順1 辺 \( AB \) と上から2番目の罫線の交点を \( D \)
とし,\( AD \) を半径とする円弧を描く。
(辺 \( AC \) との交点を \( E \) とします。)
手順2 2点 \( D,E \) を中心に,\( AD \) を半径とする
円弧を描く。
(交点を \( F \) とします。)
手順3 2点 \( D,F \) を通る直線を描く。
手順3の直線と辺 \( BC \) の交点が求める点 \( P \) になります。
【解説】
「等間隔で平行に罫線」が引かれていることに
注目すると,辺 \( AB \) と上から2番目の罫線の
交点を \( D \) としたとき,\( BD:DA=2:1 \) に
なっています。
さらに,\( BP:PC=2:1 \) でもあるので,
補助線 \( DP \) をひくと,\( △DBP \) ∽ \( △ABC \)
になります。
ここから,\( DP//AC \) になるので,
「点 \( D \) を通り,辺 \( AC \) と平行な直線」
を作図すればいいことになります。
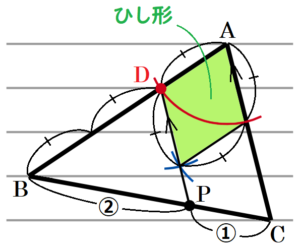
【点 \( D \) を通り,辺 \( AC \) と平行な直線の作図】
ひし形(平行四辺形)の向かい合う辺は平行なので,\( AD \) と同じ長さの線分を3つ作図することで
点 \( D \) を通り,辺 \( AC \) と平行な直線を作図することができます。
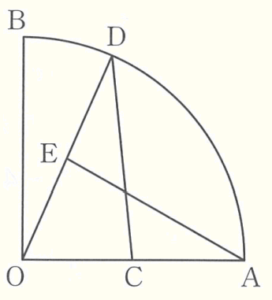
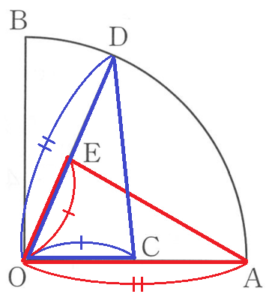
4 右の図のような中心角 \( 90° \) のおうぎ形 \( OAB \) があり, 線分 \( OA \) の中点を \( C \) とし,弧 \( AB \) 上に点 \( D \) をとり,線分 \( OD \) の中点を \( E \) とします。\( △AOE≡△DOC \) であることを証明しなさい。
【解答】
\( △AOE \) と \( △DOC \) において,
仮定より,
\( OA=OD \) ・・・ ➀
2点 \( C,E \) はそれぞれ線分 \( OA,OD \) の
中点なので,
\( OE=OC \) ・・・ ➁
共通な角なので,
\( ∠AOE=∠DOC \) ・・・ ➁
➀➁➂より,
2組の辺とその間の角がそれぞれ等しいので,
\( △AOE≡△DOC \)
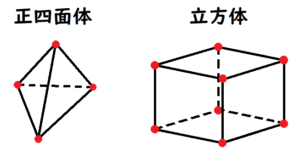
5 正四面体と立方体の模型がそれぞれ何個かあります。これらの模型の面の総数が \( 128 \) 面,頂点の総数が \( 156 \) 個であるとき, 正四面体と立方体の模型の個数をそれぞれ求めなさい。ただし,正四面体の模型を \( x \) 個,立方体の模型を \( y \) 個として,その方程式と計算過程も書きなさい。
【解答】
正四面体の面の数は \( 4 \) 面,立方体の面の数は \( 6 \) 面なので,
面の数の関係を方程式で表すと,\( 4x+6y=128 \) ・・・ ➀
正四面体の頂点の数は \( 4 \) 個,立方体の頂点の数は \( 8 \) 個なので,
頂点の数の関係を方程式で表すと,\( 4x+8y=156 \) ・・・ ➁
➀➁を連立方程式として解くと,
\( \left\{ \begin{array}{}
4x+6y=128 \;\; ・・・ \;\; ➀ \\
4x+8y=156 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁ \( – \) ➀ すると,
\( 2y=28 \)
\( y=14 \)
➀ に代入すると,
\( 4x+6 \times 14=128 \)
\( 4x=44 \)
\( x=11 \)
よって,正四面体の模型は \( 11 \) 個,立方体の模型は \( 14 \) 個
【解説】
正四面体は,合同な正三角形を4つくっつけてできる正多面体,
立方体(正六面体)は,合同な正方形を6つくっつけてできる正多面体
のことをいいます。
大問3
下の表は,2024年に開催されたパリオリンピックにおける男子バレーボール日本チームに登録された選手の背番号と身長をまとめたものです。また,図は出場12か国の登録された選手12人ずつの身長を箱ひげ図で表したものです。なお,各選手の身長はすべて整数で表されています。 次の1~4の問いに答えなさい。

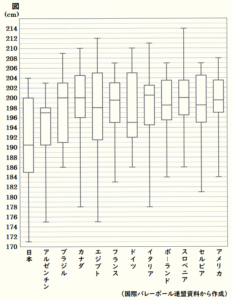
1 日本チームに登録された選手の身長の平均値を求めなさい。
【解説】
\( (187+200+183+190+195+204+175+202+188+191+200+171) \div 12=190.5 \; (cm) \)
2 下のア~エのヒストグラムのうち,図のフランスチームと同じデータを使ってまとめたものはどれですか。最も適当なものを下のア~エの中から1つ選び,記号で答えなさい。なお,ア~エにおいて,例えば,\( 182 \; cm \) 以上 \( 188 \; cm \) 未満の選手がそれぞれ1人いたことを表しています。
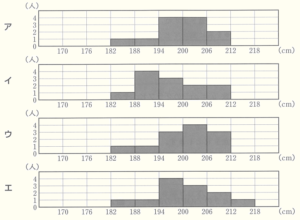
【解説】
箱ひげ図から最大値は \( 207 \; cm \) なので,
\( 212 \; cm \) 以上 \( 218 \; cm \) 未満の選手が1人いることになっている エ のヒストグラムはあてはまりません。
この箱ひげ図は12人のデータをまとめたものなので,
第一四分位数は \( 195 \; cm \) で,身長の低い方から3番目と4番目の値の平均値
中央値は \( 199.5 \; cm \) で,身長の低い方から6番目と7番目の値の平均値
第三四分位数は \( 203 \; cm \) で,身長の高い方から3番目と4番目の値の平均値
になります。
第一四分位数に注目すると,3番目と4番目の値の平均値が \( 195 \; cm \) なので,
4番目の値は \( 195 \; cm \) 以上であることがわかります。
イ のヒストグラムは,4番目の値が \( 188 \; cm \) 以上 \( 194 \; cm \) 未満の階級に属しているので,
あてはまりません
中央値に注目すると,6番目と7番目の値の平均値が \( 199.5 \; cm \) なので,
6番目の値は \( 199.5 \; cm \) 以下であることがわかります。
ウ のヒストグラムは,6番目の値が \( 200 \; cm \) 以上 \( 206 \; cm \) 未満の階級に属しているので,
あてはまりません
以上より、残った ア のヒストグラムが正解になります。
3 図の箱ひげ図から読み取れることとして,次の①~④は「正しい」,「正しくない」,「図からはわからない」のどれですか。最も適当なものを下のア~ウの中からそれぞれ1つ選び,記号で答えなさい。
➀ 最も身長が高い選手は,スロベニアチームにいる。
➁ 出場 12 か国の登録された選手のうち,6番目に身長が高い選手はブラジルチームにいる。
➂ 第3四分位数が最も大きいチームは,アメリカチームである。
➃ 四分位範囲が最も小さいチームは,ポーランドチームである。
ア 正しい イ 正しくない ウ 図からはわからない
【解答】
➀ ・・・ ア
➁ ・・・ ウ
➂ ・・・ イ
➃ ・・・ イ
【解説】
➀ 箱ひげ図の最大値が最も大きい(高い位置にある)のはスロベニアの箱ひげ図なので,正しい。
➁ 最大値だけで順番をつけるとブラジルの \( 209 \; cm \) が6番目になりますが,
スロベニアやエジプトの2番目に高い人の身長がわからないため,
\( 209 \; cm \) より高い可能性があります。
よって,この箱ひげ図からはわかりません。
➂ 第3四分位数が最も大きいチームは,エジプトとドイツで \( 205 \; cm \) になっています。
➃ 四分位範囲が最も小さいチームは,アメリカで \( 6.5 \; cm \) になっています。
4 下のデータは,図のドイツチームに登録された12人の選手のうち,11人の選手の身長を低い方から順に並べかえたものです。図を利用して,残り1人の身長として考えられる整数の値をすべて求めなさい。
11人の選手の身長 \( (cm) \)
\( 186 \quad 190 \quad 191 \quad 193 \quad 194 \quad 196 \quad 200 \quad 204 \quad 206 \quad 208 \quad 210 \)
【解答】
\( 193 \; cm,194 \; cm \)
【解説】
この箱ひげ図は12人のデータをまとめたもので,
第一四分位数は \( 192 \; cm \) で,身長の
低い方から3番目と4番目の値の平均値
中央値は \( 195 \; cm \) で,身長の
低い方から6番目と7番目の値の平均値
第三四分位数は \( 205 \; cm \) で,身長の
高い方から3番目と4番目の値の平均値
になっています。
問題のデータから,
身長の低い方から3番目 \( 191 \; cm \) と4番目 \( 193 \; cm \) の値の平均値は
\( \dfrac{191+193}{2}=192 \; (cm) \)
であり,箱ひげ図の第一四分位数の値と一致しています。
身長の低い方から6番目 \( 196 \; cm \) と7番目 \( 200 \; cm \) の値の平均値は
\( \dfrac{196+200}{2}=198 \; (cm) \)
であり,箱ひげ図の中央値より大きい値になっています。
身長の高い方から3番目 \( 204 \; cm \) と4番目 \( 206 \; cm \) の値の平均値は
\( \dfrac{204+206}{2}=205 \; (cm) \)
であり,箱ひげ図の第三四分位数の値と一致しています。
これらのことから,6番目と7番目の値の平均値が \( 195 \; cm \) になるためには
6番目と7番目の値が何\( \; cm \) になるのかを考えていきます。
6番目と7番目の値の平均値が \( 195 \; cm \) であるとき,
6番目の値は,\( 195 \; cm \) 以下,7番目の値は,\( 195 \; cm \) 以上
になります。 → 詳細は下の「2つの数A,Bと平均値の関係」を参照。
まず,11人の選手の中に \( 195 \; cm \) の人がいないことから,
追加される値が \( 195 \; cm \) ではないことは明らかです。
(平均値が \( 195 \; cm \) になるためには,\( 195 \; cm \) の選手が2人必要なため)
よって,11人の選手の身長のうち,\( 195 \; cm \) 以上で最も低いのは \( 196 \; cm \) であることから,
7番目の値は \( 196 \; cm \) になります。
このとき,6番目の値を \( n \; cm \) とすると,
\( \dfrac{n+196}{2}=195 \)
\( n=194 \; (cm) \)
より,6番目の値は \( 194 \; cm \) になります。
ここから,追加される値は \( \color{red}{194 \; cm} \) 以下であることがわかります。
また,箱ひげ図とデータで第一四分位数の値が一致していることから,
身長の低い方から4番目の値 \( 193 \; cm \) は変わらないので,
追加される値は \( \color{red}{193 \; cm} \) 以上であることがわかります。
これらのことから,追加される値は \( 193 \; cm \) または \( 194 \; cm \) のどちらかになります。
2つの数A,Bと平均値の関係
2つの数 \( A,B \;(A≦B) \) の平均値が
\( 195 \) であるとき,\( A,B \) がどのような数になるのか考えてみます。
【\( A=B \) のとき】
\( \dfrac{A+B}{2}=195 \) なので,
\( \dfrac{A+B}{2}=195 \)
\( \dfrac{A+A}{2}=195 \)
\( A=195 \)
よって,\( A=B \) であるとき,\( A,B \) はどちらも平均値と一致します。
【\( A<B \) の場合】
\( A \) の値について
\( \dfrac{A+B}{2}=195 \) なので,
\( B=A+x \; (x>0) \) とすると,
\( \dfrac{A+(A+x)}{2}=195 \)
\( \dfrac{2A+x}{2}=195 \)
\( A=195-\dfrac{x}{2} \)
よって,\( A<B \) であるとき,
\( A \) の値は平均値より小さい値になります。
\( \phantom{あああ} \)
\( B \) の値について
\( \dfrac{A+B}{2}=195 \) なので,
\( A=B-x \; (x>0) \) とすると,
\( \dfrac{(B-x)+B}{2}=195 \)
\( \dfrac{2B-x}{2}=195 \)
\( B=195+\dfrac{x}{2} \)
よって,\( A<B \) であるとき,
\( B \) の値は平均値より大きい値になります。
これらをまとめると,
2つの数 \( A,B \;(A≦B) \) とその平均値の関係は
\( A \) の値は必ず平均値以下,\( B \) の値は必ず平均値以上
になります。
大問4
ユウさんとレンさんは,授業中にタブレット端末でグラフ作成アプリを使って,関数 \( y=ax^2 \) について調べています。下は授業のある場面での【会話】です。次の1~4の問いに答えなさい。
【会話】
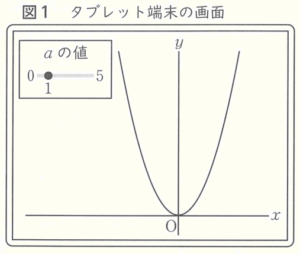
先生:今日は関数 \( y=ax^2 \) について,グラフ作成
アプリを使って考えていきましょう。まずは,
\( a=1 \) とすると画面(図1)のようなグラフ
が表示されますね。
ユウ:画面の●を左右に動かすとグラフの形が \( a \) の
値に対応するように動きますね。
レン:本当だ。➀【画面の●を右に動かすとグラフの
開き方が変化したよ。】
先生:では,次の【問題】を考えてみましょう。
\( \phantom{あああ} \)
【問題】
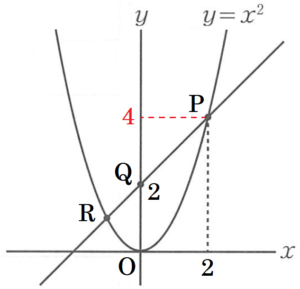
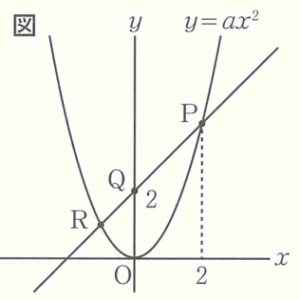
右の図のように,関数 \( y=ax^2 \) のグラフと,そのグラフ上に \( x \) 座標が \( 2 \) である点 \( P \) があり,点 \( Q \) の座標は \( (0,2) \) とします。また,直線 \( PQ \) と関数 \( y=ax^2 \) のグラフの2つの交点のうち,\( P \) でない方の点を \( R \) とします。このとき,\( △OPR \) の面積が \( 5 \) となるような \( a \) の値を求めなさい。ただし,\( a>0 \) とします。
ユウ:まずは,\( a=1 \) のときの \( △OPR \) の面積を
考えてみようよ。
レン:➁【\( a=1 \) のときの直線 \( PQ \) の式を求められ
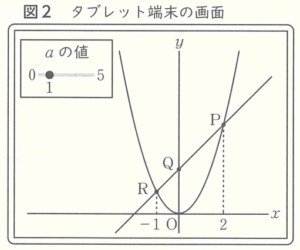
たよ。】タブレット端末に直線 \( PQ \) の式を
入力すると,点 \( P,R \) が画面(図2)の
ようになったよ。
ユウ:\( △OPR \) の面積は \( △OPQ \) と \( △OQR \) の
面積の和を求めたら良さそうだね。一緒に
考えてみよう。
レン:よし。\( △OPR \) の面積を求められたよ。
先生:正解です。よくできていますね。
ユウ:この調子で \( △OPR \) の面積が \( 5 \) のときの \( a \) の値を求めてみようよ。
レン:どのように考えていけばいいかな。
ユウ:画面の●を左右に動かしたら何かわかるかもしれないよ。
レン:\( a \) の値によって2点 \( P,Q \) を通る1次関数のグラフが右下がりになるときがあるよ。
先生:よいところに気づきましたね。画面の●を左右に動かしてみると他にも気づくことがありそうですね。
では,【問題】を解いてみましょう。
1 ①【 】について,レンさんが画面の●を右に動かしたとき,グラフの開き方はどのように変化しましたか。「大きくなる」と「小さくなる」のどちらかを選びなさい。
【解説】
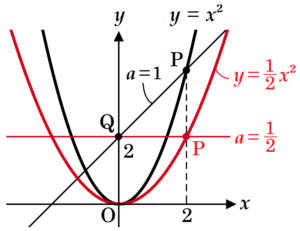
画面の●を右に動かすと,\( y=ax^2 \) の \( a \) の値が大きくなっていきます。
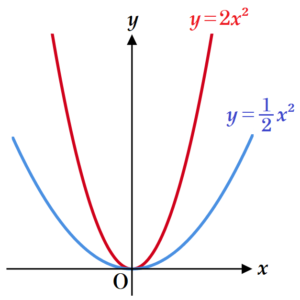
例として \( a=\dfrac{1}{2} \) の場合と \( a=2 \) の場合のグラフを書くと次のようになり,
\( a \) の値が大きくなると,グラフの開き方は小さくなります。
2 \( a=1 \) のとき,次の(1),(2)の問いに答えなさい。
(1) ②【 】について,直線 \( PQ \) の式を求めなさい。
【解説】
\( a=1 \) のとき,点 \( P \) の \( x \) 座標は,
\( y=2^2=4 \)
直線 \( PQ \) は \( P(2,4),Q(0,2) \) を通るので,
直線 \( PQ \) の傾きは,
傾き \( =\dfrac{4-2}{2-0}=1 \)
よって,直線 \( PQ \) の式は,\( y=x+2 \)
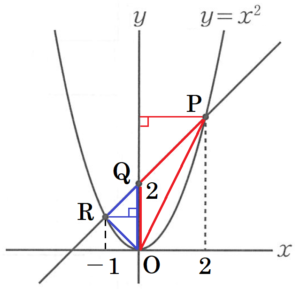
(2) ③【 】について,タブレット端末の画面(図2)を確認すると,点 \( R \) の \( x \) 座標が \( -1 \) でした。このとき,\( △OPQ \) と \( △OQR \) の面積をそれぞれ求めなさい。
【解答】
\( △OPQ=2 \),\( △OQR=1 \)
【解説】
\( △OPQ \) において,線分 \( OQ \) を底辺と考えると,
\( △OPQ=2 \times 2 \times \dfrac{1}{2}=2 \)
\( △OQR \) において,線分 \( OQ \) を底辺と考えると,
\( △OQR=2 \times 1 \times \dfrac{1}{2}=1 \)
3 ④【 】について,2点 \( P,Q \) を通る1次関数のグラフが右下がりになるような,\( a \) の値を下のア~エの中からすべて選び,記号で答えなさい。
ア \( a=\dfrac{1}{2} \) イ \( a=\dfrac{4}{3} \) ウ \( a=\dfrac{1}{4} \) エ \( a=\dfrac{2}{5} \)
【解答】
ウ \( a=\dfrac{1}{4} \),エ \( a=\dfrac{2}{5} \)
【解説】
直線 \( PQ \) が水平(\( x \) 軸と平行)になるのは,
点 \( P \) の座標が \( P(2,2) \) のときなので,
\( y=ax^2 \) に \( x=2,y=2 \) を代入すると,
\( 2=a \times 2^2 \)
\( a=\dfrac{1}{2} \)
\( a=1 \) のとき,直線 \( PQ \) は右上がり,
\( a=\dfrac{1}{2} \) のとき,直線 \( PQ \) は水平であることから,
直線 \( PQ \) が右下がりになるのは,
\( 0<a<\dfrac{1}{2} \) のときになります。
よって,あてはまるのは ウ,エ になります。
4 【会話】中にある【問題】を解きなさい。ただし,求め方や計算過程も書きなさい。
【解答】
\( △OPR=△OPQ+△OQR \) であり,
\( △OPQ \) の面積は,
\( △OPQ=2 \times 2 \times \dfrac{1}{2}=2 \)
なので,\( △OPR=5 \) になるのは,
\( △OQR=3 \) のとき。
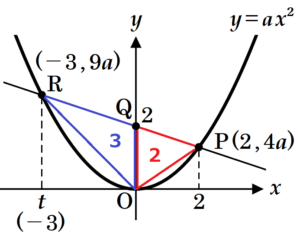
\( △OQR=3 \) になるときの
点 \( R \) の \( x \) 座標を \( t \) とすると,
\( △OQR=3 \)
\( 2 \times (-t) \times \dfrac{1}{2}=3 \)
\( t=-3 \)
となり,このときの点 \( R \) の座標は
\( R(-3,9a) \) と表すことができる。
点 \( P \) の座標は \( P(2,4a) \) と表すことができるので,
直線 \( PR \) の式を \( y=mx+2 \) とすると,
\( m=\dfrac{4a-9a}{2-(-3)}=-a \)
であり,直線 \( PR \) の式は \( y=-ax+2 \)
\( x=2,y=4a \) を代入すると,
\( 4a=-2a+2 \)
\( 6a=2 \)
\( a=\dfrac{1}{3} \)
大問5
ユウさんとレンさんは,図形のもつ性質や関係について調べています。 下の【会話】を読み,次の1~4の問いに答えなさい。
【会話】
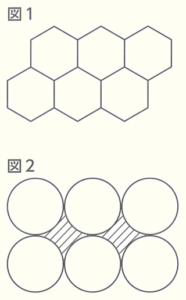
ユウ:昨日ハチの巣を見つけたんだけど,ハチの巣穴は六角形の形をしていること(図1)が多いよね。
円とか他の形でも良さそうなのにどうしてだろう。調べてみようよ。
レン:今,調べてみたら,巣を作る上で正六角形は合理的な形なん
だって。合同な正多角形を使ってすき間なくしきつめること
ができるのは,正三角形,正方形,正六角形の3種類しか
存在しないようだよ。
ユウ:確かに,円だと無駄なすき間(図2の斜線部分)ができてし
まうね。正六角形の1つの内角の大きさは ア 度であ
るから,正六角形をすき間なくしきつめることができるね。
レン:そして ➀【その3種類の正多角形の周の長さが等しいとき,それぞれの面積を求める】と各図形の
面積比がわかったよ。このことから,正三角形,正方形,正六角形の面積が等しいとき,それぞれの
周の長さを比較すると正六角形の周の長さが イ ということがわかるね。
ユウ:正六角形は面白い性質をもっているんだね。そういえば,②【アルキメデスは円周率の値を求める
ために,最初は正六角形の周の長さを利用して考えた】ようだよ。
レン:面白そうだね。実際に計算で求めてみよう。
1 ア に入る角度を求めなさい。
【解説】
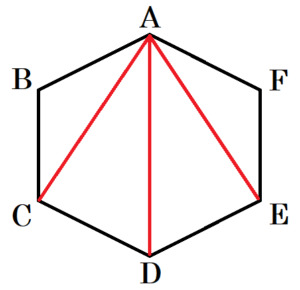
右の図のように頂点 \( A \) から対角線をひくと3本ひくことができ,
4つの三角形ができます。
三角形の内角の和は \( 180° \) なので,すべての内角の和は
\( 180° \times 4=720° \)
正六角形の内角はすべて等しいので,1つの内角の大きさは,
\( \dfrac{720°}{6}=120° \)
2 ➀【 】について,正三角形,正方形,正六角形の面積をそれぞれ \( S,T,U \) とします。3種類の各図形の周の長さを \( 12a \)(\( a \) は正の定数)として,\( S,T,U \) の値をそれぞれ \( a \) を用いて表しなさい。
【解答】
\( S=4\sqrt{3}a^2 \)
\( T=9a^2 \)
\( U=6\sqrt{3}a^2 \)
【解説】
【正三角形の面積】
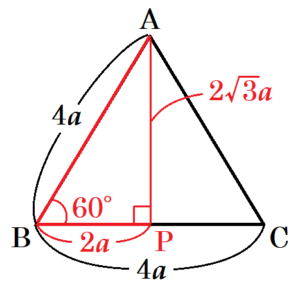
正三角形 \( ABC \) において,3つの辺の長さは等しいので,
\( AB=BC=\dfrac{12a}{3}=4a \)
点 \( A \) から辺 \( BC \) に垂線をひいた交点を \( P \) とすると,
\( △ABP \) は \( 30°,60°,90° \) の直角三角形になるので,
\( BP=\dfrac{1}{2}AB=2a,AP=\dfrac{\sqrt{3}}{2}AB=2\sqrt{3}a \)
よって,正三角形 \( ABC \) の面積 \( S \) は,
\( S=4a \times 2\sqrt{3}a \times \dfrac{1}{2}=4\sqrt{3}a^2 \)
【正方形の面積】
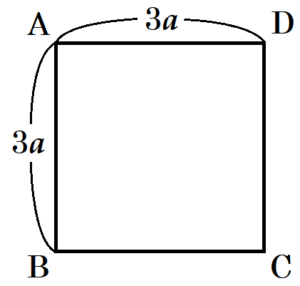
正方形 \( ABCD \) において,4つの辺の長さは等しいので,
\( AB=AD=\dfrac{12a}{4}=3a \)
よって,正方形 \( ABCD \) の面積 \( T \) は,
\( T=3a \times 3a=9a^2 \)
【正六角形の面積】
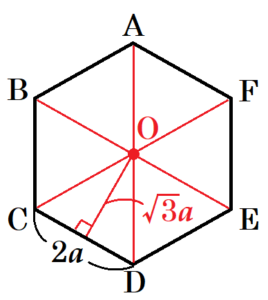
正六角形 \( ABCDEF \) において,6つの辺の長さは等しいので,
\( CD=\dfrac{12a}{6}=2a \)
対角線 \( AD,BE,CF \) をひくと3本の対角線は1点で交わり,
6個の合同な正三角形ができます。
3本の対角線の交点を \( O \) とすると,
\( △OCD \) は1辺の長さが \( 2a \) の正三角形なので,その面積は,
\( △OCD=2a \times \sqrt{3}a \times \dfrac{1}{2}=\sqrt{3}a^2 \)
正六角形 \( ABCDEF \) の面積 \( U \) は,
\( △OCD \) の6個分なので,
\( U=\sqrt{3}a^2 \times 6=6\sqrt{3}a^2 \)
3 イ に入ることばとして最も適当なものを,下のア~ウの中から1つ選び記号で答えなさい。
ア 正三角形と正方形の周の長さと等しい
イ 正三角形と正方形の周の長さよりも長い
ウ 正三角形と正方形の周の長さよりも短い
【解答】
ウ 正三角形と正方形の周の長さよりも短い
【解説】
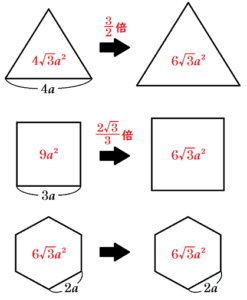
2 より,\( S<T<U \) なので,1辺の長さが \( 4a \) の正三角形と1辺の長さが \( 3a \) の正方形を
1辺の長さが \( 2a \) の正六角形と同じ面積になるように同じ形のまま変形すると,
正三角形の面積 ・・・ \( \dfrac{6\sqrt{3}a^2}{4\sqrt{3}a^2}=\dfrac{3}{2} \) 倍
正方形の面積 ・・・ \( \dfrac{6\sqrt{3}a^2}{9a^2}=\dfrac{2\sqrt{3}}{3} \) 倍
に拡大されます。
相似な図形の面積比は相似比の2乗の比と等しいので,
面積が大きくなるとそれぞれの図形の辺の長さも長くなります。
つまり,正六角形の周の長さはそのままで,正三角形と正方形の周の長さは長くなるので,
正六角形の周の長さは「正三角形と正方形の周の長さよりも短い」ということになります。
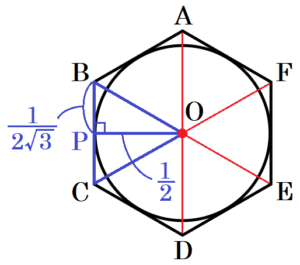
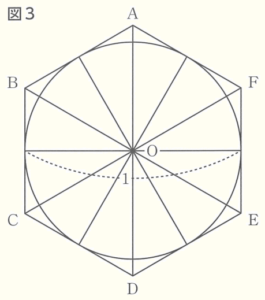
4 ②【 】について,円周率の近似値は,円周の長さが円の外側に接する正多角形の周の長さより小さいことを利用して考えることもできます。図3のように,直径 \( 1 \) の円 \( O \) とこの円の外側に接する正六角形 \( ABCDEF \) があります。このとき,円 \( O \) の円周の長さは \( \pi{} \) となります。次の(1),(2)の問いに答えなさい。
(1) 正六角形 \( ABCDEF \) の周の長さを \( L \) とします。このとき,\( L \) の値を求めなさい。また,\( \sqrt{3}=1.732 \) として,\( L \) を近似値で表しなさい。
【解答】
\( L=2\sqrt{3} \)
\( L \) の近似値 ・・・ \( 3.464 \)
【解説】
円 \( O \) と辺 \( BC \) の接点を \( P \) とすると,
\( OP⊥BC,OP=\dfrac{1}{2} \) になっています。
\( △OBP \) は \( 30°,60°,90° \) の直角三角形になるので,
\( BP=\dfrac{1}{\sqrt{3}}OP=\dfrac{1}{2\sqrt{3}} \)
\( △OBC \) が正三角形であることから,
点 \( P \) は辺 \( BC \) の中点であり,
\( BC=2BP=\dfrac{1}{\sqrt{3}} \)
正六角形 \( ABCDEF \) の周の長さを \( L \) とするとき,
辺 \( BC \) の長さは \( BC=\dfrac{L}{6} \) と表すことができるので,
\( \dfrac{L}{6}=\dfrac{1}{\sqrt{3}} \)
\( L=\dfrac{6}{\sqrt{3}}=2\sqrt{3} \)
\( \sqrt{3}=1.732 \) とするとき,\( L \) の近似値は
\( L=2\sqrt{3}=2 \times 1.732=3.464 \)
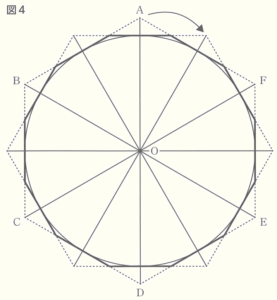
(2) ユウさんとレンさんは図4のように正六角形 \( ABCDEF \) を,点 \( O \) を中心として時計回りの方向に \( 30° \) 回転させた正六角形と,もとの正六角形 \( ABCDEF \) の各辺の交点によってできる正十二角形の周の長さを利用すると,円周率の値により近い値を求めることができると考えました。図4の正十二角形の周の長さを \( M \) とするとき,\( M \) の値を求めなさい。また,\( \sqrt{3}=1.732 \) として,\( M \) を近似値で表しなさい。ただし,求め方や計算過程も書きなさい。
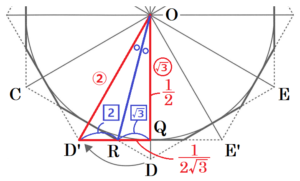
【解答】
正六角形 \( ABCDEF \) を,時計回りに回転させた正六角形の
点 \( D \) が移動した後の点を \( D’ \),点 \( E \) が移動した後の点を \( E’ \) ,
線分 \( OD \) と線分 \( D’E’ \) の交点を点 \( Q \),
線分 \( CD \) と線分 \( D’E’ \) の交点を点 \( R \),
とすると,
\( △OD’Q \) は \( 30°,60°,90° \) の直角三角形になるので,\( OQ=\dfrac{1}{2} \) より,
\( D’Q=\dfrac{1}{\sqrt{3}}OQ=\dfrac{1}{2\sqrt{3}} \)
また,\( ∠QOR=15° \) になるので,線分 \( OR \) は \( ∠D’OQ \) の二等分線であり,
\( D’R:RQ=OD’:OQ=2:\sqrt{3} \)
ここから,
\( RQ=\dfrac{\sqrt{3}}{2+\sqrt{3}}D’Q \)
\( =\dfrac{\sqrt{3}}{2+\sqrt{3}} \times \dfrac{1}{2\sqrt{3}} \)
\( =\dfrac{1}{2(2+\sqrt{3})} \)
\( =\dfrac{2-\sqrt{3}}{2(2+\sqrt{3})(2-\sqrt{3})} \)
\( =\dfrac{2-\sqrt{3}}{2} \)
正十二角形の1辺の長さは \( 2RQ \) であり,\( \dfrac{M}{12} \) と表すこともできるので,
\( \dfrac{M}{12}=2RQ \)
\( \dfrac{M}{12}=2 \times \dfrac{2-\sqrt{3}}{2} \)
\( \underline{M=12(2-\sqrt{3})=24-12\sqrt{3}} \)
\( \sqrt{3}=1.732 \) とするとき,\( M \) の近似値は
\( \underline{M=12(2-\sqrt{3})=12 \times 0.268=3.216} \)
大問6









-300x246.png)