大問１
（１） 次の①～④を計算しなさい。
➀ \( 3-7-(-8) \)
➁ \( -2^2 \times (-3)+6 \)
➂ \( 3a^2b \times 4b \div (-6a) \)
➃ \( \sqrt{2} \times \sqrt{6}+\dfrac{6}{\sqrt{3}} \)
（２） １辺が \( a \; cm \) の正方形を底面とし，高さが \( b \; cm \) である正四角柱の体積が \( 20 \; cm^3 \) であった。このとき，\( b \) を \( a \) の式で表しなさい。
（３） ２次方程式 \( 3x^2-12=0 \) を解きなさい。
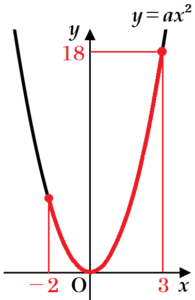
（４） 関数 \( y=ax^2 \) について，\( x \) の変域が \( -2≦x≦3 \) のとき，\( y \) の変域は \( 0≦y≦18 \) である。このときの \( a \) の値を求めなさい。
\( y \) の変域は \( 0≦y≦18 \) であることから，
\( a>0 \) であることがわかります。
\( y=ax^2 \;\; (a>0) \) において，
\( x \) の絶対値が最も大きいとき，\( y \) は最大値をとります。
\( -2≦x≦3 \) の範囲において，
絶対値が最も大きいのは \( x=3 \) のときなので，
\( x=3 \) のとき，\( y=18 \) になります。
よって，\( y=ax^2 \) に \( x=3，y=18 \) を代入すると，
\( 18=a \times 3^2 \)
\( a=2 \)
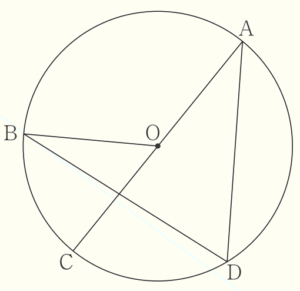
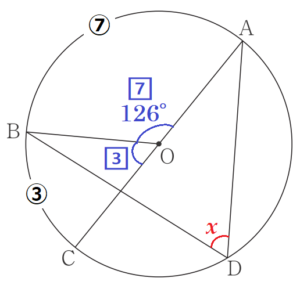
（５） 次の図のように，線分 \( AC \) を直径とする円 \( O \) があり，弧 \( AB： \) 弧 \( BC=7：3 \) とする。このとき，\( ∠ADB \) の大きさは何度か。
中心角と弧の長さは比例するので，
\( ∠AOB：∠COB= \) 弧 \( AB： \) 弧 \( BC=7：3 \)
であり，線分 \( AC \) が直径であることから，
\( ∠AOB=180° \times \dfrac{7}{10}=126° \)
\( ∠ADB \) は弧 \( AB \) の円周角，
\( ∠AOB \) は弧 \( AB \) の中心角なので，
\( ∠ADB=\dfrac{1}{2}∠AOB=63° \)
（６） １から６までの目が出る２つのさいころＡ，Ｂを同時に投げるとき，さいころＡの出た目の数を \( a \)，さいころＢの出た目の数を \( b \) とする。このとき，\( a+b-1 \) が素数となる確率を求めなさい。ただし，さいころはどの目が出ることも同様に確からしいとする。
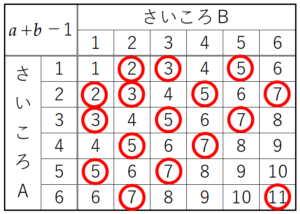
さいころＡ，Ｂの出た目の組み合わせと
\( a+b-1 \) の値を表に書き出すと，
\( 1≦a+b-1≦11 \) になっています。
\( 1≦a+b-1≦11 \) における素数は
\( 2，3，5，7，11 \) であり，
素数になる組み合わせは１６通り，
すべての組み合わせは３６通りなので，
求める確率は \( \dfrac{16}{36}=\dfrac{4}{9} \)
大問２
次の図は，Ａ市の２０２３年と１９７３年の，７月１日から７月３１日までの毎日の最高気温のデータを，それぞれ箱ひげ図で表したものである。このとき，下の（１），（２）の問いに答えなさい。
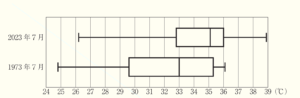
（１） 次の表は，１９７３年７月の毎日の最高気温の四分位数と最大値，最小値をまとめたものである。この表の値をもとに，１９７３年７月の毎日の最高気温の範囲を求めなさい。
（２） 上の箱ひげ図からわかることとして適切なものはどれか。次のア～エからすべて選び，その記号を書きなさい。ただし，猛暑日とは最高気温が \( 35.0 \, ^\circ C \) 以上の日のことをいう。
ア ２０２３年７月は, 半数を超える日が猛暑日である。
イ １９７３年７月の猛暑日の日数は，７日である。
ウ ２０２３年７月と１９７３年７月のどちらにも, 最高気温が \( 33.0 \, ^\circ C \) の日が必ずある。
エ ２０２３年７月の最高気温は，１９７３年７月の最高気温に比べると，\( 2 \, ^\circ C \) 以上高い。
大問３
次の図において，①は関数 \( y=\dfrac{a}{x} \; (a<0) \) のグラフ，②は右上がりの直線である。①と②は２点 \( A，B \) で交わり，点 \( A \) の座標は \( (2，-6) \)，点 \( B \) の座標は \( (12，-1) \) である。また，\( x \) 軸上に \( x \) 座標を \( p \) とする点 \( P \) をとり，２点 \( A，B \) と点 \( P \) を頂点とする三角形 \( ABP \) をつくる。このとき，下の（１）～（３）の問いに答えなさい。
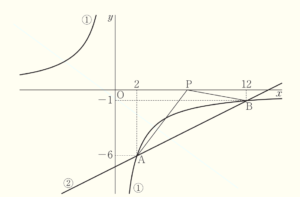
（１） \( a \) の値を求めなさい。
（２） ２点 \( A，B \) を通る直線の式を求めなさい。
（３） 三角形 \( ABP \) の面積が \( 25 \) となる \( p \) の値を求めなさい。ただし，\( 2≦p≦12 \) とする。
\( △ABP \) は，\( △APQ \) と \( △BPQ \) にわかれます。
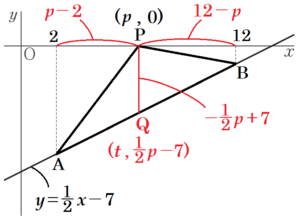
点 \( Q \) は，\( y=\dfrac{1}{2}x-7 \) 上の点で，\( x \) 座標の値は \( p \) なので，
\( Q \left(p，\dfrac{1}{2}p-7 \right) \) であり，
\( PQ \) の長さは，\( PQ=0- \left(\dfrac{1}{2}p-7 \right)=-\dfrac{1}{2}p+7 \)
\( △APQ，△BPQ \) の底辺を \( PQ \) とすると，
\( △APQ \) の高さは，\( p-2 \)，\( △BPQ \) の高さは，\( 12-p \)
と表すことができるので，
\( △APQ+△BPQ= \left(-\dfrac{1}{2}p+7 \right) \times (p-2) \times \dfrac{1}{2}+ \left(-\dfrac{1}{2}p+7 \right) \times (12-p) \times \dfrac{1}{2} \)
\( =\dfrac{1}{2} \left(-\dfrac{1}{2}p+7 \right)\{(p-2)+(12-p)\} \)
\( =\dfrac{1}{2} \left(-\dfrac{1}{2}p+7 \right) \times 10 \)
\( =5 \left(-\dfrac{1}{2}p+7 \right) \)
よって，\( △ABP=△APQ+△BPQ=25 \) のとき，
\( 5 \left(-\dfrac{1}{2}p+7 \right)=25 \)
\( -\dfrac{1}{2}p+7=5 \)
\( p=4 \)
大問４
ゆいさんたちの学級では，数学の授業で次の〔問題〕に取り組んだ。下の 【ゆいさんのノート】と【なぎさんのノート】 は，ゆいさんとなぎさんがこの問題を正しく解いたノートの一部である。このことについて，下の（１），（２） の問いに答えなさい。
〔問題〕
ある中学校の昨年度の全校生徒数は，男女あわせて \( 250 \) 人であった。今年度は，昨年度と比べると，男子の生徒数は \( 20 \; \% \) 増え，女子の生徒数は \( 10 \; \% \) 減り，全校生徒数は \( 11 \) 人増えた。今年度の男子の生徒数を求めなさい。
〔解答〕
昨年度の男子の生徒数を \( x \) 人とすると，昨年度の女子の生徒数は，\( x \) を使って( ア )人と表すことができる。
よって，今年度の全校生徒数について方程式をつくると
イ \( + \) ウ \( ( \) ア \( )=250+11 \)
〔解答〕
昨年度の男子の生徒数を \( x \) 人，昨年度の女子の生徒数を \( y \) 人とする。
昨年度の全校生徒数が \( 250 \) 人であること，今年度の全校生徒数が \( 11 \) 人増加したことについて，それぞれ方程式をつくると
\( \left\{ \begin{array}{}
x+y=250 \\
\;\;\;\; エ \;\;\;\; =11 \\
\end{array} \right. \)
（１） ア ， イ ， エ に当てはまる文字式と， ウ に当てはまる数字を，それぞれ書きなさい。
（２） 今年度の男子の生徒数を求めなさい。
