大問１
（１） 次の①～④を計算しなさい。
① \( -5+6+(-2) \)
➁ \( 8-12 \div (-2)^2 \)
➂ \( 8a \div (-4b^2) \times 3ab^2 \)
④ \( \dfrac{4}{\sqrt{2}}+\sqrt{10} \times \sqrt{5} \)
（２） １個 \( a \; kg \) の荷物 \( 6 \) 個と，１個 \( b \; kg \) の荷物 \( 3 \) 個を合わせた荷物全体の重さは \( 45 \; kg \) であった。このとき，\( b \) を \( a \) の式で表しなさい。
（３） ２次方程式 \( x^2+8x+15=0 \) を解きなさい。
（４） 関数 \( y=-2x+6 \) のグラフについて述べた文として正しいものを，次のア～エからすべて選び，その記号を書きなさい。
ア \( x \) の値が増加すると，\( y \) の値は減少する。
イ 点 \( (-2，6) \) を通る直線である。
ウ グラフの傾きは \( 6 \) である。
エ 方程式 \( 2x+y-6=0 \) のグラフと一致する。
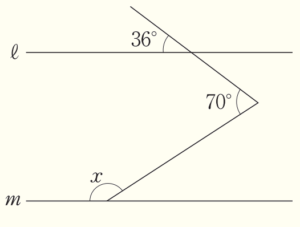
（５） 下の図において，ℓ\( //m \) のとき，\( ∠x \) の大きさは何度か，求めなさい。
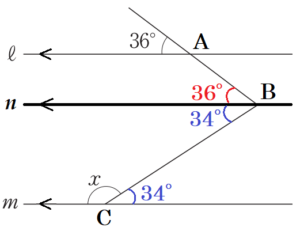
右の図のように点 \( A，B，C \) と名前をつけます。
点 \( B \) を通り，直線 ℓ，\( m \) と平行な直線を \( n \) と
すると，\( ∠B \) の \( 70° \) の角は２つの角に分かれます。
ℓ\( //n \) より，同位角は等しいので，
\( ∠B \) の上側の角は \( 36° \) であり，
下側の角は \( 70°-36°=34° \) になっています。
\( n//m \) より，錯角は等しいので，
\( ∠C \) の小さい方の角は \( 34° \) であり，
\( ∠x=180°-34°=146° \)
（６） ある工場で同じ製品を \( 32000 \) 個作った。この製品のうち，\( 10 \% \) にあたる製品を無作為に抽出して調べたところ，その中に \( 8 \) 個の不良品が見つかった。この工場で作られた \( 32000 \) 個の製品の中に含まれる不良品は，およそ何個あると考えられるか，求めなさい。
大問２
図書委員のりなさんは，中学３年生の１週間の読書時間を調べるために，３年生全体の生徒 \( 50 \) 人に対して，アンケートをとった。このうち，自分の学級の生徒 \( 25 \) 人の結果を，次の【記録】のように，読書時間が短い順に並べかえた後，相対度数を含めた【度数分布表Ａ】に整理しようとしている。このとき，下の（１）・（２）の問いに答えなさい。
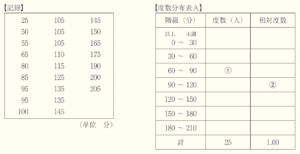
（１） 【度数分布表Ａ】の①・②に当てはまる数をそれぞれ求めなさい。
② ･･･ ある階級の相対度数は，「その階級の度数 \( \div \) 全ての階級の度数の合計」で求められます。
【記録】から，\( 90 \) 分以上 \( 120 \) 分未満の階級の度数は \( 8 \) 人で，
全ての階級の度数の合計は \( 25 \) 人なので，\( 90 \) 分以上 \( 120 \) 分未満の階級の相対度数は
\( 8 \div 25=0.32 \)
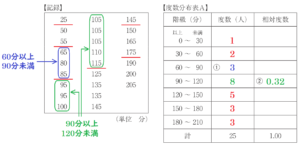
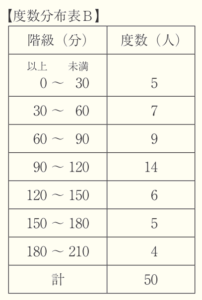
（２） りなさんは，３年生全体の生徒 \( 50 \) 人の結果を右の【度数分布表Ｂ】に整理した。このとき，読書時間が \( 150 \) 分未満の生徒数の割合は，３年生全体の何 \( \% \) か，求めなさい。
また，りなさんの学級は，３年生全体と比べて，読書時間が \( 150 \) 分未満の生徒数の割合が大きいか，小さいか，次のア・イから１つ選び，その記号を書きなさい。
ア りなさんの学級は，３年生全体と比べて，読書時間が \( 150 \) 分未満の生徒数の割合が大きい。
イ りなさんの学級は，３年生全体と比べて, 読書時間が \( 150 \) 分未満の生徒数の割合が小さい。
大問３
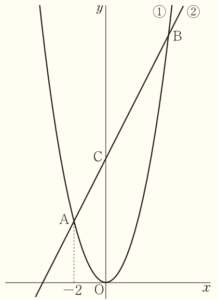
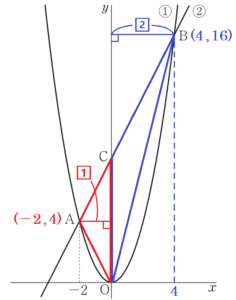
下の図において，①は関数 \( y=x^2 \) のグラフ，②は右上がりの直線である。①と②は２点 \( A，B \) で交わり，点 \( A \) の \( x \) 座標は \( -2 \) である。また，②と \( y \) 軸との交点を \( C \) とする。このとき，次の（１）・（２）の問いに答えなさい。
（１） 点 \( A \) の座標を求めなさい。
（２） 三角形 \( AOC \) と三角形 \( COB \) の面積の比が \( 1：2 \) であるとき，２点 \( A，B \) を通る直線の式を求めなさい。
\( △AOC \) と \( △COB \) は辺 \( OC \) が共通なので，
辺 \( OC \) を底辺とすると，面積の比が \( 1：2 \) であるとき，
高さの比が \( 1：2 \) になります。
\( △AOC \) の高さは，\( 2 \) なので，
\( △COB \) の高さは，その２倍の \( 4 \) であり，
点 \( B \) の \( x \) 座標は \( 4 \) になります。
点 \( B \) は \( y=x^2 \) 上の点で，\( x \) 座標は \( 4 \) なので，
\( y \) 座標は，
\( y=4^2=16 \)
２点 \( A(-2，4)，B(4，16) \) を通る直線の式を \( y=ax+b \) とすると，
\( a=\dfrac{16-4}{4-(-2)}=2 \)
\( y=2x+b \) に \( x=4，y=16 \) を代入すると，
\( 16=2 \times 4+b \)
\( b=8 \)
よって，求める直線の式は \( y=2x+8 \)
大問４
あさひさんは，次の【ルール】にしたがって数を並べたとき，並べた数にはどんなきまりがあるかを考えた。このことについて，下の（１）・（２）の問いに答えなさい。
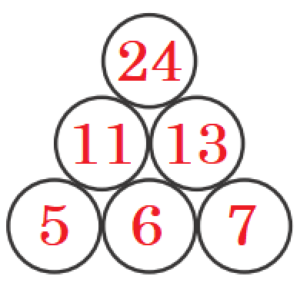
図１のように，６つの○が並べられている。最初に，図１の１段目の３つの○の中に，連続する整数を左から小さい順に書く。次に，２段目の２つの○の中に，１段目の隣り合う整数の和をそれぞれ書く。最後に，３段目の○の中に，２段目の整数の和を書く。図２は１段目の左端の○の中に「\( 2 \)」を書いた場合の例である。
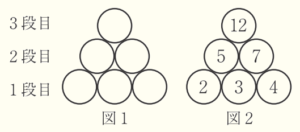
（１） １段目の左端の○の中に「\( 5 \)」を書いたとき，○の中に書いた６つの整数の和を求めなさい。
１段目の左端の○の中に「\( 5 \)」を書いたとき，
残りの○の中の数は右の図のようになるので，
これらの６つの整数の和は，
\( 5+6+7+11+13+24=66 \)
になります。
（２） あさひさんは，１段目の○の中に書く整数を変えながら，２段目，３段目の○の中に入る整数を書き入れていった。○の中の整数を見て，あさひさんは，３段目の整数は，１段目の真ん中の整数の４倍になるのではないかと予想し，n を用いた文字式を使って説明してみようと考えた。次の【あさひさんのノート】は，あさひさんの予想がいつでも成り立つことを，文字を使って正しく説明したノートの一部である。このとき，下の①・②の問いに答えなさい。
【あさひさんのノート】
［予想したことの説明］
１段目の真ん中の整数を \( n \) とすると，１段目に並ぶ連続する３つの
整数は左から小さい順に，
ア ，\( n \)， イ
と表される。
このとき，２段目の整数は１段目の隣り合う整数の和であるから，
左から順に，
ア \( +n= \) ウ ，\( n+ \) イ \( = \) エ
となる。
また，３段目の整数は２段目の整数の和であるから，
ウ \( + \) エ \( = \) オ
となる。
したがって，３段目の整数は，１段目の真ん中の整数の４倍になる。
\( \phantom{ } \)
\( \phantom{ } \)
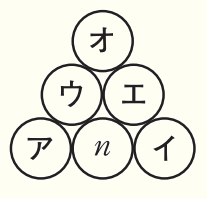
➀ ア ～ オ に当てはまる文字式を，それぞれ書きなさい。
➁ ３段目の整数が \( 620 \) であるとき，１段目の左端の整数を求めなさい。
