大問1
(1) \( \dfrac{1}{7}+\dfrac{1}{2} \)
【解説】
\( =\dfrac{2}{7 \times 2}+\dfrac{7}{2 \times 7} \)
\( =\dfrac{9}{14} \)
(2) \( 6+4 \times (-3) \)
【解説】
\( =6+(-12) \)
\( =-6 \)
(3) \( 8x+9y+7(x-y) \)
【解説】
\( =8x+9y+7x-7y \)
\( =15x+2y \)
(4) \( 8a^3b \div (-6ab)^2 \times 9b \)
【解説】
\( =\dfrac{8a^3b \times 9b}{(-6ab)^2} \)
\( =\dfrac{8a^3b \times 9b}{36a^2b^2} \)
\( =2a \)
(5) \( (x+1)(x-5)+(x+2)^2 \)
【解説】
\( =(x^2-4x-5)+(x^2+4x+4) \)
\( =2x^2-1 \)
(6) \( \sqrt{30} \div \sqrt{5}+\sqrt{54} \)
【解説】
\( =\sqrt{30} \div \sqrt{5}+\sqrt{54} \)
\( =\dfrac{\sqrt{5} \times \sqrt{6}}{\sqrt{5}}+3\sqrt{6} \)
\( =\sqrt{6}+3\sqrt{6} \)
\( =4\sqrt{6} \)
大問2
(1) 一次方程式 \( 5x+8=3x-4 \) を解きなさい。
【解説】
\( 5x-3x=-4-8 \)
\( 2x=-12 \)
\( x=-6 \)
(2) 二次方程式 \( 2x^2+5x-1=0 \) を解きなさい。
【解答】
\( x=\dfrac{-5±\sqrt{33}}{4} \)
【解説】
\( ax^2+bx+c=0 \) と考えると,\( a=2,b=5,c=-1 \) なので,
解の公式 \( \dfrac{-b±\sqrt{b^2-4ac}}{2a} \) に代入すると,
\( x=\dfrac{-5±\sqrt{5^2-4 \times 2 \times (-1)}}{2 \times 2} \)
\( =\dfrac{-5±\sqrt{25+8}}{4} \)
\( =\dfrac{-5±\sqrt{33}}{4} \)
(3) \( y \) は \( x \) に反比例し,\( x=2 \) のとき \( y=3 \) である。\( x=5 \) のときの \( y \) の値を求めなさい。
【解答】
\( y=\dfrac{6}{5} \)
【解説】
反比例の式は \( y=\dfrac{a}{x} \) (\( a \) は定数)で表されるので,
\( x=2,y=3 \) を代入すると,
\( 3=\dfrac{a}{2} \)
\( a=6 \)
よって,\( y=\dfrac{6}{x} \) に \( x=5 \) を代入すると,
\( y=\dfrac{6}{5} \)
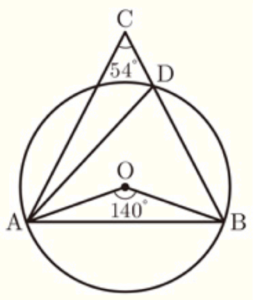
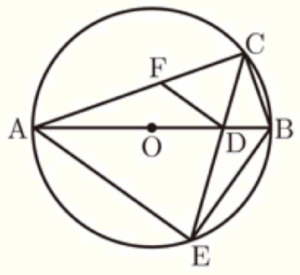
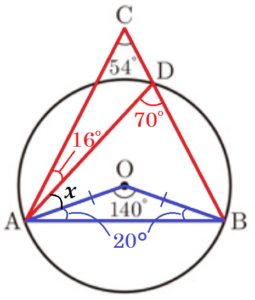
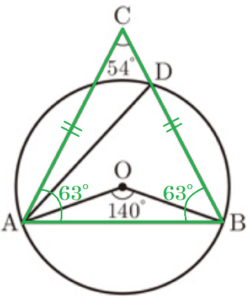
(4) 右の図は,点 \( O \) を中心とする円で,2点 \( A,B \) は円 \( O \) の周上にある。点 \( C \) は円 \( O \) の外部にあり,\( AC=BC \) である。線分 \( BC \) と円 \( O \) との交点のうち,\( B \) と異なる点を \( D \) とする。\( ∠ACB=54°,∠AOB=140° \) であるとき,\( ∠OAD \) の大きさを求めなさい。
【解説】
\( ∠ADB \) は弧 \( AB \) に対する円周角なので,
\( ∠ADB=\dfrac{1}{2}∠AOB=70° \)
\( ∠ADB \) は \( △ACD \) の外角なので,
\( ∠CAD=∠ADB-∠ACD=70-54=16° \)
\( △OAB \) は \( OA=OB \) の二等辺三角形なので,
\( ∠OAB=\dfrac{1}{2}(180-∠AOB)=20° \)
仮定より,\( △ABC \) は二等辺三角形なので,
\( ∠CAB=\dfrac{1}{2}(180-∠ACB)=63° \)
以上より,
\( ∠CAD+∠OAD+∠OAB=∠CAB \)
\( 16+∠OAD+20=63 \)
\( ∠OAD=27° \)
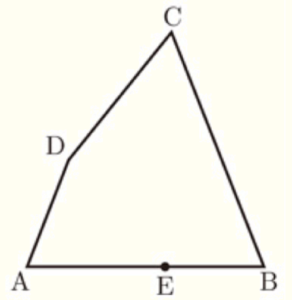
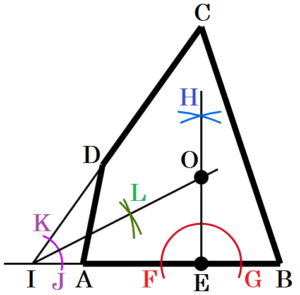
(5) 右の図のように,四角形 \( ABCD \) があり,辺 \( AB \) 上に点 \( E \) がある。点 \( E \) で辺 \( AB \) に接し,辺 \( CD \) にも接する円の中心 \( O \) を,定規とコンバスを使って作図しなさい。なお,作図に用いた線は消さずに残しておくこと。
【解答・解説】
・ 円の半径と接線は接点において垂直に交わる
・ 2本の接線の交点と円の中心を通る直線は,2本の接線が作る角の二等分線になる
の2つの性質を利用して作図します。
手順1 点 \( E \) を中心に弧を描く
(辺 \( AB \) との交点を点 \( F,G \) とします )
手順2 点 \( F,G \) を中心に同じ半径の弧を描く
(交点を点 \( H \) とします )
手順3 点 \( E,H \) を通る直線を描く
手順4 辺 \( AB,CD \) を交わるように延長する
(交点を点 \( I \) とします )
手順5 点 \( I \) を中心に弧を描く
(線分 \( BI,CI \) との交点を点 \( J,K \) とします )
手順6 点 \( J,K \) を中心に同じ半径の弧を描く
(交点を点 \( L \) とします )
手順7 点 \( I,L \) を通る直線を描く
手順3と7の直線の交点が円の中心 \( O \) になります。
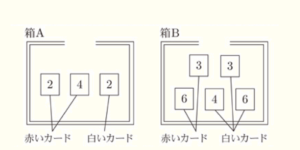
(6) 下の図のように,箱A,箱Bの2つの箱がある。箱Aには \( 2,4 \) の数字が1つずつ書かれた2枚の赤いカードと \( 2 \) の数字が書かれた1枚の白いカードが,箱Bには \( 3,6 \) の数字が1つずつ書かれた2枚の赤いカードと \( 3,4,6 \) の数字が1つずつ書かれた3枚の白いカードが入っている。箱Aと箱Bからそれぞれ1枚ずつカードを取り出し,取り出した2枚のカードを用いて次のように得点を決めることにした。
・取り出した2枚のカードの色が同じときは,その2枚のカードに書かれた数の積を得点とする。
・取り出した2枚のカードの色が異なるときは,その2枚のカードに書かれた数の和を得点とする。
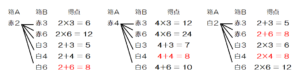
➀ 得点の最大値を求めなさい。
【解説】
取り出した2枚のカードの組み合わせを樹形図で表し,得点を計算します。

➁ 次の ア , イ に当てはまる数を入れて,文を完成しなさい。ただし,どのカードが取り出されることも同様に確からしいものとする。
得点が ア 点となる確率が最も高く,その確率は イ である。
【解答】
ア ・・・ \( 8 \)
イ ・・・ \( \dfrac{4}{15} \)
【解説】
取り出した2枚のカードの組み合わせを樹形図で表し,得点を計算します。
得点が \( 8 \) 点になるときが4通りで最も多く,すべての組み合わせは15通りなので,確率は \( \dfrac{4}{15} \)
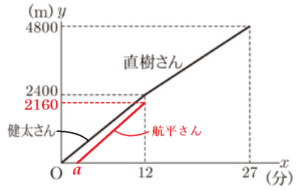
(7) 健太さんと直樹さんは,航平さんと,運動公園にある1周 \( 2400 \; m \) のジョギングコースを走った。
健太さんと直樹さんはスタート地点から1周ずつ,健太さんから直樹さんの順にそれぞれ一定の速さで走った。健太さんは走り始めてから \( 12 \) 分後に1周を走り終え,直樹さんへ引き継いだ。直樹さんは引き継ぎと同時に健太さんと同じ方向に走り始め,引き継ぎから \( 15 \) 分後に1周を走り終えた。
一方,航平さんは一人で2周を走ることとし,健太さんが走り始めて \( a \) 分後に,毎分 \( 240 \; m \) の速さで健太さんと同じスタート地点から健太さんと同じ方向に走り始めた。健太さんが走り終えたとき,航平さんは1周目の途中を走っており,健太さんと \( 240 \; m \) 離れていた。航平さんは2周目の途中で直樹さんを追いこし,その後も毎分 \( 240 \; m \) の速さで \( 2 \) 分以上走ったが,ある地点で \( b \) 分間立ち止まった。航平さんは,直樹さんが航平さんに並ぶと同時に直樹さんと同じ速さで一緒に走り,2周を走り終えた。
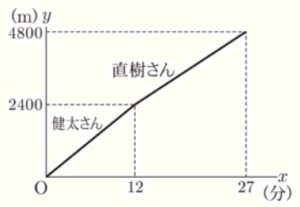
右の図は,健太さんが走り始めてから \( x \) 分後の,健太さんと直樹さんが走った距離の合計を \( y \; m \) として,\( x \) と \( y \) の関係をグラフに表したものである。
➀ \( a \) の値を求めなさい。
【解説】
健太さんが走り終えたとき,
つまり,\( x=12 \) (分)のときまでに
航平さんが走った距離は,
\( y=2400-240=2160 \; (m) \) なので,
航平さんが走った速さは,
毎分 \( \dfrac{2160}{12-a} \; m \) と表すことができます。
よって,
\( \dfrac{2160}{12-a}=240 \)
\( 2160=240(12-a) \)
\( 240a=720 \)
\( a=3 \)
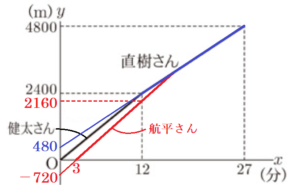
➁ 航平さんが直樹さんと最初に並んだのは,健太さんが走り始めてから何分後か,求めなさい。
【解説】
航平さんが走った状態を表す直線の式を \( y=240x+c \) とすると,この直線は,\( (3,0) \) を通っているので,これを代入すると,
\( 0=240 \times 3+c \)
\( c=-720 \)
よって,航平さんが走った状態を表す直線の式は
\( y=240x-720 \) ・・・ ➀
直樹さんは \( 15 \) 分で \( 2400 \; m \) を走ったので,
直樹さんが走った速さ(傾き)は,
\( \dfrac{2400}{15}=160 \; (m) \)
直樹さんが走った状態を表す直線の式を
\( y=160x+d \) とすると,
この直線は,\( (12,2400) \) を通っているので,
これを代入すると,
\( 2400=160 \times 12+d \)
\( d=480 \)
よって,直樹さんが走った状態を表す直線の式は
\( y=160x+480 \) ・・・ ➁
➀➁を連立方程式として解くと,
\( x=15,y=2880 \)
よって,答えは,\( 15 \) 分後
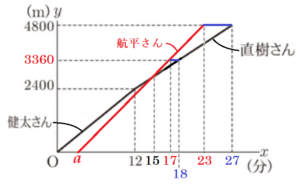
➂ \( b \) の値の範囲を求めなさい。
【解説】
(2) より,航平さんが直樹さんと最初に並んだのは,\( x=15 \) 分のとき
直樹さんを追いこした後も \( 2 \) 分以上走ったので,
少なくとも \( x=17 \) 分までは走ったことになります。
このとき,航平さんが走った距離は,
\( y=240 \times 17-720=3360 \; (m) \)
健太さんと直樹さんが走った距離の合計が \( 3360 \; m \) になる時間を \( x=s \) とすると,
\( 3360=160 \times s+480 \)
\( 160s=2880 \)
\( s=18 \) (分)
なので,航平さんが立ち止まる時間は,
\( b=18-17=1 \) (分)
また,航平さんが2周目を走り終わるときの時間を \( x=t \) とすると,
\( 4800=240 \times t-720 \)
\( 240t=5520=23 \)
\( t=23 \) (分)
健太さんと直樹さんが走った距離の合計が \( 4800 \; m \) になるのは,\( x=27 \) 分のときなので,
このとき,航平さんが立ち止まる時間は,
\( b=27-23=4 \) (分)
2周目を走り終わる前に立ち止まる必要があるので,
\( b \) の値の範囲は,\( 1≦b<4 \)
大問3
次の図は,美咲さんが通う高校の,1年1組39人と1年2組39人の反復横とびの回数の測定結果を,体育委員である美咲さんが箱ひげ図に表したものである。
このとき,次の各問いに答えなさい。
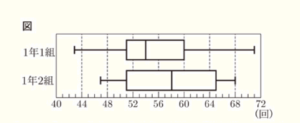
(1) 次の ア , イ に当てはまる数を入れて,文を完成しなさい。
図の1組の箱ひげ図から,回数の範囲は ア 回,四分位範囲は イ 回であることがわかる。
【解答】
ア ・・・ \( 28 \)
イ ・・・ \( 9 \)
【解説】
ア ・・・ 範囲 \( = \) 最大値 \( – \) 最小値 \( =71-43=28 \) (回)
イ ・・・ 四分位範囲 \( = \) 第三四分位数 \( – \) 第一四分位数 \( =60-51=9 \) (回)
さらに美咲さんは,その測定結果をヒストグラムに表した。
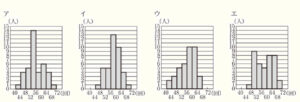
(2) 次のア〜エのヒストグラムのうち,1組と2組を表しているものはどれか。それぞれ記号で答えなさい。
なお,ヒストグラムの階級は,40回以上44回未満,44回以上48回未満などのように,階級の幅を4回として分けている。
【解説】
箱ひげ図から,1組は40回以上44回未満の階級の生徒がいるが,2組にはいないので,
1組のヒストグラムは,アまたはウ,2組のヒストグラムは,イまたはエ であるとわかります。
1組 ・・・ 1組は68回以上72回未満の階級の生徒がいるので,あてはまるのはア
2組 ・・・ クラス全体の人数が39人なので,第三四分位数(65回)にあたるのは,
回数が多い方から10番目の生徒の結果なので,
64回以上68回未満,68回以上72回未満の階級の度数が合計10人以上になります。
よって,あてはまるのはエ
(3) 美咲さんと同じ体育委員の大輔さん,由衣さん,雄太さん,恵子さんは,箱ひげ図やヒストグラムから読みとれることについて,それぞれ次のように考えた。
大輔さん:回数の範囲は,1組よりも2組の方が大きい。
由衣さん:回数の四分位範囲は,1組よりも2組の方が大きい。
雄太さん:回数が64回以上である人数は,1組よりも2組の方が多い。
恵子さん:1組の回数の平均値は,60回である。
4人のうち,正しい読みとりをしているのは誰か。次のア〜エからすべて選び,記号で答えなさい。
ア 大輔さん イ 由衣さん ウ 雄太さん エ 恵子さん
【解説】
大輔さん:箱ひげ図から,1組の範囲 \( =71-43=28 \) (回),2組の範囲 \( =68-47=21 \) (回)
由衣さん:箱ひげ図から,
1組の四分位範囲 \( =60-51=9 \) (回)
2組の四分位範囲 \( =65-51=14 \) (回)
雄太さん:(2)から,1組のヒストグラムはア,2組のヒストグラムはエなので,
回数が64回以上である人数は,1組が5人,2組が10人
恵子さん:ヒストグラムから,60回以上の階級の度数の合計が11人であるのに対して,
52回以上56回未満の階級だけでも14人いるので,平均値は明らかに60回未満になる。
大問4
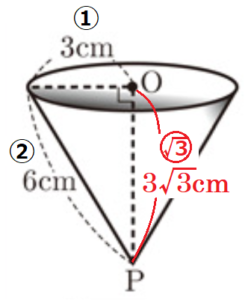
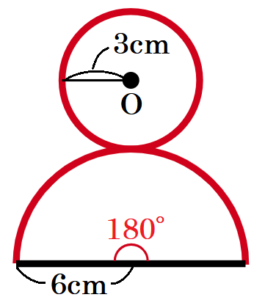
図1は,底面の半径が \( 3 \; cm \) ,母線の長さが \( 6 \; cm \) の円すいの形をした容器Aである。底面の円の中心を \( O \) ,頂点を \( P \) とすると,底面と線分 \( OP \) は垂直に交わっている。図1の容器Aに球Bを,容器Aの内側の面にぴったりつくように入れたところ,図2のように球Bの中心が \( O \) と重なった。図3は,図2の立面図である。
このとき,次の各問いに答えなさい。ただし,円周率は \( \pi{} \) とし,容器Aの厚さは考えないものとする。また,根号がつくときは,根号のついたままで答えること。
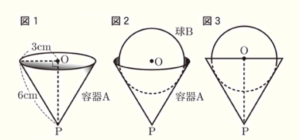
(1) 容器Aの容積を求めなさい。
【解答】
\( 9\sqrt{3}\pi{} \; cm^3 \)
【解説】
容器Aを正面から見たとき,半分の三角形が
短辺と斜辺の比が \( 1:2 \) の直角三角形になっているので,
高さ \( OP \) の比は \( \sqrt{3} \) になります。
\( OP:3=\sqrt{3}:1 \)
\( OP=3\sqrt{3} \; (cm) \)
よって,容器Aの容積は,
\( \pi{} \times 3^2 \times 9\sqrt{3} \times \dfrac{1}{3}=9\sqrt{3}\pi{} \; (cm^3) \)
(2) 容器Aの側面積を求めなさい。
【解答】
\( 18\pi{} \; cm^2 \)
【解説】
容器Aの展開図を考えると,
円 \( O \) の周と側面を展開したおうぎ形の弧はぴったり重なっていたので,長さは等しくなっています。
おうぎ形の中心角を \( x° \) とすると,
\( 2\pi{} \times 3=2\pi{} \times 6 \times \dfrac{x}{360} \)
\( \dfrac{1}{2}=\dfrac{x}{360} \)
\( x=180 \)
なので,このおうぎ形は半円になっています。
よって,側面席は,
\( \pi{} \times 6^2 \times \dfrac{180}{360}=18\pi{} \; (cm^2) \)
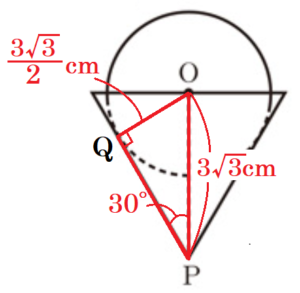
(3) 球Bの半径を求めなさい。
【解答】
\( \dfrac{3\sqrt{3}}{2} \; cm \)
【解説】
図3における容器Aと球Bの接点を点 \( Q \) とすると,
\( OQ \) が球Bの半径になります。
(1) より,容器Aを正面から見たとき,半分の三角形は \( 1:2: \sqrt{3} \) の直角三角形なので, \( ∠OPQ=30° \)
また,\( △OPQ \) も \( 30°,60°,90° \) の直角三角形なので,
\( OQ=\dfrac{1}{2}OP=\dfrac{3\sqrt{3}}{2} \; (cm) \)
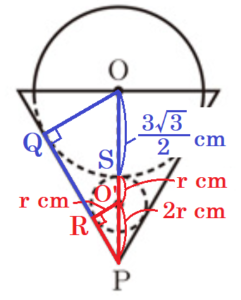
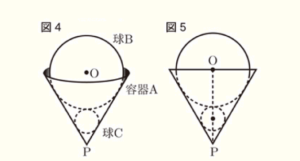
(4) 図4のように,容器Aと球Bの間にちょうど入るような球Cを入れた。図5は,図4の立面図である。球Cの体積を求めなさい。
【解答】
\( \dfrac{\sqrt{3}}{2}\pi{} \; cm^3 \)
【解説】
球Cの中心を \( O’ \),容器Aと球Cの接点を点 \( R \),
球Cの半径を \( r \; cm \) とすると,
\( △O’PR \) も \( 30°,60°,90° \) の直角三角形なので,
\( O’P=2r \; cm \) となります。
また,球Bと球Cの接点を点 \( S \) とすると,
\( OS \) は球Bの半径になっているので,\( OS=\dfrac{3\sqrt{3}}{2} \; cm \)
\( O’S \) は球Cの半径になっているので,\( O’S=r \; cm \)
(1) より,\( OP=3\sqrt{3} cm \) なので,
\( OP=OS+O’S+O’P \)
\( 3\sqrt{3}=\dfrac{3\sqrt{3}}{2}+r+2r \)
\( 3r=\dfrac{3\sqrt{3}}{2} \)
\( r=\dfrac{\sqrt{3}}{2} \; (cm) \)
よって,球Cの体積は,
\( \dfrac{4\pi{}}{3} \times \left(\dfrac{\sqrt{3}}{2} \right)^3=\dfrac{\sqrt{3}}{2}\pi{} \; (cm^3) \)
大問5
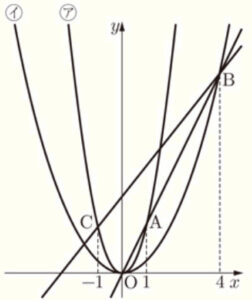
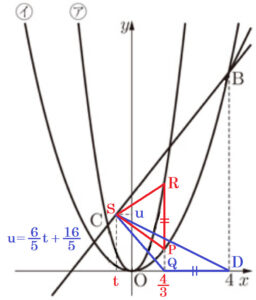
右の図のように,2つの関数 \( y=2x^2 \) ・・・ ア,\( y=ax^2 \) (\( a \) は定数) ・・・ イ のグラフがある。
点 \( A \) は関数 ア のグラフ上にあり,\( x \) 座標は \( 1 \) である。点 \( B \) は関数 イ のグラフ上にあり,\( x \) 座標が \( 4 \) で,直線 \( AB \) は原点 \( O \) を通る。また,点 \( C \) は関数 ア のグラフ上にあり,\( x \) 座標は \( -1 \) である。
このとき,次の各問いに答えなさい。
(1) \( a \) の値を求めなさい。
【解答】
\( a=\dfrac{1}{2} \)
【解説】
点 \( A \) は,\( y=2x^2 \) 上の点なので,
\( x=1 \) を代入すると,\( y=2 \times 1^2=2 \)
よって, \( A \) の座標は,\( A(1,2) \)
直線 \( AB \) は原点 \( O \) と \( A(1,2) \) を通るので,この直線の式は \( y=2x \)
ここに \( x=4 \) を代入すると,\( y=2 \times 4=8 \)
よって, \( B \) の座標は,\( B(4,8) \)
\( y=ax^2 \) に \( x=4,y=8 \) を代入すると,
\( 8=a \times 4^2 \)
\( a=\dfrac{1}{2} \)
(2) 直線 \( BC \) の式を求めなさい。
【解答】
\( y=\dfrac{6}{5}x+\dfrac{16}{5} \)
【解説】
点 \( C \) は,\( y=2x^2 \) 上の点なので,
\( x=-1 \) を代入すると,\( y=2 \times (-1)^2=2 \)
よって, \( C \) の座標は,\( C(-1,2) \)
直線 \( BC \) は \( C(-1,2) \) と \( B(4,8) \) を通るので,
傾き \( =\dfrac{8-2}{4-(-1)}=\dfrac{6}{5} \)
求める式を \( y=\dfrac{6}{5}x+b \) とし,\( x=-1,y=2 \) を代入すると,
\( 2=\dfrac{6}{5} \times (-1)+b \)
\( b=\dfrac{16}{5} \)
よって,直線 \( BC \) の式は,\( y=\dfrac{6}{5}x+\dfrac{16}{5} \)
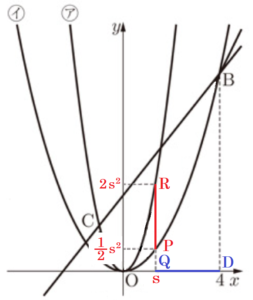
(3) 点 \( B \) から \( x \) 軸にひいた垂線と \( x \) 軸との交点を \( D \) ,直線 \( BC \) と \( y \) 軸との交点を \( E \) とする。関数 イ のグラフ上において2点 \( O,B \) の間に点 \( P \) をとり,点 \( P \) から \( x \) 軸にひいた垂線と \( x \) 軸との交点を \( Q \) とする。また,直線 \( PQ \) と関数 ア のグラフとの交点を \( R \) とする。
\( PR=QD \) のとき,
① 点 \( P \) の \( x \) 座標を求めなさい。
【解説】
点 \( P \) の \( x \) 座標を \( s \) とすると,
\( y \) 座標は,\( \dfrac{1}{2}s^2 \) と表すことができます。
また,点 \( Q,R \) の \( x \) 座標も \( s \) になるので,
点 \( R \) の \( y \) 座標は,\( 2s^2 \) と表すことができます。
このとき,\( PR \) の長さは,\( PR=2s^2-\dfrac{1}{2}s^2=\dfrac{3}{2}s^2 \)
\( QD \) の長さは,\( QD=4-s \) と表すことができるので,
\( PR=QD \)
\( \dfrac{3}{2}s^2=4-s \)
\( 3s^2=8-2s \)
\( 3s^2+2s-8=0 \)
\( (3s-4)(s+2)=0 \)
\( s=\dfrac{4}{3} \) (\( s>0 \)より)
➁ 線分 \( CE \) 上に点 \( S \) をとる。\( △SPR \) の面積が,\( △SQD \) の面積の \( \dfrac{5}{6} \) 倍となるときの \( S \) の座標を求めなさい。
【解答】
\( S\left( -\dfrac{2}{3},\dfrac{12}{5} \right) \)
【解説】
問題の条件より,\( PR=QD \) なので,
\( △SPR \) の底辺を \( PR \),\( △SQD \) の底辺を \( QD \) とすると,
\( △SPR \) の高さが \( △SQD \) の高さの \( \dfrac{5}{6} \) 倍 になるとき,
\( △SPR \) の面積が,\( △SQD \) の面積の \( \dfrac{5}{6} \) 倍となります。
点 \( S \) は直線 \( BC \) 上の点なので,\( x \) 座標を \( t \) とすると,
\( y \) 座標は \( \dfrac{6}{5}t+\dfrac{16}{5} \) と表すことができます。
このとき,
\( △SPR \) の高さは,\( \dfrac{4}{3}-t \),
\( △SQD \) の高さは,\( \dfrac{6}{5}t+\dfrac{16}{5} \)
と表すことができます。
よって,
\( \dfrac{4}{3}-t=\dfrac{5}{6} \left( \dfrac{6}{5}t+\dfrac{16}{5} \right) \)
\( \dfrac{4}{3}-t=t+\dfrac{8}{3} \)
\( 2t=-\dfrac{4}{3} \)
\( t=-\dfrac{2}{3} \)
\( \dfrac{6}{5}t+\dfrac{16}{5} \) に代入すると,
\( \dfrac{6}{5} \times \left( -\dfrac{2}{3} \right) +\dfrac{16}{5}=\dfrac{12}{5} \)
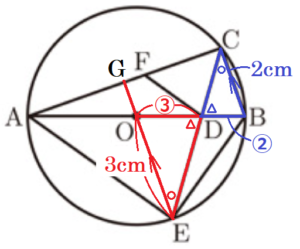
大問6
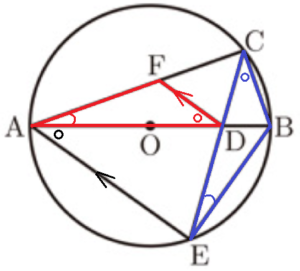
右の図は,点 \( O \) を中心とする円で,線分 \( AB \) は円の直径である。弧 \( AB \) 上に点 \( C \) を,\( AC>BC \) となるようにとる。点 \( D \) は線分 \( OB \) 上にあり,点 \( E \) は \( CD \) の延長と \( C \) を含まない弧 \( AB \) との交点である。また,点 \( F \) は線分 \( AC \) 上にあって,\( FD//AE \) である。
このとき,次の各問いに答えなさい。ただし,根号がつくときは,根号のついたままで答えること。
(1) \( △ADF \) ∽ \( △ECB \) であることを証明しなさい。
【解説】
\( △ADF \) と \( △ECB \) において,
弧 \( BC \) に対する円周角なので,\( ∠FAD=∠BEC \) ・・・ ➀
\( FD//AE \) より,錯角は等しいので,\( ∠FDA=∠DAE \) ・・・ ➁
弧 \( BE \) に対する円周角なので,\( ∠DAE=∠BCE \) ・・・ ➂
➁➂より,\( ∠FDA=∠BCE \) ・・・ ④
➀④より,2組の角がそれぞれ等しいので,
\( △ADF \) ∽ \( △ECB \)
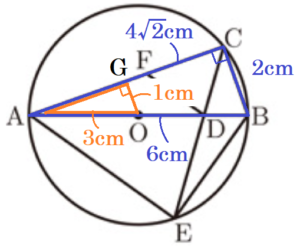
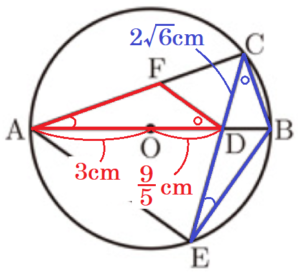
(2) \( AB=6 \; cm,BC=2 \; cm,AE=CE \) のとき,
➀ 線分 \( AE \) の長さを求めなさい。
【解答】
\( 2\sqrt{6} \; cm \)
【解説】
点 \( E \) から線分 \( AC \) に垂線をひき,交点を点 \( G \) とすると,
直角三角形 \(AEG\) ができるので,三平方の定理を使って線分 \( AE \) の長さを求めます。
\( △ABC \) は直角三角形,\( AB=6 \; cm,BC=2 \; cm \) なので,
三平方の定理より,
\( AC^2=AB^2-BC^2 \)
\( =6^2-2^2 \)
\( =32 \)
\( AC=4\sqrt{2} \; (cm) \) (\( AC>0 \)より)
また,\( △AOG \) ∽ \( △ABC \) なので,
\( AO:AB=OG:BC \)
\( 3:6=OG:2 \)
\( OG=1 \; (cm) \)
\( AE=CE,AC⊥EG \) より,\( AG=\dfrac{1}{2}AC \) なので,
\( AG=\dfrac{1}{2} \times 4\sqrt{2}=2\sqrt{2} \; (cm) \)
また,\( EG=EO+OG=3+1=4 \; (cm) \)
よって,三平方の定理より,
\( AE^2=AG^2+EG^2 \)
\( =(2\sqrt{2})^2+4^2 \)
\( =24 \)
\( AE=2\sqrt{6} \; (cm) \) (\( AE>0 \)より)
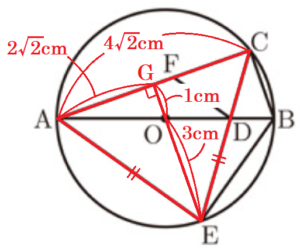
➁ \( △ADF \) の面積は,\( △ECB \) の面積の何倍であるか,求めなさい。
【解答】
\( \dfrac{24}{25} \) 倍
【解説】
(1) より,\( △ADF \)
∽ \( △ECB \) であることがわかっているので,
相似な三角形の面積比は相似比の2乗の比になることを利用して解いていきます。
今回は,\( AE=CE,AE=2\sqrt{6} \; cm \) であることから,
\( AD \) の長さを求めることで解くことができます。
\( EG⊥AC,BC⊥AC \) より,\( EG//BC \)
錯角が等しいので,\( ∠OED=∠BCD \) ・・・ ➀
対頂角は等しいので,\( ∠ODE=∠BDC \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,\( △ODE \) ∽ \( △BDC \)
\( OE=3 \; cm,BC=2 \; cm \) より,
\( OD:BD=OE:BC=3:2 \)
\( OB=3 \; cm \) より,
\( OD=\dfrac{3}{5}OB \)
\( =\dfrac{3}{5} \times 3 \)
\( =\dfrac{9}{5} \; (cm) \)
\( OA=3 \; cm \) なので,
\( AD=OA+OD=3+\dfrac{9}{5}=\dfrac{24}{5} \; (cm) \)
\( AE=CE \) より,
\( EC=AE=2\sqrt{6} \; (cm) \)
(1) より,\( △ADF \) ∽ \( △ECB \) なので,相似比は,
\( AD:EC=\dfrac{24}{5}:2\sqrt{6} \)
\( =24:10\sqrt{6} \)
\( =12:5\sqrt{6} \)
相似な三角形の面積比は相似比の2乗の比になるので,
\( △ADF:△ECB=12^2:(5\sqrt{6})^2 \)
\( =24:25 \)
よって,\( △ADF \) の面積は,\( △ECB \) の面積の \( \dfrac{24}{25} \) 倍