大問1
(1) \( \dfrac{1}{3}-\dfrac{1}{5} \)
【解説】
\( =\dfrac{5}{15}-\dfrac{3}{15} \)
\( =\dfrac{2}{15} \)
(2) \( 2 \times (7-9) \)
【解説】
\( =2 \times (-2) \)
\( =-4 \)
(3) \( 7x+4y-(8x-5y) \)
【解説】
\( =7x+4y-8x+5y \)
\( =-x+9y \)
(4) \( 8a^2b \div (-6ab)^2 \times 9b^3 \)
【解説】
\( =\dfrac{8a^2b \times 9b^3}{(-6ab)^2} \)
\( =\dfrac{72a^2b^4}{36a^2b^2} \)
\( =2b^2 \)
(5) \( (2x-3)^2+2(6x+5) \)
【解説】
\( =(4x^2-12x+9)+12x+10 \)
\( =4x^2+19 \)
(6) \( \sqrt{10}+\sqrt{40} \)
【解説】
\( =\sqrt{10}+2\sqrt{10} \)
\( =3\sqrt{10} \)
大問2
(1) 一次方程式 \( 5x+8=6x-1 \) を解きなさい。
(2) \( 2x^2-18 \) を因数分解しなさい。
【解説】
\( =2(x^2-9) \)
\( =2(x+3)(x-3) \)
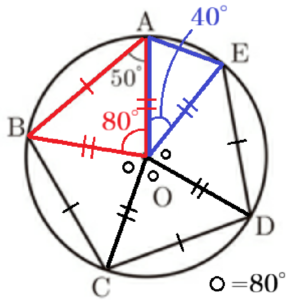
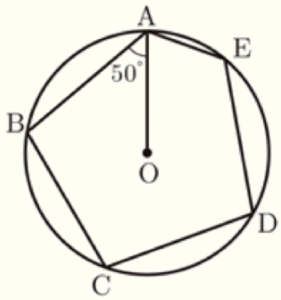
(3) 右の図のように,\( AB=BC=CD=DE \) である五角形 \( ABCDE \) の5つの頂点 \( A,B,C,D,E \) が点 \( O \) を中心とする円の周上にある。
\( ∠OAB=50° \) であるとき,\( ∠OAE \) の大きさを求めなさい。
【解説】
補助線 \( OB \) をひくと,\( △OAB \) は二等辺三角形なので,
\( ∠AOB=180°-50° \times 2=80° \)
さらに,補助線 \( OC,OD,OE \) をひくと,
\( AB=BC=CD=DE \) より \( △OAB,△OBC,△OCD,△ODE, \) は
いずれも3辺の長さが等しく,合同なので,
\( ∠AOB=∠BOC=∠COD=∠DOE=80° \)
であり,
\( ∠AOE=360°-80° \times 4=40° \)
\( △OAE \) も二等辺三角形なので,
\( ∠OAE=\dfrac{180°-40°}{2}=70° \)
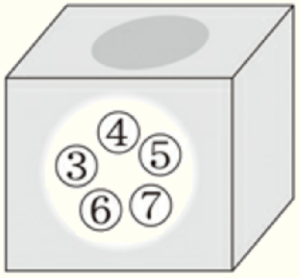
(4) 右の図のように,\( 3,4,5,6,7 \) の数字が1つずつ書かれた5個の玉が入った箱がある。この箱から玉を1個取り出し,取り出した玉に書かれている数を確認してから箱にもどすことを2回行う。
1回目に取り出した玉に書かれている数を \( a \),2回目に取り出した玉に書かれている数を \( b \) とするとき,\( a+b \) の値が \( 24 \) の約数になる確率を求めなさい。ただし,どの玉が取り出されることも同様に確からしいものとする。
【解説】
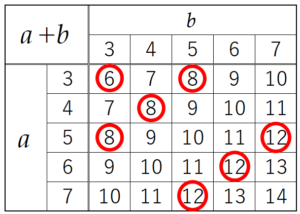
\( a \) と \( b \) の値の組み合わせとそのときの \( a+b \) の値を表に書き出し,\( 24 \) の約数になるところに 〇 を
つけてみます。
\( 24 \) の約数は,\( 1,2,3,4,6,8,12,24 \) なので,あてはまるのは \( 7 \) 通り,
すべての組み合わせは \( 25 \) 通りなので,
求める確率は \( \dfrac{7}{25} \) になります。
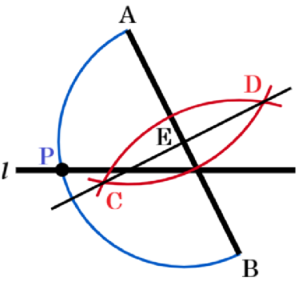
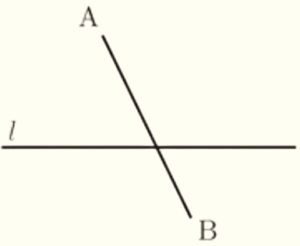
(5) 右の図のように,直線 \( l \) と線分 \( AB \) があり,\( l \) と \( AB \) は交わっている。\( l \) 上に点 \( P \) を,\( ∠APB=90° \) となるようにとりたい。点 \( P \) を,定規とコンパスを使って1つ作図しなさい。なお,作図に用いた線は消さずに残しておくこと。
【解答】
手順1 2点 \( A,B \) を中心に円弧を描く。
(交点を \( C,D \) とします)
手順2 2点 \( C,D \) を通る直線を描く。
(線分 \( AB \) との交点を \( E \) とします。)
手順3 点 \( E \) を中心に線分 \( AE \) を半径とする円弧を描く。
手順3の円弧と直線 \( l \) との交点が求める点 \( P \) になります。
【解説】
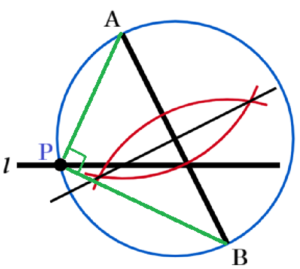
点 \( P \) が線分 \( AB \) を直径とする円周上の点のとき,
\( ∠APB \) は直径 \( AB \) に対する円周角であり,
\( ∠APB=90° \) になります。
線分 \( AB \) が直径であるとき,\( AB \) の中点が円の中心になるので,線分 \( AB \) の垂直二等分線を作図することで,円の中心を求められます。
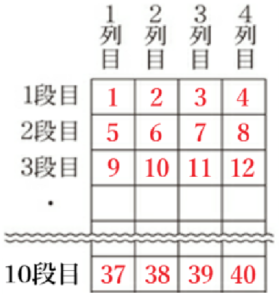
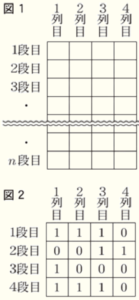
(6) 図1のように,縦に \( n \) 段,横に4列のマス目があり,各マス目に数を1つずつ記入する。記入する数は \( 1,1,1,0,0,0 \) の繰り返しで,1段目の1列目から右方向に数を記入し,各段とも4列目まで記入したら,次の段の1列目に移り,つづけて記入する。
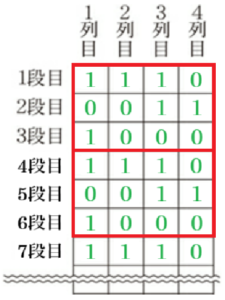
例えば,図2は,\( n=4 \) のときのマス目に数を記入したものである。
1 \( n=10 \) のとき,1段目の1列目から10段目の4列目まで記入したすべての数の和を求めなさい。
【解説】
このマス目において,
1段目に記入する数を1~4番目の数,
2段目に記入する数を5~8番目の数,
と考え,各段の4列目に注目すると,
1段目の4列目は4 \( (=4 \times 1) \) 番目の数,
2段目の4列目は8 \( (=4 \times 2) \) 番目の数,
なので,
10段目の4列目には,40 \( (=4 \times 10) \) 番目の数が記入されます。
次に,【 \( 1,1,1,0,0,0 \) 】 の6個の数の並びを1セットと考えると,
【 \( 1,1,1,0,0,0 \) 】 の数の並び1セットについて,
すべての数の和は \( 3 \) なので,この数の並びが6セット集まったとき,
\( 36(=6 \times 6) \) 番目までの数の和は \( 18(=3 \times 6) \) であり,
10段目に記入される数は,左から順に【 \( 1,1,1,0 \) 】となるので,
10段目の4列目まで記入したすべての数の和は \( 21 \) になります。
2 \( n \) を3の倍数から2引いた自然数とする。1段目の1列目から \( n \) 段目の4列目まで記入したすべての数の和を,\( n \) を使った式で表しなさい。
【解説】
\( n \) が3の倍数から2引いた自然数ということは,
\( n \) 段目は
1 \( (=3 \times 1-2) \) 段目,
4 \( (=3 \times 2-2) \) 段目,
7 \( (=3 \times 3-2) \) 段目,
・・・
になります。
試しに7段目までを表に書き込んでみると,右の図のようになります。
この表で,3段ずつをまとめて考えると,
3段の中に,【 \( 1,1,1,0,0,0 \) 】 の数の並びがちょうど2セット入っているので,和が \( 6 \) になることがわかります。
つまり,
3段目の4列目までの和は \( 6 \),
6段目の4列目までの和は \( 12 \),
9段目の4列目までの和は \( 18 \),
になります。
次に,1段目,4段目,7段目に注目すると,すべて【 \( 1,1,1,0 \) 】になっていて,
1段目だけの和,4段目だけの和,7段目だけの和,はすべて \( 3 \) になっています。
1段目,4段目,7段目,・・・ の並びを1段目,4 \( (=3+1) \) 段目,7 \( (=6+1) \) 段目,・・・ と考えると,
\( n \) 段目の4列目までの和は次のようになります。

よって,この関係を \( n \) を使った式で表すと,\( 2n+1 \) になります。
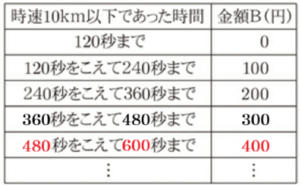
(7) あるタクシー会社の運賃は,タクシーに乗って移動した距離で決まる金額Aと,タクシーの利用中に信号待ちや渋滞など,時速 \( 10 \; km \) 以下であった時間で決まる金額Bとを合計した金額である。タクシーに乗って移動した距離と金額Aの関係は表1のとおりであり,\( 1100 \; m \) をこえると,\( 300 \; m \) ごとに \( 100 \) 円が加算される。また,時速 \( 10 \; km \) 以下であった時間と金額Bの関係は表2のとおりであり,\( 120 \) 秒をこえると,\( 120 \) 秒ごとに \( 100 \) 円が加算される。なお,消費税は考えないものとする。

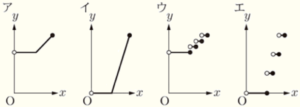
1 この会社のタクシーに乗って \( x \; m \) 移動したときの金額Aを \( y \) 円とする。\( 0<x≦2000 \) のとき,\( x \) と \( y \) の関係を表したグラフとして最も適当なものを,下のア~エから1つ選び,記号で答えなさい。ただし,グラフにおいて,端の点をふくむ場合は ●,ふくまない場合は ○ で表している。
【解説】
タクシーの運賃は,一定の距離をこえると一気に料金が跳ね上がります。
(例えば,この会社の場合,運賃が \(
750 \) 円になることは絶対にありません)
このような変化のしかたを表しているグラフは ウ または エ になります。
エ のグラフは,\( 1100 \; m \) までの料金が \( 0 \) 円になっているので誤りであり,
あてはまるのは ウ のグラフになります。
2 次の P ~ R に当てはまる数を入れて,文章を完成しなさい。
この会社のタクシーに乗って \( 6300 \; m \) 移動したところ,金額Aと金額Bの合計が \( 2900 \) 円であった。
このとき,金額Aは P 円であり,タクシーの利用中に時速 \( 10 \; km \) 以下であった時間は Q 秒を
こえて R 秒までであったことがわかる。
【解答】
P ・・・ \( 2500 \)
Q ・・・ \( 480 \)
R ・・・ \( 600 \)
【解説】
P
\( 6300 \; m \) 移動したときの金額Aについて,
距離によって変動する部分は,\( 8300-1100=5200 \; (m) \) であり,
\( 300 \; m \) ごとに \( 100 \) 円が加算されるので,
\( \dfrac{5200}{300}=17.333・・・ \) より,\( 1800 \) 円が加算されます。
つまり,\( 6300 \; m \) 移動したときの金額Aは,\( 700+1800=2500 \)(円)になります。
Q , R
\( 6300 \; m \) 移動したときの金額Bは,\( 2900-2500=400 \)(円)なので,
あてはまるのは,「 \( 480 \) 秒をこえて \( 600 \) 秒まで」 になります。
大問3
ある高校の1年生が,ハンドボール投げの測定を行った。図1は,1組から3組のうちのある組について,\( 35 \) 人の測定結果をヒストグラムに表したものである。このヒストグラムでは,例えば,\( 4 \) ~ \( 8 \) の階級では,測定結果が \( 4 \; m \) 以上 \( 8 \; m \) 未満の人数が \( 2 \) 人であったことを表している。
このとき,次の各問いに答えなさい。ただし,測定結果はすべて自然数である。
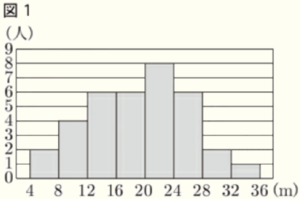
(1) 次は,図1のヒストグラムからいえることについて述べた文章である。 A , B に当てはまる数を入れて,文章を完成しなさい。ただし, B は小数第3位を四捨五入して答えなさい。
測定結果の最頻値は A \( m \) である。また,\( 16 \; m \) 未満の人数の累積相対度数は B である。
【解答】
A ・・・ \( 22 \)
B ・・・ \( 0.34 \)
【解説】
A
最頻値とは,度数がもっとも大きい階級の階級値のことです。
度数がもっとも大きい階級は,\( 20 \; m \) 以上 \( 24 \; m \) 未満の階級なので,
その階級値は,\( \dfrac{20+24}{2}=22 \; (m) \) になります。
B
累積相対度数は,【ある階級の累積度数 \( \div \) すべての階級の度数の合計】で求めることができます。
\( 16 \; m \) 未満の階級の累積度数は \( 2+4+6=12 \)(人)
すべての階級の度数の合計は,その組全員の人数なので,\( 35 \) 人
よって,累積相対度数は,
\( 12 \div 35=0.3428・・・ \)
小数第3位を四捨五入すると,\( 0.34 \)
(2) 図2は,1組,2組,3組の,それぞれ \( 35 \) 人の測定結果を箱ひげ図に表したものである。
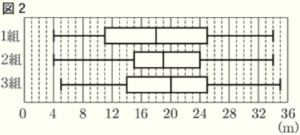
ここで,1組の箱ひげ図が図1のヒストグラムに対応していないことは,次のように説明できる。
図1のヒストグラムで,第1四分位数が入っている階級は \( 12 \; m \) 以上 \( 16 \; m \) 未満であるが,1組の箱ひげ図の第1四分位数はこの階級に入っていないからである。
2組と3組の箱ひげ図のうち,図1のヒストグラムに対応していないのはどちらであると考えられるか,下のア,イから1つ選び,記号で答えなさい。また,そのように考えた理由を,「図1のヒストグラムで,」につづけてかきなさい。
ア 2組 イ 3組
【解答】
イ
図1のヒストグラムで,
中央値が入っている階級は \( 16 \; m \) 以上 \( 20 \; m \) 未満であるが,
3組の箱ひげ図の中央値はこの階級に入っていないから。
【解説】
全部で \( 35 \) 人のデータを集計した結果なので,中央値は,値の小さい方から18番目の値になります。
図1のヒストグラムで,各階級の累積度数を確認すると,\( 16 \; m \) 以上 \( 20 \; m \) 未満の階級の累積度数が
\( 18 \) 人になっているので,中央値は \( 16 \; m \) 以上 \( 20 \; m \) 未満の階級に入っていることがわかります。
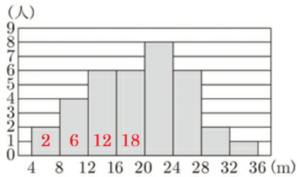
これに対して,3組の箱ひげ図では中央値は \( 20 \; m \) で,\( 20 \; m \) 以上 \( 24 \; m \) 未満の階級に入っているので,
図1のヒストグラムに対応していないといえます。
(3) 後日,図1のヒストグラムの \( 35 \) 人のデータのうちの1つが,\( 26 \; m \) ではなく \( 20 \; m \) であることがわかった。データの修正前と修正後で値が変わるものを,次のア~オからすべて選び,記号で答えなさい。
ア 第1四分位数 イ 中央値 ウ 第3四分位数 エ 四分位範囲 オ 平均値
【解説】
ここまでの内容から,図1のヒストグラムが対応している箱ひげ図は2組のものです。
2組の箱ひげ図に注目すると,第3四分位数(大きい方から9番目の値)が \( 24 \; m \) であることから,
修正前の \( 26 \; m \) のデータは大きい方から2~8番目のどこかにあったとわかります。
また,中央値(大きい方から18番目の値)が \( 19 \; m \) であることから,
修正後の \( 20 \; m \) のデータは大きい方から9~17番以内のどこかになることがわかります。
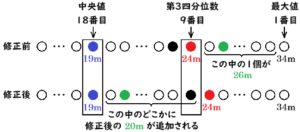
ここまでを参考にア~オのそれぞれの値が変わるか確認します。
【ア 第1四分位数】と【イ 中央値】
修正前の \( 26 \; m \) のデータと修正後の \( 20 \; m \) のデータは,
どちらも中央値 \( 19 \; m \) よりも大きい値なので,第一四分位数と中央値の値は変わりません。
【ウ 第3四分位数】
箱ひげ図から,大きい方から9番目の値は \( 24 \; m \) であり,
ヒストグラムから,修正前の \( 24 \; m \) 以上の記録の人は9人なので,
大きい方から10番目(上の図で●)のデータは \( 24 \; m \) 未満であったことがわかります。
ここから,修正後には \( 26 \; m \) のデータが1個なくなるので,
修正後の \( 24 \; m \) 以上の記録の人は8人になります。
つまり,修正前の大きい方から10番目のデータまたは修正後の \( 20 \; m \) のデータが
第3四分位数になるので,第3四分位数の値は変わります。
【エ 四分位範囲】
四分位範囲は「第3四分位数 \( – \) 第1四分位数」で求めることができます。
第3四分位数の値が変わり,第1四分位数の値は変わらないので,四分位範囲の値は変わります。
【オ 平均値】
平均値は,「すべてのデータの合計 \( \div \) データの個数」で求めることができます。
データの1つの値だけが変化するとき,すべてのデータの合計も変わります。
データの個数は変わらないので,平均値は変わります。
大問4
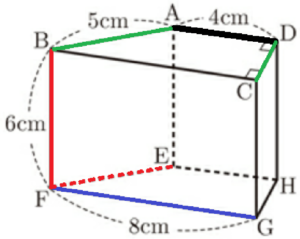
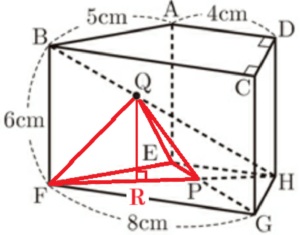
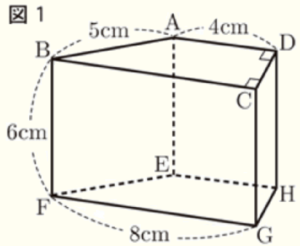
図1は,点 \( A,B,C,D,E,F,G,H \) を頂点とし,4つの側面がそれぞれ長方形である四角柱で,\( AB=5 \; cm,AD=4 \; cm,BF=6 \; cm, \)
\( FG=8 \; cm,∠ADC=∠BCD=90° \) である。
このとき,次の各問いに答えなさい。
(1) 辺 \( AD \) とねじれの位置にある辺を,次のア~オから2つ選び,記号で答えなさい。
ア 辺 \( AB \) イ 辺 \( BF \) ウ 辺 \( CD \) エ 辺 \( EF \) オ 辺 \( FG \)
【解説】
ねじれの位置にある辺とは,どこまで延ばしても交わらない2辺のうち,
平行なものを除いた辺の関係のことです。
【ア 辺 \( AB \),ウ 辺 \( CD \) 】
辺 \( AD \) と交わるのでねじれの辺ではありません。
【オ 辺 \( FG \) 】
辺 \( AD \) と平行なのでねじれの辺ではありません。
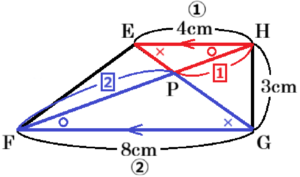
(2) 辺 \( GH \) の長さを求めなさい。
【解説】
この四角柱において,四角形 \( ABCD \) と四角形 \( EFGH \) は合同なので,
\( EF=AB=5 \; cm,EH=AD=4 \; cm \) です。
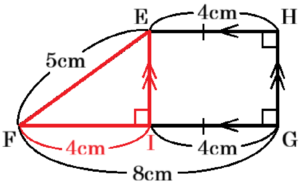
点 \( E \) から、辺 \( FG \) に垂線をひき,
交点を \( I \) とすると,
\( ∠ADC=∠BCD=90° \) より,
\( EH//FG \) なので,
\( IG=EH=4 \; cm \) であり,
\( FI=FG-IG=4 \; cm \) です。
\( △EFI \) は斜辺が \( 4 \; cm \),他の1辺が \( 4 \; cm \) の直角三角形,
つまり,3辺の比が \( 3:4:5 \) の直角三角形なので,\( EI=3 \; cm \) であり,
\( EI//GH \) より,\( GH=EI=3 \; cm \)
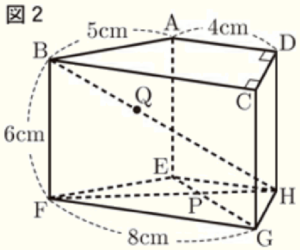
(3) 図2は,2つの線分 \( EG,FH \) の交点を \( P \) とし,線分 \( BH \) 上に点 \( Q \) を,線分 \( BQ \) と線分 \( QH \) の長さの比が \( BQ:QH=2:3 \) となるようにとったものである。
1 \( △EFP \) の面積を求めなさい。
【解答】
\( △EFP=4 \; cm^2 \)
【解説】
\( △PEH \) と \( △PGF \) において,
\( EH//FG \) より,錯角は等しいので,
\( ∠PEH=∠PGF,∠PHE=∠PFG \)
2組の角がそれぞれ等しいので,
\( △PEH \) ∽ \( △PGF \)
対応する辺の比は広しいので,
\( HP:FP=EH:FG=1:2 \)
\( △EFP \) と \( △EFH \) は高さが共通なので,
\( △EFP:△EFH=FP:FH=2:3 \)
\( △EFP=\dfrac{2}{3}△EFH \)
\( △EFH \) の面積は,
\( △EFH=4 \times 3 \times \dfrac{1}{2}=6 \; (cm^2) \)
なので,
\( △EFP=\dfrac{2}{3} \times 6=4 \; (cm^2) \)
2 三角すい \( QEFP \) の体積を求めなさい。
【解答】
三角すい \( QEFP=\dfrac{24}{5} \; cm^3 \)
【解説】
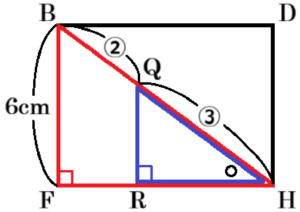
点 \( Q \) から面 \( EFP \) に垂線をひき,
交点を \( R \) とすると,
\( QR \) は, \( △EFP \) を底面としたときの
高さであり,
点 \( R \) は線分 \( FH \) 上の点になります。
面 \( BFHD \) に注目すると,
\( △BFH \) と \( △QRH \) において,
仮定より,
\( ∠BFH=∠QRH=90° \)
\( ∠BHF=∠QHR \)
2組の角がそれぞれ等しいので,
\( △BFH \) ∽ \( △QRH \)
対応する辺の比は等しいので,\( BQ:QH=2:3 \) より,
\( BF:QR=(BQ+QH):QH=5:3 \)
\( QR=\dfrac{3}{5}BF\)
\( =\dfrac{3}{5} \times 6 \)
\( =\dfrac{18}{5} \; (cm) \)
よって,三角すい \( QEFP \) の体積は,
\( 4 \times \dfrac{18}{5} \times \dfrac{1}{3}=\dfrac{24}{5} \; (cm^3) \)
大問5
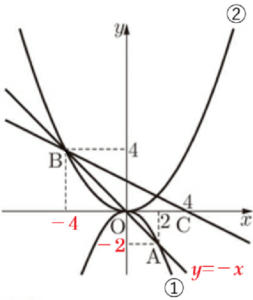
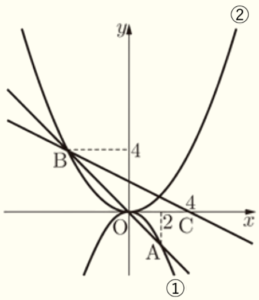
右の図のように,2つの関数
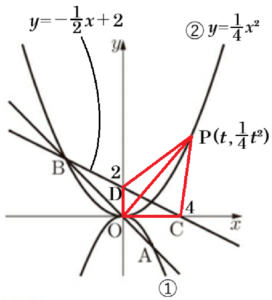
\( y=-\dfrac{1}{2}x^2 \) ・・・ ➀
\( y=ax^2 \)(\( a \) は定数) ・・・ ➁
のグラフがある。
点 \( A \) は関数➀のグラフ上にあり,\( x \) 座標は \( 2 \) である。点 \( B \) は関数➁のグラフ上にあり,\( y \) 座標が \( 4 \) で,直線 \( AB \) は原点 \( O \) を通る。また,点 \( C \) の座標は \( (4,0) \) である。
このとき,次の各問いに答えなさい。
(1) \( a \) の値を求めなさい。
【解答】
\( a=\dfrac{1}{4} \)
【解説】
点 \( A \) は \( y=-\dfrac{1}{2}x^2 \) 上の点で,\( x \) 座標が \( 2 \) なので,
\( y \) 座標の値は
\( y=-\dfrac{1}{2} \times 2^2=-2 \)
直線 \( AB \) は原点と \( A(2,-2) \) を通るので,
直線 \( AB \) の式は,\( y=-x \)
点 \( B \) は \( y=-x \) 上の点で,\( y \) 座標が \( 4 \) なので,
\( x \) 座標の値は \( -4 \)
\( y=ax^2 \) のグラフは,\( B(-4,4) \) を通るので,
\( 4=a \times (-4)^2 \)
\( 4=16a \)
\( a=\dfrac{1}{4} \)
(2) 直線 \( BC \) の式を求めなさい。
【解答】
\( y=-\dfrac{1}{2}x+2 \)
【解説】
直線 \( BC \) の式を \( y=mx+n \) とすると,
\( B(-4,4) \) と \( C(4,0) \) を通るので,
\( m=\dfrac{0-4}{4-(-4)}=-\dfrac{1}{2} \)
\( y=-\dfrac{1}{2}x+n \) に \( x=4,y=0 \) を代入すると,
\( 0=-\dfrac{1}{2} \times 4+n \)
\( n=2 \)
よって,直線 \( BC \) の式は \( y=-\dfrac{1}{2}x+2 \)
(3) 直線 \( BC \) と \( y \) 軸との交点を \( D \) とする。また,関数➁のグラフ上において,\( x \) 座標が \( 2 \) より大きい点 \( P \) をとる。
\( P \) の \( x \) 座標を \( t \) とするとき,
1 四角形 \( OCPD \) の面積を,\( t \) を使った式で表しなさい。
【解答】
\( \dfrac{1}{2}t^2+t \)
【解説】
点 \( P \) は \( y=\dfrac{1}{4}x^2 \) 上の点で,\( x \) 座標が \( t \) なので,
\( y \) 座標の値は \( \dfrac{1}{4}t^2 \) と表すことができます。
四角形 \( OCPD \) を \( △OPD \) と \( △OPC \) に分けて考えると,
\( △OPD,△OPC \) の面積は,
\( △OPD=2 \times t \times \dfrac{1}{2}=t \)
\( △OPC=4 \times \dfrac{1}{4}t^2 \times \dfrac{1}{2}=\dfrac{1}{2}t^2 \)
と表すことができるので,
四角形 \( OCPD=△OPD+△OPC \)
\( =\dfrac{1}{2}t^2+t \)
と表すことができます。
2 四角形 \( OCPD \) の面積が,\( △BAC \) の面積の2倍となるような \( t \) の値を求めなさい。
【解説】
1 で四角形 \( OCPD \) の面積が \( \dfrac{1}{2}t^2+t \) で表せることがわかっているので,
\( △BAC \) の面積を \( S \) とすると,四角形 \( OCPD \) の面積と \( △BAC \) の面積の関係は,
\( \dfrac{1}{2}t^2+t=2S \) となります。
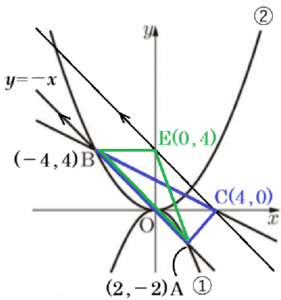
辺 \( BA \) を \( △BAC \) の底辺として,
点 \( C \) を通り,直線 \( AB \) と平行な直線と \( y \) 軸との交点を \( E \) とすると,
等積変形の考え方から,\( △BAC \) と \( △BAE \) の
面積は等しくなります。
\( △BAE \) を \( △BOE \) と \( △AOE \) に分けると,
\( △BOE,△AOE \) の面積は,
\( △BOE=4 \times 4 \times \dfrac{1}{2}=8 \)
\( △AOE=4 \times 2 \times \dfrac{1}{2}=4 \)
なので,
\( △BAE=△OPD+△OPC \)
\( =8+4 \)
\( =12 \)
です。
よって,四角形 \( OCPD \) の面積が,\( △BAC \) の面積の2倍となるとき,
\( \dfrac{1}{2}t^2+t=2 \times 12 \)
\( t^2+2t=48 \)
\( t^2+2t-48=0 \)
\( (t-6)(t+8)=0 \)
\( t=6 \)( \( t>2 \) より)
大問6
次は,大輔さんと美咲さんが,数学の授業で先生と会話をしている場面である。会話文を読んで,あとの各問いに答えなさい。ただし,根号がつくときは,根号のついたままで答えること。
先生:今日は,コンピュータを使って図形の勉強をします。
では,次の課題について考えてみましょう。
(課題)
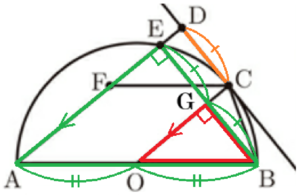
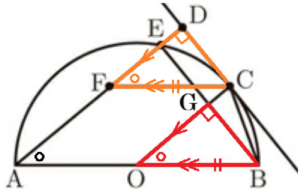
図1は,線分 \( AB \) を直径とする半円であり,点 \( O \) は \( AB \) の中点である。\( \stackrel{\huge\frown}{ AB } \) 上に点 \( C \) を,\( \stackrel{\huge\frown}{ AC } \) の長さが \( \stackrel{\huge\frown}{ BC } \) の長さより長くなるようにとる。点 \( D \) は \( C \) で半円と接する直線上にあり,\( AD//OC \) である。また,\( \stackrel{\huge\frown}{ AC } \) と線分 \( AD \) の交点を \( E \) とし,\( AD \) 上に点 \( F \) を,\( AF=AO \) となるようにとる。
このとき,\( △DFC \) と \( △EAB \) はどんな関係にあるか調べなさい。
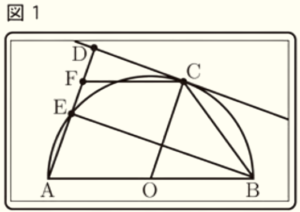
先生:点 \( C \) を \( \stackrel{\huge\frown}{ AB } \) 上のどこにとるかによって,3点 \( D,E,F \) の位置が変わり,\( △DFC \) と \( △EAB \)
の形や大きさも変わります。\( C \) を \( \stackrel{\huge\frown}{ AB } \) 上で,\( \stackrel{\huge\frown}{ AC } \) の長さが \( \stackrel{\huge\frown}{ BC } \) の長さより長くなる条件で
動かせるようにしたので,動かしてみてください。
大輔:先生,\( C \) の位置を変えてみたら,\( F \) が線分 \( DE \) 上ではなく,図2のように,線分 \( AE \) 上に
とれました。
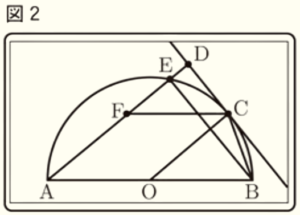 先生:そうですね。それでは,課題にある,\( △DFC \) と \( △EAB \) はどんな関係にありますか。
先生:そうですね。それでは,課題にある,\( △DFC \) と \( △EAB \) はどんな関係にありますか。
美咲:\( C \) の位置に関係なく,\( △DFC \) と \( △EAB \) は相似になりそうです。
先生:その通りです。では,相似になることを証明してみましょう。
(1) 下線部について,\( △DFC \) ∽ \( △EAB \) であることを証明しなさい。
【解答】
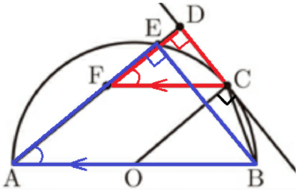
\( △DFC \) と \( △EAB \) において,
直径 \( AB \) に対する円周角なので,
\( ∠AEB=90° \) ・・・ ➀
仮定より,直線 \( CD \) は,点 \( C \) における円 \( O \) の接線なので,
\( OC⊥CD \)
仮定より,\( AD//OC \) なので,\( AD⊥CD \) でもあり,
\( ∠FDC=90° \) ・・・ ➁
➀➁より,
\( ∠FDC=∠AEB \) ・・・ ➂
仮定より,\( AF=AO \) ・・・ ➃
円 \( O \) の半径なので,
\( CO=AO \) ・・・ ➄
➃➄より,
\( AF=CO \) ・・・ ⑥
さらに,\( AD//OC \) でもあることから,
四角形 \( AOCF \) はひし形(注)であり,
\( FC//AB \)
ここから,同位角は等しいので,
\( ∠DFC=∠EAB \) ・・・ ⑦
➂➆より,
2組の角がそれぞれ等しいので,
\( △DFC \) ∽ \( △EAB \)
\( \phantom{ } \)
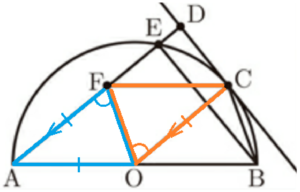
注:四角形AOCFがひし形とわかる理由
\( △AOF \) と \( △CFO \) において,
仮定より,
\( AF=CO \) ・・・ ➀
\( AD//OC \) より錯角は等しいので,
\( ∠AFO=∠COF \) ・・・ ➁
辺 \( OF \) は共通 ・・・ ➂
➀➁➂より,
2組の辺とその間の角がそれぞれ等しいので,
\( △AOF≡△CFO \)
対応する辺は等しいので,\( AO=CF \)
よって,四角形 \( AOCF \) は4つの辺が
すべて等しいのでひし形といえます。
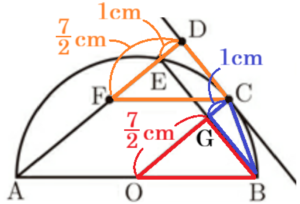
(2) 図2において,\( AB=9 \; cm,BC=3 \; cm \) のとき,
1 線分 \( DC \) の長さを求めなさい。
【解答】
\( DC=2\sqrt{2} \; cm \)
【解説】
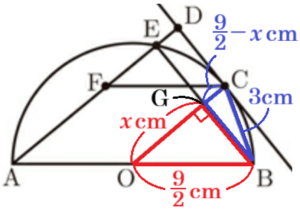
線分 \( BE \) と線分 \( OC \) の交点を \( G \) とすると,
\( ∠AEB=∠ADC=90°,AD//OC \) より \( DC=EG \) ・・・ ➀ になっています。
また,\( △EAB \) ∽ \( △GOB \) であり,
点 \( O \) は \( AB \) の中点であること,
\( AD//OC \) であることから,
点 \( G \) は \( EB \) の中点,つまり,\( EG=GB \) ・・・ ➁ になっています。
➀➁から,\( DC=GB \) になっています。
\( △BOG \) と \( △BCG \) において,
\( OG=x \; cm \) とすると,\( OC=OB=\dfrac{1}{2}AB=\dfrac{9}{2} \; cm \) なので,
\( CG=\left(\dfrac{9}{2}-x\right) \; cm \) と表すことができ,
三平方の定理より,
\( BO^2-OG^2=BC^2-CG^2 \)
\( \left(\dfrac{9}{2}\right)^2-x^2=3^2-\left(\dfrac{9}{2}-x\right)^2 \)
\( x=\dfrac{7}{2} \; (cm) \)
\( △BOG \) において,三平方の定理より,
\( BG^2=BO^2-OG^2 \)
\( =\left(\dfrac{9}{2}\right)^2-\left(\dfrac{7}{2}\right)^2 \)
\( =8 \)
\( BG=2\sqrt{2} \; (cm) \)(\( BG>0 \) より)
よって,\( DC=BG=2\sqrt{2} \; cm \)
2 線分 \( EF \) の長さを求めなさい。
【解答】
\( EF=\dfrac{5}{2} \; cm \)
【解説】
\( △BOG \) と \( △CFD \) において,
ここまでの結果から,
\( ∠OGB=∠FDC=90° \)
\( OB=AO=FC \)
\( AD//OC,FC//AB \) なので,
\( ∠GOB=∠DAB=∠DFC \)
直角三角形において,
斜辺と他の1つの鋭角がそれぞれ等しいので,
\( △BOG≡△CFD \)
合同な三角形の対応する辺は等しいので,
1より,
\( FD=OG=\dfrac{7}{2} \; cm \)
\( OC=OB=\dfrac{1}{2}AB=\dfrac{9}{2} \; cm \) より,
\( GC=OC-OG=1 \; (cm) \)
\( AD//OC,DC//EB \) より,\( ED=GG=1 \; cm \) なので,
\( EF=FD-ED=\dfrac{5}{2} \; (cm) \)





 先生:そうですね。それでは,課題にある,\( △DFC \) と \( △EAB \) はどんな関係にありますか。
先生:そうですね。それでは,課題にある,\( △DFC \) と \( △EAB \) はどんな関係にありますか。