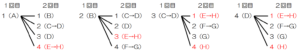大問1
1 \( 5-(-4) \) を計算しなさい。
2 \( 6 \div \left( -\dfrac{2}{7} \right) \) を計算しなさい。
【解説】
\( =6 \times \left( -\dfrac{7}{2} \right) \)
\( =-\dfrac{6 \times 7}{2} \)
\( =-21 \)
3 \( (-2a)^2 \times 5b \) を計算しなさい。
【解説】
\( =4a^2 \times 5b \)
\( =20a^2b \)
4 等式 \( a+7b-3=0 \) を \( b \) について解きなさい。
【解答】
\( b=-\dfrac{1}{7}a+\dfrac{3}{7} \)
【解説】
\( b \) について解くということは,\( b=\boxed{ } \) の形で表すということなので,
\( a+7b-3=0 \)
\( 7b=-a+3 \)
\( b=-\dfrac{1}{7}a+\dfrac{3}{7} \)
5 \( \dfrac{15}{\sqrt{3}}+\sqrt{27} \) を計算しなさい。
【解説】
\( =\dfrac{15 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}+3\sqrt{3} \)
\( =5\sqrt{3}+3\sqrt{3} \)
\( =8\sqrt{3} \)
6 \( y \) は \( x \) の2乗に比例し,\( x=6 \) のとき \( y=-9 \) です。このとき,\( y \) を \( x \) の式で表しなさい。
【解答】
\( y=-\dfrac{1}{4}x^2 \)
【解説】
\( y \) が \( x \) の2乗に比例することを表す式は \( y=ax^2 \) になります。
\( y=ax^2 \) に \( x=6,y=-9 \) を代入すると,
\( -9=a \times 6^2 \)
\( 36a=-9 \)
\( a=-\dfrac{1}{4} \)
なので,求める式は \( y=-\dfrac{1}{4}x^2 \) になります。
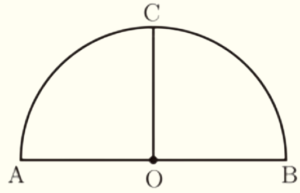
7 右の図のような,線分 \( AB \) を直径とする半円があり,線分 \( AB \) の中点を \( O \) とします。点 \( O \) を通って線分 \( AB \) に垂直な直線と \( AB \) との交点を \( C \) とします。\( \stackrel{\huge\frown}{ BC } \) 上にあって,\( ∠POB=45° \) となる点 \( P \) を作図によって求めるとき,その作図の方法を説明したものとして,誤っているものを,あとのア~エから1つ選び,記号で答えなさい。
ア \( ∠COB \) の二等分線と \( \stackrel{\huge\frown}{ BC } \) との交点を \( P \) とする。
イ 点 \( A \) と点 \( C \) を結び,\( ∠CAB \) の二等分線と \( \stackrel{\huge\frown}{ BC } \) との交点を \( P \) とする。
ウ 点 \( B \) と点 \( C \) を結び,線分 \( BC \) の垂直二等分線と \( \stackrel{\huge\frown}{ BC } \) との交点を \( P \) とする。
エ 線分 \( OC \) の垂直二等分線と \( \stackrel{\huge\frown}{ BC } \) との交点を \( P \) とする。
【解説】
ア
仮定より \( ∠COB=90° \) なので,
\( ∠COB \) の二等分線と線分 \( OB \) がなす角は \( 45° \) になります。
よって,点 \( P \) が \( ∠COB \) の二等分線上の点であることから,\( ∠POB=45° \) になります。
\( \phantom{ } \)
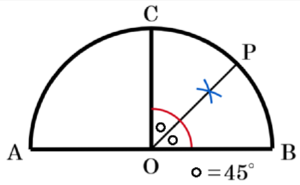
イ
\( △OAC \) は直角二等辺三角形なので \( ∠CAB=45° \) であり,
線分 \( PA \) は \( ∠CAB \) の二等分線であることから,
\( ∠PAB=\dfrac{1}{2}∠CAB=22.5° \)
になります。
\( ∠PAB \) は \( \stackrel{\huge\frown}{ PB } \) に対する円周角,\( ∠POB \) は \( \stackrel{\huge\frown}{ PB } \) に対する中心角なので,
\( ∠POB=2∠PAB=45° \)
になります。
\( \phantom{ } \)
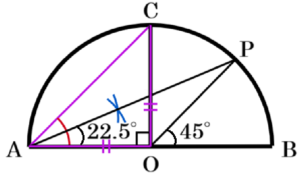
ウ
\( △OBC \) は直角二等辺三角形なので,線分 \( BC \) の垂直二等分線は \( ∠COB \) の二等分線になります。
\( ∠COB=90° \) であることから,
\( ∠POB=45° \) になります。
\( \phantom{ } \)
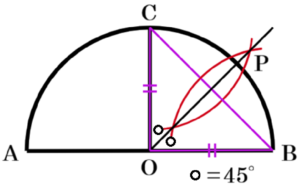
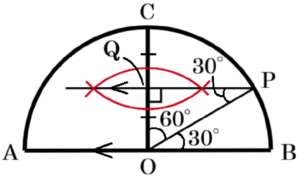
エ
線分 \( OC \) の垂直二等分線と線分 \( OC \) の交点を
\( Q \) とすると,点 \( Q \) は線分 \( OC \) の中点なので,
\( OQ:OP=1:2 \) であり,\( △OPQ \) は \( 30°,60°,90° \) の直角三角形になっています。
このとき,\( ∠OPQ=30° \) であり,
\( PQ//OB \) であることから,錯角は等しいので,
\( ∠POB=∠OPQ=30° \) であり,
\( 45° \) にはなりません。
\( \phantom{ } \)
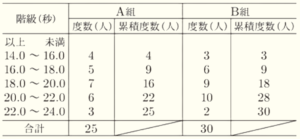
8 ある学年で,クロールで \( 25 \; m \) を泳いだときの記録をとりました。下の表は,このときの,A組の生徒 \( 25 \) 人とB組の生徒 \( 30 \) 人の記録を,累積度数をふくめて度数分布表に整理したものです。
A組とB組を比べたとき,\( 18.0 \) 秒以上 \( 20.0 \) 秒未満の階級の累積相対度数が大きい組と,その累積相対度数を答えなさい。
【解答】
大きい方の組 ・・・ A組
累積相対度数 ・・・ \( 0.64 \)
【解説】
ある階級の累積相対度数は,
その階級の累積度数 \( \div \) すべての階級の度数の合計
で求めることができます。
【A組の累積相対度数】
\( 18.0 \) 秒以上 \( 20.0 \) 秒未満の階級の累積度数は \( 16 \) 人
すべての階級の度数の合計(クラスの人数)は \( 25 \) 人
\( 18.0 \) 秒以上 \( 20.0 \) 秒未満の階級の累積相対度数は
\( 16 \div 25=0.64 \)
【B組の累積相対度数】
\( 18.0 \) 秒以上 \( 20.0 \) 秒未満の階級の累積度数は \( 18 \) 人
すべての階級の度数の合計(クラスの人数)は \( 30 \) 人
\( 18.0 \) 秒以上 \( 20.0 \) 秒未満の階級の累積相対度数は
\( 18 \div 30=0.60 \)
大問2
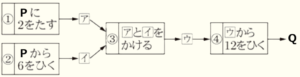
1 下の図は,P に整数を入れると,➀~➃の順に計算が行われ,Q の値が導き出される過程を表しています。 \( \boxed{ア} \) には➀,\( \boxed{イ} \) には➁,\( \boxed{ウ} \) には➂の計算を行った結果の値がそれぞれ入ります。
あとの(1),(2)の問いに答えなさい。
(1) P に入れる整数を \( 1 \) とするとき,Q の値を求めなさい。
【解説】
P に \( 1 \) を入れると,
\( \boxed{ア}=1+2=3 \)
\( \boxed{イ}=1-6=-5 \)
であり,
\( \boxed{ウ}=\boxed{ア} \times \boxed{イ} \)
\( =3 \times -5 \)
\( =-15 \)
なので,
Q \( =\boxed{ウ}-12 \)
\( =-15-12 \)
\( =-27 \)
(2) P にある整数を入れると,Q の値が P に入れた整数と同じ値になりました。P に入れた整数を \( x \) とするとき,\( x \) をすべて求めなさい。
【解説】
P 入れた整数を \( x \) とすると,
\( \boxed{ア}=x+2 \)
\( \boxed{イ}=x-6 \)
と表すことができるので,
\( \boxed{ウ}=\boxed{ア} \times \boxed{イ} \)
\( =(x+2)(x-6) \)
ここから,
Q の値は,
Q \( =\boxed{ウ}-12 \)
\( =(x+2)(x-6)-12 \)
と表すことができます。
Q の値が P に入れた整数 \( x \) と同じ値になるとき,
\( (x+2)(x-6)-12=x \)
\( (x^2-4x-12)-12=x \)
\( x^2-5x-24=0 \)
\( (x+3)(x-8)=0 \)
\( x=-3,8 \)
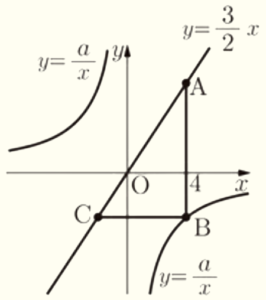
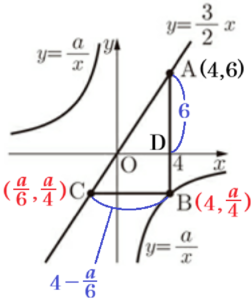
2 右の図のように,比例 \( y=\dfrac{3}{2}x \) のグラフ上と反比例 \( y=\dfrac{a}{x} \) のグラフ上に,\( x \) 座標が \( 4 \) である点 \( A \),点 \( B \) をそれぞれとり,点 \( A \) と点 \( B \) を結びます。また,比例 \( y=\dfrac{3}{2}x \) のグラフ上に,点 \( B \) と \( y \) 座標が等しい点 \( C \) をとり,点 \( B \) と点 \( C \) を結びます。ただし,\( a<0 \) とします。
次の(1),(2)の問いに答えなさい。
(1) 点 \( A \) の \( y \) 座標を求めなさい。
【解説】
点 \( A \) は,\( y=\dfrac{3}{2}x \) 上の点で,
\( x \) 座標が \( 4 \) なので,
\( y \) 座標の値は,
\( y=\dfrac{3}{2} \times 4=6 \)
(2) 線分 \( AB \) と\( x \) 軸との交点を \( D \) とします。\( AD=BC \) となるとき,\( a \) の値を求めなさい。
【解説】
点 \( B \) は,\( y=\dfrac{a}{x} \) 上の点で,\( x \) 座標が \( 4 \) なので,
\( y \) 座標の値は,
\( y=\dfrac{a}{4} \)
点 \( C \) は,\( y=\dfrac{3}{2}x \) 上の点で,\( y \) 座標が \( \dfrac{a}{4} \) なので,
\( x \) 座標の値は,
\( \dfrac{a}{4}=\dfrac{3}{2}x \)
\( x=\dfrac{a}{6} \)
ここから,\( BC \) の長さは,
\( BC=4-\dfrac{a}{6} \)
と表すことができます。
\( A(4,6),D(4,0) \) より,\( AC=6 \) なので,
\( AD=BC \) のとき,
\( 6=4-\dfrac{a}{6} \)
\( \dfrac{a}{6}=-2 \)
\( a=-12 \)
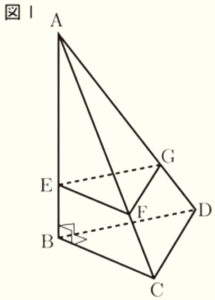
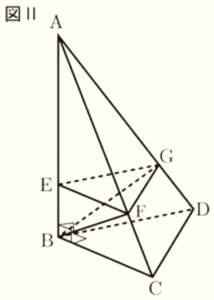
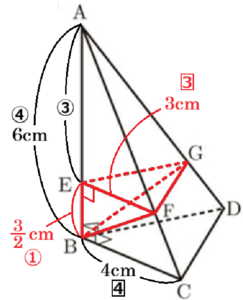
3 図Ⅰのような,\( ∠ABC=∠ABD=∠DBC=90° \) である三角錐 \( ABCD \) があります。辺 \( AB \) 上に,点 \( E \) を \( AE:EB=3:1 \) となるようにとります。また,辺 \( AC \),辺 \( AD \) 上に,それぞれ点 \( F \),点 \( G \) を面 \( BCD \) と面 \( EFG \) が平行となるようにとります。
次の(1),(2)の問いに答えなさい。
(1) 三角錐 \( ABCD \) と三角錐 \( AEFG \) の体積の比を求めなさい。
【解説】
三角すいを4つの面のうち1つの面に平行な面で切ってできる小さい三角すいは,
もとの三角すいと相似になります。
また,相似な立体の対応する辺の比はすべて等しいので,体積比は相似比の3乗の比と等しくなります。
\( AE:EB=3:1 \) より、相似比は \( AB:AE=4:3 \) なので,
体積比は,
\( 4^3:3^3=64:27 \)
(2) 図Ⅱは,図Ⅰにおいて,点 \( B \) と点 \( F \),点 \( B \) と点 \( G \) をそれぞれ結んだものです。
\( AB=6 \; cm,BC=BD=4 \; cm \) のとき,三角錐 \( BEFG \) の体積を求めなさい。
【解答】
\( \dfrac{9}{4} \; cm^3 \)
【解説】
三角すい \( ABCD \) と三角すい \( AEFG \) の相似比は \( 4:3 \) なので,
\( EF=EG=4 \times \dfrac{3}{4}=3 \; (cm) \)
\( AE:EB=3:1 \) より,
\( EB=6 \times \dfrac{1}{4}=\dfrac{3}{2} \; (cm) \)
よって,三角すい \( BEFG \) の体積は,
\( \left( 3 \times 3 \times \dfrac{1}{2} \right) \times \dfrac{3}{2} \times \dfrac{1}{3}=\dfrac{9}{4} \; (cm^3) \)
4 次の図のような,円盤,マス目,コマがあります。円盤には,\( 1 \) から \( 4 \) までの数字が書いてあります。この円盤はまわすことができ,円盤とは別に針が固定されています。まわした円盤が静止すると,針が指す場所に書いてある数字が,必ず1つ決まります。マス目には,スタートの文字と,\( A \) から \( H \) までのアルファベットが書いてあり,\( C,E,F \) のマスには指示が書いてあります。
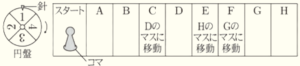
円盤を1回まわすごとに,次の ルール にしたがってコマを移動させます。
ルール
・円盤をまわして決まった数字と同じ数のマスだけ,コマがあるマスから \( H \) のマスの方向に
向かって,コマを移動させる。
・コマを移動させて \( C,E,F \) のマスに止まったときは,それぞれそのマスに書いてある指示に
したがってコマを移動させる。
たとえば,コマをスタートのマスに置き,円盤を1回まわして決まった数字が \( 2 \) のとき,\( B \) のマスにコマを移動させます。
次の(1),(2)の問いに答えなさい。ただし,円盤をまわして決まる数字は,\( 1 \) から \( 4 \) までのどの数字に決まることも同様に確からしいものとします。
(1) コマをスタートのマスに置き,円盤を1回まわします。このとき,コマが \( D \) のマスにある確率を求めなさい。
【解説】
円盤をまわして決まった数字とそれ折れにおけるコマの移動先は次のとおり,
数字が \( 1 \) のとき → \( A \) のマスに移動
数字が \( 2 \) のとき → \( B \) のマスに移動
数字が \( 3 \) のとき → \( C \) のマスに移動し,\( C \) のマスの指示により \( D \) のマスに移動
数字が \( 4 \) のとき → \( D \) のマスに移動
よって,すべての場合の数は4通り,コマが \( D \) のマスにあるのは2通りなので,
求める確率は \( \dfrac{2}{4}=\dfrac{1}{2} \)
(2) コマをスタートのマスに置き,円盤を2回まわします。このとき,コマが \( H \) のマスにある確率を求めなさい。
【解説】
「1回目に決まった数字とコマの移動先」と「2回目に決まった数字とコマの移動先」の
組み合わせを樹形図に書き出すと下の図のようになります。
コマが \( H \) のマスにある組み合わせは6通り,
すべての組み合わせは16通りなので,
求める確率は \( \dfrac{6}{16}=\dfrac{3}{8} \)
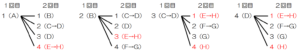
大問3
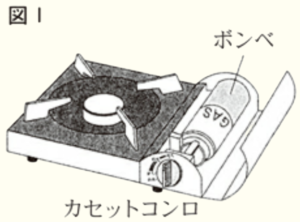
花さんと大地さんは,図Ⅰのような,ボンべをセットして使用するカセットコンロの,ガスの消費量やボンべに残るガスの量について調べています。
次の1,2の問いに答えなさい。
1 花さんは,カセットコンロのガスの消費量をウェブサイトで調べました。下の表は,カセットコンロの用途と,それぞれの用途で1回使用したときのガスの消費量についてまとめたものです。
この表をもとにしてガスの消費量を考えるとき,あとの(1),(2)の問いに答えなさい。

(1) 表の ➀ の用途で \( a \) 回,➁ の用途で \( b \) 回使用するとき,ガスの消費量の合計を \( a \) と \( b \) を使った式で表しなさい。
【解説】
➀ の用途で1回使用するときのガスの消費量は \( 50 \; g \) なので,
\( a \) 回使用するときのガスの消費量は \( 50a \; g \)
➁ の用途で1回使用するときのガスの消費量は \( 15 \; g \) なので,
\( b \) 回使用するときのガスの消費量は \( 15b \; g \)
と表すことができます。
ガスの消費量の合計は,これらの和なので,\( 50a+15b \; g \) となります。
(2) 花さんの自宅には,ガスが \( 240 \; g \) 入ったボンベが \( 6 \) 本あります。➁ の用途で使用する回数が ➀ の用途で使用する回数の2倍となるようにして,このボンベ \( 6 \) 本分のガスをすべて消費するとき,➀ の用途で使用できる回数は何回になりますか。
【解説】
(1)と同様に
➀ の用途で \( a \) 回,
➁ の用途で \( b \) 回使用すると考えると,
➁ の用途で使用する回数が
➀ の用途で使用する回数の2倍となるとき,
\( b=2a \) と表すことができます。
これを(1)の \( 50a+15b \) に代入すると,\( 50a+15 \times 2a=80a \) と表すことできます。
ガスが \( 240 \; g \) 入ったボンベ \( 6 \) 本分のガスの総量は
\( 240 \times 6=1440 \; (g) \)
なので,
\( 80a=1440 \)
\( a=18 \)(回)
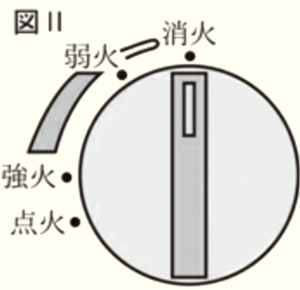
2 花さんと大地さんは,図Ⅰと同じカセットコンロA,Bを準備しました。これらのカセットコンロは,図Ⅱのようなつまみをまわして火の強さを調節できます。ボンべのガスの量が \( 240 \; g \) のとき,「強火」の設定では \( 60 \) 分間,「弱火」の設定では \( 180 \) 分間使用すると,それぞれボンべのガスがすべてなくなります。
次の(1),(2)の問いに答えなさい。ただし,火の強さを固定して使用するとき,火の強さに応じてガスは一定の割合で消費されるものとします。また,つまみをまわしているときの時間とガスの消費量は考えないものとします。
(1) ガスが \( 240 \; g \) 入ったボンべをセットして,カセットコンロを「強火」の設定で \( 20 \) 分間使用したあとに,ボンべに残るガスの量は何 \( g \) ですか。
【解説】
「強火」の設定のとき,\( 240 \; g \) のガスが \( 60 \) 分間でなくなるのだから,
\( 1 \) 分あたりに消費されるガスの量は,\( 240 \div 60=4 \; (g) \) です。
つまり,「強火」の設定で \( 20 \) 分間使用したときに消費されるガスの量は,
\( 4 \times 20=80 \; (g) \) なので,ボンべに残るガスの量は
\( 240-80=160 \; (g) \)
(2) 花さんと大地さんは,カセットコンロを使用したときにボンべに残るガスの量を調べようと思いました。はじめに,2人はカセットコンロA,Bにガスが \( 240 \; g \) 入ったボンべをそれぞれセットして同時に点火しました。次の \( \color{blue}{\boxed{ }} \) は,2人が点火したあと火の強さをそれぞれ設定し,カセットコンロを使用したようすを示したものです。
・ 花さんは,カセットコンロAを,「弱火」と「強火」の間に設定した。途中で火の強さを変えずに
使用し,点火してからちょうど \( 80 \) 分後にボンべのガスがすべてなくなった。
・ 大地さんは,カセットコンロBを,はじめに「強火」の設定で \( 40 \) 分間,そのあと,「弱火」の
設定に変えて使用した。使用し続けるとボンべのガスがすべてなくなった。
花さんと大地さんは,カセットコンロを使用したようすについて話し合いました。花さんと大地さんの会話の内容は次のとおりです。
あとの(ア),(イ)の問いに答えなさい。
会話
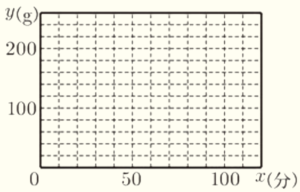
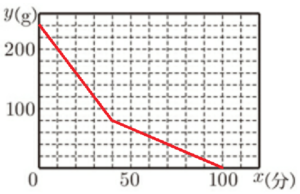
花さん :カセットコンロAについて,点火してからボンべのガスがすべてなくなるまでのグラフを
かいてみるね。カセットコンロを点火してから \( x \) 分後の,ボンべに残るガスの量を \( y \; g \)
とすると,\( x \) と \( y \) との関係を表すグラフは図Ⅲのようになるね。
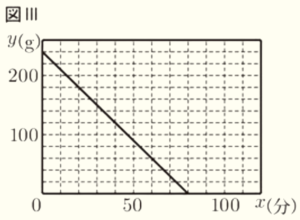
大地さん:私もカセットコンロBについて,花さんと同じようにグラフをかいてみよう。私のかいた
グラフを図Ⅲにかき写してみると何かわかることはあるかな。
花さん :点火してから \( 80 \) 分後までの間に,点火したときとは別に,それぞれのボンベに残るガスの
量が等しくなるときがあるね。
大地さん:ボンべに残るガスの量が等しくなるときのガスの量を表しているのは,2つのグラフの
a の値だね。計算して求めてみよう。
(ア) カセットコンロBについて,点火してからボンべのガスがすべてなくなるまでの,\( x \) と \( y \) との関係を表すグラフを,右の図に書き入れなさい。
【解説】
ボンベが満タン(\( x=0 \))のときから「強火」の設定で \( 40 \) 分間使用し,
そこ(\( x=40 \))から「弱火」の設定に変えてガスがなくなるまで使用したので,
\( 0≦x≦40 \) の範囲を表す直線と\( 0≦x≦\boxed{ ? } \) の範囲を表す直線と
2つをくっつけたものになります。
【\( 0≦x≦40 \) の範囲を表す直線】
「強火」の設定のとき,\( 1 \) 分あたりに消費されるガスの量は,\( 4 \; g \) で,
\( 40 \) 分間使用したときに消費されるガスの量は,
\( 4 \times 40=160 \; (g) \) なので,ボンべに残るガスの量は
\( 240-160=80 \; (g) \)
ここから,\( x=40 \) のときの \( y \) の値は \( y=80 \) になります。
また,ボンベが満タン(\( x=0 \))のときのガスの量は \( y=240 \; (g) \) なので,
\( 0≦x≦40 \) の範囲を表す直線は,\( (0,240) \) と \( (40,80) \) を結んだ直線になります。
【\( 40≦x≦\boxed{ ? } \) の範囲を表す直線】
「弱火」の設定のとき,\( 240 \; g \) のガスが \( 180 \) 分間でなくなるのだから,
\( 1 \) 分あたりに消費されるガスの量は,\( 240 \div 180=\dfrac{4}{3} \; (g) \) です。
ここから,ボンべに残った \( 240 \; g \) のガスがなくなるまでの時間は,
\( 80 \div \dfrac{4}{3}=60 \)(分)であり,
「強火」の設定で使用した \( 40 \) 分間と合わせて,\( x=40+60=100 \) のときに
ガスがすべてなくなることになります。
つまり,\( 40≦x≦\boxed{ ? } \) の範囲を表す直線は,\( (40,80) \) と \( (100,0) \) を結んだ直線になります。
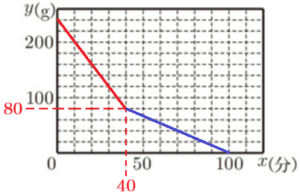
(イ) 会話の a にあてはまる適切な言葉を書きなさい。また,点火したときとは別に,カセットコンロA,Bのそれぞれのボンべに残るガスの量が等しくなるときの,ボンべに残るガスの量を求めなさい。
【解答】
a ・・・ 交点の \( y \) 座標
ボンべに残るガスの量 ・・・ \( 48 \; g \)
【解説】
図Ⅲに(ア)のグラフを書き足すと,\( 40≦x≦100 \) の直線と交わります。
\( 40≦x≦100 \) の直線の式を \( y=-\dfrac{4}{3}x+b \) とすると,
\( (100,0) \) を通るので,
\( 0=-\dfrac{4}{3} \times 100+b \)
\( b=\dfrac{400}{3} \)
であり,この直線の式は \( y=-\dfrac{4}{3}x+\dfrac{400}{3} \) ・・・➀ になります。
また,図Ⅲの直線は,\( (0,240) \) と \( (80,0) \) を通るので,
傾きは \( \dfrac{0-240}{80-0}=-3 \) であり,
この直線の式は \( y=-3x+240 \) ・・・➁ になります。
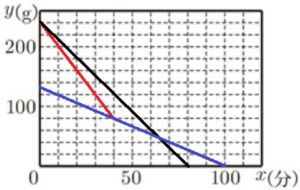
2つの直線の交点は,それぞれの直線の式を
連立方程式にしたときの解として表れます。
\( \left\{ \begin{array}{}
y=-\dfrac{4}{3}x+\dfrac{400}{3} \;\; ・・・ \;\; ➀ \\
y=-3x+240 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
を解くと \( x=64,y=48 \) なので,
求めるガスの量は \( 48 \; g \) になります。
連立方程式を解く
\( \left\{ \begin{array}{}
y=-\dfrac{4}{3}x+\dfrac{400}{3} \;\; ・・・ \;\; ➀ \\
y=-3x+240 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
\( -\dfrac{4}{3}x+\dfrac{400}{3}=-3x+240 \)
\( -4x+400=-9x+720 \)
\( 5x=320 \)
\( x=64 \)
➁に代入すると,
\( y=-3 \times 64+240=48 \)
大問4
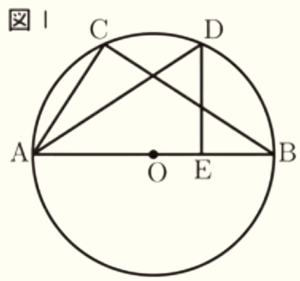
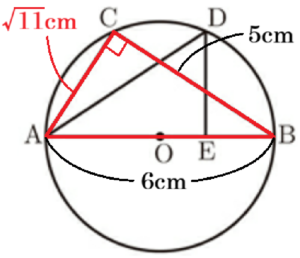
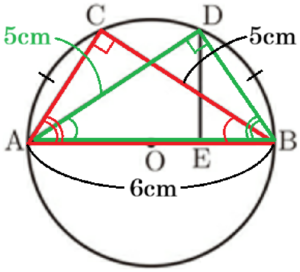
長さが \( 6 \; cm \) の線分 \( AB \) を直径とする円 \( O \) があります。図Ⅰのように,円 \( O \) の周上に,点 \( C \) を \( BC=5 \; cm \) となるようにとり,点 \( A \) と点 \( C \),点 \( B \) と点 \( C \) をそれぞれ結びます。また,点 \( A \) をふくまない方の \( \stackrel{\huge\frown}{ BC } \) 上に,点 \( D \) を \( \stackrel{\huge\frown}{ AC }=\stackrel{\huge\frown}{ BD } \) となるようにとり,点 \( A \) と点 \( D \) を結びます。さらに,点 \( D \) から線分 \( AB \) に垂線をひき,線分 \( AB \) との交点をEとします。
次の1~4の問いに答えなさい。
1 線分 \( AC \) の長さを求めなさい。
【解答】
\( AC=\sqrt{11} \; cm \)
【解説】
\( ∠ACB \) は直径 \( AB \) に対する円周角なので,
\( ∠ACB=90° \) であり,\( △ABC \) は直角三角形
になっています。
\( △ABC \) において三平方の定理より,
\( AC^2=AB^2-BC^2 \)
\( =6^2-5^2 \)
\( =11 \)
\( AC=\sqrt{11} \; (cm) \)( \( AC>0 \) より)
2 \( △ABC \) ∽ \( △DAE \) であることを証明しなさい。
【解答】
\( △ABC \) と \( △DAE \) において
\( ∠ACB \) は直径 \( AB \) に対する円周角なので,
\( ∠ACB=90° \) ・・・ ➀
仮定より,\( ∠DEA=90° \) ・・・ ➁
➀➁より,
\( ∠ACB=∠DEA \) ・・・ ➂
\( ∠ABC \) は \( \stackrel{\huge\frown}{ AC } \) に対する円周角,
\( ∠DAE \) は \( \stackrel{\huge\frown}{ BD } \) に対する円周角,
なので,\( \stackrel{\huge\frown}{ AC }=\stackrel{\huge\frown}{ BD } \) より,
\( ∠ABC=∠DAE \) ・・・ ➃
➂➃より,2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △DAE \)
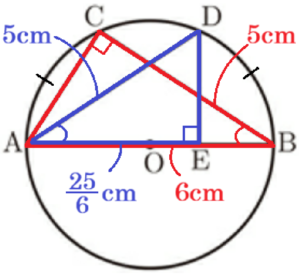
3 線分 \( AE \) の長さを求めなさい。
【解答】
\( AE=\dfrac{25}{6} \; cm \)
【解説】
\( △ABC \) と \( △BAD \) において,
\( ∠ADB \) は直径 \( AB \) に対する円周角なので,\( ∠BDA=90° \) であり,\( ∠ACB=∠BDA \)
問2より \( ∠ABC=∠BAD \) でもあるので,
\( ∠BAC=180°-(∠ACB+∠ABC) \)
\( ∠ABD=180°-(∠BDA+∠BAD) \)
より,\( ∠BAC=∠ABD \)
以上より,1組の辺とその間の角がそれぞれ等しいので,
\( △ABC≡△BAD \)
合同な図形の対応する辺の長さは等しいので,
\( AD=BC=5 \; cm \)
問2より \( △ABC \) ∽ \( △DAE \) であり,
対応する辺の比は等しいので,
\( AB:DA=BC:AE \)
\( 6:5=5:AE \)
\( 6AE=25 \)
\( AE=\dfrac{25}{6} \; (cm) \)
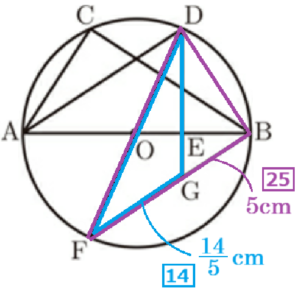
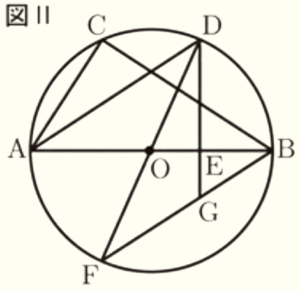
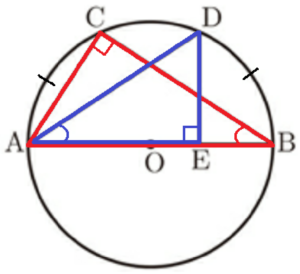
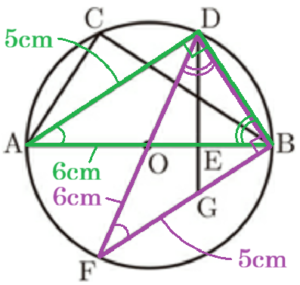
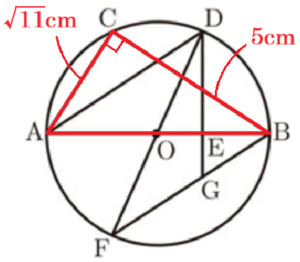
4 図Ⅱは,図Ⅰにおいて,直線 \( DO \) と円 \( O \) との交点のうち,\( D \) 以外の点を \( F \) とし,点 \( B \) と点 \( F \) を結んだものです。また,線分 \( DE \) を \( E \) の方に延長した直線と線分 \( BF \) との交点を \( G \) とします。\( △DFG \) の面積を求めなさい。
【解答】
\( △DFG=\dfrac{7\sqrt{11}}{5} \; cm^2 \)
【解説】
問3と同様の考え方で \( △DFB≡△BAD \) なので,
\( △DFB \) の面積と \( FG:FB \) を求めることで
\( △DFG \) の面積を求めることができます。
【\( △DFB \) の面積を求める】
問3と同様の考え方から \( △DFB≡△BAD≡△ABC \) なので,
\( △DFB \) と \( △ABC \) の面積は等しくなります。
(1)より,
\( BC=5 \; cm,AC=\sqrt{11} \; cm \)
なので,
\( △ABC=5 \times \sqrt{11} \times \dfrac{1}{2} \)
\( =\dfrac{5\sqrt{11}}{2} \; (cm^2) \)
よって,\( △DFB \) の面積は \( \dfrac{5\sqrt{11}}{2} \; cm^2 \)
【\( FB \) の長さを求める】
\( △DFB≡△BAD \) より,対応する辺の長さは等しいので,\( FB=AD=5 \; cm \) になります。
【\( FG \) の長さを求める】
\( △DAE \) ∽ \( △GBE \) であり,
\( AB=6 \; cm,AE=\dfrac{25}{6} \; cm \) より,
\( BE=AB-AE=\dfrac{11}{6} \; cm \)
対応する辺の比は等しいので,
\( AD:BG=AE:BE \)
\( 5:BG=\dfrac{25}{6}:\dfrac{11}{6} \)
\( 5:BG=25:11 \)
\( 25BG=55 \)
\( BG=\dfrac{11}{5} \; (cm) \)
\( FB=5 \; cm \) なので,
\( FG=FB-BG \)
\( =5-\dfrac{11}{5} \)
\( =\dfrac{14}{5} \; (cm) \)
\( \phantom{} \)
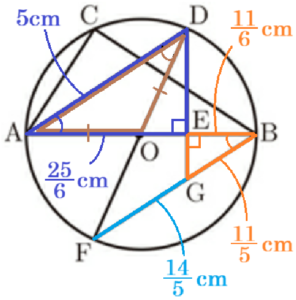
● \( △DAE \) ∽ \( △GBE \) の証明
\( △DAE \) と \( △GBE \) において,
\( \stackrel{\huge\frown}{ AF } \) に対する円周角なので,
\( ∠ODA=∠GBE \) ・・・ ➀
\( △ODA \) は二等辺三角形なので,
\( ∠EAD=∠ODA \) ・・・ ➁
➀➁より,
\( ∠EAD=∠GBE \) ・・・ ➂
\( DG⊥AB \) なので,
\( ∠DEA=∠GEB=90° \) ・・・ ➃
➂➃より,
2組の角がそれぞれ等しいので
\( △DAE \) ∽ \( △GBE \)
【\( △DFG \) の面積を求める】
\( △DFG \) の底辺を \( FG \),\( △DFB \) の底辺を \( FB \) とすると,高さが共通なので,
\( △DFB \) と \( △DFG \) の面積比は
\( FG:FB \) と等しくなります。
\( FG=\dfrac{14}{5} \; cm,FB=5 \; cm \) より,
\( FG:FB=\dfrac{14}{5}:5=14:25 \)
なので,\( △DFG \) の面積は,
\( △DFG=\dfrac{5\sqrt{11}}{2} \times \dfrac{14}{25}=\dfrac{7\sqrt{11}}{5} \; (cm^2) \)
\( \phantom{} \)