大問1
(1) \( -8-(-3) \) を計算しなさい。
【解説】
\( =-8+3 \)
\( =-5 \)
(2) \( -\dfrac{3}{7} \div \left(-\dfrac{9}{14} \right) \) を計算しなさい。
【解説】
\( =-\dfrac{3}{7} \times \left(-\dfrac{14}{9} \right) \)
\( =\dfrac{2}{3} \)
(3) 方程式 \( 5x+12=7x-4 \) を解きなさい。
【解説】
\( -2x=-16 \)
\( x=8 \)
(4) \( a=-5,b=\dfrac{1}{3} \) のとき,次の式の値を求めなさい。
\( 2(a-2b)-(5a-4b) \)
【解説】
与式 \( =2a-4b-5a+4b \)
\( =-3a \)
\( a=-5 \) を代入すると,
\( =-3 \times (-5) \)
\( =15 \)
(5) 二次方程式 \( x^2+4x-12=0 \) を解きなさい。
【解説】
\( (x-2)(x+6)=0 \)
\( x=2,-6 \)
(6) 3枚の10円硬貨を同時に投げるとき,2枚は表で,1枚は裏となる確率を求めなさい。
ただし,10円硬貨の表裏の出かたは,同様に確からしいとする。
【解説】
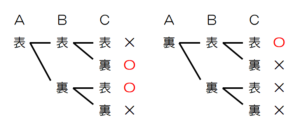
3枚の10円硬貨に「A」,「B」,「C」と名前をつけ,表裏の組み合わせを樹形図として書き出し,
2枚は表,1枚は裏となる組み合わせのところに ○ をつけると,
あてはまる組み合わせは3通り,すべての組み合わせは8通りなので,
求める確率は,\( \dfrac{3}{8} \)
【別の方法】
1枚だけが裏になるときなので,
「A」だけが裏のとき,「B」だけが裏のとき,「C」だけが裏のとき,の3通りがあてはまる
と考えれば,樹形図を書かなくても求められます。
(7) 次の標本調査について,標本の選び方として,最も適切なものを,次のア~エから1つ選び,記号で答えなさい。
ア 県内の中学生の1日の読書時間を調べるために,読書活動が盛んな中学校の生徒を無作為に抽出
して回答してもらった
イ 全国の高校生に人気のある曲を調べるために,回答をよびかけた自分のホームページを見て
くれた人に回答してもらった。
ウ ある工場では,製造しているお菓子の品質検査をするために,その日の最初に製造されたお菓子
\( 150 \) 個を検査した。
エ ある工場では,製造している電池が切れるまでの時間を調べるために,製造した電池の中から
\( 150 \) 個を無作為に抽出して検査した。
【解説】
標本調査する場合の標本の選び方は対象全体(母集団)の中から条件を設けずにランダムに選ぶ必要があります。
ア ・・・ 県内の中学生が対象になっているのに,読書活動が盛んな中学校に限定して選んでいるので,
適切ではない。
イ ・・・ 全国の高校生が対象になっているのに,回答者は自分のホームページを見てくれた人に限定されて
いるので,適切ではない。
(ホームページを見てくれた人には性別・趣味・興味などに偏りがあると考えられます)
ウ ・・・ 数時間にわたって製造を続けているのに,最初に製造したものに限定して検査しているので,
適切ではない。
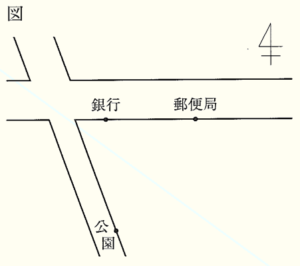
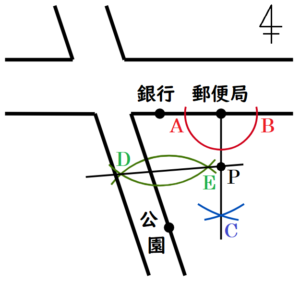
(8) 友子さんは, 右の図で,自分の家の位置を次のように説明した。
・ 私の家は,東西にのびている直線道路沿いにある
郵便局から,真南の方向にある。
・ 私の家は,銀行からも公園からも同じ距離にある。
友子さんの家の位置を点 \( P \) として,点 \( P \) をコンパスと定規を使って作図しなさい。作図に用いた線は消さずに残しておくこと。
ただし,図において,郵便局や銀行, 公園の位置は点 (・) で示しており,東西にのびている直線道路の幅は一定であるものとする。
【解答】
手順1 郵便局を中心に円弧を描く。
( 郵便局と銀行を通る横向きの線との
交点を \( A,B \) とします)
手順2 点 \(A,B \) を中心に円弧を描く。
(交点を \( C \) とします)
手順3 点 \( C \) と郵便局を通る直線を描く。
手順4 銀行と公園を中心に円弧を描く。
(交点を \( D,E \) とします)
手順5 点 \( D,E \) を通る直線を描く。
手順3と手順5の直線の交点が
求める点 \( P \) になります。
【解説】
1 点 \( P \) は,郵便局から,真南の方向にあるので,
東西にのびている直線道路に対する垂線(手順3の直線)上にあるとわかります。
2 点 \( P \) は,銀行からも公園からも同じ距離にあるので,
銀行と公園を通る直線の垂直二等分線(手順5の直線)上にあるとわかります。
1と2の直線の交点が求める点 \( P \) になります。
大問2
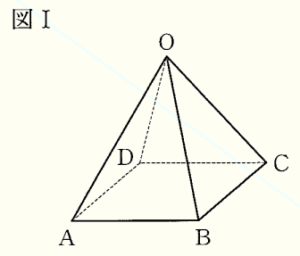
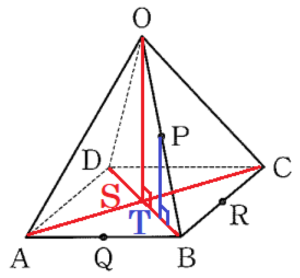
図Ⅰのような正四角錐 \( OABCD \) がある。底面 \( ABCD \) は1辺の長さが \( 4 \; cm \) の正方形で,他の辺の長さは,すべて \( 6 \; cm \) である。
このとき. 次の1~4の問いに答えなさい。
1 正四角錐 \( OABCD \) の展開図として正しくないものを,次のア~エから1つ選び,記号で答えなさい。
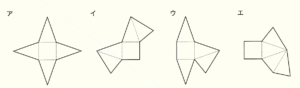
【解説】
ウの展開図を組み立てると,\( A \) の面と\( B \) の面が重なってしまいます。
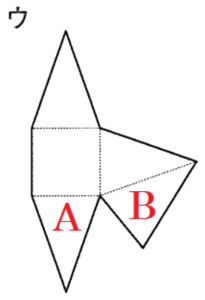
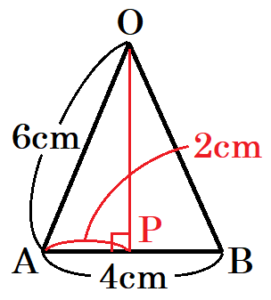
2 正四角錐 \( OABCD \) の側面積を求めなさい。
【解答】
\( 32\sqrt{2} \; cm^2 \)
【解説】
側面にあたる \( △OAB,△OBC,△OCD,△OAD \) は
すべて合同なので,\( △OAB \) の面積を求め,4倍します。
\( △OAB \) は \( OA=OB \) の二等辺三角形なので,
点 \( O \) から辺 \( AB \) に垂線をひき,交点を点 \( P \) とすると,
\( AP=\dfrac{1}{2}AB=2 \; (cm) \)
ここから,三平方の定理より,
\( OP^2=6^2-2^2=32 \)
\( OP=4\sqrt{2} \; (cm) \)
\( △OAB=4 \times 4\sqrt{2} \times \dfrac{1}{2}=8\sqrt{2} \; (cm^2) \)
よって,側面積は,
\( 8\sqrt{2} \times 4=32\sqrt{2} \; (cm^2) \)
3 正四角錐 \( OABCD \) の体積を求めなさい。
【解答】
\( \dfrac{32\sqrt{7}}{3} \; cm^3 \)
【解説】
点 \( O \) から面 \( ABCD \) に垂線をひき,
交点を点 \( S \) とすると,
点 \( S \) は,面 \( ABCD \) の対角線 \( AC \) の中点になります。
面 \( ABCD \) は1辺 \( 4 \; cm \) の正方形なので,
\( AC=4\sqrt{2} \; cm \) であり,
\( AS=\dfrac{1}{2}AC=2\sqrt{2} \; cm \)
\( △OAS \) において,三平方の定理より,
\( OS^2=6^2-(2\sqrt{2})^2=28 \)
\( OS=2\sqrt{7} \; (cm) \)
よって,正四角錐 \( OABCD \) の体積は,
\( (4 \times 4) \times 2\sqrt{7} \times \dfrac{1}{3}=\dfrac{32\sqrt{7}}{3} \; (cm^3) \)
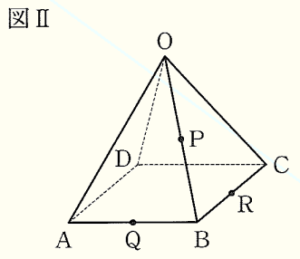
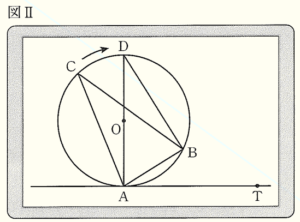
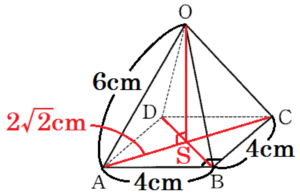
4 図Ⅱは,図Ⅰにおいて,辺 \( OB, AB, BC \) のそれぞれの中点 \( P,Q,R \) を示したものである。
このとき,4点 \( P,Q,B,R \) を頂点とする四面体 \( PQBR \) の体積を求めなさい。
【解答】
\( \dfrac{2\sqrt{7}}{3} \; cm^3 \)
【解説】
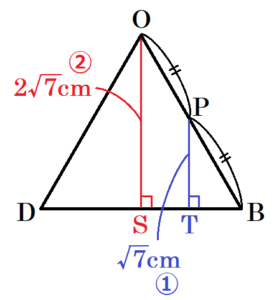
点 \( P \) から面 \( ABCD \) に垂線をひき,交点を点 \( T \) とすると,
点 \( S,T \) は,面 \( ABCD \) の対角線 \( BD \) 上の点になります。
面 \( OBD \) において,\( △OBS \) ∽ \( △PBT \) であり,
点 \( P \) は辺 \( OB \) の中点であることから,
\( OB:PB=2:1 \)
なので,
\( OS:PT=OB:PB \)
\( 2\sqrt{7}:PT=2:1 \)
\( PT=\sqrt{7} \; (cm) \)
点 \( Q,R \) は辺 \( AB,BC \) の中点であることから,\( BQ=BR=2 \; cm \) なので,
四面体 \( PQBR \) の体積は,
\( \left( 2 \times 2 \times \dfrac{1}{2} \right) \times \sqrt{7} \times \dfrac{1}{3}=\dfrac{2\sqrt{7}}{3} \; (cm^3) \)
大問3
裕一さんと真琴さんは,宮崎県の魅力を調べる中で,「日本のひなた宮崎県」というキャッチフレーズに興味をもった。2人は,宮崎県が温暖な気候であることに着目して,宮崎市の日照時間と日平均気温を調べることにした。
このとき,後の1,2の問いに答えなさい。
1 次の【会話Ⅰ】は,2人が日照時間について話し合っている場面である。後の(1)~(3)の問いに答えなさい。
【会話Ⅰ】
裕一:気象庁のデータをもとにして,宮崎市の日照時間をヒストグラムに表してみようよ。
真琴:そうだね。鹿児島市や大分市とも,くらべてみることにしよう。
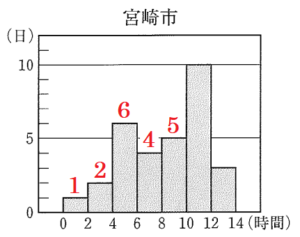
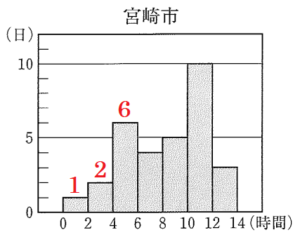
裕一:\( 2022 \) 年 \( 8 \) 月の日照時間をヒストグラムに表すと,図 I のようになったよ。
真琴:ヒストグラムを見ると,3つの市の日照時間のようすがよくわかるね。
裕一:宮崎市は,日照時間が \( 8 \) 時間以上の日が \( 18 \) 日あるから,他の市とくらべて日照時間が長いといえそう
だね。
真琴:ヒストグラムから最頻値や中央値を調べて,くらべてみようよ。
裕一:宮崎市の日照時間の最頻値は, ① 時間だから,3つの市の中で一番大きいね。
真琴:中央値をみると,鹿児島市と大分市は,同じ階級に含まれているね。宮崎市の中央値は, ➁ の階級
に含まれているよ。
裕一:ちなみに,日照時間の平均値は,宮崎市が一番大きいよ。
真琴:なるほど。調べた結果から,\( 2022 \) 年 \( 8 \) 月の日照時間は,宮崎市が3つの市の中で一番長いといえる
ね。
裕一:データをくらべやすくするために,箱ひげ図 もつくってみようよ。

(1) 【会話Ⅰ】の ① に当てはまる数を答えなさい。
【解説】
ヒストグラムにおいて,最頻値は「度数が最も大きい階級の階級値」になります。
度数が最も大きい階級は「\( 10 \) 時間以上 \( 12 \) 時間未満」であり,
この階級の階級値は,\( 10 \) 時間と \( 12 \) 時間の平均値なので,\( 11 \) 時間になります。
(2) 【会話Ⅰ】の ➁ に当てはまる階級を,次のア~エから1つ選び,記号で答えなさい。
ア \( 4 \) 時間以上 \( 6 \) 時間未満
イ \( 6 \) 時間以上 \( 8 \) 時間未満
ウ \( 8 \) 時間以上 \( 10 \) 時間未満
エ \( 10 \) 時間以上 \( 12 \) 時間未満
【解説】
\( 8 \) 月は \( 31 \) 日あるので,中央値になるのは,
日照時間の短い方から \( 16 \) 番目の日の値になります。
\( 8 \) 時間未満の度数の合計は
\( 1+2+6+4=13 \)(日)
で,
\( 8 \) 時間以上 \( 10 \) 時間未満の度数は \( 5 \)(日)なので,
短い方から \( 14 \) 番目から \( 18 \) 番目までの値が含まれます。
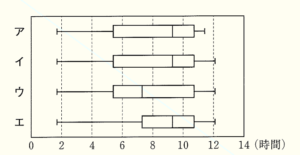
(3) 【会話Ⅰ】の 箱ひげ図 について,裕一さんは同じデータを使って,宮崎市の日照時間の箱ひげ図をつくった。宮崎市の日照時間を表す箱ひげ図として正しいものを,次のア~エから1つ選び,記号で答えなさい。
【解説】
(2)より,中央値は \( 8 \) 時間以上 \( 10 \) 時間未満の階級に含まれているので,
ウは正しくありません。
ヒストグラムより,最大値は \( 12 \) 時間以上 \( 14 \) 時間未満の階級に含まれているので,
アは正しくありません。
\( 8 \) 月は \( 31 \) 日あるので,第1四分位数になるのは,日照時間の短い方から \( 8 \) 番目の値になります。
短い方から \( 8 \) 番目の値は \( 4 \) 時間以上 \( 6 \) 時間未満の階級に含まれているので,
イ,エのうちあてはまるのはイになります。
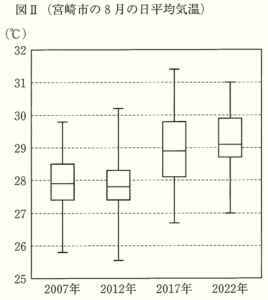
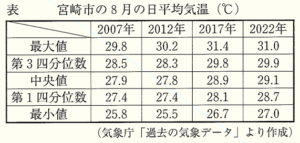
2 次に2人は,\( 2007 \) 年から \( 5 \) 年ごとに,宮崎市の \( 8 \) 月の日平均気温を調べ,表と図Ⅱのようにまとめた。【会話Ⅱ】は,表と図Ⅱを見ながら,日平均気温について話し合っている場面である。
このとき,下の(1),(2)の問いに答えなさい。
【会話Ⅱ】
真琴:箱ひげ図は,データのおおまかな分布のようすをとらえることができるね。
裕一:四分位範囲が一番小さいのは, 年の箱ひげ図だね。
真琴:そうだね。\( 2007 \) 年と \( 2022 \) 年の箱ひげ図をくらべて,\( 8 \) 月の日平均気温について,どんなことがいえるか考えてみようよ。
裕一:表の最大値と最小値に着目すると,どちらの年も範囲が同じであることがわかるね。
真琴:範囲は同じだけど,箱ひげ図を見ると,日平均気温は \( 2007 \) 年より \( 2022 \) 年の方が高い傾向にあるといえるね。
(1) 【会話Ⅱ 】の に当てはまる年を答えなさい。
【解説】
四分位範囲は,「第3四分位数 \( – \) 第1四分位数」で求められます。
各年の四分位範囲は,
\( 2007 \) 年 ・・・ \( 28.5-27.4=1.1 \) (℃)
\( 2012 \) 年 ・・・ \( 28.3-27.4=0.9 \) (℃)
\( 2017 \) 年 ・・・ \( 29.8-28.1=1.7 \) (℃)
\( 2022 \) 年 ・・・ \( 29.9-28.7=1.2 \) (℃)
なので,一番小さいのは \( 2012 \) 年 になります。
(2) 【会話Ⅱ】の波線部のように,「日平均気温は,\( 2007 \) 年より \( 2022 \) 年の方が高い傾向にある」と主張することができます。このように主張することができる理由を,「第1四分位数」と「第3四分位数」の両方の言葉を用いて説明しなさい。
【解答】
\( 2007 \) 年の第1四分位数と \( 2022 \) 年の第1四分位数,
\( 2007 \) 年の第3四分位数と \( 2022 \) 年の第3四分位数
をそれぞれ比較すると,どちらも\( 2022 \) 年の値の方が大きいから
【解説】
箱ひげ図の箱の部分には,全体の約 \( 50 \% \) の値が含まれます。
この問題の場合では,\( 17 \) 日分の値が箱の中に含まれます。
\( 2007 \) 年の場合,\( 1 \) か月の日平均気温のうち,
\( 17 \) 日がおよそ \( 27.3 \) ℃から \( 28.5 \) ℃の範囲の値であったのに対し,
\( 2022 \) 年の場合,\( 1 \) か月の日平均気温のうち,
\( 17 \) 日がおよそ \( 28.7 \) ℃から \( 29.9 \) ℃の範囲の値だったことになります。
ここから,\( 2007 \) 年より \( 2022 \) 年の方が高い傾向にあるといえます。
大問4
美織さんと正樹さんは,数学の授業で,タブレット端末を使って図形をつくった。図Ⅰは,下の【設定】にしたがってつくった図形を,表示したものである。
このとき,後の1~3の各問いに答えなさい。
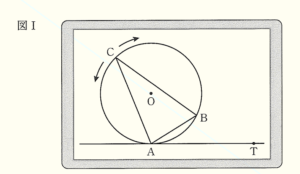
【設定】
・ 円 \( O \) の円周上に3点 \( A,B,C \) をとり,\( △ABC \) をつくる。
・ 2点 \( A,B \) は固定し,点 \( C \) は半円の弧より長い 弧 \( AB \) 上を自由に動かすことができる。
・ 点 \( C \) は,2点 \( A,B \) には重ならない。
・ 点 \( A \) を接点とする円 \( O \) の接線をひき,接線上に点 \( A \) と異なる点 \( T \) をとる。
ただし,点 \( T \) は,点 \( A \) の右側にあるものとする。
1 【会話Ⅰ】は,2人が,点 \( C \) を動かしながら図形の性質や関係について話し合っている場面である。
【会話Ⅰ】
美織:点 \( C \) を動かすと,\( △ABC \) の形が変わるから,辺 \( CA \),辺 \( CB \) の長さが変わるね。
正樹:角については,どんなことがいえるかな。
美織:円周角の定理が成り立つから,\( ∠ACB \) の大きさは点 \( C \) がどの位置にあっても同じよ。
正樹:そうだね。2点 \( A,B \) は固定されているから,\( ∠BAT \) の大きさもいつも同じだね。
美織:なるほど。点 \( C \) をどの位置に動かしても,\( ∠ACB \) と \( ∠BAT \) の大きさは変わらないとうことね。
正樹:\( ∠ACB \) と \( ∠BAT \) の大きさは等しいのかな。
美織:見た目には等しく見えるけど,詳しく調べてみようよ。
2人は,\( ∠ACB \) と \( ∠BAT \) について,次のことを予想した。
【予想】 点 \( C \) をどの位置に動かしても,\( ∠ACB=∠BAT \) が成り立つ。
この【予想】が成り立つことを証明するために,図Ⅱのように線分 \( CA \) が円 \( O \) の直径となるように点 \( C \) を点 \( D \) の位置まで動かした。次の【証明】の ア ~ ウ に当てはまる記号や式,角度を書きなさい。
ただし,同じカタカナのところには共通するものが入る。
【証明】
\( ∠ACB \) と \( ∠ADB \) は,どちらも ア に
対する円周角だから,円周角の定理より,
\( ∠ACB=∠ADB \) ・・・ ①
直線 \( AT \) は円 \( O \) の接線だから,
\( ∠DAT= \) イ
これより,
\( ∠BAT= \) ウ ・・・ ➁
半円の弧に対する円周角であるから,
円周角の定理より,
\( ∠ABD= \) イ
これより,
\( ∠ADB= \) ウ ・・・ ③
②,③から,
\( ∠BAT=∠ADB \) ・・・ ➃
したがって,①,④から,
\( ∠ACB=∠BAT \)
【解答】
ア ・・・ \( \overset{\frown}{AB} \)
イ ・・・ \( 90° \)
ウ ・・・ \( 90°-∠BAD \)
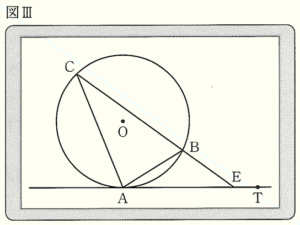
2 図Ⅲは,図Ⅰにおいて,点 \( C \) を固定し,線分 \( CB \) を延長した直線と直線 \( AT \) との交点を \( E \) としたものである。このとき,2人は,\( △CAE \) ∽ \( △ABE \) であると予想した。次の【会話Ⅱ】は,その予想が成り立つことを確認している場面である。【会話Ⅱ】の エ には式を, オ には当てはまる言葉を書きなさい。
【会話Ⅱ】
美織:\( △CAE \) ∽ \( △ABE \) を確認しようよ。
正樹:\( △CAE \) と \( △ABE \) で,2つの三角形に
共通な角だから, エ だね。
美織:そして,さっき証明したことから,
\( ∠ACE=∠BAE \) がいえるね。
正樹:\( △CAE \) と \( △ABE \) で, オ ので,
\( △CAE \) ∽ \( △ABE \) が成り立つね。
美織:これを利用して,いろいろな問題を考えて
みよう。
【解答】
エ ・・・ \( ∠AEC=∠BEA \)
オ ・・・ 2組の角がそれぞれ等しい
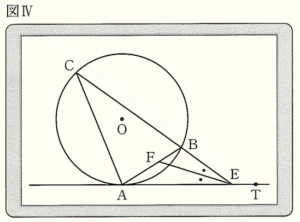
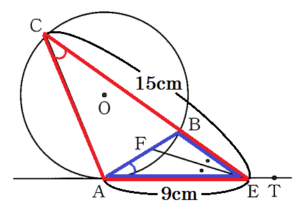
3 図Ⅳは,図Ⅲにおいて,\( ∠AEC \) の二等分線をひき,線分 \( AB \) との交点を \( F \) としたものである。\( AE=9 \; cm,CE=15 \; cm \) のとき,次の(1),(2)の問いに答えなさい。
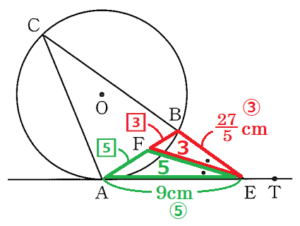
(1) 線分 \( BE \) の長さを求めなさい。
【解答】
\( \dfrac{27}{5} \; cm \)
【解説】
\( △CAE \) ∽ \( △ABE \) なので,
\( AE:BE=CE:AE \)
\( 9:BE=15:9 \)
\( 15BE=81 \)
\( BE=\dfrac{27}{5} \; (cm) \)
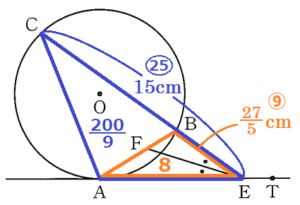
(2) \( △BFE \) の面積は,\( △CAE \) の面積の何倍になりますか。
【解答】
\( \dfrac{27}{200} \) 倍
【解説】
線分 \( EF \) は,\( ∠AEC \) の二等分線なので,
\( BF:FA=BE:AE=\dfrac{27}{5}:9=3:5 \)
\( △BEF \) と \( △AEF \) は高さが共通なので,
\( △BEF:△AEF=BF:FA=3:5 \)
ここから,\( △BEF \) の面積を「3」とすると,
\( △AEF \) の面積は「5」
\( △ABE \) の面積は「8」
と表すことができます。
\( △ABE \) と \( △CAE \) は高さが共通で,
\( BE=\dfrac{27}{5} \; cm,CE=15 \; cm \) なので,
\( △ABE:△CAE=\dfrac{27}{5}:15=9:25 \)
ここから,
\( △ABE:△CAE=9:25 \)
\( 8:△CAE=9:25 \)
\( △CAE=\dfrac{200}{9} \)
となり,
\( △CAE \) の面積は「\( \dfrac{200}{9} \)」
と表すことができます。
以上より,
\( △BEF:△CAE=3:\dfrac{200}{9} \)
\( \dfrac{200}{9}△BEF=3△CAE \)
\( △BEF=\dfrac{27}{200}△CAE \)
なので,\( △BFE \) の面積は,\( △CAE \) の面積の \( \dfrac{27}{200} \) 倍
大問5
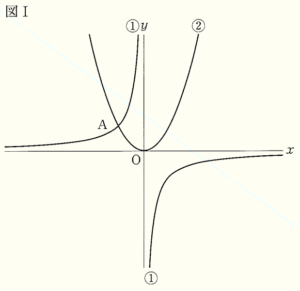
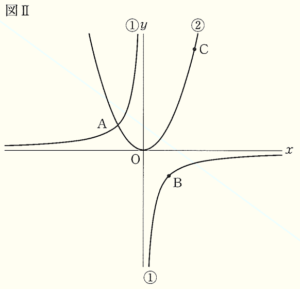
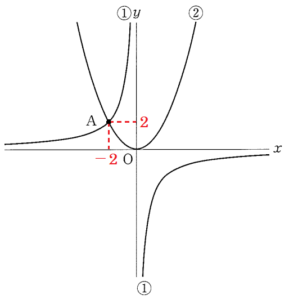
図Ⅰのように,2つの関数
\( y=\dfrac{a}{x} \;\; (a<0) \) ・・・ ①
\( y=\dfrac{1}{2}x^2 \) ・・・ ➁
のグラフが点 \( A \) で交わっている。点 \( A \) の \( x \) 座標は \( -2 \) である。
このとき,次の1~3の問いに答えなさい。
1 関数①と②に共通する特徴を述べた文として正しいものを,次のア~エから1つ選び,記号で答えなさい。
ア グラフは,\( y \) 軸を対称の軸として線対称である。
イ 対応する \( x \) と \( y \) の値の積 \( xy \) は一定である。
ウ 変化の割合は一定ではない。
エ \( x<0 \) で,\( x \) の値が増加するにつれて,\( y \) の値は増加する。
【解説】
ア ・・・ ① のグラフは,線対称にはなっていないので正しくない。
イ ・・・ ➁(二次関数) のグラフでは,\( xy \) の値は一定にはならないので,正しくない。
| \( y=\dfrac{1}{2}x^2 \) の場合 |
| \( x \) |
\( 0 \) |
\( 1 \) |
\( 2 \) |
\( 3 \) |
・・・ |
| \( y \) |
\( 0 \) |
\( \dfrac{1}{2} \) |
\( 2 \) |
\( \dfrac{9}{2} \) |
・・・ |
| \( xy \) |
\( 0 \) |
\( \dfrac{1}{2} \) |
\( 4 \) |
\( \dfrac{27}{2} \) |
・・・ |
ウ ・・・ 下の図において,赤の部分の変化の割合(傾き)と青の部分の変化の割合(傾き)は明らかに異なっているので,
正しい。
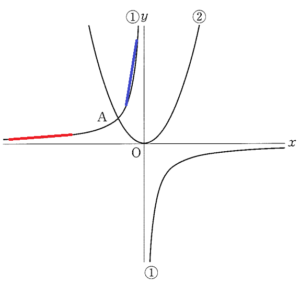
エ ・・・ ➁ のグラフでは,\( x<0 \) で,\( x \) の値が増加するにつれて,\( y \) の値は減少しているので,
正しくない。
2 \( a \) の値を求めなさい。
【解説】
点 \( A \) は,\( y=\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標は \( -2 \) なので,\( y \) 座標は,
\( y=\dfrac{1}{2} \times (-2)^2=2 \)
\( y=\dfrac{a}{x} \) に \( x=-2,y=2 \) を代入すると,
\( 2=\dfrac{a}{-2} \)
\( a=-4 \)
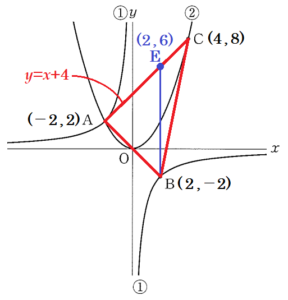
3 図Ⅱは,図Ⅰにおいて,① のグラフ上に点 \( B \) を,② のグラフ上に点 \( C \) をとったものである。点 \( B,C \) の \( x \) 座標はそれぞれ,\( 2,4 \) である。
このとき,次の(1),(2)の問いに答えなさい。
(1) \( △ABC \) の面積を求めなさい。
【解説】
点 \( B \) は,\( y=-\dfrac{4}{x} \) 上の点で,
\( x \) 座標は \( 2 \) なので,\( y \) 座標は,
\( y=-\dfrac{4}{2}=-2 \)
であり,\( B(2,-2) \)
点 \( C \) は,\( y=\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標は \( 4 \) なので,\( y \) 座標は,
\( y=\dfrac{1}{2} \times 4^2=8 \)
であり,\( C(4,8) \)
直線 \( AC \) の式を \( y=ax+b \) とすると,\( A(-2,2),C(4,8) \) を通ることから,
傾き \( a=\dfrac{8-2}{4-(-2)}=1 \)
\( y=x+b \) に \( x=4,y=8 \) を代入すると,
\( 8=4+b \)
\( b=4 \)
となり,直線 \( AC \) の式は \( y=x+4 \)
点 \( B \) を通り,\( y \) 軸に平行な直線と直線 \( AC \) との交点を点 \( E \) とすると,
点 \( E \) の \( x \) 座標は \( 2 \) なので,\( y \) 座標は,
\( y=2+4=6 \)
であり,\( E(2,6) \)
以上より,\( △ABC \) の面積は,
\( △ABC=△ABE+△CBE \)
\( =\left( 8 \times 4 \times \dfrac{1}{2} \right)+\left( 8 \times 2 \times \dfrac{1}{2} \right) \)
\( =16+8 \)
\( =24 \)
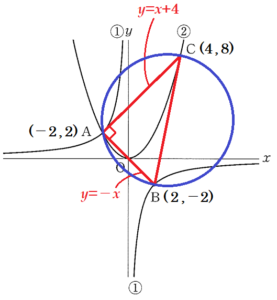
(2) 3点 \( A,B,C \) を通る円の面積を求めなさい。
ただし,円周率は \( \pi{} \) とする。
【解説】
直線 \( AB \) の式を \( y=ax+b \) とすると,\( A(-2,2),B(2,-2) \) を通ることから,
傾き \( a=\dfrac{-2-2}{2-(-2)}=-1 \)
\( y=-x+b \) に \( x=2,y=-2 \) を代入すると,
\( -2=-2+b \)
\( b=0 \)
となり,直線 \( AB \) の式は \( y=-x \)
直線 \( AB \) の式の傾きは \( -1 \),
直線 \( AC \) の式の傾きは \( 1 \)
であり,かけて \( -1 \) になることから,
直線 \( AB \) と直線 \( AC \) は垂直に交わっています。
\( ∠BAC=90° \) は,3点 \( A,B,C \) を通る円の円周角になっているので,
線分 \( BC \) は,直径になっているとわかります。
直径 \( BC \) の長さは,
\( BC^2=2^2+10^2=104 \)
\( BC=2\sqrt{26} \)
ここから,3点 \( A,B,C \) を通る円の面積は,
\( \dfrac{\pi{}}{4} \times (2\sqrt{26})^2=\dfrac{\pi{}}{4} \times 4 \times 26=26\pi{} \)