大問１
(1) \( -3+4 \) を計算しなさい。
(2) \( n \) を負の整数としたとき，計算結果がいつでも正の整数になる式を，次の ア～エ から１つ選び，記号を書きなさい。
〔 ア \( 5+n \) イ \( 5-n \) ウ \( 5 \times n \) エ \( 5 \div n \) ］
(3) \( \dfrac{3x-5y}{2}-\dfrac{2x-y}{4} \) を計算しなさい。
(4) \( (x-3)^2+2(x-3)-15 \) を因数分解しなさい。
(5) 二次方程式 \( x^2+2x-1=0 \) を解きなさい。
(6) \( 12 \; m \) のロープを \( x \) 等分したときの，１本分のロープの長さを \( y \; m \) とする。\( x \) と \( y \) の関係についていえることを，次の ア～エ から２つ選び，記号を書きなさい。
ア \( x \) の値が \( 2 \) 倍，\( 3 \) 倍，\( 4 \) 倍，･･･ になると，\( y \) の値も \( 2 \) 倍，\( 3 \) 倍，\( 4 \) 倍, ･･･ になる。
イ \( x \) の値が \( 2 \) 倍，\( 3 \) 倍，\( 4 \) 倍，･･･ になると，yの値は\( \dfrac{1}{2} \) 倍，\( \dfrac{1}{3} \) 倍，\( \dfrac{1}{4} \) 倍，･･･ になる。
ウ 対応する \( x \) と \( y \) の値の積 \( xy \) は一定である。
エ 対応する \( x \) と \( y \) の値の商 \( \dfrac{y}{x} \) は一定である。
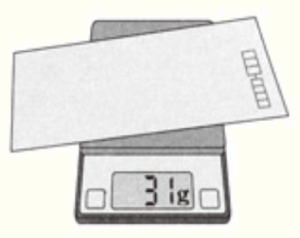
(7) ある郵便物の重さをデジタルはかりで調べたところ，\( 31 \; g \) と表示された。
この数値は小数第１位を四捨五入して得られた値である。この郵便物の
重さの真の値を \( a \; g \) としたとき，\( a \) の範囲を不等号を使って表したものとして正しいものを，次の ア～エ から１つ選び，記号を書きなさい。
ア \( 30.5<a<31.5 \) イ \( 30.5≦a≦31.5 \)
ウ \( 30.5≦a<31.5 \) エ \( 30.5<a≦31.5 \)
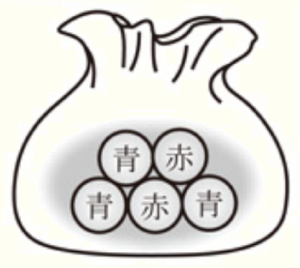
(8) 赤玉２個，青玉３個が入っている袋がある。この袋から，玉を１個取り出し，それを袋に戻さないで，続けて玉を１個取り出す。
このとき，取り出した２個の玉の色が異なる確率を求めなさい。
ただし，どの玉が取り出されることも同様に確からしいものとする。
２個の玉の色が異なる組み合わせのところに ○ をつけると，下の図のようになります。
すべての組み合わせは２０通り，色が異なる組み合わせは１２通りなので，
求める確率は，\( \dfrac{12}{20}=\dfrac{3}{5} \)
ちなみに，同時に取り出していないので，こんな樹形図にはなりません。
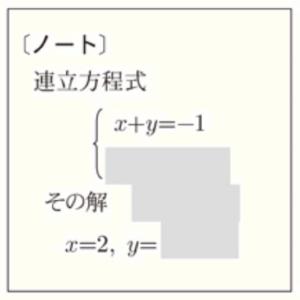
(9) ノートには，ある連立方程式とその解が書かれていたが，一部が消えてしまった。消えてしまった二元一次方程式はどれか，次の ア～エ から１つ選び，記号を書きなさい。
ア \( x-y=-1 \) イ \( 3x-2y=10 \)
ウ \( x+4y=10 \) エ \( x-3y=11 \)
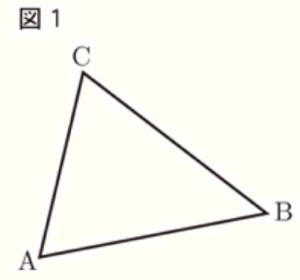
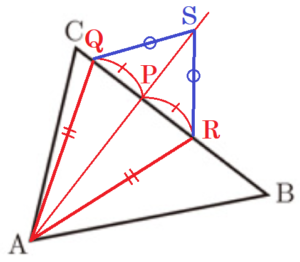
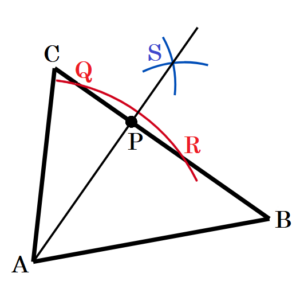
(10) 図１のように，\( △ABC \) がある。辺 \( BC \) 上に，\( BC⊥AP \) となる点 \( P \) を，定規とコンパスを使って作図しなさい。ただし，点 \( P \) を表す文字 \( P \) も書き，作図に用いた線は消さないこと。
（辺 \( BC \) との交点を点 \( Q，R \) とします。）
手順２ 点 \( Q，R \) を中心に円弧を描く。
（交点を点 \( S \) とします。）
手順３ ２点 \( A，S \) を通る直線を描く。
手順３の直線と辺 \( BC \) の交点が求める点 \( P \) になります。
二等辺三角形の頂角から底辺に垂線をひくと，
この垂線は底辺の垂直二等分線になることを利用します。
点 \( A \) からの距離が等しくなるような２点 \( Q，R \) を
辺 \( BC \) 上にとると，\( △AQR \) は二等辺三角形になります。
さらに，２点 \( Q，R \) からの距離が等しくなる点 \( S \) を作図すると，
\( △SQR \) も二等辺三角形になるので，\( BC⊥AS \) になります。
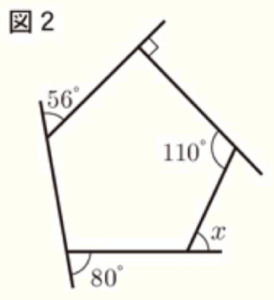
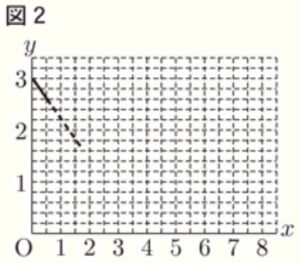
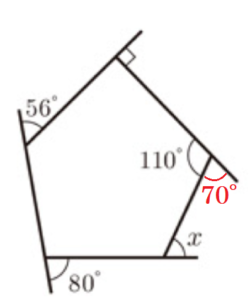
(11) 図２において，\( ∠x \) の大きさを求めなさい。
\( 360°-(56°+90°+70°+80°)=64° \)
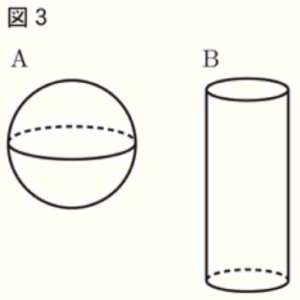
(12) 図３は，半径が \( 3 \; cm \) の球 \( A \) と底面の半径が \( 2 \; cm \) の
円柱 \( B \) である。\( A \) と \( B \) の体積が等しいとき，\( B \) の高さ
を求めなさい。
大問２
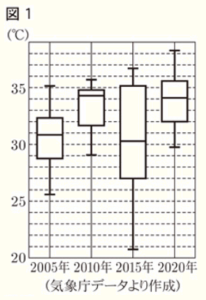
Ⅰ 守さんは，Ａ市について２００５年，２０１０年，２０１５年，２０２０年の８月の日最高気温（その日の最も高い気温）を調べ，どのような傾向にあるか考えるため，図１の箱ひげ図に表した。
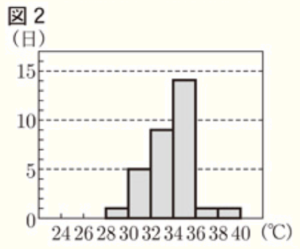
(1) 図２は，図１のいずれかの年の箱ひげ図をつくる際にもとにしたデータを，ヒストグラムに表したものである。図２は，何年のヒストグラムか書きなさい。
(2) 図１から読みとれることとして，次の ➀，➁ は，「正しい」，「正しくない」，「図１からはわからない」のどれか，最も適切なものを，下の ア～ウ から１つずつ選び，記号を書きなさい。
➀ ２０２０年は，８月の日最高気温の散らばりが，４つの箱ひげ図の中で２番目に小さい。
➁ ２００５年は，８月の日最高気温が３５℃を超えた日は１日しかない。
〔 ア 正しい イ 正しくない ウ 図１からはわからない 〕
(3) 図１で，２０１０年と２０１５年の８月の日最高気温の分布を比較して次のようにまとめた。 あ ， い に当てはまる最も適切なものを，下の ア～エ から１つずつ選び，記号を書きなさい。
ただし， あ ， い には異なる記号が入る。
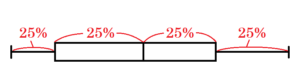
最大値を比べると，２０１５年は２０１０年よりも高いことがわかる。しかし，２０１５年は，全体の あ 以上の日が３０℃を超えていたが，２０１０年は，全体の あ 以上の日が３４℃を超えていた。また，２０１０年の最小値は約２９℃であるが，２０１５年は，全体の約 い の日が ２７℃以下であり，２０１５年は２０１０年と比べて，日最高気温の低い日が多かったことがわかる。
〔 ア ２５% イ ５０% ウ ７５% エ １００% 〕
上下のひげの部分，第二四分位数をはさんで箱の左右には，それぞれ約 \( 25 \)％のデータが含まれます。
よって，中央値から最大値までの間には約 \( 50 \)％のデータ，
最小値から第一四分位数までの間には約 \( 25 \)％のデータが含まれることになります。
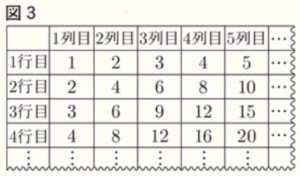
Ⅱ 春さんは，自然数をある規則に従って並べ，表にまとめた。図３はその一部である。春さんは咲さんに，表を用いて，次のような数あてマジックを行った。
春：表の中から１つ数を選んでください。その数は表の何行目にありますか?
咲：３行目だよ。
春：選んだ数とその右隣の数，さらにその右隣の数の３つの数をたすといくつになりますか?
咲：\( 27 \) だよ。
春：最初に選んだ数は・・・，表の３行目の２列目にある６ですね。
咲：あたり！ どうしてわかったの？
(1) 春さんは，数あてマジックの仕組みとその説明を咲さんに示すため，ノート１にまとめた。
に途中の過程を書き，正しい説明を完成させなさい。
〔ノート１〕
最初に選んだ数を \( a \)，\( a \) の右隣の数を \( b \)，\( b \) の右隣の数を \( c \) とする。
➀ ３つの数 \( a，b，c \) の和を \( 3 \) でわると \( b \) がわかる。
➁ \( a \) が \( m \) 行目の数であるとき，\( b \) から \( m \) をひくと，最初に選んだ数 \( a \) がわかる。
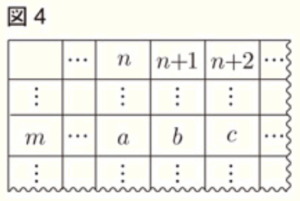
数あてマジックの仕組みの ➀ について，図４のように，\( a \) を \( m \) 行目，\( n \) 列目の数とし，
\( a+b+c \) と \( 3b \) が等しくなることを，\( m，n \) を用いて説明する。
\( a=mn，b=m(n+1) ，c=m(n+2) \) と表されるから，
数あてマジックの仕組みの ➁ について，\( b \) から \( m \) をひくと，
\( b-m=m(n+1)-m=mn+m-m=mn \) である。\( a=mn \) より，\( b-m=a \) である。
(2) 春さんは，表において，横に連続して並ぶ５つの数についても，同じような関係が成り立つことに気づき，ノート２にまとめた。ノート２が正しくなるように， う ， お には当てはまる適切な数を， え には \( a，b，c，d，e \) のいずれかの文字１つをそれぞれ書きなさい。
〔ノート2〕
最初に選んだ数を \( a \)，\( a \) の右隣の数を \( b \)，\( b \) の右隣の数を \( c \)，\( c \) の右隣の数を \( d \)，\( d \) の右隣の数を \( e \) とする。５つの数 \( a，b，c，d，e \) の和を う でわると え がわかる。
表の１１行目にある数のうち，横に連続して並ぶ５つの数の和が \( 605 \) である。このとき，最初に選んだ数 \( a \) は お である。
大問３
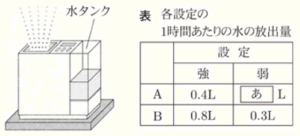
Ⅰ 秋さんの家には，水の放出量が異なる2つの加湿器Ａ，Ｂがある。Ａ，Ｂにはともに「強」，「弱」の２つの設定があり，各設定の１時間あたりの水の放出量は表のとおりである。
ただし，Ａ，Ｂのどの設定もそれぞれ一定の割合で水を放出し，放出された水の量だけ水タンクから水が減るものとする。
(1) 秋さんは，まずＡを使ってみた。水タンクに \( 2 \; L \) の水を入れた状態から「弱」の設定で運転し，\( 4 \) 時間後に「強」の設定に切り替えたところ，運転開始からちょうど \( 7 \) 時間後に水タンクの水がなくなった。
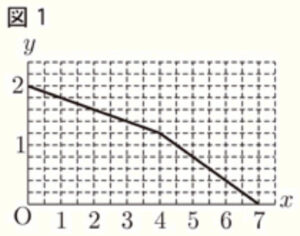
図１は，運転開始から \( x \) 時間後の水タンクの水の量を \( y \; L \) として，\( x \) と \( y \) の関係を表したグラフである。
➀ 表の あ に当てはまる適切な数を求めなさい。
➁ \( x \) の変域が \( 4≦x≦7 \) のとき，\( x \) と \( y \) の関係を式に表しなさい。
(2) 秋さんは，次にＢを使った。Ｂには，室内が一定の湿度に達すると「強」から「弱」の設定に自動で切り替わる機能がある。水タンクに \( 3 \; L \) の水を入れた状態から「強」の設定で運転し，途中で「弱」の設定に自動で切り替わり，そのまま「弱」の設定で運転を続けたところ，運転開始からちょうど \( 8 \) 時間後に水タンクの水がなくなった。秋さんは，Ｂの運転開始からの時間と水タンクの水の量について，次のようにまとめた。
〔秋さんがまとめたこと〕
Ｂの運転開始から \( x \) 時間後の水タンクの水の量を \( y \; L \) として，図２に水の量の変化をかき入れる。
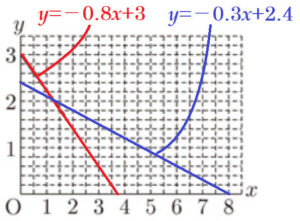
まず，\( y \) 軸上の点 \( \underline{(0，3)} \) を通り，傾き \( \underline{-0.8} \) の直線をひく。
次に， い の直線をひく。
このとき，この２本の直線の う の え 座標は，「強」から「弱」の設定に切り替わった時間を表している。
➀ 秋さんがまとめたことが正しくなるように， い に当てはまる適切な言葉を，秋さんがまとめたことの下線部のように座標と傾きを具体的に示して書きなさい。また， う には当てはまる適切な語句を， え には当てはまる適切な文字を，それぞれ書きなさい。
➁ Ｂの設定が「強」から「弱」に切り替わったのは，運転開始から何時間何分後か，求めなさい。
赤の直線の式は \( y=-0.8x+3 \)，
青の直線の式は \( y=-0.3x+2.4 \)
なので，
\( \left\{ \begin{array}{}
y=-0.8x+3 \; ･･･ ① \\
y=-0.3x+2.4 \; ･･･ ➁ \\
\end{array} \right. \)
\( -0.8x+3=-0.3x+2.4 \)
\( 0.5x=0.6 \)
\( x=\dfrac{6}{5}=1+\dfrac{1}{5} \) （時間）
\( \dfrac{1}{5} \) 時間 \( =\dfrac{1}{5} \times 60=12 \) 分なので，
求める時間は，\( 1 \) 時間 \( 12 \) 分後
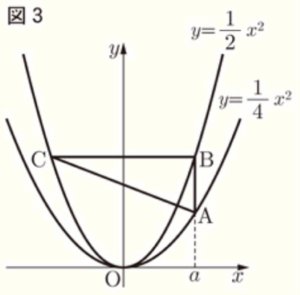
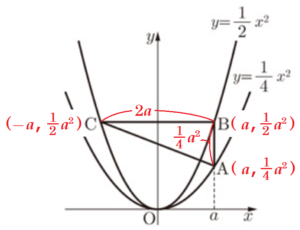
Ⅱ 図３は，関数 \( y=\dfrac{1}{4}x^2 \) のグラフ上に，\( x \) 座標が正の数 \( a \) である点 \( A \) をとり，関数 \( y=\dfrac{1}{2}x^2 \) のグラフ上に，点 \( A \) と \( x \) 座標が等しい点 \( B \) と，点 \( B \) と \( y \) 軸について対称な点 \( C \) をとり，\( △ABC \) をつくったものである。
(1) \( a=4 \) のとき，\( AB \) の長さを求めなさい。
(2) \( AB \) と \( BC \) の長さが等しくなるとき，\( a \) の値を求めなさい。
(1) と同様に考えると，
\( x=a \) のときの点 \( A，B \) の \( y \) 座標の値は，
点 \( A \) の場合が \( y=\dfrac{1}{4}a^2 \)，
点 \( B \) の場合が \( y=\dfrac{1}{2}a^2 \)
となるので，
\( AB=\dfrac{1}{2}a^2-\dfrac{1}{4}a^2=\dfrac{1}{4}a^2 \)
また，\( y=\dfrac{1}{2}x^2 \) のグラフは，
\( y \) 軸について対称なので，
点 \( B，C \) の \( y \) 座標は等しいことから，
点 \( C \) の \( x \) 座標は，\( x=-a \) となります。
よって，\( BC=a-(-a)=2a \)
\( AB=BC \) より，
\( \dfrac{1}{4}a^2=2a \)
\( a^2=8a \)
\( a(a-8)=0 \)
\( a=8 \) (\( a \) は正の数のため)
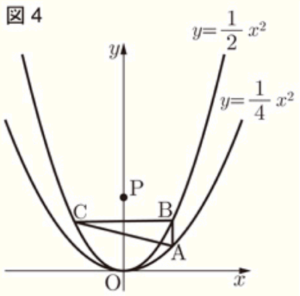
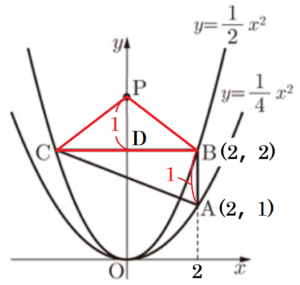
(3) 図４は，図３において \( a=2 \) とし，\( y \) 軸上に，\( y \) 座標が \( 2 \) より大きい点 \( P \) をとったものである。
➀ \( △BCP \) の面積が，\( △ABC \) の面積と等しくなるとき，点 \( P \) の座標を求めなさい。
線分 \( BC \) と \( y \) 軸の交点を点 \( D \) とすると，
\( △BCP \) の高さは \( PD \)，\( △ABC \) の高さは \( AB \) になります。
\( a=2 \) のとき，
点 \( A \) の座標は \( A(2，1) \)，
点 \( B \) の座標は \( B(2，2) \)
なので，\( AB=1 \)
点 \( D \) の \( y \) 座標は，点 \( B \) と等しいので，\( 2 \)
よって，点 \( D \) の座標は，\( D(0，2) \)
点 \( P \) は，\( y \) 座標が \( 2 \) より大きく，
\( PD=1 \) となる点なので，\( P(0，3) \)
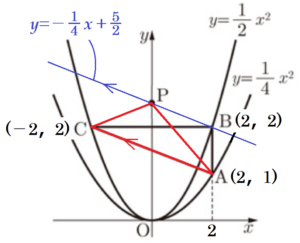
➁ \( △ACP \) の面積が，\( △ABC \) の面積と等しくなるとき，点 \( P \) の座標を求めなさい。
つまり，等積変形の考え方から，\( AC//BP \) となるときの直線 \( BP \) の切片が点 \( P \) になります。
\( a=2 \) のとき，
点 \( A \) の座標は \( A(2，1) \)，
点 \( C \) の座標は \( C(-2，2) \)
なので，直線 \( AC \) の傾きは，
傾き \( =\dfrac{1-2}{2-(-2)}=-\dfrac{1}{4} \)
平行な直線の傾きは等しいので，
直線 \( BP \) の式を \( y=-\dfrac{1}{4}x+b \) とすると，\( B(2，2) \) を通るので，
\( 2=-\dfrac{1}{4} \times 2+b \)
\( b=\dfrac{5}{2} \)
よって，\( P \left (0，\dfrac{5}{2} \right) \)
大問４
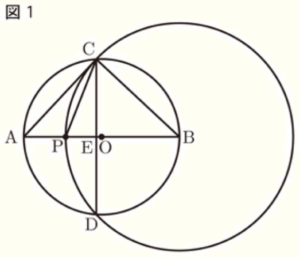
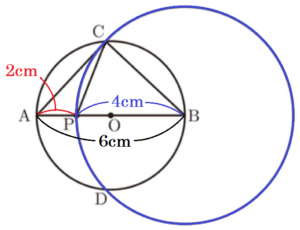
点を動かしたり，図形の大きさを変えたりすることができる数学の作図ソフトがある。桜さんは，その作図ソフトを使って，次の 作図の手順 に従って図１をかき，点 \( P \) を線分 \( AB \) 上で，点 \( A \) から点 \( B \) の向きに動かしたときの図形を観察した。
〔作図の手順〕
１ 長さが \( 6 \; cm \) の線分 \( AB \) を直径とする円 \( O \) を
かく。
２ 線分 \( AB \) 上に点 \( P \) をとる。ただし，点 \( P \) は
点 \( A，B \) と重ならないものとする。
３ 点 \( B \) を中心として，線分 \( BP \) を半径とする
円 \( B \) をかく。
４ 円 \( O \) と円 \( B \) の交点をそれぞれ \( C，D \) と
する。
５ 点 \( C \) と点 \( D \) を結び，線分 \( AB \) と線分 \( CD \)
の交点を \( E \) とする。
６ 点 \( C \) と３点 \( A，P，B \) をそれぞれ結ぶ。
なお，「点 \( P \) を線分 \( AB \) 上のどこにとっても，線分 \( AB \) と線分 \( CD \) は垂直に交わる。」
このことは，(1)～(4) の解答において証明せずに用いてよい。
(1) 図１において，点 \( P \) を，\( AP=2 \; cm \) の位置にとったとき，\( BC \) の長さを求めなさい。
\( AB=6 \; cm，AP=2 \; cm \) より，\( BP=4 \; cm \) であり，
線分\( BP，BC \) は，円 \( B \) の半径なので，
\( BC=BP=4 \; cm \)
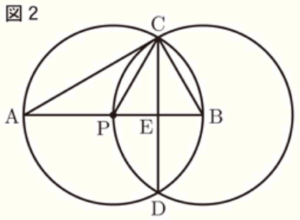
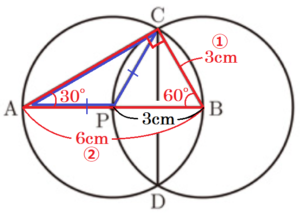
(2) 図２は，図１において，点 \( P \) を円 \( O \) の中心と重なるように動かしたものである。
ただし，円 \( O \) の中心を表す文字 \( O \) を省いて表している。
① \( ∠ACP \) の大きさを求めなさい。
直径 \( AB \) に対する円周角なので，\( ∠ACB=90° \)
点 \( P \) は，円 \( O \) の中心なので，\( BP=3 \; cm \)
円 \( B \) の半径なので，\( BC=BP=3 \; cm \)
条件より，\( AB=6 \; cm \)
よって，\( △ABC \) は，
\( AB：BC=2：1 \) の直角三角形なので，
３つの内角は，\( 30°，60°，90° \) であり，
\( ∠CAP=30° \)
線分 \(AP，CP\) は，円 \( O \) の半径なので，
\( △PAC \) は，二等辺三角形です。
二等辺三角形の底角は等しいので，
\( ∠ACP=∠CAP=30° \)
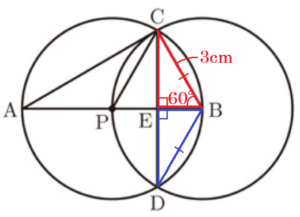
➁ \( CD \) の長さを求めなさい。
線分 \( BP \) は，円 \( O \) の半径なので，\( BP=3 \; cm \)
線分\( BP，BC \) は，円 \( B \) の半径なので，
\( BC=BP=3 \; cm \)
\( △BCE \) は，\( 30°，60°，90° \) の直角三角形になので，
\( CE=\dfrac{\sqrt{3}}{2}BC=\dfrac{3\sqrt{3}}{2} \; (cm) \)
線分 \( BP \) は，円 \( B \) の半径なので，
\( △BCD \) は二等辺三角形であり，
\( BE⊥CD \) なので，\( △BCE≡△BDE \)
よって，
\( CD=2CE=3\sqrt{3} \; (cm) \)
【参考】
\( △BCE \) と \( △BDE \) は
斜辺と他の１辺がそれぞれ等しいので，
\( △BCE≡△BDE \)
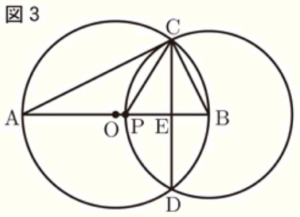
(3) 桜さんは，作図ソフトで何度も点 \( P \) を線分 \( AB \) 上で動かしているうちに，次の２つのことが成り立つのではないかと予想を立てた。
〔予想〕
点 \( P \) を線分 \( AB \) 上のどこにとっても，
１ \( △ABC \) と \( △CBE \) は相似である。
２ 線分 \( CP \) は \( ∠ACE \) を二等分する。
桜さんの予想は，図３を用いて，次のようにそれぞれ証明することができる。
〔予想１の証明〕
\( △ABC \) と \( △CBE \) で，
あ だから，\( ∠ACB=90° \)
\( AB⊥CD \) だから，\( ∠CEB=90° \)
よって， \( ∠ACB=∠CEB \) ･･･ ①
い
〔予想２の証明〕
あ だから，\( ∠ACB=90° \)
\( ∠ACB=∠ACP+∠PCB \) より
\( ∠ACP=90°-∠PCB \) ･･･ ➀
\( AB⊥CD \) だから，\( △CPE \) は
\( ∠CEB=90° \) の直角三角形であり，
\( ∠PCE=90°-∠CPE \) ･･･ ➁
う
よって，\( ∠PCB=∠ \) え ･･･ ➂
➀，➁，➂ より，\( ∠ACP=∠PCE \)
したがって，線分 \( CP \) は \( ∠ACE \) を二等分する。
➀ あ に当てはまる，\( ∠ACB=90° \) の根拠となることがらを書きなさい。ただし，予想１の証明 の あ と 予想２の証明 の あ には共通なことがらが入る。
➁ い に証明の続きを書き，予想１の証明 を完成させなさい。
➂ 予想２の証明 において， う には ➂ の根拠となることがらを， え には最も適切な角を記号を用いて，それぞれ書きなさい。
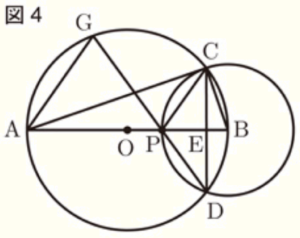
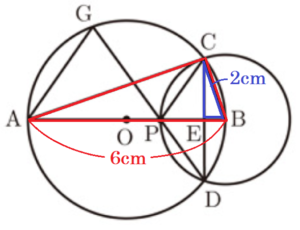
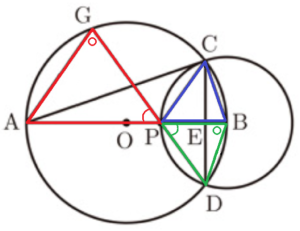
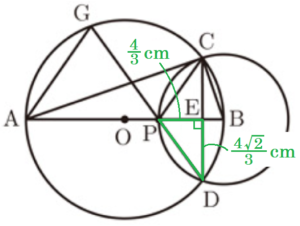
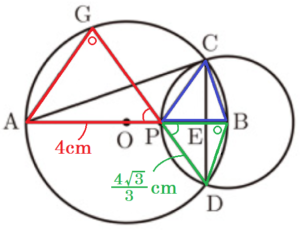
(4) 図４は，点 \( P \) を，\( AP=4 \; cm \) の位置まで動かしたものである。このとき，線分 \( DP \) を延長した直線と円 \( O \) の交点を \( G \) とし，点 \( A \) と点 \( G \) を結ぶ。
➀ \( △CEP \) の面積を求めなさい。
\( △ABC \) ∽ \( △CBE \) なので，
\( AB：CB=BC：BE \)
\( 6：2=2：BE \)
\( BE=\dfrac{2}{3} \; (cm) \)
\( BP=2 \; cm \) なので，
\( PE=BP-BE=\dfrac{4}{3} \; (cm) \)
三平方の定理より，
\( CE^2=BC^2-BE^2 \)
\( =2^2- \left( \dfrac{2}{3} \right)^2 \)
\( =\dfrac{32}{9} \)
\( CE=\dfrac{4\sqrt{2}}{3} \; (cm) \)
\( △CEP=PE \times CE \times \dfrac{1}{2} \)
\( =\dfrac{4}{3} \times \dfrac{4\sqrt{2}}{3} \times \dfrac{1}{2} \)
\( =\dfrac{8\sqrt{2}}{9} \; (cm^2) \)
➁ \( △BCP \) と \( △GAP \) の面積の比を求め，最も簡単な整数の比で表しなさい。
\( △BCP≡△BDP \) であることを利用し，\( △BDP \) と \( △GAP \) の面積比を求めることにします。
\( △BCP≡△BDP \) なので，
\( △BDP \) と \( △GAP \) に注目すると，
円周角が等しいので，\( ∠DBP=∠AGP \) ･･･ ①
対頂角は等しいので，\( ∠DPB=∠APG \) ･･･ ➁
①➁より，２組の角がそれぞれ等しいので，
\( △BDP \) ∽ \( △GAP \)
ここから，\( △BDP \) と \( △GAP \) の相似比がわかれば，面積比を求めることができます。
\( PE=\dfrac{4}{3} \; cm，DE=CE=\dfrac{4\sqrt{2}}{3} \; cm \) なので，
三平方の定理より，
\( DP^2=PE^2+DE^2 \)
\( =\left( \dfrac{4}{3} \right)^2+ \left( \dfrac{4\sqrt{2}}{3} \right)^2 \)
\( =\dfrac{16}{9}+\dfrac{32}{9} \)
\( =\dfrac{16}{3} \)
\( DP=\dfrac{4\sqrt{3}}{3} \; (cm) \)
\( △BDP \) ∽ \( △GAP \)，\( DP=\dfrac{4\sqrt{3}}{3} \; cm，AP=4 \; cm \) より，
相似比は，
\( DP：AP=\dfrac{4\sqrt{3}}{3}：4=1：\sqrt{3} \)
相似な三角形の面積比は，相似比の２乗の比になるので，
\( △BDP：△GAP=1^2：\sqrt{3}^2=1：3 \)
よって，\( △BCP≡△BDP \) より，
\( △BCP：△GAP=1：3 \)
