大問1
(1) \( 3-2 \times \left(-\dfrac{1}{2} \right) \) を計算せよ。
(2) \( \sqrt{48}+\dfrac{3}{\sqrt{3}} \) を計算せよ。
【解説】
\( =4\sqrt{3}+\sqrt{3} \)
\( =5\sqrt{3} \)
(3) 家から学校までの通学路の距離は \( 5 \; km \) ある。通学路の途中に本屋があり,家から本屋まで時速 \( 3 \; km \) で歩くと \( a \) 時間かかる。このとき,本屋から学校までの距離を \( a \) を用いて表せ。
【解説】
家から本屋まで時速 \( 3 \; km \) で \( a \) 時間歩くと,\( 3a \; km \) 歩くことができるので,
残りの本屋から学校までの距離は,\( 5-3a \; km \) と表すことができます。
(4) 連立方程式 \( \left\{ \begin{array}{}
2x-y=5 \\
3x+2y=-3 \\
\end{array} \right. \) を解け。
【解説】
\( \left\{ \begin{array}{}
2x-y=5 \;\; ・・・ \;\; ➀ \\
3x+2y=-3 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 2+ \) ➁
\( 7x=7 \)
\( x=1 \)
➀に代入すると,
\( 2 \times 1-y=5 \)
\( y=-3 \)
(5) 2次方程式 \( x^2-3x-4=0 \) を解け。
【解説】
\( (x+1)(x-4)=0 \)
\( x=-1,4 \)
(6) ある高校の1クラスの生徒 \( 40 \) 人で,当たりくじつきのアイスを \( 1 \) 人 \( 1 \) 本ずつ食べたところ,その中の \( 2 \) 本が当たりだった。全校生徒 \( 600 \) 人で,このアイスを \( 1 \) 人 \( 1 \) 本ずつ食べたとき,およそ何本が当たりであると考えられるか。
【解説】
「1クラスの生徒数」:「クラスの中のあたりの数」 \( = \) 「全校生徒の数」:「全校でのあたりの数」
となるので,「全校でのあたりの数」を \( P \) とすると,
\( 40:2=600:P \)
\( 40P=1200 \)
\( P=30 \)(本)
(7) \( 2024=\dfrac{22 \times 23 \times 24}{□} \) と表せる。□に入る自然数を答えよ。
【解説】
\( 2024 \) を素因数分解すると,\( 2024=2^3 \times 11 \times 23 \) なので,
\( 2024=(2 \times 11) \times 23 \times 2^2=22 \times 23 \times 4 \)
と表すことができます。
問題の式は,
\( 2024=22 \times 23 \times \dfrac{24}{□} \)
と表すこともできるので,
\( 22 \times 23 \times 4=22 \times 23 \times \dfrac{24}{□} \)
\( 4=\dfrac{24}{□} \)
\( □=6 \)
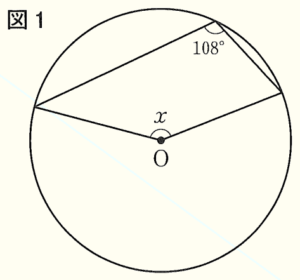
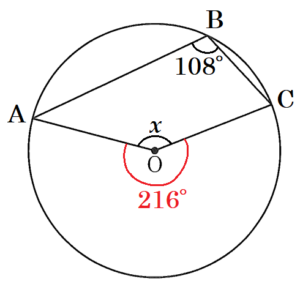
(8) 図1のような円 \( O \) において,\( ∠x \) の大きさを求めよ。
【解説】
右の図のように点 \( A,B,C \) とすると,\( ∠ABC \) は弧 \( AC \) の円周角,\( ∠AOC \) (\( ∠x \) の反対側) は弧 \( AC \) の中心角なので,
\( ∠AOC=2 \times 108°=216° \)
よって,
\( ∠x=360°-216°=144° \)
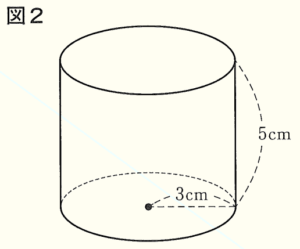
(9) 図2のような,底面の円の半径が \( 3 \; cm \),高さが \( 5 \; cm \) の円柱の体積は何 \( cm^3 \) か。
【解答】
\( 45 \pi{} \; cm^3 \)
【解説】
\( \pi{} \times 3^2 \times 5=45 \pi{} \; (cm^3) \)
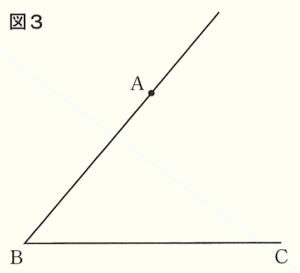
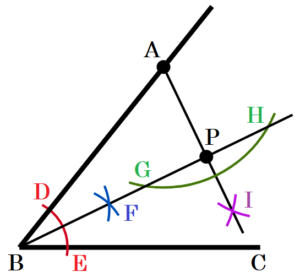
(10) 図3において,\( ∠ABC \) の二等分線上にあって,点 \( A \) からの距離が最も短い点 \( P \) を定規とコンパスを用いて解答用紙の図3に作図して求め,その位置を点 \( \bullet \) で示せ。
ただし,作図に用いた線は消さずに残しておくこと。
【解答】
手順1 点 \( B \) を中心に円弧を描く。
(直線 \( AB,BC \) との交点を,
それぞれ点 \( D,E \) とします。)
手順2 2点 \( D,E \) を中心に円弧を描く。
(交点を点 \( F \) とします。)
手順3 2点 \( B,F \) を通る直線を描く。
手順4 点 \( A \) を中心に円弧を描く。
(直線 \( BF \) との交点を,
それぞれ点 \( G,H \) とします。)
手順5 2点 \( G,H \) を中心に円弧を描く。
(交点を点 \( I \) とします。)
手順6 2点 \( A,I \) を通る直線を描く。
手順3と手順6の直線の交点が求める点になります。
【解説】
\( ∠ABC \) の二等分線上にあって,点 \( A \) からの距離が最も短くなるのは,
点 \( A \) から\( ∠ABC \) の二等分線に対して垂線をひいたときになります。
大問2
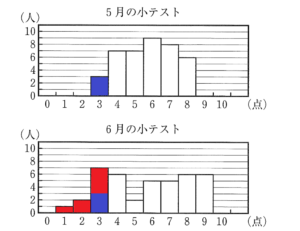
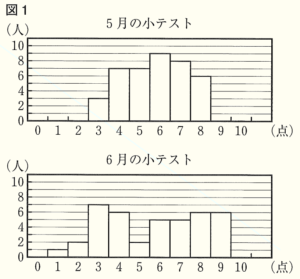
問1 図1は,ある中学校の1年生40人に対して,5月と6月に行った数学の10点満点の小テストの得点の結果をもとにそれぞれ作成したヒストグラムである。このとき,次の(1)~(3)に答えよ。
(1) 5月の小テストで,得点が4点以下の生徒は何人か。
【解説】
ヒストグラムより,3点の人は3人,4点の人は7人(0~2点の人はいない)
なので,合計で10人
(2) 5月の小テストの得点と6月の小テストの得点の散らばりの程度(散らばりのぐあい)はどちらが大きいか,5月の小テストのヒストグラムと6月の小テストのヒストグラムから読み取れる数値を比較して説明せよ。
【解答】
5月の小テストの得点の範囲は5点,6月の小テストの得点の範囲は8点なので,
散らばりの程度は,6月の小テストの得点の方が大きい。
(3) 次の①~④について,図1から読み取れることとして,必ず正しいと判断できるものを1つ選び,その番号を書け。
➀ 最頻値(モード) は,5月の小テストよりも6月の小テストの方が大きい。
➁ 中央値 (メジアン)は,5月の小テストよりも6月の小テストの方が大きい。
➂ 5月の小テストの得点が7点以上の生徒のうち,6人が6月の小テストで得点を伸ばした。
④ 5月の小テストの得点よりも6月の小テストの得点が低い生徒が7人以上いる。
【解説】
➀ 5月の小テストの最頻値は6点,6月の小テストの最頻値は3点なので,
最頻値は5月の小テストの方が大きい。
➁ 全体で40人なので,中央値は,得点の低い方から20番目と21番目の生徒の平均値になります。
5月の小テスト ・・・ 5点以下の階級の度数は \( 3+7+7=17 \)(人),
6点の階級の度数は \( 9 \) 人なので,
20番目の人と21番目の生徒の得点はどちらも6点であり,平均値も6点。
6月の小テスト ・・・ 5点以下の階級の度数は \( 1+2+7+6+2=18 \)(人),
6点の階級の度数は \( 5 \) 人なので,
20番目の人と21番目の生徒の得点はどちらも6点であり,平均値も6点。
つまり,5月の小テストも6月の小テストも中央値は6点になります。
➂ ヒストグラムのデータを比較するだけでは,誰が何点取ったかは判断できません。
➃ 5月の小テストでは得点が2点以下の生徒はいないので,6月の小テストで2点以下であった3人は,
確実に6月の小テストの方が得点が低かったといえます。
また,得点が3点の生徒は,5月の小テストでは3人,6月の小テストでは7人いるので,
5月の小テストで得点が3点だった3人が6月の小テストでも3点だったと仮定しても,
残りの4人は得点が下がった人になります。
よって,「5月の小テストの得点よりも6月の小テストの得点が低い生徒が7人以上いる」。
問2 図2のように,箱の中に \( 1 \) から \( 6 \) までの数字が1つずつ書かれたカードが6枚入っており,この箱の中からカードを取り出す。このとき,次の(1),(2)に答えよ。ただし,どのカードが取り出されることも同様に確からしいとする。
(1) カードを1枚取り出し,取り出したカードに書かれた数字を確認してもとに戻す操作を行う。次の①~④について,正しいものを1つ選び,その番号を書け。
① この操作を5回行い,\( 1 \) の数字が書かれたカードを1回も取り出さなかったとき,もう1回
この操作を行うと,必ず \( 1 \) の数字が書かれたカードを取り出す。
➁ この操作を60回行う。50回目までに \( 1 \) の数字が書かれたカードを1回も取り出さなかった
とき,その後の10回の操作では,\( 1 \) の数字が書かれたカードを取り出しやすくなる。
➂ この操作を6000回行うと,\( 1 \) の数字が書かれたカードを取り出す回数はおよそ1000回
である。
④ この操作の回数にかかわらず,\( 1 \) の数字が書かれたカードを取り出した回数を操作した回数
で割ると,つねに \( \dfrac{1}{6} \) になる。
【解説】
➀ どのカードが取り出されることも同様に確からしいので,
1回ごとの「\( 1 \) の数字が書かれたカードを取り出す確率」は,つねに \( \dfrac{1}{6} \) になります。
また,取り出したカードはもとに戻すので,どのカードを取り出しても,次のカードの取り出し方
には関係がありません。
よって,「必ず \( 1 \) の数字が書かれたカードを取り出す」ことにはなりません。
➁ ➀の場合と同様で,50回目までの結果がどのような結果であったとしても,残り10回のカードの
取り出し方には関係がありません。
➂ 例えば,2回目までの結果を考えると,2回とも \( 1 \) の数字が書かれたカードを取り出すことも
ありますが,これを数百回,数千回と回数を増やしていくと,得られる結果は,計算上求められる
確率に近づいていきます。
1回ごとの「\( 1 \) の数字が書かれたカードを取り出す確率」は \( \dfrac{1}{6} \) なので,
6000回行った場合,\( 1 \) の数字が書かれたカードを取り出す回数は,
およそ \( 6000 \times \dfrac{1}{6}=1000 \)(回)になります。
➃ 2回目までの結果で,2回とも \( 1 \) の数字が書かれたカードを取り出した場合を考えると,
取り出した回数を操作した回数で割ると,\( \dfrac{2}{2}=1 \) となり,\( \dfrac{1}{6} \) になるとは限りません。
(2) カードを同時に2枚取り出す操作を1回行うとき,次の文中の ア , イ に適当な数を入れ、文を完成させよ。
「取り出した2枚のカードに書かれた数の和が3となる確率は ア であり,取り出した2枚のカードに書かれた数の和が イ となる確率は \( \dfrac{1}{5} \) である。」
【解答】
ア ・・・ \( \dfrac{1}{15} \)
イ ・・・ \( 7 \)
【解説】
2枚のカードの取り出し方とそれぞれの場合のカードに書かれた数の和を樹形図として書き出すと,
すべての場合の数は15通りになっています。
(同時に取り出していることに注意!)
ア ・・・ 和が3になるのは1通りなので,求める確率は \( \dfrac{1}{15} \)
イ ・・・ 和が イ となる場合の数を \( x \) 通りとすると,確率が \( \dfrac{1}{5} \) になるのは,
\( \dfrac{x}{15}=\dfrac{1}{5} \)
\( x=3 \)(通り)
のときなので,樹形図から,3通りの選び方があるのは和が7のときになります。

【解答】
3つの数の中で一番小さい数を \( n \) とすると,
残りの2つの数は \( n+7,n+8 \) と表すことができる。
このとき,3つの数の和は
\( n+(n+7)+(n+8)=3n+15 \)
\( =3(n+5) \)
\( n \) は自然数であることから,\( n+5 \) も自然数であり,
\( 3(n+5) \) は3の倍数である。
よって,3つの数の和は \( 3 \) の倍数となる。
大問3
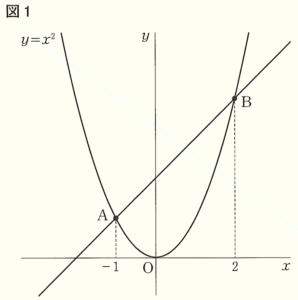
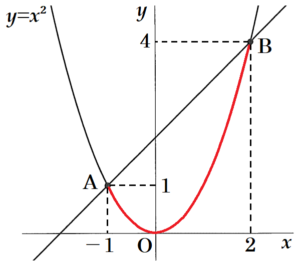
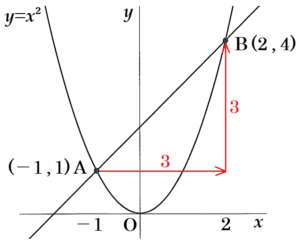
図1,図2のように,関数 \( y=x^2 \) のグラフ上に2点 \( A,B \) があり,\( A,B \) の \( x \) 座標はそれぞれ \( -1,2 \) である。原点を \( O \) として,次の問いに答えなさい。
問1 点 \( B \) の \( y \) 座標を求めよ。
【解説】
点 \( B \) は,\( y=x^2 \) 上の点で,
\( x \) 座標が \( 2 \) なので,\( y \) 座標の値は,
\( y=2^2=4 \)
問2 関数 \( y=x^2 \) について,\( x \) の変域が \( -1≦x≦2 \) のときの \( y \) の変域を求めよ。
【解説】
右の図の赤い部分の曲線において,
最小値になるのは,\( x=0 \) のときで,\( y=0 \)
最大値になるのは,\( x=2 \) のときで,\( y=4 \)
よって,\( y \) の変域は,\( 0≦y≦4 \)
問3 直線 \( AB \) の式を求めよ。
【解説】
\( A(-1,1),B(2,4) \) を通るので,
直線 \( AB \) の式を \( y=ax+b \) とすると,
傾き \( a=\dfrac{4-1}{2-(-1)}=1 \)
\( y=x+b \) に \( x=2,y=4 \) を代入すると,
\( 4=2+b \)
\( b=2 \)
よって,求める式は \( y=x+2 \)
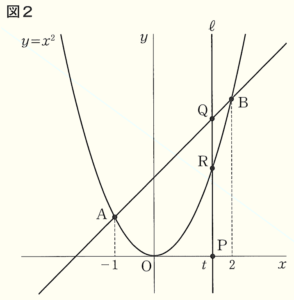
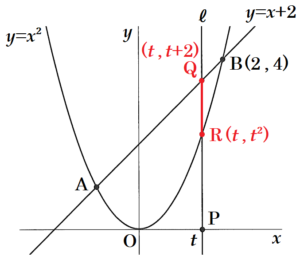
問4 図2のように,\( x \) 軸上に点 \( P(t, 0) \) をとる。点 \( P \) を通り,\( y \) 軸に平行な直線を \( ℓ \) とし,直線 \( ℓ \) と直線 \( AB \) の交点を \( Q \),直線 \( ℓ \) と \( y=x^2 \) のグラフの交点を \( R \) とする。このとき、次の(1),(2)に答えよ。ただし,\( 0<t<2 \) とする。
(1) 線分 \( QR \) の長さを \( t \) を用いて表せ。
【解説】
点 \( Q \) は,\( y=x+2 \) 上の点で,
\( x \) 座標が \( t \) なので,
\( y \) 座標の値は,\( y=t+2 \)
点 \( R \) は,\( y=x^2 \) 上の点で,
\( x \) 座標が \( t \) なので,
\( y \) 座標の値は,\( y=t^2 \)
右の図のとおり,\( 0<x<2 \) の範囲において,
点 \( Q \) の \( y \) 座標の値は
点 \( R \) の \( y \) 座標の値よりも大きいので,
線分 \( QR \) の長さは,
\( QR=t+2-t^2=-t^2+t+2 \)
(2) 線分 \( PR \) の長さが線分 \( QR \) の長さの2倍となるとき,\( t \) の値を求めよ。
【解答】
\( t=\dfrac{1+\sqrt{13}}{3} \)
【解説】
線分 \( PR \) の長さは \( t^2 \) なので,
\( t^2=2(-t^2+t+2) \)
\( t^2=-2t^2+2t+4 \)
\( 3t^2-2t-4=0 \)
\( t=\dfrac{-(-2)±\sqrt{(-2)^2-4 \times 3 \times (-4)}}{2 \times 3} \)
\( =\dfrac{2±\sqrt{4+48}}{6} \)
\( =\dfrac{1±\sqrt{13}}{3} \)
\( 0<t<2 \) より,あてはまるのは \( t=\dfrac{1+\sqrt{13}}{3} \)
大問4
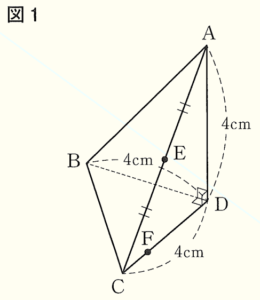
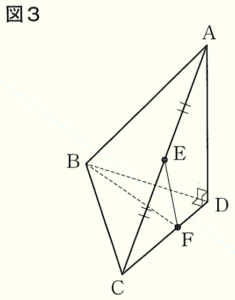
図1~図3のように,\( AD=BD=CD=4 \; cm,∠ADB=∠ADC=∠BDC=90° \) である三角錐 \( ABCD \) がある。辺 \( AC \) の中点を \( E \) とし,辺 \( CD \) 上を動く点を \( F \) とする。このとき,次の問いに答えなさい。
問1 辺 \( AC \) の長さは何 \( cm \) か。
【解答】
\( AC=4\sqrt{2} \; cm \)
【解説】
\( △ACD \) は,辺 \( AC \) が斜辺の直角二等辺三角形なので,
\( AC=\sqrt{2}CD=4\sqrt{2} \; (cm) \)
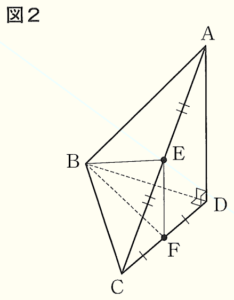
問2 図2のように,点 \( F \) が辺 \( CD \) の中点となるとき,次の(1),(2)に答えよ。
(1) \( △BCF \) の面積は何 \( cm^2 \) か。
【解説】
\( △BCF \) は,底辺 \( CF=2 \; cm \),高さ \( BD=4 \; cm \) の三角形
と考えることができるので,
\( △BCF=2 \times 4 \times \dfrac{1}{2}=4 \; (cm^2) \)
(2) 三角錐 \( EBCF \) の体積は何 \( cm^3 \) か。
【解答】
\( \dfrac{8}{3} \; cm^3 \)
【解説】
\( △ACD \) において,中点連結定理より,
\( EF=\dfrac{1}{2}AD=2 \; cm \)
なので,
三角錐 \( EBCF \) の体積を \( V \) とすると,
\( V=4 \times 2 \times \dfrac{1}{3}=\dfrac{8}{3} \; (cm^3) \)
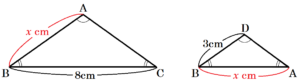
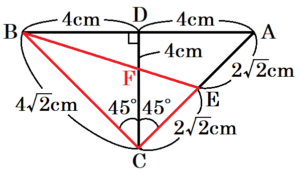
問3 図3において,2つの線分 \( BF,FE \) の長さの和 \( BF+FE \) が最小となるとき,\( BF+FE \) の長さは何 \( cm \) か。
【解答】
\( 2\sqrt{10} \; cm \)
【解説】
\( BF+FE \) が最小となるとき,3点 \( B,F,E \) は一直線上に並びます。
\( △BCD \) は,辺 \( BC \) が斜辺の直角二等辺三角形なので,
\( BC=\sqrt{2}CD=4\sqrt{2} \; (cm) \)
面 \( BCD \) と面 \( ACD \) を展開すると,
\( △BCD \) と \( △ACD \) は直角二等辺三角形なので,
\( ∠BCD=∠ACD=45° \) であり,\( ∠ACB=90° \)
点 \( E \) は,辺 \( AC \) の中点なので,
\( CE=\dfrac{1}{2}AC=2\sqrt{2} \; (cm) \)
\( △BCE \) において,三平方の定理より,
\( BE^2=(4\sqrt{2})^2+(2\sqrt{2})^2=40 \)
\( BE=2\sqrt{10} \; (cm) \)
大問5
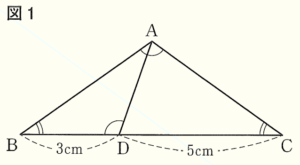
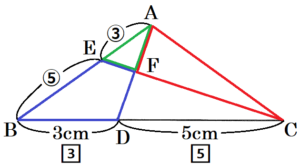
図1~図3のように,\( ∠ABC=∠ACB \) である鈍角三角形 \( ABC \) がある。辺 \( BC \) 上に \( ∠BAC=∠ADB \) となる点 \( D \) をとると,\( △ABC \) ∽ \( △DBA \) となる。\( BD=3 \; cm,CD=5 \; cm \) とするとき,次の問いに答えなさい。
問1 線分 \( AD \) の長さは何 \( cm \) か。
【解説】
\( △ABC \) は,\( ∠ABC=∠ACB \) より,\( AB=AC \) の二等辺三角形になっています。
次に,\( △ABC \) ∽ \( △DBA \) より,\( △DBA \) は \( AD=BD \) の二等辺三角形になっています。
よって,\( AD=BD=3 \; cm \)
問2 辺 \( AB \) の長さは何 \( cm \) か。
【解答】
\( 2\sqrt{6} \; cm \)
【解説】
\( AB=x \; cm \) とすると,\( △ABC \) ∽ \( △DBA \) より,
\( AB:DB=BC:BA \)
\( x:3=8:x \)
\( x^2=24 \)
\( x=2\sqrt{6} \; (cm) \) ( \( x>0 \) より)
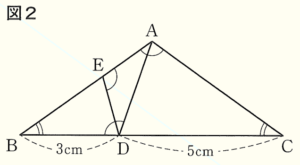
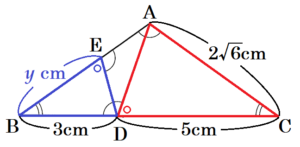
問3 図2のように,辺 \( AB \) 上に \( ∠ADB=∠DEA \) となる点 \( E \) をとる。このとき,次の(1)~(3)に答えよ。
(1) \( △CAD \) ∽ \( △BDE \) であることを次のように証明した。 ア ~ ウ にあてはまる内容を書き入れて,証明を完成させよ。ただし,同じ記号には同じ内容が入る。
(証明)
\( △CAD \) と \( △BDE \) において
仮定より \( ∠ABC=∠ACB \) であるので,\( ∠DCA=∠EBD \) ・・・ ①
仮定より \( ∠ADB=∠DEA \) ・・・ ②
また \( ∠CDA= \) ア ° \( -∠ADB \) ・・・ ③
また \( ∠ \) イ \( = \) ア ° \( -∠DEA \) ・・・ ④
➁,③,④より,\( ∠CDA=∠ \) イ ・・・ ⑤
①,⑤より, ウ がそれぞれ等しいから
\( △CAD \) ∽ \( △BDE \)
【解答】
ア ・・・ \( 180 \)
イ ・・・ \( BED \)
ウ ・・・ 2組の角
(2) 線分 \( AE \) の長さと線分 \( EB \) の長さの比を最も簡単な整数の比で表せ。
【解説】
\( EB=y \; cm \) とすると,
\( △CAD \) ∽ \( △BDE \) より,
\( AC:DB=DC:EB \)
\( 2\sqrt{6}:3=5:y \)
\( 2\sqrt{6}y=15 \)
\( y=\dfrac{5\sqrt{6}}{4} \; (cm) \)
\( AB=2\sqrt{6} \; cm \) より,
\( AE=2\sqrt{6}-\dfrac{5\sqrt{6}}{4}=\dfrac{3\sqrt{6}}{4} \; (cm) \)
よって,
\( AE:EB=\dfrac{3\sqrt{6}}{4}:\dfrac{5\sqrt{6}}{4}=3:5 \)
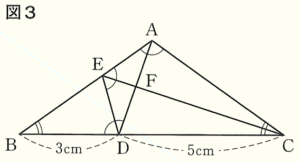
(3) 図3のように,線分 \( CE \) と線分 \( AD \) の交点を \( F \) とする。\( △ACF \) の面積と四角形 \( BDFE \) の面積の比を最も簡単な整数の比で表せ。
【解答】
\( △ACF: \) 四角形 \( BDFE=1:1 \)
【解説】
四角形 \( BDFE \) が面積を求めにくい形であることに注目すると,
四角形 \( BDFE \) は,\( △ABD \) から \( △AEF \) を取り除いたものです。
同様に,\( △ACF \) は,\( △ACE \) から \( △AEF \) を取り除いたものです。
ここから,\( △ABD \) と \( △ACE \) の面積が,\( △ABC \) の何倍であるかを最初に求めていきます。
(2)より,\( AE:EB=3:5 \) なので,
\( AE:AB=3:8 \)
\( △ACE \) と \( △ABC \) は,高さが共通なので,
\( △ACE:△ABC=AE:AB=3:8 \)
であり,
\( △ACE=\dfrac{3}{8}△ABC \) ・・・ ➀
\( BD:DC=3:5 \) なので,\( BD:BC=3:8 \)
\( △ABD \) と \( △ABC \) は,高さが共通なので,
\( △ABD:△ABC=BD:BC=3:8 \)
であり,
\( △ABD=\dfrac{3}{8}△ABC \) ・・・ ➁
➀➁より,\( △ACE=△ABD \)
\( △ACF=△ACE-△AEF \)
四角形 \( BDFE=△ABD-△AEF \)
\( △ACE=△ABD \)
より,
\( △ACF= \) 四角形 \( BDFE \) なので,
\( △ACF: \) 四角形 \( BDFE=1:1 \)
大問6
学さんと学さんのお姉さんは,車のナンバープレートを見て数遊びをしている。2人の会話を読んで,あとの問いに答えなさい。
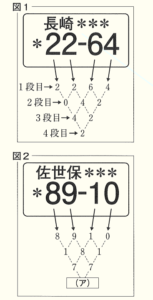
姉:4つの数が表示されているナンバープレートだけに注目してみよ
う。図1のように、ナンバープレートに表示されている4つの数
を左から順に書き並べて,それを1段目とするね。次に,1段目の
隣り合う数の差を2段目に書くことにするよ。ただし,差は \( 0 \)
以上とするね。これを続けると,4段目の数はどんな数になるか
な。例えば、ナンバープレートの表示が \( 22-64 \) だと,4つの
数 \( 2,2,6,4 \) を1段目に並べ,\( 2 \) と \( 2 \) の差が \( 0 \),\( 2 \) と \( 6 \) の
差が \( 4 \),\( 6 \) と \( 4 \) の差が \( 2 \) だから,2段目は \( 0,4,2 \) が並ぶ
よ。これを続けると,4段目の数は \( 2 \) となるね。図2のように,
ナンバープレートの表示が \( 89-10 \) だと,4段目の数は (ア)
となるよ。
学:なるほど。\( 22-64 \) を \( 2264 \) というように,ナンバープレート
の4つの数を \( 1000 \) 以上 \( 9999 \) 以下の自然数と考えて,1段目
にその自然数の各位の数を左から順に書き並べて,4段目の数を
調べるということだね。
姉:そうだね。では,最初にすべての4けたの自然数について,4段
目の数を調べたら,4段目の数は, \( 2 \) や ア を含めて
何通りあるかな。
学:うん。調べてみるね。
(数分後)
学:すべての場合を調べなくても,\( 1000 \) や \( 2000 \) などの自然数を
いくつか調べれば,4段目の数は イ 通りあることが分かる
よ。
姉:そうだね。それでは,\( 5012 \) や \( 3486 \) といった各位の数が異なる
4けたの自然数の場合も,4段目の数は イ 通りあるかな。
学: 少し考えさせて。
(数分後)
学:4段目の数は ウ にはならないので, イ 通りはないね。
姉:よくわかったね。それでは,最後に \( 1234 \) や \( 2310 \) や \( 5746 \)
といった連続する4つの整数を並べかえてできる4けたの自然数
で,4段目の数が奇数になるものがあるか考えてみよう。私が今
まで調べた中では,見つけられなかったんだよね。でも,すべて
の場合を調べたわけではないから,4段目の数が奇数になるもの
がないとは言い切れないんだけど,どのように考えたらいいかな。
学:わかった。考えてみるね。
(数分後)
学:4段目から考えたらどうかな。4段目の数が奇数となるためには,
3段目の2つの数は,偶数と奇数でなければならないね。偶数と
偶数,奇数と奇数では,差は偶数となり,奇数にならないからね。
姉:なるほど。そうやって次は2段目,1段目と考えていけば,
【連続する4つの整数を並べかえてできる4けたの自然数で,
4段目の数が奇数になるものはない】ことが説明できそうだね。
問1 ア ~ ウ にあてはまる数を答えよ。ただし,同じ記号には同じ数が入る。
【解答】
ア ・・・ \( 0 \)
イ ・・・ \( 10 \)
ウ ・・・ \( 9 \)
【解説】
ウ ・・・ 4段目をスタートとして,4段目の数が \( 9 \) になるように,この図を作ってみます。
4段目の数が \( 9 \) であるとき,3段目の2つの数は必ず \( 9 \) と \( 0 \) になります。
また,3段目の \( 9 \) の上(2段目)の2つの数も必ず \( 9 \) と \( 0 \) になります。
このとき,2段目ののこり1つの数は,\( 9 \) または \( 0 \) になります。
1段目についても同様に考え,この図を完成させると,4つの数が \( 9 \) または \( 0 \) になります。
よって,「各位の数が異なる」という条件にあてはまらないので,
4段目の数が \( 9 \) になることはありません。
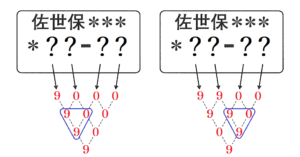 注)この図は,組み合わせの一部です。
注)この図は,組み合わせの一部です。
問2 下線部で示した内容が正しいことを説明せよ。ただし,説明は解答用紙の「奇数を○,偶数を×とすると,4段目が○ (奇数)となるためには,3段目は、○×か,×○でなければならない。」 に続けて完成させよ。
【解答】
奇数を○,偶数を×とすると,4段目が○ (奇数)となるためには,3段目は、○×か,×○でなければならない。
このとき,2段目の組み合わせは,
○××,×○○,××○,○○×
のいずれかになる。
さらに,1段目の組み合わせは,
○×××,×○○○,○○×○,××○×,×××○,○○○×,○×○○,×○××
のいずれかになる。
これらは,「偶数1個,奇数3個」または「偶数3個,奇数1個」の組み合わせになっている。
連続する4つの整数を並べ替えるとき,偶数,奇数それぞれ2個ずつなければならないので,条件に合っていない。
よって,連続する4つの整数を並べかえてできる4けたの自然数で,4段目の数が奇数になるものはない。
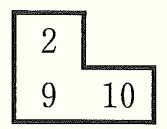 や
や 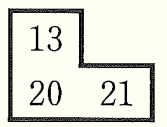 のように,
のように, で囲まれた3つの数について「3つの数の和は \( 3 \) の倍数となる」ことを文字 \( n \) を使って証明せよ。ただし,証明は解答用紙の「3つの数の中で一番小さい数を \( n \) とすると,」に続けて完成させよ。
で囲まれた3つの数について「3つの数の和は \( 3 \) の倍数となる」ことを文字 \( n \) を使って証明せよ。ただし,証明は解答用紙の「3つの数の中で一番小さい数を \( n \) とすると,」に続けて完成させよ。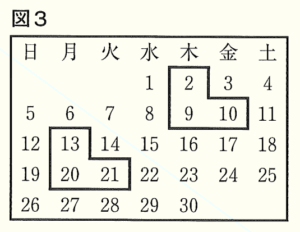


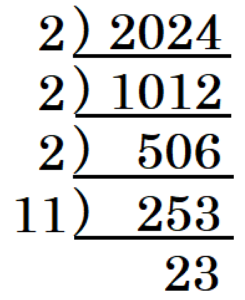



 注)この図は,組み合わせの一部です。
注)この図は,組み合わせの一部です。
