大問1
(1) 次の➀~➄の計算をしなさい。
➀ \( 3-7 \)
➁ \( -4^2 \div 8 \)
【解説】
\( =-16 \div 8 \)
\( =-2 \)
➂ \( 4x-7-(4+x) \)
【解説】
\( =4x-7-4-x \)
\( =3x-11 \)
➃ \( \dfrac{3}{8}x^2y^3 \div \dfrac{3}{2}xy \)
【解答】
\( \dfrac{1}{4}xy^2 \)
【解説】
\( =\dfrac{3}{8}x^2y^3 \times \dfrac{2}{3xy} \)
\( =\dfrac{3x^2y^3 \times 2}{8 \times 3xy} \)
\( =\dfrac{1}{4}xy^2 \)
➄ \( 2\sqrt{3}+\sqrt{2} \times \dfrac{6}{\sqrt{6}} \)
【解説】
\( =2\sqrt{3}+\sqrt{2} \times \dfrac{6 \times \sqrt{6}}{\sqrt{6} \times \sqrt{6}} \)
\( =2\sqrt{3}+\sqrt{2} \times \sqrt{6} \)
\( =2\sqrt{3}+\sqrt{12} \)
\( =2\sqrt{3}+2\sqrt{3} \)
\( =4\sqrt{3} \)
(2) 2次方程式 \( 3x^2-5x+1=0 \) を解きなさい。
【解答】
\( x=\dfrac{5±\sqrt{13}}{6} \)
【解説】
この方程式を \( ax^2+bx+c=0 \) と考えると,\( a=3,b=-5,c=1 \) なので,
解の公式より,
\( x=\dfrac{-(-5)±\sqrt{(-5)^2-4 \times 3 \times 1}}{2 \times 3} \)
\( =\dfrac{5±\sqrt{13}}{6} \)
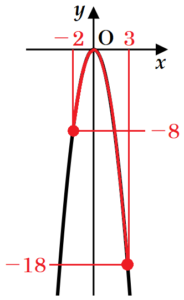
(3) 関数 \( y=-2x^2 \) について,\( x \) の変域が \( -2≦x≦3 \) のときの \( y \) の変域を求めなさい。
【解説】
\( y=ax^2 \; (a<0) \) のグラフにおいて,\( x \) の変域が \( 0 \) を含むとき,\( y \) の最大値は必ず \( 0 \) になります。
また,\( x \) の絶対値が最大になるとき,\( y \) の値は最小値をとります。
\( -2≦x≦3 \) の範囲において,絶対値が最も大きくなるのは \( x=3 \) のときなので,そのときの \( y \) の値は,
\( y=-2 \times 3^2=-18 \)
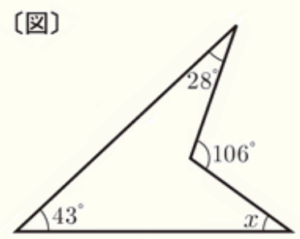
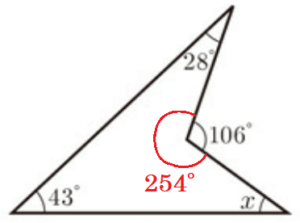
(4) 右の〔 図 〕において,\( ∠x \) の大きさを求めなさい。
【解説】
四角形の内部の残りの1つの角は,
\( 360°-106°=254° \)
であり,四角形の内角の和は \( 360° \) なので,
\( ∠x=360°-(43°+28°+254°)=35° \)
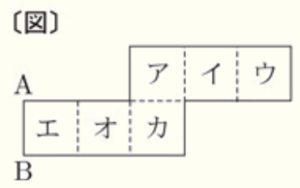
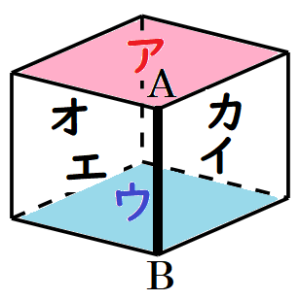
(5) 右の〔 図 〕のような立方体の展開図がある。
この展開図を組み立ててできる立方体において,辺 \( AB \) と垂直になる面を,ア~カからすべて選び,記号を書きなさい。
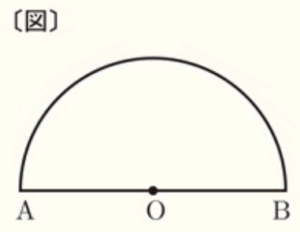
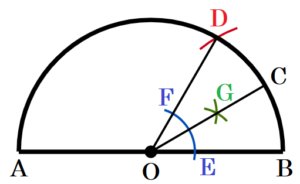
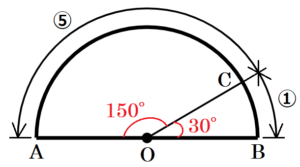
(6) 右の〔 図 〕のように,点 \( O \) を中心として,線分 \( AB \) を直径とする半円がある。
この半円の \( \stackrel{\huge\frown}{ AB } \) 上に, \( \stackrel{\huge\frown}{ AC }:\stackrel{\huge\frown}{ CB }=5:1 \) となるような点 \( C \) を,作図によって求めなさい。
ただし, 作図には定規とコンパスを用い,作図に使った線は消さないこと。
【解答】
手順1 点 \( B \) を中心に線分 \( OB \) を半径とする円弧を描く。
( \( \stackrel{\huge\frown}{ AB } \) との交点を \( D \) とします。)
手順2 2点 \( OD \) を通る直線を描く。
手順3 点 \( O \) を中心に円弧を描く。
( 線分 \( OB,OD \) との交点を \( E,F \) とします。)
手順4 2点 \( E,F \) を中心に円弧を描く。
( 交点を \( G \) とします。)
手順5 2点 \( OG \) を通る直線を描く。
手順5の直線と \( \stackrel{\huge\frown}{ AB } \) の交点が求める点 \( C \) になります。
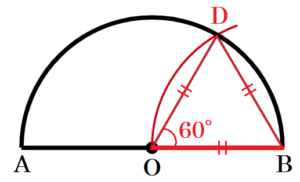
【解説】
中心角の大きさは,円弧の長さに比例します。
\( \stackrel{\huge\frown}{ AC }:\stackrel{\huge\frown}{ CB }=5:1 \) のとき,
\( ∠AOC:∠COB=5:1 \) になるので,
\( ∠COB=180° \times \dfrac{1}{6}=30° \) になります。
\( 30° \) は \( 60° \) の半分であることに注目すると,
\( ∠BOD=60° \) となるような線分 \( OD \) を描くことができれば,
\( ∠BOD \) の二等分線を描くことにより,点 \( C \) を求めることができます。
\( \stackrel{\huge\frown}{ AB } \) 上に \( ∠BOD=60° \) となるような
点 \( D \) をとるとき,
\( OB=OD \) より,\( △OBD \) は正三角形になります。
正三角形において,\( OB=BD \) でもあるので,
点 \( B \) を中心に線分 \( OB \) を半径とする円弧を描くことで,点 \( D \) の場所を求めることができます
大問2
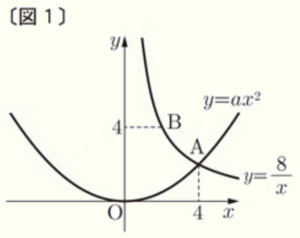
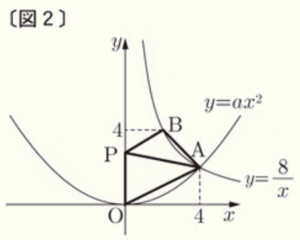
右の〔図1〕のように2つの関数 \( y=ax^2 \) と \( y=\dfrac{8}{x} \; (x>0) \) のグラフが,点 \( A \) で交わっており,点 \( A \) の \( x \) 座標は \( 4 \) である。また,関数 \( y=\dfrac{8}{x} \; (x>0) \) のグラフ上に点 \( B \) があり,点 \( B \) の \( y \) 座標は \( 4 \) である。
次の(1)~(3)の問いに答えなさい。
(1) \( a \) の値を求めなさい。
【解答】
\( a=\dfrac{1}{8} \)
【解説】
点 \( A \) は,\( y=\dfrac{8}{x} \; (x>0) \) 上の点で,\( x \) 座標が \( 4 \) なので,
\( y \) 座標は \( y=\dfrac{8}{4}=2 \)
\( y=ax^2 \) も \( A(4,2) \) を通るので,
\( 2=a \times 4^2 \)
\( 16a=2 \)
\( a=\dfrac{1}{8} \)
(2) 直線 \( AB \) の式を求めなさい。
【解説】
点 \( B \) は,\( y=\dfrac{8}{x} \; (x>0) \) 上の点で,\( y \) 座標が \( 4 \) なので,
\( x \) 座標は
\( 4=\dfrac{8}{x} \)
\( x=\dfrac{8}{4} \)
\( =2 \)
直線 \( AB \) は \( A(4,2),B(2,4) \) を通るので,
傾き \( =\dfrac{2-4}{4-2}=-1 \)
直線 \( AB \) の式を \( y=-x+b \) とすると,
\( A(4,2) \) を通るので,
\( 2=-4+b \)
\( b=6 \)
よって,直線 \( AB \) の式は \( y=-x+6 \)
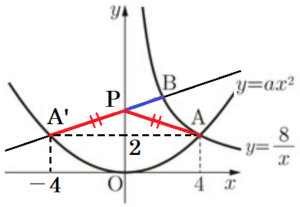
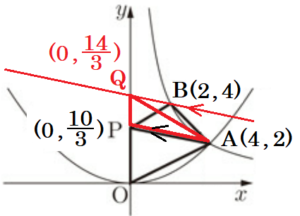
(3) 右の〔図2〕のように,\( y \) 軸上に点 \( P \) を,線分 \( AP \) と線分 \( BP \) の長さの和 \( AP+BP \) がもっとも小さくなるようにとり,\( △ABP \) と \( △APO \) をつくる。
次の①,②の問いに答えなさい。
➀ 点 \( P \) の \( y \) 座標を求めなさい。
【解説】
点 \( A \) を \( y \) 軸に対して対称移動させた点を
\( A’ \) とすると,\( AP=A’P \) になるので,
\( A’P+BP \) がもっとも小さくなるとき。
3点 \( A’,P,B \) は一直線に並びます。
点 \( A’ \) の座標は \( (-4,2) \) なので,
直線 \( A’B \) は,
傾き \( =\dfrac{4-2}{2-(-4)}=\dfrac{1}{3} \)
直線 \( A’B \) の式を \( y=\dfrac{1}{3}x+b \) とすると,
\( B(2,4) \) を通るので,
\( 4=\dfrac{1}{3} \times 2+b \)
\( \dfrac{2}{3}+b=4 \)
\( b=\dfrac{10}{3} \)
よって,点 \( P \) の \( y \) 座標は,\( \dfrac{10}{3} \)
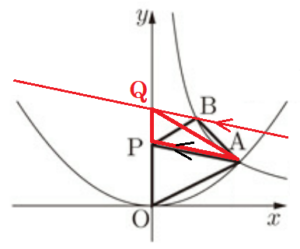
➁ \( △ABP \) の面積を \( S \),\( △APO \) の面積を \( T \) とするとき,\( S:T \) をもっとも簡単な整数の比で表しなさい。
【解説】
\( △ABP \) の面積を直接求めるのは手間がかかりそうなので,等積変形して求めやすくします。
点 \( B \) を通り,線分 \( AP \) と平行な直線と \( y \) 軸との
交点を \( Q \) とすると,
等積変形の考え方から,\( △ABP=△AQP \) に
なっています。
\( △AQP \) の底辺を \( PQ \),\( △AOP \) の底辺を \( OP \)
とすると,高さが等しいので,
\( S:T=PQ:OP \)
になります。
直線 \( AP \) は \( A(4,2),P \left(0,\dfrac{10}{3} \right) \) を通るので,
傾き \( =\dfrac{2-\dfrac{10}{3}}{4-0}=-\dfrac{1}{3} \)
平行な直線の傾きは等しいので,直線 \( BQ \) の式を \( y=-\dfrac{1}{3}x+b \) とすると,
\( B(2,4) \) を通るので,
\( 4=-\dfrac{1}{3} \times 2+b \)
\( -\dfrac{2}{3}+b=4 \)
\( b=\dfrac{14}{3} \)
ここから,点 \( Q \) の座標は,\( Q \left(0,\dfrac{14}{3} \right) \) なので,
\( PQ=\dfrac{14}{3}-\dfrac{10}{3}=\dfrac{4}{3} \)
\( OP=\dfrac{10}{3}-0=\dfrac{10}{3} \)
よって,
\( S:T=PQ:OP=\dfrac{4}{3}:\dfrac{10}{3}=2:5 \)
大問3
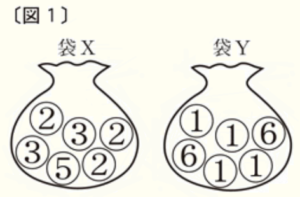
(1) 右の〔 図 1〕のような2つの袋 \( X,Y \) がある。
袋 \( X \) の中には,\( 2 \) の数字が書かれた玉が \( 3 \) 個と,\( 3 \) の数字が書かれた玉が \( 2 \) 個と,\( 5 \) の数字が書かれた玉が \( 1 \) 個入っている。
袋 \( Y \) の中には,\( 1 \) の数字が書かれた玉が \( 4 \) 個と,\( 6 \) の数字が書かれた玉が \( 2 \) 個入っている。
太郎さんと花子さんの2人が,それぞれ次のように2回玉を取り出す。
〔太郎さんの取り出し方〕
・ 1回目は,袋 \( X \) から玉を \( 1 \) 個取り出し,玉に書かれている数字を確認する。
・ 取り出した玉を,袋 \( X \) にもどしてよく混ぜる。
・ 2回目は,ふたたび袋 \( X \) から玉を \( 1 \) 個取り出し,玉に書かれている数字を確認する。
〔花子さんの取り出し方〕
・ 1回目は,袋 \( X \) から玉を \( 1 \) 個取り出し,玉に書かれている数字を確認する。
・ 2回目は,袋 \( Y \) から玉を \( 1 \) 個取り出し,玉に書かれている数字を確認する。
ただし,袋 \( X \) からどの玉を取り出すことも,袋 \( Y \) からどの玉を取り出すことも,それぞれ同様に確からしいものとする。
次の①,②の問いに答えなさい。
➀ 〔太郎さんの取り出し方〕において,1回目に取り出す玉に書かれている数字が,2回目に取り出す玉に書かれている数字より大きくなる確率を求めなさい。
【解答】
\( \dfrac{11}{36} \)
【解説】
袋 \( X \) に入っている玉のうち,
\( 2 \) の数字が書かれた玉 \( 3 \) 個に「 \( 2A,2B,2C \) 」
\( 3 \) の数字が書かれた玉 \( 2 \) 個に「 \( 3A,3B \) 」
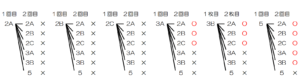
と名前をつけ,それぞれの1回目,2回目の玉の取り出し方の組み合わせを樹形図に書き出し,
1回目の数字の方が2回目の数字よりも大きくなるところに○をつけてみます。
1回目の数字の方が2回目の数字よりも大きくなる組み合わせは \( 11 \) 通り,
すべての組み合わせは \( 36 \) 通りなので,
求める確率は,\( \dfrac{11}{36} \)
➁ 次の(P),(Q)の確率において,確率が大きい方は(P),(Q)のどちらであるか,1つ選び,記号を書きなさい。
また,選んだ方の確率を求めなさい。
(P) 〔太郎さんの取り出し方〕において,1回目に取り出す玉に書かれている数字が,2回目に取り出す玉に書かれている数字より小さくなる確率
(Q) 〔花子さんの取り出し方〕において,1回目に取り出す玉に書かれている数字が,2回目に取り出す玉に書かれている数字より小さくなる確率
【解答】
(Q) \( \dfrac{1}{3} \)
【解説】
(P)
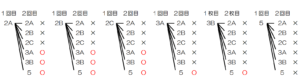
➀のときと同様にそれぞれの1回目,2回目の玉の取り出し方の組み合わせを樹形図に書き出し,
1回目の数字の方が2回目の数字よりも小さくなるところに○をつけてみます。
1回目の数字の方が2回目の数字よりも小さくなる組み合わせは \( 11 \) 通り,
すべての組み合わせは \( 36 \) 通りなので,
求める確率は,\( \dfrac{11}{36} \)
(Q)
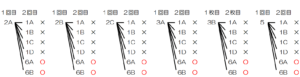
➀のときと同様に袋 \( Y \) に入っている玉にも「 \( 1A,1B,1C,1D,6A,6B \) 」と名前をつけ,
それぞれの1回目,2回目の玉の取り出し方の組み合わせを樹形図に書き出し,
1回目の数字の方が2回目の数字よりも小さくなるところに○をつけてみます。
1回目の数字の方が2回目の数字よりも小さくなる組み合わせは \( 12 \) 通り,
すべての組み合わせは \( 36 \) 通りなので,
求める確率は,\( \dfrac{12}{36}=\dfrac{1}{3} \)
よって,確率が大きいのは(Q)のときで,その確率は \( \dfrac{1}{3} \) になります。
(2) ある中学校の体育大会では,クラス対抗で大縄を跳ぶ競技が行われる。この競技は,\( 5 \) 分間の中で連続して跳んだ回数を競うもので,その回数がもっとも多いクラスが優勝となる。
この中学校3年生の1組から3組までのそれぞれのクラスが,\( 20 \) 日間昼休みに練習を行い,\( 5 \) 分間の中で連続して跳んだ回数の各日の最高回数を記録した。
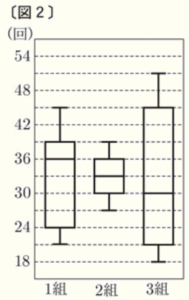
右の〔図2〕は,1組から3組までのそれぞれのクラスが,\( 5 \) 分間の中で連続して跳んだ回数について,各日の最高回数のデータの分布のようすを箱ひげ図にまとめたものである。
次の①,②の問いに答えなさい。
➀ 〔図2〕の箱ひげ図において,1組のデー夕の範囲を求めなさい。
【解説】
範囲は,「最大値 \( – \) 最小値」で求めることができるので,
\( 45-21=24 \)(回)
➁ 〔図2〕の箱ひげ図の特徴をもとに,優勝するクラスを予想する場合,あなたならどのクラスを選ぶか。次の〔説明〕を,下の〔条件〕にしたがって完成させなさい。
〔説明〕
私は, ア 組が優勝すると予想する。
その理由は,箱ひげ図から, ア 組は他の2つのクラスと比べて
イ
〔条件〕
Ⅰ ア には,\( 1,2,3 \) のいずれか1つの数を選んで書くこと。
ただし, \( 1,2,3 \) のどれを選んでもかまわない。
Ⅱ イ には,〔説明〕の続きを,最大値,最小値,中央値のうち,いずれか1つの語句を用い,
用いた語句の数値を示しながら書くこと。
また,用いた語句が,優勝すると予想した根拠となるように書くこと。
【解答】
ア ・・・ \( 1 \)
イ ・・・ 各クラスの中央値は
\( 1 \) 組 ・・・ \( 36 \) 回
\( 2 \) 組 ・・・ \( 33 \) 回
\( 3 \) 組 ・・・ \( 30 \) 回
で \( 1 \) 組 がもっとも大きいため
大問4
太郎さんと花子さんの中学校の修学旅行では,移動には新幹線を利用し,宿泊には旅館を使用することになっている。2人は利用する新幹線と旅館について調べた。
次の(1),(2)の問いに答えなさい。
(1) 太郎さんと花子さんは,新幹線について調べていくうちに,新幹線の車両は,右の〔 図 〕のように通路をはさみ,\( 2 \) 人席と \( 3 \) 人席の両方が設置されていることを知った。
次の会話は,2人が新幹線に設置されている座席について考察しているときのものである。
会話を読んで,下の①,②の問いに答えなさい。
太郎:「新幹線の車両に \( 2 \) 人席と \( 3 \) 人席の両方が設置されていることにより,\( 2 \) 人以上の様々な人数の
グループの利用客が,座席を余らせることなく座ることができる」と聞いたけど,これはどんな意味
なのかな。
花子:例えば,利用客が \( 25 \) 人のグループを考えてみて。\( 25 \) は,\( 2 \) でわっても,\( 3 \) でわっても \( 1 \) 余る
よね。だから,\( 2 \) 人席のみが設置されている車両や \( 3 \) 人席のみが設置されている車両だと \( 1 \) 人
で座る人が出てしまい,座席を余らせてしまうよね。
だけど,\( 2 \) 人席と \( 3 \) 人席の両方が設置されている車両は,\( 3 \) 人席を \( 1 \) 列利用すると,残りは
\( 22 \) 人になるから,\( 2 \) 人席を ア 列利用することで,\( 25 \) 人が座席を余らせることなく座ることが
できるでしょ。
このように,利用客が何人のグループでも,\( 2 \) 人席と \( 3 \) 人席の両方が設置されていると,座席を
余らせることなく座ることができるということだよ。
太郎:なるほど。ということは,これから新幹線の座席を利用するときは,グループの人数を \( 2 \) 人組や
\( 3 \) 人組に分けることができれば,座席を余らせることなく座ることができるということだね。でも,
利用客が \( 25 \) 人の場合,\( 2 \) 人組の数が ア ,\( 3 \) 人組の数が \( 1 \) 以外の組み合わせもありそうだよ。
すべての組み合わせを求めるには,どう考えればいいのかな。
花子:方程式をつくってみようよ。\( 2 \) 人組の数をx,\( 3 \) 人組の数を \( y \) とすると,グループの人数が \( 25 \) 人
だから,2つの文字 \( x \) と \( y \) をふくむ方程式 イ ができるね。
太郎:そうすると,この場合の \( x,y \) は,ともに \( 0 \) 以上の整数だから, イ を成り立たせる \( x \) と
\( y \) の値の組は, \( x= \) ア ,\( y=1 \) をふくめて全部で ウ 組あるね。
➀ 会話中の ア には適する数を, イ には方程式を,それぞれ書きなさい。
【解答】
ア ・・・ \( 11 \)
イ ・・・ \( 2x+3y=25 \)
➁ 会話中の ウ に適する数を求めなさい。
【解説】
全部で \( 25 \) 人なので,必ず \( 3y≦25 \) になります。
\( y \) の値は整数なので,これを満たすのは,\( 0≦y≦7 \) になります。
また,\( 2x \) の値は,\( x \) の値にかかわらず偶数になるので,
\( 3y=25-2x \) より,\( 3y= \) 奇数 \( – \) 偶数であることから,
\( 3y \) の値は必ず奇数になります。
\( 0≦y≦7 \) の範囲で \( 3y \) の値が奇数になるのは,
奇数 \( \times \; y= \) 奇数なので,\( y=1,3,5,7 \) のときになります。
よって,全部で \( 4 \) 組になります。
【偶数と奇数の関係(差)】
偶数 \( – \) 偶数 \( = \) 偶数
偶数 \( – \) 奇数 \( = \) 奇数
奇数 \( – \) 偶数 \( = \) 奇数
奇数 \( – \) 奇数 \( = \) 偶数
【偶数と奇数の関係(積)】
偶数 \( \times \) 偶数 \( = \) 偶数
偶数 \( \times \) 奇数 \( = \) 偶数
奇数 \( \times \) 偶数 \( = \) 偶数
奇数 \( \times \) 奇数 \( = \) 奇数
(2) さらに,太郎さんと花子さんは,宿泊する旅館について調べたところ,この旅館の客室の数と定員は,次のようになっていた。
ただし,客室とは利用客が宿泊する部屋をいい,定員とは1つの客室に宿泊できる人数をいう。
Ⅰ 客室は,1階から4階までにあり,定員が \( 4 \) 名の客室と定員が \( 6 \) 名の客室の2種類のみである。
Ⅱ 1階から4階までのそれぞれの階にある客室の総数は,どの階も同じである。
Ⅲ 1階から4階までのどの階も,定員が \( 4 \) 名の客室の数は,定員が \( 6 \) 名の客室の数の \( 3 \) 倍である。
Ⅳ 1階から4階までのすべての客室の定員の合計は,\( 432 \) 名である。
上のⅠ~Ⅳをもとに,この旅館の1つの階にある定員が \( 4 \) 名の客室と定員が \( 6 \) 名の客室の数を,それぞれ求めなさい。
【解答】
定員 \( 4 \) 名の客室 ・・・ \( 18 \) 部屋
定員 \( 6 \) 名の客室 ・・・ \( 6 \) 部屋
【解説】
1つの階にある定員が \( 4 \) 名の客室の数を \( x \),定員が \( 6 \) 名の客室の数を \( y \) とすると,
1つの階に宿泊できる人数は \( 4x+6y \)(人)と表すことができます。
これが4階分になるので,全部の階で宿泊できる人数の関係を方程式として表すと
\( 4(4x+6y)=432 \) ・・・ ➀
また,定員が \( 4 \) 名の客室の数は,定員が \( 6 \) 名の客室の数の \( 3 \) 倍なので,
これを方程式として表すと \( x=3y \) ・・・ ➁
➀➁を連立方程式として解くと,
\( \left\{ \begin{array}{}
4(4x+6y)=432 \;\; ・・・ \;\; ➀ \\
x=3y \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀を整理すると,
\( 2x+3y=54 \) ・・・ ➀’
➀’に➁を代入すると,
\( 2x+x=54 \)
\( x=18 \)
➁に代入すると,
\( 18=3y \)
\( y=6 \)
大問5
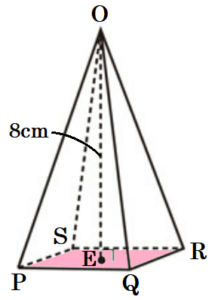
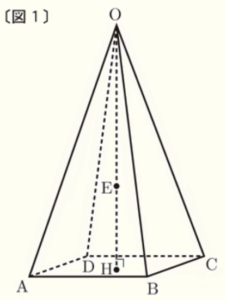
右の〔図1〕のような正四角錐 \( OABCD \) がある。底面 \( ABCD \) は1辺の長さが \( 6 \; cm \) の正方形で,高さ \( OH \) は \( 12 \; cm \) である。
また,\( OE=8 \; cm \) となるように,線分 \( OH \) 上に点Eをとる。
次の(1),(2)の問いに答えなさい。
(1) 正四角錐 \( OABCD \) の体積を求めなさい。
【解説】
\( (6 \times 6) \times 12 \times \dfrac{1}{3}=144 \; (cm^3) \)
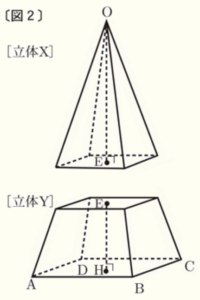
(2) 右の〔図2〕のように,〔図1〕の正四角錐を,点 \( E \) を通り底面 \( ABCD \) に平行な平面で2つの立体に分ける。
このとき,頂点 \( O \) をふくむ方の立体を[立体X],底面 \( ABCD \) をふくむ方の立体を[立体Y]とする。
次の①,②の問いに答えなさい。
➀ [立体X]の体積を求めなさい。
【解答】
\( \dfrac{128}{3} \; cm^3 \)
【解説】
[立体X]の底面を \( IJKL \) とすると,底面 \( ABCD// \)底面 \( IJKL \) なので,
[立体X]と正四角錐 \( OABCD \) は相似になっており,相似比は \( 8:12=2:3 \) になっています。
相似な立体の体積比は相似比の3乗の比と等しいので,
[立体X]\( : \)正四角錐 \( OABCD \) \( =2^3:3^3 \)
[立体X]\( :144=2^3:3^3 \)
[立体X]\( :144=8:27 \)
\( 27 \times \)[立体X]\( =144 \times 8 \)
[立体X]\( =\dfrac{128}{3} \; (cm^3) \)
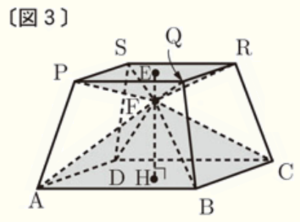
➁ 〔図2〕の[立体Y]において,右の〔図3〕のように,点 \( E \) を通り,底面 \( ABCD \) に平行な面である正方形の頂点を \( P,Q,R,S \) とし,線分 \( EH \) 上に点 \( F \) をとる。
また,点 \( F \) と点 \( A,B,C,D,P,Q,R,S \) をそれぞれ結ぶ。
正四角錐 \( FABCD \) の体積と正四角錐 \( FPQRS \) の体積の和が,①で求めた[立体X]の体積と等しくなるときの線分 \( FH \) の長さを求めなさい。
【解答】
\( \dfrac{16}{5} \; cm \)
【解説】
面 \( PQRS \) は[立体X]の底面と同じ面になっています。
[立体X]は,底面 \( PQRS \) で高さが \( 8 \; cm \) の正四角すいで,
体積が \( \dfrac{128}{3} \; cm^3 \) なので,
底面 \( PQRS \times 8 \times \dfrac{1}{3}=\dfrac{128}{3} \)
底面 \( PQRS \times 8=128 \)
底面 \( PQRS=16 \; (cm^2) \)
〔図3〕において,線分 \( FH=x \; cm \) とすると,
\( OH=12 \; cm,OE=8 \; cm \) より,\( EH=4 \; cm \) であり,
\( EF=(4-x) \; cm \) と表すことができるので,
\( (6 \times 6) \times x \times \dfrac{1}{3}+16 \times (4-x) \times \dfrac{1}{3}=\dfrac{128}{3} \)
\( 36x+16(4-x)=128 \)
\( 20x+64=128 \)
\( x=\dfrac{16}{5} \; (cm) \)
大問6
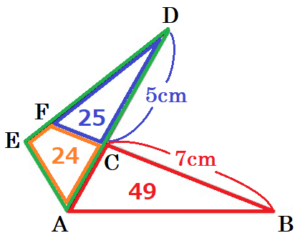
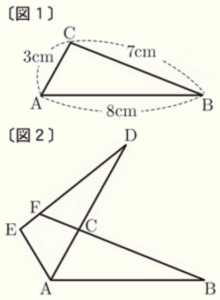
右の〔図1〕のような \( △ABC \) があり,\( AB=8 \; cm,BC=7 \; cm,CA=3 \; cm \) である。
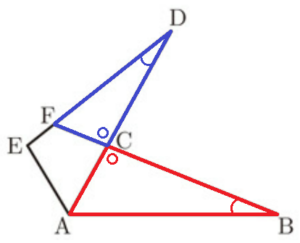
右下の〔図2〕の \( △ADE \) は,〔図1〕の \( △ABC \) を,点 \( A \) を回転の中心として,反時計まわりに \( 60° \) 回転移動させたものである。このとき辺 \( AD \) の一部は辺 \( AC \) と重なっている。
また,線分 \( BC \) を延長した直線と線分 \( DE \) との交点をFとする。
次の(1)~(3)の問いに答えなさい。
(1) \( △ABC \) ∽ \( △FDC \) であることを証明しなさい。
【解答】
\( △ABC \) と \( △FDC \) において,
\( △ADE \) は,\( △ABC \) を回転させたものなので,
\( ∠ABC=∠FDC \) ・・・ ➀
対頂角は等しいので,
\( ∠ACB=∠FCD \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △FDC \)
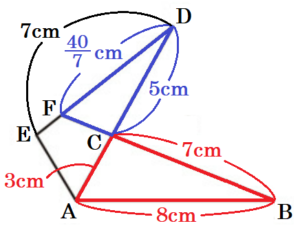
(2) 線分 \( EF \) の長さを求めなさい。
【解答】
\( \dfrac{9}{7} \; cm \)
【解説】
線分 \( EF \) は,線分 \( ED \) から線分 \( FD \) を除いたものであり,
仮定より,\( ED=BC=7 \; cm \) なので,線分 \( FD \) の長さを求めればいいことになります。。
線分 \( FD \) の長さは,(1)より,\( △ABC \) ∽ \( △FDC \) であることを利用すると求められます。
(1)より,\( △ABC \) ∽ \( △FDC \) であり,
\( CD=AD-AC=5 \; cm \) なので,
\( AB:FD=BC:DC \)
\( 8:FD=7:5 \)
\( 7FD=40 \)
\( FD=\dfrac{40}{7} \; (cm) \)
\( ED=7 \; cm \) なので,
\( EF=ED-FD=7-\dfrac{40}{7}=\dfrac{9}{7} \; (cm) \)
(3) 四角形 \( ACFE \) の面積を求めなさい。
【解答】
\( \dfrac{144\sqrt{3}}{49} \; cm^2 \)
【解説】
四角形 \( ACFE \) は,\( △ADE \) から \( △FDC \) を除いたものになっています。
\( △ADE≡△ABC,△ABC \) ∽ \( △FDC \) であることから,
\( △ABC \) の面積を求めればいいことになります。
\( △ABC \) の高さは,三平方の定理を使うことで求められます。
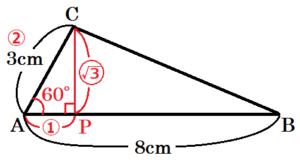
\( △ABC \) において,点 \( C \) から辺 \( AB \) に垂線をひき,交点を点 \( P \) とします。
このとき,\( △ACP \) は,\( ∠CAP=60° \) の
直角三角形なので,
\( AC:CP=2:\sqrt{3} \)
\( 3:CP=2:\sqrt{3} \)
\( CP=\dfrac{3\sqrt{3}}{2} \; (cm) \)
\( △ABC \) の面積は,
\( 8 \times \dfrac{3\sqrt{3}}{2} \times \dfrac{1}{2}=6\sqrt{3} \; (cm^2) \)
\( △ABC \) ∽ \( △FDC \),\( BC=7 \; cm,CD=5 \; cm \) より相似比は \( 7:5 \) であり,
相似な三角形の面積比は相似比の2乗の比と
等しいので,
\( △ABC:△FDC=7^2:5^2=49:25 \)
\( △ADE≡△ABC \) なので,
\( △ADE:△FDC=49:25 \)
\( △ADE=△ABC=6\sqrt{3} \; cm^2 \) なので,
四角形 \( ACFE:△ADE=(49-25):49 \)
四角形 \( ACFE:6\sqrt{3}=24:49 \)
四角形 \( ACFE \times 49=24 \times 6\sqrt{3} \)
四角形 \( ACFE=\dfrac{144\sqrt{3}}{49} \; (cm^2) \)




-300x246.png)