大問1
(1) \( -5-(-7) \)
【解説】
\( =-5+7 \)
\( =2 \)
(2) \( (-12) \div \dfrac{4}{3} \)
【解説】
\( =-12 \times \dfrac{3}{4} \)
\( =-9 \)
(3) \( 7-5 \times (-2) \)
【解説】
\( =7-(-10) \)
\( =7+10 \)
\( =17 \)
(4) \( \sqrt{12}+\sqrt{27} \)
【解説】
\( =2\sqrt{3}+3\sqrt{3} \)
\( =5\sqrt{3} \)
(5) \( (-3a)^2 \times (-2b) \)
【解説】
\( =9a^2 \times (-2b) \)
\( =-18a^2b \)
(6) \( 3(5x+2y)-4(3x-y) \)
【解説】
\( =15x+6y-12x+4y \)
\( =3x+10y \)
大問2
(1) 一次方程式 \( 5x-6=2x+3 \) の解は,\( x= \) である。
【解説】
\( 3x=9 \)
\( x=3 \)
(2) 連立方程式 \( \left \{ \begin{array}{}
2x+y=5 \\
x-2y=5
\end{array} \right. \) の解は,\( x= \) ,\( y= \) である。
【解説】
\( 2x+y=5 \) ・・・ ➀
\( x-2y=5 \) ・・・ ➁
➀\( \times 2 \) すると,
\( 4x+2y=10 \) ・・・ ➀’
➀’+➁すると,
\( 5x=15 \)
\( x=3 \)
➀に代入すると,
\( 2 \times 3+y=5 \)
\( 6+y=5 \)
\( y=-1 \)
(3) \( (x+3)(x-3) \) を展開して整理すると, である。
【解説】
和と差の積の公式 \( (a+b)(a-b)=a^2-b^2 \) より,
\( (x+3)(x-3)=x^2-9 \)
(4) \( x^2+2x-15 \) を因数分解すると, である。
【解説】
\( (x+a)(x+b)=x^2+(a+b)x+ab \) より,
足して \( 2 \),かけて \( -15 \) になる \( a,b \) の組み合わせは,
\( a=−3,b=5 \) なので,\( (x−3)(x+5) \)
(5) 二次方程式 \( 2x^2+5x+1=0 \) の解は,\( x= \) である。
【解答】
\( \dfrac{-5± \sqrt{17}}{4} \)
【解説】
\( ax^2+bx+c=0 \) と考えると,\( a=2,b=5,c=1 \) なので,
解の公式から,
\( x=\dfrac{-5±\sqrt{5^2-4 \times 2 \times 1}}{2 \times 2} \)
\( =\dfrac{-5± \sqrt{17}}{4} \)
(6) \( \sqrt{5}<n<\sqrt{11} \) となるような自然数 \( n \) の値は,\( n= \) である。
【解説】
\( \sqrt{5}<n<\sqrt{11} \) の各辺を2乗すると,\( 5<n^2<11 \)
\( n=2 \) のとき,\( 2^2=4 \),
\( n=3 \) のとき,\( 3^2=9 \),
\( n=4 \) のとき,\( 4^2=16 \) なので,
\( 5<n^2<11 \) にあてはまる \( n \) の値は,\( n=3 \)
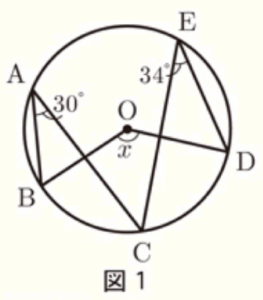
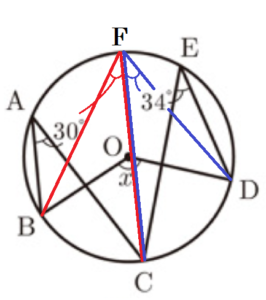
(7) 右の図1のように円 \( O \) の周上に,5点 \( A,B,C,D,E \) があるとき,\( ∠x= \) °である。
【解説】
弧 \( AE \) 上に点 \( F \) をとると,
弧 \( BC \) の円周角なので \( ∠BFC=∠BAC=30° \)
弧 \( CD \) の円周角なので \( ∠CFD=∠CED=34° \)
\( ∠BFD \) は弧 \( BD \) の円周角,\( ∠BOD \) は弧 \( BD \) の中心角なので,
\( ∠BOD=2∠BFD=2(30°+34°)=128° \)
(8) 1個120円のメロンパンが10%値上がりした。このメロンパンを3個買うとき,代金は 円である。ただし,消費税は考えないものとする。
【解説】
1個120円のメロンパンが10%値上がりしたときの価格は,\( 120 \times 1.1=132 \)(円) なので,
このメロンパンを3個買うと,\( 132×3=396 \)(円)
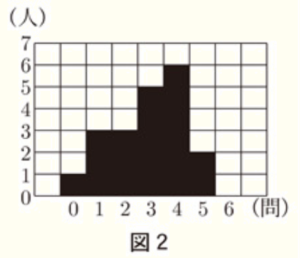
(9) 右の図2のグラフは,あるクラスの生徒20人にクイズを6問出し,クイズに正解した問題数と人数の関係を表したものである。20人がクイズに正解した問題数について次の ア~ウ の代表値を求めたとき,その値が最も大きいものは である。 次の ア~ウ のうちから1つ選び,記号で答えなさい。
ア 平均値 イ 中央値 ウ 最頻値
【解説】
平均値 ・・・ \( \dfrac{0 \times 1+1 \times 3+2 \times 3+3 \times 5+4 \times 6+5 \times 2}{20}=2.9 \)(回)
中央値 ・・・ 正解数が少ない方から10番目と11番目の人のどちらも3問なので,中央値は3問
最頻値 ・・・ 度数が最も大きい階級は4回
大問3
那覇市に住む太郎さんは,2019年から2022年までの4年間について那覇市の気温のデータを調べてみた。下の表は,それぞれの年の5月の31日間について,日最高気温のデータをまとめたもので,図はそのデータをもとに箱ひげ図に表したものである。
このとき,次の各問いに答えなさい。
ただし,日最高気温とは,1日の中での最高気温のことである。

問1 2022年5月の日最高気温を表す箱ひげ図を上の図のA~Dのうちから1つ選び,記号で答えなさい。
【解説】
表で各年の最大値を見てみると,2022年だけが30℃未満になっています。
A~Dのうち,最大値が30℃未満になっているのは,B
問2 2020年5月の日最高気温の範囲を求めなさい。
【解説】
範囲は,最大値 – 最小値 で求めることができます。
最大値は \( 30.7 \) ℃,最小値は \( 22.7 \) ℃ なので,\( 30.7−22.7=8.0 \) (℃)
問3 那覇市の5月の日最高気温について,上の表および図から読み取れるものを,次のア~エのうちから1つ選び,記号で答えなさい。
ア 2022年の四分位範囲は,他の年の四分位範囲と比べて最も大きい。
イ 2022年は,日最高気温が25℃以下の日数が7日以上あった。
ウ 2022年は,日最高気温が30℃を超えた日があった。
エ どの年も日最高気温の平均値は,中央値よりも小さい。
【解説】
ア 四分位範囲は,第三四分位数 – 第一四分位数 で求めることができます。
2019年 ・・・ \( 28.1−25.7=2.4 \) (℃)
2020年 ・・・ \( 29.4−26.6=2.8 \) (℃)
2021年 ・・・ \( 30.3−27.0=3.3 \) (℃)
2022年 ・・・ \( 27.4−24.4=3.0 \) (℃)
イ データの総数が31個なので,第一四分位数にあたるのは,小さい方から8番目の値になります。
2022年の第一四分位数は,\( 24.4 \) ℃ なので,25℃以下の日数が7日以上あったといえます。
ウ 2022年は,最大値が \( 29.9 \) ℃ なので,30℃を超えた日はない。
エ 表より,2019年は,平均値の方が中央値よりも大きい。
大問4
2つのさいころA,Bを同時に投げる。Aの出た目の数を十の位,Bの出た目の数を一の位として2けたの整数 \( n \) をつくる。
このとき,次の各問いに答えなさい。
ただし,どちらのさいころも1から6までの目の出方は,同様に確からしいものとする。
問1 整数 \( n \) は全部で何通りできるか求めなさい。
【解説】
できる整数は,\( 11,12,13,14,15,16,21,22,23,24,25,26, \)
\( 31,32,33,34,35,36,41,42,43,44,45,46, \)
\( 51,52,53,54,55,56,61,62,63,64,65,66 \)
の36通り
問2 \( n≧55 \) となる確率を求めなさい。
【解説】
問1の36通りのうち,\( n≧55 \) となるのは \( 55,56,61,62,63,64,65,66 \) の8通りなので,
求める確率は,\( \dfrac{8}{36}=\dfrac{2}{9} \)
問3 整数 \( n \) が3の倍数となる確率を求めなさい。
【解説】
問1の36通りのうち,\( n \) が3の倍数となるのは,
\( 12,15,21,24,33,36,42,45,51,54,63,66 \) の12通りなので,
求める確率は,\( \dfrac{12}{36}=\dfrac{1}{3} \)
大問5
ある電話会社には,1か月の電話使用料金について,次のようなA,B,Cの3種類の料金プランがある。
ただし,1か月の電話使用料金は基本料金と通話料金の合計金額とする。
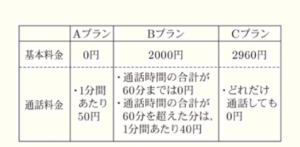
このとき,次の各問いに答えなさい。
ただし,消費税は考えないものとする。
問1 Aプランで1か月に \( x \) 分通話したときの電話使用料金を \( y \) 円とするとき,\( y \) を \( x \) の式で表しなさい。
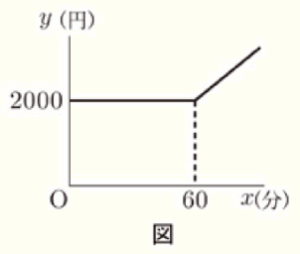
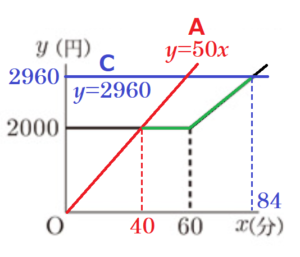
問2 右の図はBプランで1か月に x 分通話したときの電話使用料金を \( y \) 円として \( x \) と \( y \) の関係をグラフに表したものである。Bプランで1か月に80分通話したときの電話使用料金を求めなさい。
【解説】
60分から80分までの20分間に対して,1分間あたり40円の通話料金がかかるので,
\( 20×40=800 \)(円)。これに,基本料金2000円を加えて,2800円になります。
問3 花子さんは,「私にとっては3種類の料金プランのうちBプランであると電話使用料金が最も安くなります。」と話している。花子さんの1か月の通話時間は何分から何分までの間と考えられるか,答えなさい。
【解説】
問2のグラフにAプランとCプランの直線を書きたすと
右の図のようになります。
このグラフの中でBプランが最も安くなるのは,
Bプランを表す黒の線が一番下にくるときです。
これにあてはまるのは,緑で色を付けた部分になります。
Aプランを表す赤の直線の式は \( y=50x \) なので,
黒の直線と交わるとき,つまり,\( y=2000 \) になるときの
\( x \) の値は,
\( 2000=50x \)
\( x=40 \)
Cプランを表す青の直線の式は \( y=2960 \) なので,
黒の直線と交わるとき,
つまり,黒の直線の \( y \) の値が \( y=2960 \) になるとき,
基本料金以外にかかる通話料金は,\( 2960−2000=960 \)(円)になります。
1分間当たりの通話料金は40円なので,
追加料金がかかるのは \( \dfrac{960}{40}=24 \)(分)
よって,\( y=2960 \) になるときの \( x \) の値は,\( x=60+24=84 \)
以上より,Bプランが最も安くなるのは40分から84分の間になります。
大問6
結奈さんと琉斗さんは,連続する2つの奇数では,大きい奇数の2乗から小さい奇数の2乗をひいた数がどんな数になるか調べた。
\( 1,3 \) のとき \( 3^2−1^2=9−1=8 \)
\( 3,5 \) のとき \( 5^2−3^2=25−9=16 \)
\( 5,7 \) のとき \( 7^2−5^2=49−25=24 \)
結奈さんは,これらの結果から次のことを予想した。
<結奈さんの予想>
連続する2つの奇数では,大きい奇数の2乗から小さい奇数の2乗をひいた数は8の倍数になる。
上記の <結奈さんの予想> がいつでも成り立つことは,次のように証明できる。
(証明)
\( n \) を整数とすると,連続する2つの奇数は
\( 2n+1,2n+3 \)
と表せる。 大きい奇数の2乗から小さい奇数の2乗をひいた数は
\( (2n+3)^2−(2n+1)^2 \)
\( =4n^2+12n+9−(4n^2+4n+1) \)
\( =8n+8 \)
\( =8(n+1) \)
\( n+1 \) は整数だから,\( 8(n+1) \) は8の倍数である。
したがって,連続する2つの奇数では,大きい奇数の2乗から
小さい奇数の2乗をひいた数は8の倍数になる。
次の各問いに答えなさい。
問1 二人は,「連続する2つの奇数」を「連続する2つの偶数」に変えたとき,どんな数になるかを調べることにした。琉斗さんは,いくつか計算した結果から次のことを予想した。 にあてはまることばを答えなさい。
<琉斗さんの予想>
連続する2つの偶数では,大きい偶数の2乗から小さい偶数の2乗をひいた数は になる。
問2 問1の <琉斗さんの予想> がいつでも成り立つことを証明しなさい。
【解答】
\( n \) を整数とすると,連続する2つの偶数は
\( 2n,2n+2 \)
と表せる。 大きい奇数の2乗から小さい奇数の2乗をひいた数は
\( (2n+2)^2−(2n)^2 \)
\( =4n^2+8n+4−4n^2 \)
\( =8n+4 \)
\( =4(2n+1) \)
\( 2n+1 \) は整数だから,\( 4(2n+1) \) は4の倍数である。
したがって,連続する2つの偶数では,大きい偶数の2乗から
小さい偶数の2乗をひいた数は4の倍数になる。
大問7
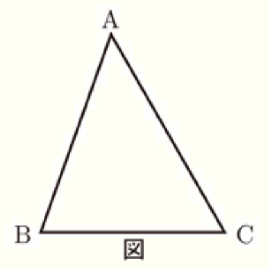
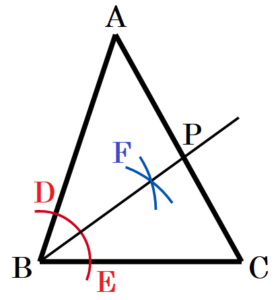
右の図のような \( ∠B=70° \) の \( △ABC \) がある。
辺 \( AC \) 上に \( ∠ABP=35° \) となるような点 \( P \) を定規とコンパスを使って作図しなさい。
ただし,点を示す記号 \( P \) をかき入れ,作図に用いた線は消さずに残しておくこと。
【解答】
\( ∠B=70°,∠ABP=35° \) より,線分 \( BP \) は \( ∠B \) の二等分線になります。
手順1 点 \( B \) を中心に線分 \( AB,BC \) と交わるように弧を描く。
(交点を点 \( D,E \) とします)
手順2 点 \( D,E \) を中心に弧を描く。
(交点を点 \( F \) とします)
手順3 点 \( B,F \) を通る直線を描く。
手順3の直線と線分 \( AC \) の交点が作図する点 \( P \) になります。
大問8
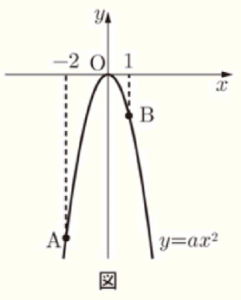
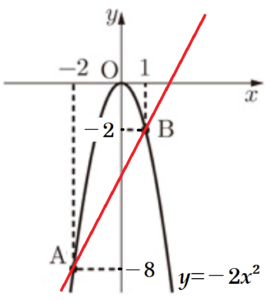
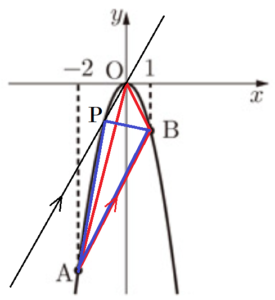
右の図のように,関数 \( y=ax^2 \) のグラフ上に2点 \( A,B \) があり,\( x \) 座標はそれぞれ \( -2,1 \) である。
また、この関数は,\( x \) の値が \( -2 \) から \( 1 \) まで増加するときの変化の割合は \( 2 \) である。
このとき,次の各問いに答えなさい。
問1 \( a \) の値は次のように求めることができる。
下の (1),(2) にあてはまる数や式を答えなさい。
関数 \( y=ax^2 \) について
\( x=-2 \) のとき,\( y= \) (1) である。
\( x=1 \) のとき,\( y=a \) である。
よって,変化の割合が \( 2 \) であることから,
\( a \) の値は (2) である。
【解答】
(1) ・・・ \( 4a\)
(2) ・・・ \( -2\)
【解説】
\( y=ax^2 \) に \( x=-2 \) を代入すると,\( y=a \times (-2)^2=4a \)
変化の割合は,\( \dfrac{a-4a}{1-(-2)}=\dfrac{-3a}{3}=−a \)
よって,
\( -a=2 \)
\( a=-2 \)
問2 2点 \( A,B \) を通る直線の式を求めなさい。
【解説】
問1より,\( a=-2 \) なので,\( B \) の \( y \) 座標は,\( y=-2 \) であり, \( B(1,-2) \)
2点 \( A,B \) を通る直線の傾きは \( 2 \) なので,
この直線の式を \( y=2x+b \) とし,\( x=1,y=-2 \) を代入すると,
\( -2=2×1+b \)
\( b=-4 \)
よって,求める直線の式は,\( y=2x-4 \)
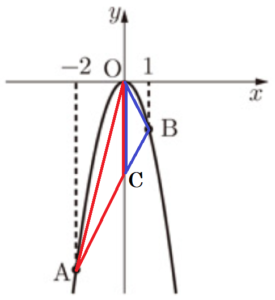
問3 \( △OAB \) の面積を求めなさい。
【解説】
線分 \( AB \) と \( y \) 軸の交点を点 \( C \) とし,
\( △OAC \) と \( △OBC \) に分けて考えます。
問2より,\( C \) の \( y \) 座標は \( -4 \) なので,
線分 \( OC \) を底辺と考えると,
\( △OAC \) は,底辺が \( 4 \),高さが \( 2 \),
\( △OBC \) は,底辺が \( 4 \),高さは \( 1 \) なので,
\( △OAB=△OAC+△OBC \)
\( =\left(4 \times 2 \times \dfrac{1}{2} \right)+\left(4 \times 1 \times \dfrac{1}{2} \right) \)
\( =4+2 \)
\( =6 \)
問4 関数 \( y=ax^2 \) のグラフ上に \( x \) 座標が \( t \) である点 \( P \) をとると,\( △PAB \) の面積と \( △OAB \) の面積が等しくなった。
このとき,点 \( P \) の座標を求めなさい。ただし,点 \( P \) は原点 \( O \) と異なり,\( -2≦t≦1 \) とする。
【解説】
\( △PAB \) と \( △OAB \) は辺 \( AB \) が共通なので,
等積変形の考え方から,\( OP//AB \) のとき,\( △PAB \) と \( △OAB \) の面積が等しくなります。
直線 \( AB \) の傾きは \( 2 \) なので,直線 \( OP \) の式は,\( y=2x \)
よって,点 \( P \) は \( y=-2x^2 \) と \( y=2x \) の交点になるので,
\( -2x^2=2x \)
\( 2x^2+2x=0 \)
\( x^2+x=0 \)
\( x(x+1)=0 \)
\( x=0,-1 \)
\( -2≦t≦1 \) なので,あてはまる \( x \) の値は \( x=-1 \)
\( y=2x \) に代入すると,\( y=-2 \)
以上より,\( P(-1,-2) \)
大問9
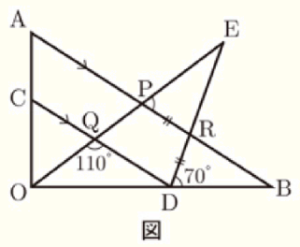
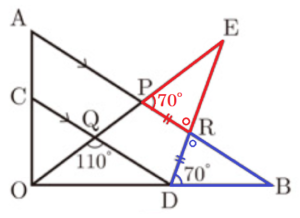
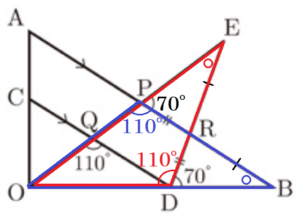
図のように,\( △OAB \) があり,辺 \( OA \) 上に点 \( C \) をとる。点 \( C \) を通り,辺 \( AB \) に平行な直線と辺 \( OB \) との交点を点 \( D \) とする。また,下の図のような点 \( E \) をとり,線分 \( EO \) と辺 \( AB \),線分 \( CD \) との交点をそれぞれ点 \( P \),点 \( Q \) とし,線分 \( ED \) と辺 \( AB \) との交点を点 \( R \) とする。
このとき, \( RP=RD,∠OQD=110° \),
\( ∠BDR=70° \) であった。次の各問いに答えなさい。
問1 \( ∠EPR \) を求めなさい。
【解説】
\( ∠EQD=180°−∠OQD=70° \) なので,
\( AB//CD \) より,\( ∠EPR=∠EQD=70° \)
問2 \( △REP \) と \( △RBD \) が合同であることを証明しなさい。
【解答】
\( △REP \) と \( △RBD \) において,
問1より,\( ∠EPR=70° \) ・・・ ➀
仮定より,\( ∠BDR=70° \) ・・・ ➁
➀➁より,\( ∠EPR=∠BDR \) ・・・ ➂
仮定より,\( RP=RD \) ・・・ ➃
対頂角は等しいので,\( ∠ERP=∠BRD \) ・・・ ➄
➂➃➄より,1組の辺とその両端の角がそれぞれ等しいので,\( △REP≡△RBD \)
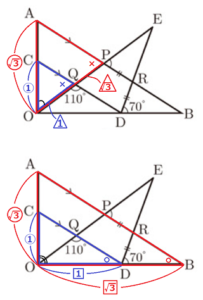
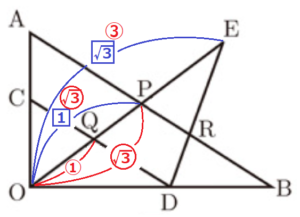
問3 \( OA:OC=\sqrt{3}:1 \) のとき,\( OQ:QE \) を求めなさい。
【解説】
\( △OAP \) と \( △OCQ \) において,
\( AB//CD \) より,同位角は等しいので,\( ∠OPA=∠OQC \)
また,\( ∠Q \) は共通なので,
2組の角がそれぞれ等しいので,\( △OAP \) ∽ \( △OCQ \)
対応する辺の比は等しいので,
\( OP:OQ=OA:OC=\sqrt{3}:1 \)
\( △OAB \) と \( △OCD \) においても同様に
\( △OAB \) ∽ \( △OCD \) なので,
\( OB:OD=OA:OC=\sqrt{3}:1 \)
\( △ODE≡△OPB \) であり,\( OE=OB,OD=OP \) なので,
\( OE:OP=OB:OD=\sqrt{3}:1=3:\sqrt{3} \) ・・・ ➀
また, \( OP:OQ=\sqrt{3}:1 \) ・・・ ➁ なので,
➀➁より,\( OE:OP:OQ=3:\sqrt{3}:1 \)
ここから,\( OQ:OE=1:3 \)
よって,
\( OQ:QE=OQ:(OE−OQ)=1:2 \)
△ODE≡△OPBの証明
\( △ODE \) と \( △OPB \) において,
\( ∠ODE=180°−∠BDR=110° \) ・・・ ➀
\( AB//CD \) より,同位角は等しいので,
\( ∠OPB=∠OQD=110° \) ・・・ ➁
➀➁より,\( ∠ODE=∠OPB=110° \) ・・・ ➂
問2より,\( △REP≡△RBD \) なので,
\( ∠OED=∠OBP \) ・・・ ➃
\( ER=BR \) ・・・ ➄
仮定より,\( RP=RD \) ・・・ ⑥
➄➅より,
\( ER+RD=BR+RP \)
\( ED=BP \) ・・・ ⑦
➂➃⑦より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △ODE≡△OPB \)
大問10
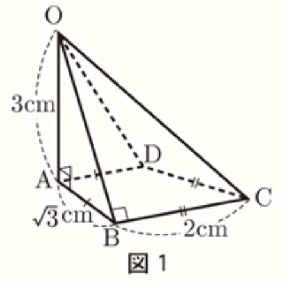
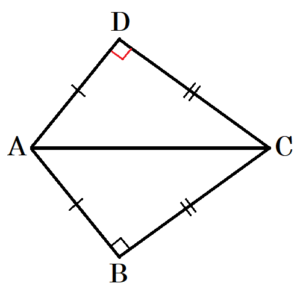
右の図1の四角すい \( OABCD \) において,面 \( ABCD \) は
\( AB=AD= \sqrt{3} \; cm,BC=CD=2 \; cm \) の四角形である。
また,辺 \( OA \) は面 \( ABCD \) と垂直で,\( OA=3 \; cm \),
\( ∠OBC=90° \) である。
このとき,次の各問いに答えなさい。
問1 辺 \( OB \) の長さを求めなさい。
【解答】
\( 2\sqrt{3} \; cm \)
【解説】
\( △OAB \) において,三平方の定理より,
\( OB^2=3^2+( \sqrt{3} )^2=12 \)
\( OB=2\sqrt{3} \; (cm) \) (\( OB>0 \)より)
問2 四角すい \( OABCD \) において,\( △OBC \) や \( △QAC \) で三平方の定理を利用することにより, \( AC=\sqrt{7} \; cm \) であることが分かった。
このことによって,分かることがらとして正しくないものを,次のア~エのうちから1つ選び,記号で答えなさい。
ア \( ∠ABC=90° \) である。
イ 線分 \( AC \) は,3点 \( A,B,C \) を通る円の直径である。
ウ 四角形 \( ABCD \) は台形である。
エ 点 \( D \) は,3点 \( A,B,C \) を通る円の周上にある。
【解説】
ア \( △ABC \) において,
\( AC^2=AB^2+BC^2 \)
\( (\sqrt{7})^2=(\sqrt{3})^2+2^2 \)
が成り立つので,\( ∠ABC=90° \) である。
イ 直径に対する円周角は \( 90° \) になるので,\( △ABC \) が \( ∠B=90° \) の直角三角形であることから,
線分 \( AC \) は,3点 \( A,B,C \) を通る円の直径である。
エ \( △ABC \) と \( △ADC \) において,
\( AB=AD,BC=DC,AC \)共通 より,
3組の辺がそれぞれ等しいので,\( △ABC≡△ADC \)
対応する角は等しいので,\( ∠ADC=∠ABC=90° \)
よって,イと同様に,\( ∠D \) は直径 \( AC \) に対する円周角です。
ここから,点 \( D \) も線分 \( AC \) を直径とする円上の点といえます。
ウ 台形は向かい合う1組の辺が平行な四角形なので,
四角形 \( ABCD \) が台形であるとき,\( AB//CD,AD//BC \) が少なくとも1つは成り立ちます。
このとき,\( ∠B=90° \) より,\( ∠BAD=90°,∠BCD=90° \) のどちらかは成り立つ必要があります。
エ より,四角形 \( ABCD \) は,線分 \( AC \) を直径とする円に内接するので,
向かい合う角の和は \( 180° \) になります。
ここで,\( ∠BAD=90° \) と仮定すると,\( ∠BCD \) も \( 90° \) になりますが,
\( AB=AD=\sqrt{3} \; cm,BC=CD=2 \; cm \) より,線分 \( BD \) の長さが等しくなりません。
よって,\( ∠BAD \) も \( ∠BCD \) も \( 90° \) ではなく,\( AB//CD,AD//BC \) はどちらも成り立ちません。
よって,四角形 \( ABCD \) は台形ではありません。
問3 四角すい \( OABCD \) の体積を求めなさい。
【解答】
\( 2\sqrt{3} \; cm^3 \)
【解説】
\( △ABC≡△ADC \) より,四角形 \( ABCD=2△ABC \)
よって,求める体積は,
四角形 \( ABCD \times OA \times \dfrac{1}{3} \)
\( =\left(\sqrt{3} \times 2 \times \dfrac{1}{2} \times 2 \right) \times 3 \times \dfrac{1}{3} \)
\( =2\sqrt{3} \; (cm^3) \)
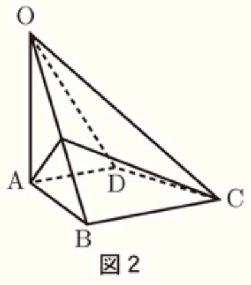
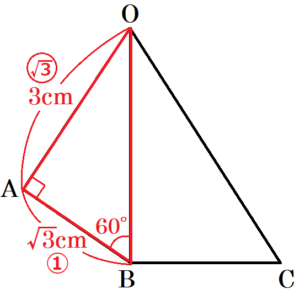
問4 右の図2のように,図1の四角すい \( OABCD \) の表面に,点 \( A \) から辺 \( OB \) を通って点 \( C \) まで糸をかける。かける糸の長さが最も短くなるときの糸の長さを求めなさい。
【解答】
\( \sqrt{13} \; cm \)
【解説】
面 \( △OAB \) と面 \( △OBC \) を右の図のように展開するとき,
\( AC \) 間の距離が最も短くなるのは,\( AC \) 間を直線で結ぶときなので,線分 \( AC \) の長さを求めます。
\( AB=\sqrt{3} \; cm,OA=3 \; cm,OA⊥AB \) より,
\( AB:OA=\sqrt{3}:3=1:\sqrt{3} \) なので,
\( △OAB \) は,3辺の比が \( 1:2:\sqrt{3} \) の直角三角形なので,
\( ∠OBA=60° \)
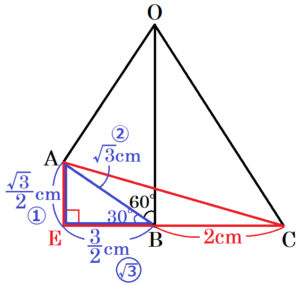
点 \( A \) から辺 \( BC \) の延長線に垂線をひき,交点を点 \( E \) とすると,
\( ∠OBE=90°,∠OBA=60° \) より,\( ∠ABE=30° \) なので,
\( △ABE \) は,3辺の比が \( 1:2:\sqrt{3} \) の直角三角形です。
よって,\( AB=\sqrt{3} \; cm \) より,\( AE=\dfrac{\sqrt{3}}{2} \; cm,BE=\dfrac{3}{2} \; cm \)
\( △ACE \) において,三平方の定理より,
\( AC^2=AE^2+CE^2 \)
\( =\left(\dfrac{\sqrt{3}}{2} \right)^2+\left(\dfrac{3}{2}+2 \right)^2 \)
\( =\dfrac{3}{4}+\dfrac{49}{4} \)
\( =\dfrac{52}{4} \)
\( AC=\dfrac{2 \sqrt{13}}{2}= \sqrt{13} \; (cm) \) (\(AC>0\)より)
大問11
正 \( n \) 角形のそれぞれの辺上に頂点から頂点までに,ある規則にしたがって碁石を並べる。
このとき,次の各問いに答えなさい。
ただし,\( n \) は3以上の自然数とする。
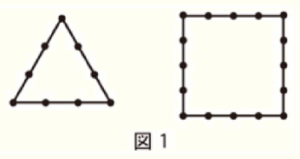
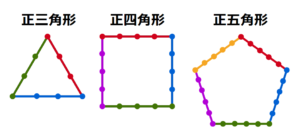
[規則1] 正 \( n \) 角形のそれぞれの辺上に頂点から頂点までを \( n \) 等分するように碁石を等間隔に並べる。
図1は [規則1] にしたがって,正三角形と正四角形の辺上に碁石を並べたものである。
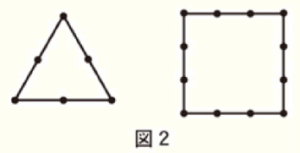
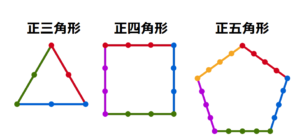
[規則2] 正 \( n \) 角形のそれぞれの辺上に頂点から頂点までの碁石の個数が,ちょうど \( n \) 個となるように
碁石を等間隔に並べる。
図2は [規則2] にしたがって,正三角形と正四角形の辺上に碁石を並べたものである。
問1 [規則1] にしたがって,正五角形の辺上に碁石を並べるときに必要な碁石の個数を求めなさい。
問2 [規則1] にしたがって,正 \( n \) 角形の辺上に碁石を並べるときに必要な碁石の個数を \( n \) を使った式で表しなさい。
【解説】
例として,正三角形,正四角形,正五角形について,それぞれ必要な碁石の数の規則性を考えます。
正三角形 ・・・ 3本の辺に3個ずつ並べるので,\( 3 \times 3=9 \)(個)
正四角形 ・・・ 4本の辺に4個ずつ並べるので,\( 4 \times 4=16 \)(個)
正五角形 ・・・ 5本の辺に5個ずつ並べるので,\( 5 \times 5=25 \)(個)
よって,
正 \( n \) 角形 ・・・ \( n \) 本の辺に \( n \) 個ずつ並べるので, \( n \times n=n^2 \)(個)
問3 [規則2] にしたがって碁石を並べるときに必要な碁石の個数を調べる。必要な碁石の個数は,正三角形で6個,正四角形で12個である。必要な碁石の個数が870個となるのは正何角形であるか答えなさい。
【解説】
例として,正三角形,正四角形,正五角形について,それぞれ必要な碁石の数の規則性を考えます。
正三角形 ・・・ 3本の辺に2個ずつ並べるので,\( 3 \times 2=6 \)(個)
正四角形 ・・・ 4本の辺に3個ずつ並べるので,\( 4 \times 3=12 \)(個)
正五角形 ・・・ 5本の辺に4個ずつ並べるので,\( 5 \times 4=20 \)(個)
よって,
正 \( n \) 角形 ・・・ \( n \) 本の辺に \( n-1 \) 個ずつ並べるので, \( n \times n−1=n(n−1) \)(個)
ここで,\( 870=30 \times 29 \) なので,必要な碁石の個数が870個となるのは正三十角形のとき。
870=30×29を方程式を解かずに求める方法
\( 870 \) は,\( 900=30 \times 30 \) に近い数なので,\( n \) は \( 30 \) またはそれに近い数であると推測できます。 碁石の数を表す式は \( n(n−1) \) なので,\( 30×29 \) で試してみると,\( 870 \) になることがわかります。
この方法は「\( n^2≦500 \) を満たす \( n \) のうち最も大きい値を求めなさい」のような問題にも使えます。