大問1
(1) \( 2 \times (-3)-4^2 \)
【解説】
\( =-6-16 \)
\( =-22 \)
(2) \( 5(2a+b)-4(a+3b) \)
【解説】
\( =10a+5b-4a-12b \)
\( =6a-7b \)
(3) \( 2a \times 9ab \div 6a^2 \)
【解説】
\( =\dfrac{2a \times 9ab}{6a^2} \)
\( =3b \)
(4) \( (x+1)^2+x(x-2) \)
【解説】
\( =x^2+2x+1+x^2-2x \)
\( =2x^2+1 \)
(5) \( (2\sqrt{5}+\sqrt{3}) (2\sqrt{5}-\sqrt{3}) \)
【解説】
\( =(2\sqrt{5})^2-\sqrt{3}^2 \)
\( =20-3 \)
\( =17 \)
大問2
(1) \( a=-6,b=5 \) のとき,\( a^2-8b \) の値を求めなさい。
【解説】
\( a^2-8b \) に \( a=-6,b=5 \) を代入すると,
\( a^2-8b=(-6)^2-8 \times 5 \)
\( =36-40 \)
\( =-4 \)
(2) 二次方程式 \( x^2-11x+18=0 \) を解きなさい。
【解説】
\( (x-2)(x-9)=0 \)
\( x=2,9 \)
(3) \( n \) を自然数とするとき,\( 5-\dfrac{78}{n} \) の値が自然数となるような最も小さい \( n \) の値を求めなさい。
【解説】
\( 5-\dfrac{78}{n} \) の値が自然数になるためには,\( 5-\dfrac{78}{n}>0 \) より,
\( \dfrac{78}{n} \) の値が \( 5 \) 未満の自然数でなければなりません。
また,\( n \) は自然数なので,\( \dfrac{78}{n} \) の値は正の数になります。
よって,\( 0<\dfrac{78}{n}<5 \) の自然数になります。
\( \dfrac{78}{n} \) の値が自然数であるとき,\( n \) は \( 78 \) の約数になります。
\( 78 \) の約数は,\( 1,2,3,6,13,26,39,78 \) なので,
\( n=78 \) のとき,\( \dfrac{78}{n}=1 \)
\( n=39 \) のとき,\( \dfrac{78}{n}=2 \)
\( n=26 \) のとき,\( \dfrac{78}{n}=3 \)
\( n=13 \) のとき,\( \dfrac{78}{n}=6 \) → \( 5 \) より大きいのであてはまらない
以下,\( 1,2,3,6 \) の場合は,すべて \( \dfrac{78}{n} \) の値が \( 5 \) より大きくなるので,あてはまりません。
よって,\( 0<\dfrac{78}{n}<5 \) の自然数になる最も小さい \( n \) の値は,\( n=26 \)
(4) 関数 \( y=\dfrac{10}{x} \) について,\( x \) の値が \( 1 \) から \( 5 \) まで増加するときの変化の割合を求めなさい。
【解説】
\( x=1 \) のとき,\( y=\dfrac{10}{1}=10 \)
\( x=5 \) のとき,\( y=\dfrac{10}{5}=2 \)
なので,変化の割合は,\( \dfrac{2-10}{5-1}=-2 \)
(5) 二つの箱A,Bがある。箱Aには自然数の書いてある3枚のカード \( \fbox{1},\fbox{2},\fbox{3} \) が入っており,箱Bには奇数の書いてある5枚のカード \( \fbox{1},\fbox{3},\fbox{5},\fbox{7},\fbox{9} \) が入っている。A,Bそれぞれの箱から同時にカードを1枚ずつ取り出し, 箱Aから取り出したカードに書いてある数を \( a \),箱Bから取り出したカードに書いてある数を \( b \) とする。このとき,\( \dfrac{b}{a} \) の値が \( 1 \) より大きく \( 4 \) より小さい数になる確率はいくらですか。A,Bそれぞれの箱において, どのカードが取り出されることも同様に確からしいものとして答えなさい。
【解説】
A,Bそれぞれの箱から取り出したカードの組み合わせとそのときの \( \dfrac{b}{a} \) の値を表に書き出していくと,
\( 1<\dfrac{b}{a}<4 \) となる組み合わせは7通り,すべての組み合わせは15通りなので,
求める確率は,\( \dfrac{7}{15} \)
|
Bの箱 |
| \( \fbox{1} \) |
\( \fbox{3} \) |
\( \fbox{5} \) |
\( \fbox{7} \) |
\( \fbox{9} \) |
| Aの箱 |
\( \fbox{1} \) |
\( 1 \) |
\( 3 \) |
\( 5 \) |
\( 7 \) |
\( 9 \) |
| \( \fbox{2} \) |
\( \dfrac{1}{2} \) |
\( \dfrac{3}{2} \) |
\( \dfrac{5}{2} \) |
\( \dfrac{7}{2} \) |
\( \dfrac{9}{2} \) |
| \( \fbox{3} \) |
\( \dfrac{1}{3} \) |
\( 1 \) |
\( \dfrac{5}{3} \) |
\( \dfrac{7}{3} \) |
\( 3 \) |
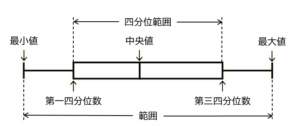
(6) ある中学校の剣道部,卓球部,水泳部の部員が反復横とびの測定を行った。 右図は,その記録を箱ひげ図に表したものである。次のア~オのうち,右図からわかることとして正しいものはどれですか。すべて選び,記号を ○ で囲みなさい。
ア 三つの部の部員のうち,記録が \( 60 \) 回以上の部員は1人だけである。
イ 剣道部の記録の四分位範囲と,水泳部の記録の四分位範囲は同じである。
ウ 三つの部のうち,記録の範囲が最も大きいのは卓球部である。
エ 第1四分位数が最も小さいのは,水泳部の記録である。
オ 卓球部では,半数以上の部員の記録が \( 55 \) 回以上である。
【解説】
ア 剣道部の最大値は \( 60 \) 回より大きく,卓球部の最大値は \( 60 \) 回なので,
記録が \( 60 \) 回以上の部員は少なくとも剣道部と卓球部に1人ずつはおり,あてはまらない。
イ 四分位範囲は,第3四分位数 \( – \) 第1四分位数 で求めることができるので,
剣道部 ・・・ \( 50-45=5 \)(回)
水泳部 ・・・ \( 50-45=5 \)(回)
ウ 範囲は,棒の部分の左端から右端までの長さで表されるので,もっとも大きいのは剣道部。
エ 第1四分位数は,箱の左端の値になるので,最も小さいのは,剣道部。
オ 箱の中の縦線は第二四分位数(中央値)を表しています。
卓球部の中央値は \( 55 \) 回より大きいので,半数以上の部員の記録が \( 55 \) 回以上であるといえます。
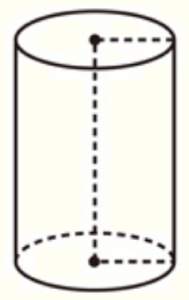
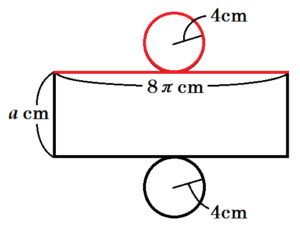
(7) 右図の立体は,底面の半径が \( 4 \; cm \),高さが \( a \; cm \) の円柱である。右図の円柱の表面積は \( 120\pi{} \; cm^2 \) である。 \( a \) の値を求めなさい。
【解説】
この円柱を展開すると,右の図のとおり,
半径 \( 4 \; cm \) の円2つと縦 \( a \; cm \),
横 \( 8\pi{} \; cm \) の長方形になります。
これらの面積の合計が \( 120\pi{} \; cm^2 \) なので,
\( \pi{} \times 4^2 \times 2+a \times 8\pi{}=120\pi{} \)
\( 32\pi{}+8\pi{}a=120\pi{} \)
\( 8\pi{}(4+a)=120\pi{} \)
\( 4+a=15 \)
\( a=11 \)
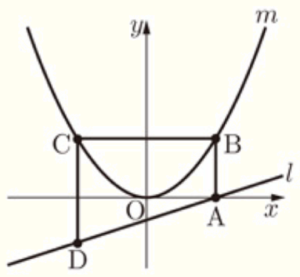
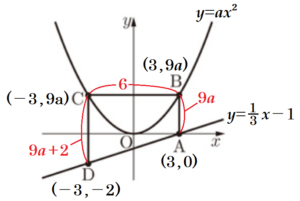
(8) 右図において,\( m \) は関数 \( y=ax^2 \) ( \( a \) は正の定数) のグラフを表し,\( l \) は関数 \( y=\dfrac{1}{3}x-1 \) のグラフを表す。\( A \) は,\( l \) と \( x \) 軸との交点である。\( B \) は,\( A \) を通り \( y \) 軸に平行な直線と \( m \) との交点である。\( C \) は,\( B \) を通り \( x \) 軸に平行な直線と \( m \) との交点のうち \( B \) と異なる点である。\( D \) は,\( C \) を通り \( y \) 軸に平行な直線と \( l \) との交点である。
四角形 \( ABCD \) の面積は \( 21 \; cm^2 \) である。\( a \) の値を求めなさい。答えを求める過程がわかるように,途中の式を含めた求め方も説明すること。ただし,原点 \( O \) から点 \( (1,0) \) までの距離,原点 \( O \) から点 \( (0,1) \) までの距離はそれぞれ \( 1 \; cm \) であるとする。
【解答】
\( A \) は,\( y=\dfrac{1}{3}x-1 \) と \( x \) 軸との交点なので,
\( A \) の座標は,\( A(3,0) \)
\( B \) は,\( y=ax^2 \) 上の点で,\( x \) 座標は \( 3 \) なので,
\( B \) の座標は,\( B(3,9a) \)
\( C \) は,\( y=ax^2 \) 上の点で,\( y \) 座標は \( 9a \) なので,
\( C \) の座標は,\( C(-3,9a) \)
\( D \) は,\( y=\dfrac{1}{3}x-1 \) 上の点で,\( x \) 座標は \( -3 \) なので,
\( D \) の座標は,\( D(-3,2) \)
以上より,\( AB=9a \; cm,CD=9a+2 \; cm,BC=6 \; cm \) であり,
四角形 \( ABCD \) は台形なので,面積の関係を方程式として解くと,
\( (9a+9a+2) \times 6 \times \dfrac{1}{2}=21 \)
\( 18a+2=7 \)
\( a=\dfrac{5}{18} \)
大問3
自宅で加湿器を利用しているDさんは,加湿器を使うと加湿器のタンクの水の量が一定の割合で減っていくことに興味をもち,「加湿器を使用した時間」と「タンクの水の量」との関係について考えることにした。
Dさんの自宅の加湿器は,強モード,弱モードのどちらかのモードを選んで使うことができる。タンクには水が \( 840 \; mL \) 入っており,強モードで使用する場合「タンクの水の量」は毎分 \( 6 \; mL \) の割合で減り,弱モードで使用する場合「タンクの水の量」は毎分 \( 2 \; mL \) の割合で減る。
次の問いに答えなさい。
(1) Dさんは,加湿器を強モードで使用する場合について考えた。
「加湿器を使用した時間」が \( x \) 分のときの「タンクの水の量」を \( y \; mL \) とする。また, \( 0≦x≦140 \) とし,\( x=0 \) のとき \( y=840 \) であるとする。
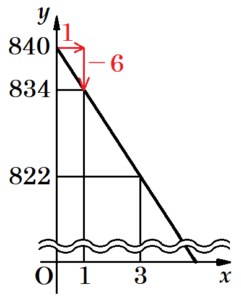
① 次の表は,\( x \) と \( y \) との関係を示した表の一部である。表中の(ア),(イ)に当てはまる数をそれぞれ書きなさい。

【解答】
(ア) ・・・ \( 822 \)
(イ) ・・・ \( 786 \)
【解説】
「タンクの水の量」は毎分 \( 6 \; mL \) の割合で減るので,
\( 3 \) 分で減る水の量の合計は \( 18 \; mL \) であり,\( y=840-18=822 \)
\( 9 \) 分で減る水の量の合計は \( 54 \; mL \) であり,\( y=840-54=786 \)
② \( y \) を \( x \) の式で表しなさい。
【解説】
\( 1 \) 分あたりに減る水の量(変化の割合)は \( 6 \; mL \) で
つねに一定なので,\( x \) と \( y \) との関係は一次関数の関係になります。
➀ の表からグラフを書いてみると,
\( x \) の値が \( 1 \) 増える間に \( y \) の値は \( 6 \) 減るので,
求める式を \( y=ax+b \) とすると,
傾き \( a=\dfrac{-6}{1}=-6 \),切片 \( b \) の値は \( 840 \)
よって,求める式は \( y=-6x+840 \)
➂ \( y=450 \) となるときの \( x \) の値を求めなさい。
【解説】
\( y=-6x+840 \) に \( y=450 \) を代入すると,
\( 450=-6x+840 \)
\( 6x=390 \)
\( x=65 \)
(2) Dさんは, タンクに水が \( 840 \; mL \) 入った状態から加湿器を使い始め,途中でモードを切りかえて使用した。
初めの「タンクの水の量」は \( 840 \; mL \) である。加湿器を最初は強モードで \( s \) 分間使用し,その後
続けて弱モードに切りかえて \( t \) 分間使用したところ,タンクの水はちょうどなくなった。 加湿器を強モードで使用した時間と弱モードで使用した時間の合計は \( 192 \) 分であった。\( s,t \) の値をそれぞれ求めなさい。 ただし,モードの切りかえにかかる時間はないものとする。
【解説】
「タンクの水の量」の関係と加湿器を使用した時間の関係を連立方程式として解くと,
\( \left\{ \begin{array}{}
6s+2t=840 \;\; ・・・ \;\; ➀ \\
s+t=192 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \div 2 \) すると,
\( 3s+t=420 \) ・・・ ➀’
➀’\( – \) ➁
\( 2s=228 \)
\( s=114 \)
➁ に代入すると,
\( 114+t=192 \)
\( t=78 \)
大問4
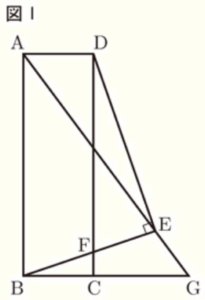
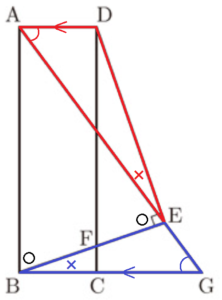
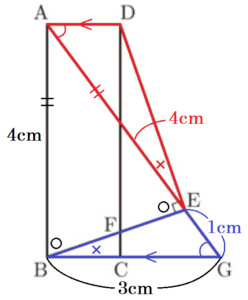
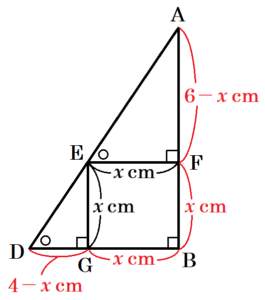
[I] 図Iにおいて,四角形 \( ABCD \) は長方形であり,\( AB>AD \) である。\( △ABE \) は \( AB=AE \) の二等辺三角形であり,\( E \) は直線 \( DC \) について \( B \) と反対側にある。\( D \) と \( E \) とを結んでできる線分 \( DE \) は,辺 \( BE \) に垂直である。\( F \) は,辺 \( BE \) と辺 \( DC \) との交点である。\( G \) は,直線 \( AE \) と直線 \( BC \) との交点である。
次の問いに答えなさい。
(1) \( △AED \) ∽ \( △GBE \) であることを証明しなさい。
【解答】
\( △AED \) と \( △GBE \) において,
長方形の向かい合う辺は平行なので,\( AD//BG \)
錯角は等しいので,
\( ∠EAD=∠BGE \) ・・・ ➀
仮定より,\( DE⊥BE \) なので,
\( ∠AEB+∠AED=90° \)
\( ∠AED=90°-∠AEB \) ・・・ ➁
長方形の内角はすべて \( 90° \) なので,
\( ∠ABE+∠GBE=90° \)
\( ∠GBE=90°-∠ABE \) ・・・ ➂
仮定より,\( △ABE \) は二等辺三角形で,
底角は等しいので,
\( ∠AEB=∠ABE \) ・・・ ➃
➁➂➃より,\( ∠AED=∠GBE \) ・・・ ➄
➀➄より,2組の角がそれぞれ等しいので,
\( △AED \) ∽ \( △GBE \)
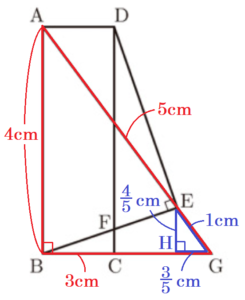
(2) \( AB=4 \; cm,BG=3 \; cm \) であるとき,
① 辺 \( AD \) の長さを求めなさい。
【解答】
\( \dfrac{4}{3} \; cm \)
【解説】
\( △AED \) において,三平方の定理より,
\( AG^2=AB^2+BG^2=4^2+3^2=25 \)
\( AG=5 \; (cm) \) ( \( AG>0 \) より)
\( AB=AE=4 \; cm \) なので,
\( GE=AG-AE=1 \; (cm) \)
(1)より,\( △AED \) ∽ \( △GBE \) なので,
\( EA:BG=AD:GE \)
\( 4:3=AD:1 \)
\( AD=\dfrac{4}{3} \; (cm) \)
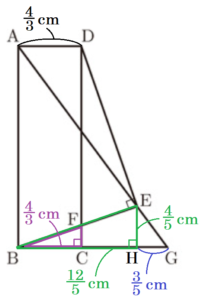
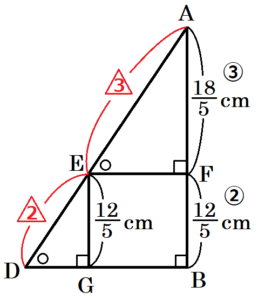
② 線分 \( FC \) の長さを求めなさい。
【解答】
\( \dfrac{4}{9} \; cm \)
【解説】
\( E \) から線分 \( BG \) に垂線をひき,交点を \( H \) とすると,
\( △ABG \) ∽ \( △EHG \) なので,
\( BG:HG=AG:EG \)
\( 3:HG=5:1 \)
\( HG=\dfrac{3}{5} \; (cm) \)
\( AB:EH=AG:EG \)
\( 4:EH=5:1 \)
\( EH=\dfrac{4}{5} \; (cm) \)
\( BG=3 \; cm,HG=\dfrac{3}{5} \; cm \) より,
\( BH=3-\dfrac{3}{5}=\dfrac{12}{5} \; (cm) \)
\( △BEH \) ∽ \( △EFC \) なので,
\( EH:FC=BH:BC \)
\( \dfrac{4}{5}:FC=\dfrac{12}{5}:\dfrac{4}{3} \)
\( 12:15FC=36:20 \)
\( 4:5FC=9:5 \)
\( 45FC=20 \)
\( FC=\dfrac{4}{9} \; (cm) \)
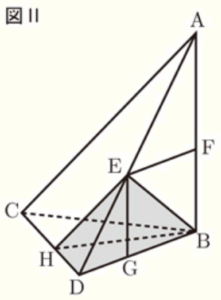
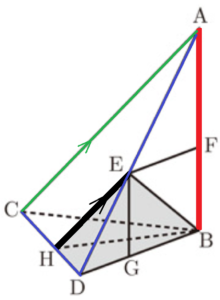
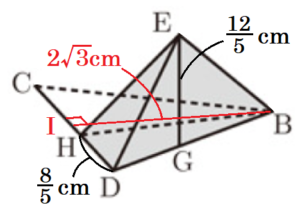
[Ⅱ] 図Ⅱにおいて,立体 \( A-BCD \) は三角すいであり,直線 \( AB \) は平面 \( BCD \) と垂直である。 \( △BCD \) は,1辺の長さが \( 4 \; cm \) の正三角形である。\( AB=6 \; cm \) である。\( E \) は,辺 \( AD \) 上にあって,\( A,D \) と異なる点である。\( E \) と \( B \) とを結ぶ。\( F \) は,\( E \) を通り辺 \( DB \) に平行な直線と辺 \( AB \) との交点である。\( G \) は,\( E \) を通り辺 \( AB \) に平行な直線と辺 \( DB \) との交点である。\( H \) は,\( E \) を通り辺 \( AC \) に平行な直線と辺 \( CD \) との交点である。\( H \) と \( B \) とを結ぶ。
次の問いに答えなさい。
(3) 次のア~エのうち,線分 \( EH \) とねじれの位置にある辺はどれですか。一つ選び,記号を ○ で囲みなさい。
ア 辺 \( AB \) イ 辺 \( AC \) ウ 辺 \( AD \) エ 辺 \( CD \)
【解説】
ねじれの位置にある直線はどこまでいっても交わらない2直線のうち,平行でないものをいいます。
ウ 辺 \( AD \) と エ 辺 \( CD \) は,それぞれ辺 \( EH \) と点 \( E,H \) で交わるので,あてはまりません。
イ 辺 \( AC \) は,辺 \( EH \) と交わりませんが,仮定より,\( AC//EH \) なので,あてはまりません。
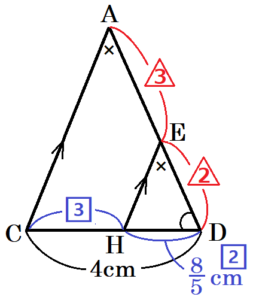
(4) \( EF=EG \) であるとき,
① 線分 \( EG \) の長さを求めなさい。
【解答】
\( \dfrac{12}{5} \; cm \)
【解説】
\( △AEF \) と \( △EDG \) は,
\( EF//DB \) より,\( ∠AEF=∠EDG \)
\( EF⊥AB,EG⊥DB \) より,
\( ∠AFE=∠EGD \)
であり,2組の角がそれぞれ等しいので,
\( △AEF \) ∽ \( △EDG \)
\( EF⊥AB,EG⊥DB,EF=EG \) より,
四角形 \( EFBG \) は,
すべての内角が \( 90° \) で,となりあう2辺が等しいので正方形になっています。
\( EF=EG=x \; cm \) とすると,\( AB=6 \; cm,BD=4 \; cm \) より,
\( AF=6-x \; cm,DG=4-x \; cm \) と
表すことができるので,
\( AF:EG=EF:DG \)
\( (6-x):x=x:(4-x) \)
\( (6-x)(4-x)=x^2 \)
\( x^2-10x+24=x^2 \)
\( 10x=24 \)
\( x=\dfrac{12}{5} \; (cm) \)
② 立体 \( EHDB \) の体積を求めなさい。
【解答】
\( \dfrac{32 \sqrt{3}}{25} \; cm^3 \)
【解説】
\( AB=6 \; cm,FB=EG=\dfrac{12}{5} \; cm \) より,
\( AF=6-\dfrac{12}{5}=\dfrac{18}{5} \; (cm) \)
\( △AEF \) ∽ \( △ADB \) より,
\( AE:ED=AF:FB=\dfrac{18}{5}:\dfrac{12}{5}=3:2 \)
\( △DEH \) と \( △DAC \) は,
\( ∠D \) は共通
\( EH//AC \) より,\( ∠DEH=∠DAC \)
であり,2組の角がそれぞれ等しいので,
\( △DEH \) ∽ \( △DAC \)
対応する辺の比は等しいので,
\( CH:HD=AE:ED=3:2 \)
\( CD=4 \; cm \) より,
\( HD=\dfrac{2}{5}CD=\dfrac{8}{5} \; (cm) \)
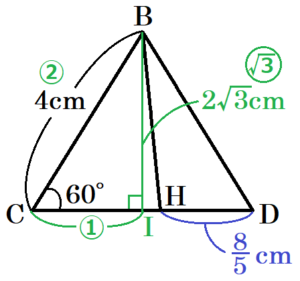
\( △BCD \) において,
\( B \) から辺 \( CD \) に垂線をひき,交点を \( I \) とすると,
\( △BCI \) は \( 30°,60°,90° \) の直角三角形なので,
\( BI=\dfrac{\sqrt{3}}{2}BC=2\sqrt{3} \; (cm) \)
立体 \( EHDB \) は \( △BDH \) を底面,線分 \( EG \) を高さとする三角すいなので,その体積を \( V \) とすると,
\( V=\left( DH \times BI \times \dfrac{1}{2} \right) \times EG \times \dfrac{1}{3} \)
\( =\left( \dfrac{8}{5} \times 2\sqrt{3} \times \dfrac{1}{2} \right) \times \dfrac{12}{5} \times \dfrac{1}{3} \)
\( =\dfrac{32 \sqrt{3}}{25} \; (cm^3) \)