大問1
(1) \( 10xy^2 \times (-\dfrac{2}{3}xy)^2 \div (-5y^2) \) を計算しなさい。
【解答】
\( -\dfrac{8}{9}x^3y^2 \)
【解説】
\( =10xy^2 \times \dfrac{4}{9}x^2y^2 \div (-5y^2) \)
\( =\dfrac{10xy^2 \times 4x^2y^2}{9 \times (-5y^2)} \)
\( =-\dfrac{8}{9}x^3y^2 \)
(2) \( x=3+\sqrt{7},y=3-\sqrt{7} \) のとき,\( x^3y-xy^3 \) の値を求めなさい。
【解説】
\( x^3y-xy^3=xy(x^2-y^2) \)
\( =xy(x+y)(x-y) \)
\( x=3+\sqrt{7},y=3-\sqrt{7} \) より,
\( xy=(3+\sqrt{7})(3-\sqrt{7})=9-7=2 \)
\( x+y=(3+\sqrt{7})+(3-\sqrt{7})=6 \)
\( x-y=(3+\sqrt{7})-(3-\sqrt{7})=2\sqrt{7} \)
を代入すると,
\( xy(x+y)(x-y)=2 \times 6 \times 2\sqrt{7}=24\sqrt{7} \)
(3) 2次方程式 \( (5x-2)^2-2(5x-2)-3=0 \) を解きなさい。
【解答】
\( x=\dfrac{1}{5},1 \)
【解説】
\( 5x-2=A \) とすると,
\( (5x-2)^2-2(5x-2)-3=0 \)
\( A^2-2A-3=0 \)
\( (A+1)(A-3)=0 \)
\( A=-1,3 \)
\( A=-1 \) のとき,
\( 5x-2=-1 \)
\( 5x=1 \)
\( x=\dfrac{1}{5} \)
\( A=3 \) のとき,
\( 5x-2=3 \)
\( 5x=5 \)
\( x=1 \)
(4) 次のア~エの調査は,全数調査と標本調査のどちらでおこなわれますか。標本調査でおこなわれるものを二つ選び,その記号を書きなさい。
ア ある河川の水質調査
イ ある学校でおこなう健康診断
ウ テレビ番組の視聴率調査
エ 日本の人口を調べる国勢調査
【解説】
全数調査では,対象となるものをもれなく「すべて」調査し,
標本調査では,対象となるものから「一部」を抜き出し調査します。
ア ある河川の水質調査 ・・・ 「一部」の水を取り出して調査するので,標本調査
イ ある学校でおこなう健康診断 ・・・ 全員が受けるので,全数検査
ウ テレビ番組の視聴率調査 ・・・ 一部の人だけを調査しているので,標本調査
エ 日本の人口を調べる国勢調査 ・・・ 全員が調査されるので,全数調査
(5) 100円硬貨1枚と,50円硬貨2枚を同時に投げるとき,表が出た硬貨の合計金額が100円以上になる確率を求めなさい。
ただし,硬貨の表と裏の出かたは,同様に確からしいものとします。
【解説】
50円硬貨2枚に「50円A」,「50円B」と名前をつけ,
それぞれの表裏の組み合わせを樹形図で書き出すと,
表が出た硬貨の合計金額が100円以上になる組み合わせは5通り,
すべての組み合わせは8通りなので,
求める確率は \( \dfrac{5}{8} \)

(6) 半径 \( 7 \; cm \) の球を,中心から \( 4 \; cm \) の距離にある平面で切ったとき,切り口の円の面積を求めなさい。
【解答】
\( 33\pi{} \; cm^2 \)
【解説】
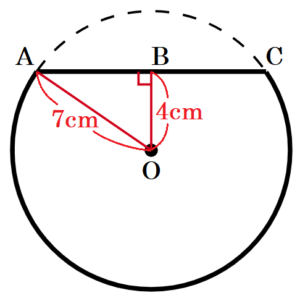
できる立体をさらに中心を通り垂直な平面で切った図を考えると,
右の図のようになります。
線分 \( OA \) は球の半径なので,\( OA=7 \; cm \)
仮定より,\( OB=4 \; cm \)
\( △OAB \) において,三平方の定理より,
\( AB^2=OA^2-OB^2 \)
\( =7^2-4^2 \)
\( =33 \)
\( AB=\sqrt{33} \; (cm) \)
よって,切り口の円は半径 \( \sqrt{33} \; cm \) なので,その面積は,
\( \pi{} \times \sqrt{33}^2=33\pi{} \; (cm^2) \)
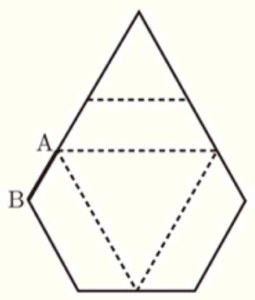
(7) 右の図はある立体の展開図で,これを組み立ててつくった立体は,3つの合同な台形と2つの相似な正三角形が面になります。
この立体を \( V \) とするとき,立体 \( V \) の頂点と辺の数をそれぞれ求めなさい。また,立体 \( V \) の辺のうち,辺 \( AB \) とねじれの位置になる辺の数を求めなさい。
【解答】
頂点の数 ・・・ \( 6 \) 個
辺の数 ・・・ \( 9 \) 本
ねじれの辺の数 ・・・ \( 2 \) 本
【解説】
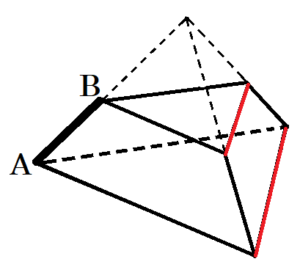
組み立ててできる立体は,右の図のような三角すいの上側を
切り取った形になります。
よって,頂点の数は6個,辺の数は9本になります。
また,辺 \( AB \) とねじれの位置になる辺は赤の辺2本になります。
(8) ある3桁の自然数 \( X \) があり,各位の数の和は \( 15 \) です。また,\( X \) の百の位の数と一の位の数を入れかえてつくった数を \( Y \) とすると,\( X \) から \( Y \) を引いた値は \( 396 \) でした。十の位の数が \( 7 \) のとき,\( X \) を求めなさい。
【解説】
\( X \) の百の位の数を \( a \),一の位の数を \( b \) (\( a,b \) は整数)とすると,
各位の数の和は \( 15 \) なので,\( a+7+b=15 \),つまり,\( a+b=8 \) ・・・ ➀ と表すことができます。
また,\( X=100a+70+b,Y=100b+70+a \) と表すことができるので,
\( X-Y=(100a+70+b)-(100b+70+a) \)
\( 396=99a-99b \)
\( a-b=4 \) ・・・ ➁
となります。
➀➁を連立方程式として解くと,
\( \left\{ \begin{array}{}
a+b=8 \;\; ・・・ \;\; ➀ \\
a-b=4 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀+➁
\( 2a=12 \)
\( a=6 \)
➀に代入
\( 6+b=8 \)
\( b=2 \)
よって,\( X \) は \( 672 \) になります。
(9) 関数 \( y=2x^2 \) について, \( x \) の変域が \( a≦x≦a+4 \) のとき,\( y \) の変域は \( 0≦y≦18 \) となりました。このとき,\( a \) の値を求めなさい。
【解説】
二次関数 \( y=ax^2 \; (a>0) \) において,
\( y \) の最小値が \( 0 \) であるとき,\( x \) の変域は \( 0 \) を含むので,\( -4≦a≦0 \) とわかります。
\( x=a \) のとき,\( y \) が最大値 \( 18 \) になるとすると,
\( y=2x^2 \)
\( 18=2 \times a^2 \)
\( 2a^2=18 \)
\( a^2=9 \)
\( a=±3 \)
\( -4≦a≦0 \) より,あてはまるのは \( a=-3 \)
\( x=a+4 \) のとき,\( y \) が最大値 \( 18 \) になるとすると,
\( y=2x^2 \)
\( 18=2 \times (a+4)^2 \)
\( (a+4)^2=9 \)
\( a+4=±3 \)
\( a=-1,-7 \)
\( -4≦a≦0 \) より,あてはまるのは \( a=-1 \)
以上より,\( a=-3,-1 \)
(10) 次の図は,18人の生徒の通学時間をヒストグラムに表したものです。このヒストグラムでは,通学時間が \( 10 \) 分以上 \( 20 \) 分未満の生徒の人数は2人であることを表しています。
下の箱ひげ図は,このヒストグラムに対応するものではないと判断できます。その理由を,ヒストグラムの階級にふれながら説明しなさい。
【解答】
ヒストグラムでは,第3四分位数は \( 40 \) 分以上 \( 50 \) 分未満の階級に含まれているが,
箱ひげ図では,第3四分位数は \( 50 \) 分以上 \( 60 \) 分未満となっており,異なっている。
【解説】
全体で18人なので,
第1四分位数になるのは通学時間が短い方から5番目の人の値
第3四分位数になるのは通学時間が長い方から5番目の人の値
になります。
大問2
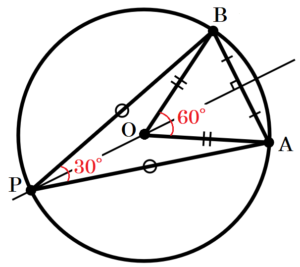
(1) 下の図の点 \( A \) は,北の夜空にみえる,ある星の位置を表しています。2時間後に観察すると,その星は点 \( B \) の位置にありました。北の夜空の星は北極星を回転の中心として1時間に \( 15° \) だけ反時計回りに回転移動するものとしたときの北極星の位置を点 \( P \) とします。このとき,点 \( P \) をコンパスと定規を使って作図しなさい。
ただし,作図するためにかいた線は,消さないでおきなさい。
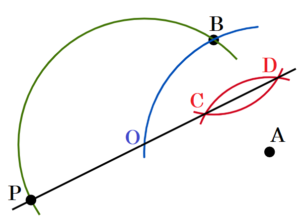
【解答】
手順1 点 \( A,B \) を中心に円弧を描く
(交点を点 \( C,D \) とします。)
手順2 直線 \( CD \) を描く
手順3 点 \( A \) を中心に半径 \( AB \) となる円弧を描く
(直線 \( CD \) との交点を点 \( O \) とします。)
手順4 点 \( O \) を中心に半径 \( OB \) となる円弧を描く
直線 \( CD \) と手順4の円弧の交点が求める点 \( P \) になります。
【解説】
点 \( B \) は,点 \( P \) を中心に点 \( A \) が回転移動した
ものなので,\( AP=BP \) になります。
ここから,\( △ABP \) は二等辺三角形なので,
点 \( P \) は,「線分 \( AB \) の垂直二等分線上の点」
になります。
また,
\( 1 \) 時間に \( 15° \) だけ回転移動するということは,
\( 2 \) 時間では \( 30° \) 回転移動するので,\( ∠APB=30° \) になります。
ここで,線分 \( AB \) を1辺とする正三角形 \( OAB \) を考えると,
点 \( O \) も「線分 \( AB \) の垂直二等分線上の点」に
なります。
\( △ABP \) と \( △OAB \) は,線分 \( AB \) が共通で,
\( ∠APB=30°,∠AOB=60° \)
なので,\( ∠AOB=2∠APB \) であり,
\( ∠APB \) は円 \( O \) の円周角,
\( ∠AOB \) は円 \( O \) の中心角
となります。
ここから,\( OP=OB \) になります。
よって,点 \( P \) は「線分 \( AB \) の垂直二等分線上の点」かつ「\( OP=OB \) となる点」になります。
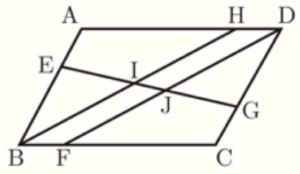
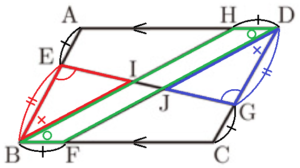
(2) 下の図のように,平行四辺形 \( ABCD \) の辺 \( AB,BC,CD,DA \) 上に4点 \( E,F,G,H \) をそれぞれとり,線分 \( EG \) と \( BH \),\( DF \) との交点をそれぞれ \( I,J \) とします。
\( AE=BF=CG=DH \) のとき,\( △BEI≡△DGJ \) であることを証明しなさい。
【解答】
\( △BEI \) と \( △DGJ \) において,
\( BE=AB-AE \)
\( DG=CD-CG \)
平行四辺形の向かい合う辺の長さは等しいので,
\( AB=CD \)
仮定より,\( AE=CG \)
ここから,\( BE=DG \) ・・・ ➀
平行四辺形の向かい合う辺は平行なので,\( AB//CD \)
錯角は等しいので,\( ∠BEI=∠DGJ \) ・・・ ➁
\( ∠EBI=∠ABC-∠FBH \) ・・・ ➂
\( ∠GDJ=∠CDA-∠HDF \) ・・・ ➃
平行四辺形の向かい合う角は等しいので,
\( ∠ABC=∠CDA \) ・・・ ➄
平行四辺形の向かい合う辺は平行なので,\( BC//AD \)
仮定より,\( BF=DH \)
ここから,向かい合う辺が平行で長さが等しいので,
四角形 \( BFDH \) は平行四辺形である。
平行四辺形の向かい合う角は等しいので,
\( ∠FBH=∠HDF \) ・・・ ⑥
➂➃➄➅より,\( ∠EBI=∠GDJ \) ・・・ ➆
①➁➆より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △BEI≡△DGJ \)
大問3
次は,先生とAさん,Bさんの会話です。これを読んで,あとの各問に答えなさい。
先生 「次の表は,\( 2 \) 以上の自然数 \( n \) について,その逆数 \( \dfrac{1}{n} \) の値を小数で表したものです。
これをみて,気づいたことを話し合ってみましょう。」

Aさん 「\( n \) の値によって,割り切れずに限りなく続く無限小数になるときと,割り切れて終わりのある
有限小数になるときがあるね。」
Bさん 「なにか法則はあるのかな。」
Aさん 「この表では,\( n \) が偶数のときは,有限小数になることが多いね。」
Bさん 「だけど,この表の中の偶数でも,\( n= \) ア のときは無限小数になっているよ。」
Aさん 「それでは,\( n \) が奇数のときは,無限小数になるのかな。」
Bさん 「\( n \) が \( 5 \) のときは,有限小数になっているね。\( n \) が2桁の奇数のときは,\( \dfrac{1}{n} \) は無限小数に
なるんじゃないかな。」
Aさん 「それにも,\( n= \) イ という反例があるよ。」
Bさん 「有限小数になるのは, \( 2,4,5,8,10,16,20 \), イ , \( 32 \),・・・ 」
Aさん 「それぞれ素因数分解してみると,なにか法則がみつかりそうだね。」
先生 「いいところに気づきましたね。他にも,有理数を小数で表すと,有限小数か循環小数になることを
学習しましたね。」
Bさん 「循環小数とは,同じ数字が繰り返しあらわれる無限小数のことですね。」
Aさん 「その性質を利用すれば,循環小数の小数第30位の数なども求めることができますね。」
(1) ア , イ にあてはまる数を求めなさい。
【解答】
ア ・・・ \( 6 \)
イ ・・・ \( 25 \)
(2) \( \dfrac{1}{7} \) の値を小数で表したときの小数第30位の数を求めなさい。また,小数第1位から小数第30位までの各位の数の和を求めなさい。
【解答】
小数第30位の数 ・・・ \( 7 \)
小数第30位までの各位の数の和 ・・・ \( 135 \)
【解説】
表から,小数第1位以降,「\( 142857 \)」が順番に繰り返されているので,
小数第○位の ○ の値が \( 6 \) の倍数になるところの数字は \( 7 \) になります。
よって,小数第30位の数字は \( 7 \) になります。
小数第30位までに「\( 142857 \)」を5回繰り返すので,その和は,
\( (1+4+2+8+5+7) \times 5=27 \times 5=135 \)
大問4
次の図は,コンピュータソフトを使って,座標平面上に関数 \( y=ax^2 \) のグラフと,一次関数 \( y=bx+c \) のグラフを表示したものです。\( a,b,c \) の数値を変化させたときの様子について,下の各問に答えなさい。
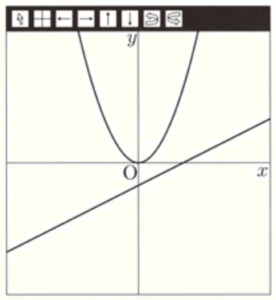
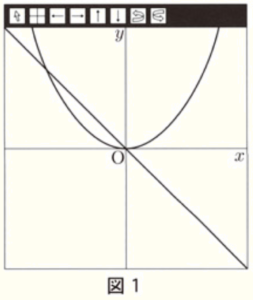
(1) グラフが右の図1のようになるとき,\( a,b,c \) の大小関係を,不等号を使って表しなさい。
【解説】
図1より,
\( y=ax^2 \) の曲線は下に凸なので,\( a>0 \)
\( y=y=bx+c \) の直線は右下がりなので,\( b<0 \)
また,原点 \( O \) を通っているので,\( c=0 \)
よって,\( b<c<a \)
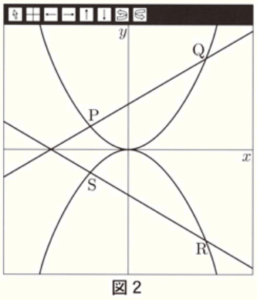
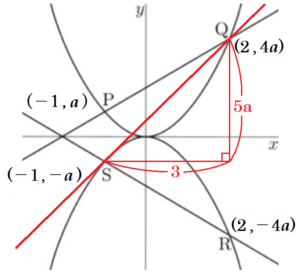
(2) 右の図2は,\( a,b,c \) がすべて正のときの,関数 \( y=ax^2 \) と \( y=-ax^2 \) のグラフと,一次関数 \( y=bx+c \) と \( y=-bx-c \) のグラフを表示したものです。
図2のように,\( y=ax^2 \) と \( y=bx+c \) とのグラフの交点を \( P,Q \) とし,\( y=-ax^2 \) と \( y=-bx-c \) とのグラフの交点を \( S,R \) とすると,四角形 \( PQRS \) は台形になります。
このとき,次の ➀,➁ に答えなさい。
➀ \( a,b \) の値を変えないまま,\( c \) の値を大きくすると,台形 \( PQRS \) の面積はどのように変化するか,
次のア~ウの中から一つ選び,その記号を書きなさい。また,その理由を説明しなさい。
ア 大きくなる イ 一定である ウ 小さくなる
【解答】
ア
\( c \) の値を大きくすると,\( PS,QR \) の長さはともに長くなる。
また,線分 \( PS,QR \) と \( x \) 軸の交点をそれぞれ \( T,U \) とすると,
\( TU \) の長さも長くなる。
台形 \( PQRS \) の面積は,\( (PS+QR) \times TU \times \dfrac{1}{2} \) で求められるので,
\( PS,QR,TU \) がすべて長くなると,面積は大きくなる。
➁ 点 \( P,Q \) の \( x \) 座標がそれぞれ \( -1,2 \) で,直線 \( QS \) の傾きが \( 1 \) のとき,\( a,b,c \) の値を求めなさい。また,そのときの台形 \( PQRS \) を \( x \) 軸を軸として1回転させてできる立体の体積を求めなさい。
ただし,座標軸の単位の長さを \( 1 \; cm \) とします。
【解答】
\( a=\dfrac{3}{5} \),\( b=\dfrac{3}{5} \),\( c=\dfrac{6}{5} \)
【解説】
【\( a,b,c \) の値】
\( P,Q,R,S \) の座標は,それぞれ
\( P(-1,a),Q(2,4a),R(2,-4a),S(-1,-a) \) と表せるので,直線 \( QS \) の傾きは,
\( \dfrac{4a-(-a)}{2-(-1)}=1 \)
\( \dfrac{5}{3}a=1 \)
\( a=\dfrac{3}{5} \)
\( a=\dfrac{3}{5} \) のとき,
\( P \left(-1,\dfrac{3}{5} \right),Q \left(2,\dfrac{12}{5} \right) \) なので,
直線 \( PQ \) の傾きは,
傾き \( b=\dfrac{\dfrac{12}{5}-\dfrac{3}{5}}{2-(-1)}=\dfrac{3}{5} \)
\( y=\dfrac{3}{5}x+c \) に \( x=-1,y=\dfrac{3}{5} \) を代入すると,
\( \dfrac{3}{5}=\dfrac{3}{5} \times (-1)+c \)
\( c=\dfrac{6}{5} \)
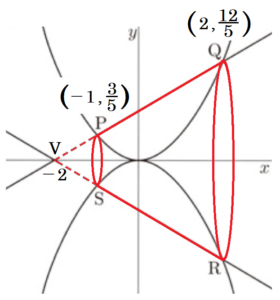
【立体の体積】
直線 \( PQ \) と \( x \) 軸の交点を点 \( V \) とすると,
直線 \( PQ \) の式は \( y=\dfrac{3}{5}x+\dfrac{6}{5} \) なので,
点 \( V \) の \( x \) 座標は,
\( 0=\dfrac{3}{5}x+\dfrac{6}{5} \)
\( x=−2 \)
よって,
求める立体は,
底面の半径 \( \dfrac{12}{5} \),高さ \( 4 \) の大きい円すいから,
底面の半径 \( \dfrac{3}{5} \),高さ \( 1 \) の小さい円すいを
切り取ったものになります。
大きい円すいの体積 \( =\pi{} \times \left( \dfrac{12}{5} \right)^2 \times 4 \times \dfrac{1}{3} \)
\( =\dfrac{192}{25}\pi{} \; (cm^3) \)
小さい円すいの体積 \( =\pi{} \times \left( \dfrac{3}{5} \right)^2 \times 1 \times \dfrac{1}{3} \)
\( =\dfrac{3}{25}\pi{} \; (cm^3) \)
求める円すいの体積 \( =\dfrac{192}{25}\pi{}-\dfrac{3}{25}\pi{}=\dfrac{189}{25}\pi{} \; (cm^3) \)
大問5
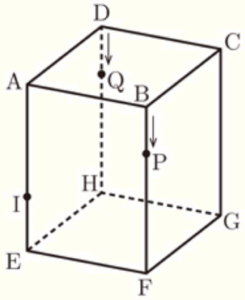
右の図のような,1辺の長さが \( 4 \; cm \) の正方形を底面とし,高さが \( 6 \; cm \) の直方体 \( ABCD-EFGH \) があり,辺 \( AE \) 上に \( AI=4 \; cm \) となる点 \( I \) をとります。
点 \( P \) が頂点 \( B \) を出発して毎秒 \( 1 \; cm \) の速さで辺 \( BF \) 上を頂点 \( F \) まで,点 \( Q \) は頂点 \( D \) を出発して毎秒 \( 1 \; cm \) の速さで辺 \( DH \) 上を頂点 \( H \) まで動きます。
点 \( P,Q \) がそれぞれ頂点 \( B,D \) を同時に出発するとき,次の各問に答えなさい。
(1) \( IP+PG \) の長さが最も短くなるのは,点 \( P \) が頂点 \( B \) を出発してから何秒後か求めなさい。
【解説】
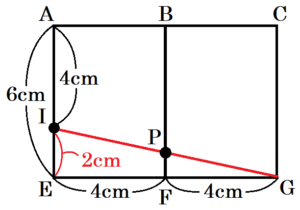
面 \( ABFE \) と面 \( BCGF \) に注目し,展開すると,
\( IP+PG \) の長さが最も短くなるとき,
3点 \( I,P,G \) が一直線上に並びます。
このとき,\( △GPF \) ∽ \( △GIE \) で,
点 \( F \) は線分 \( GE \) の中点なので,
\( PF:IE=GF:GE \)
\( PF:2=1:2 \)
\( PF=1 \; (cm) \)
よって,\( BP=6-1=5 \; (cm) \) であり,
点 \( P \) は毎秒 \( 1 \; cm \) の速さで動くので,求める時間は \( 5 \) 秒後になります。
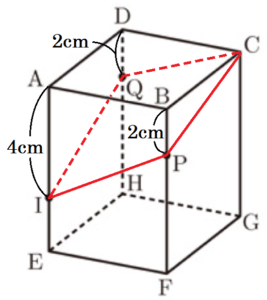
(2) 点 \( P,Q \) が頂点 \( B,D \) を同時に出発してから2秒後の3点 \( I,P,Q \) を通る平面で,直方体を切ります。このときにできる2つの立体のうち,頂点 \( A \) を含む立体の体積を,途中の説明も書いて求めなさい。
【解答】
出発してから2秒後の3点 \( I,P,Q \) を通る平面は頂点 \( C \) を通る。
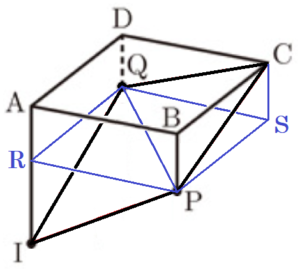
2点 \( P,Q \) を通り,面 \( ABCD \) と平行な面と
辺 \( AE \) の交点を点 \( R \),辺 \( CG \) の交点を点 \( S \) とすると,
三角すい \( I-PQR \) と三角すい \( C-PQS \) は,
どちらも底面が正方形 \( PSQR \) の半分,高さが \( 2 \; cm \) なので,体積は等しい。
よって,求める立体の体積は直方体 \( ABCD-PSQR \) の体積と等しいので,
\( 4 \times 4 \times 2=32 \; (cm^3) \)
【解説】
出発してから2秒後の線分 \( BP,DQ \) の長さは,
\( BP=DQ=2 \; cm\) なので,
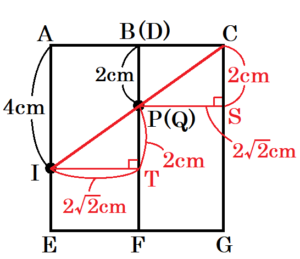
面 \( AEGC \) を正面になるようこの直方体を見ると
下の図のようになります。
点 \( I \) から辺 \( BF \) に垂線をひいた交点を \( T \),
点 \( P \) から辺 \( CG \) に垂線をひいた交点を \( S \)
とすると,\( △PIT≡△CPS \) となるので,
3点 \( I,P,Q \) を通る平面は,点 \( C \) を通ります。
頂点 \( A \) を含む方の立体について,
辺 \( AE \) 上に \( AR=2 \; cm \) となる点 \( R \) をとると,
面 \( PSQR \) に対して
突き出ている部分(三角すい \( I-PQR \) )と
欠けている部分(三角すい \( C-PQS \) )は,
どちらも底面が正方形 \( PSQR \) の半分,高さが \( 2 \; cm \) なので,体積は等しくなります。
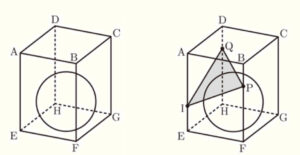
(3) 右の図のように,底面 \( EFGH \) に接するように半径 \( 2 \; cm \) の球を直方体の内部に置きます。
点 \( P,Q \) が頂点 \( B,D \) を同時に出発してから \( x \) 秒後の \( △IPQ \) は,球とちょうど1点で接しました。このときの \( x \) の値を求めなさい。
【解説】
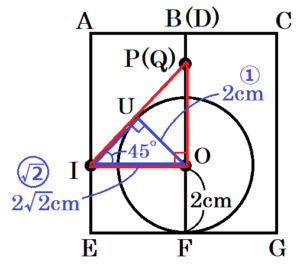
面 \( AEGC \) を正面になるようこの直方体を見ると,
出発してから \( x \) 秒後には右の図のようになります。
ここで,
\( △IPQ \) と球の接点を点 \( U \),
球の中心を点 \( O \)
とすると,
\( OU:IO=2:2\sqrt{2}=1:\sqrt{2} \)
\( ∠OUI=90° \)
より,
\( △IOU \) は直角二等辺三角形になっています。
球は,底面 \( EFGH \) に接していることから,
線分 \( OF=2 \; cm \),\( IO//EG \) なので,
\( △IOP \) も直角二等辺三角形になります。
ここから,
\( OP=IO=2\sqrt{2} \; cm \) であり,
\( BP=4-2\sqrt{2} \; cm \) となります。
点 \( P \) は毎秒 \( 1 \; cm \) の速さで動くので,
\( BP=4-2\sqrt{2} \; cm \) となるのは,\( x=4-2\sqrt{2} \) 秒後になります。







-アイキャッチ-120x68.jpg)