大問１
〔問１〕 \( -8+6^2 \div 9 \) を計算せよ。
〔問２〕 \( \dfrac{7a+b}{5}-\dfrac{4a-b}{3} \) を計算せよ。
〔問３〕 \( (\sqrt{6}-1) (2\sqrt{6}+9) \) を計算せよ。
〔問４〕 一次方程式 \( 4(x+8)=7x+5 \) を解け。
〔問５〕 連立方程式 \( \left\{ \begin{array}{}
2x+3y=1 \\
8x+9y=7 \\
\end{array} \right. \) を解け。
〔問６〕 二次方程式 \( 2x^2-3x-6=0 \) を解け。
〔問７〕 次の \( \fbox{あ}，\fbox{い} \) に当てはまる数字をそれぞれ答えよ。
この袋の中から同時に２個の玉を取り出すとき，２個とも青玉である確率は， \( \dfrac{\;\;\fbox{あ}\;\;}{\;\;\fbox{い}\;\;} \) である。
ただし，どの玉が取り出されることも同様に確からしいものとする。
２個とも青玉である組み合わせのところに ○ をつけてみます。
このとき，２個とも青玉である組み合わせは６通り，すべての組み合わせは１５通りなので，
求める確率は，\( \dfrac{6}{15}=\dfrac{2}{5} \)
〔問８〕 次の \( \fbox{うえ} \) に当てはまる数字をそれぞれ答えよ。
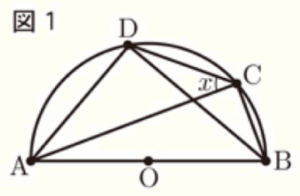
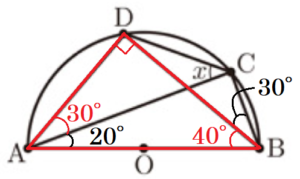
右の図１で，点 \( O \) は，線分 \( AB \) を直径とする半円の中心である。
点 \( C \) は, 弧 \( AB \) 上にある点で，点 \( A \)，点 \( B \) のいずれにも一致しない。
点 \( D \) は, 弧 \( AC \) 上にある点で，点 \( A \)，点 \( C \) のいずれにも一致しない。
点 \( A \) と点 \( C \)，点 \( A \) と点 \( D \)，点 \( B \) と点 \( C \)，点 \( B \) と点 \( D \)，
点 \( C \) と点 \( D \) をそれぞれ結ぶ。
\( ∠BAC=20°，∠CBD=30° \) のとき，\( x \) で示した \( ∠ACD \) の大きさは，\( \fbox{うえ} \) 度である。
ともに弧 \( CD \) に対する円周角なので，
\( ∠CAD=∠CBD=30° \)
直径に対する円周角なので，
\( ∠ADB=90° \)
三角形の内角の和は \( 180° \) なので，
\( ∠ABD=180°-(90°+50°)=40° \)
ともに弧 \( AD \) に対する円周角なので，
\( ∠ACD=∠ABD=40° \)
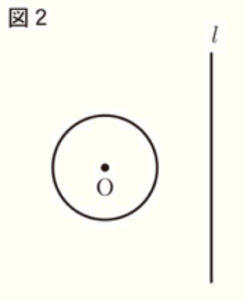
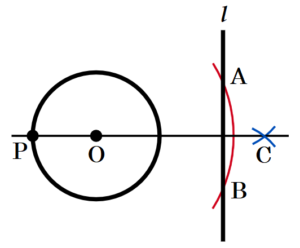
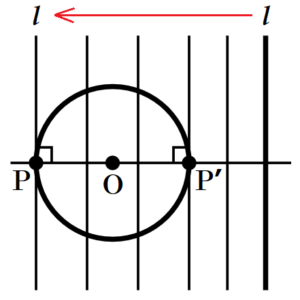
〔問９〕 右の図２で，円 \( O \) と直線 \( l \) は交わっていない。解答欄に示した図をもとにして，円 \( O \) の周上にあり，直線 \( l \) との距離が最も長くなる点 \( P \) を，定規とコンパスを用いて作図によって求め，
点 \( P \) の位置を示す文字Pも書け。
ただし，作図に用いた線は消さないでおくこと。
手順１ 点 \( O \) を中心に円弧を描く
(直線 \( l \) との交点を \( A，B \) とします)
手順２ 点 \( A，B \) を中心に円弧を描く
(交点を \( C \) とします)
手順３ ２点 \( O，C \) を通る直線を描く
手順３の直線と円 \( O \) の交点のうち，
直線 \( l \) から遠い方が求める点 \( P \) になります。
直線 \( l \) を円 \( O \) に近づける方向に動かしていくと，
直線 \( l \) が円 \( O \) の接線になるときの接点 \( P’ \) で
初めて直線 \( l \) と円 \( O \) が接触します。
さらに直線 \( l \) を動かしていくと，
最後に直線 \( l \) と円 \( O \) が接触する点 \( P \) は，
直線 \( l \) が円 \( O \) の接線になるときの接点になります。
円の中心を通る直線と接線は，接点において垂直に交わるので，
「点 \( O \) を通り，直線 \( l \) と垂直な直線」と円 \( O \) の交点のうち，
直線 \( l \) から遠い方が求める点 \( P \) になります。
大問２
Ｓさんのクラスでは，先生が示した問題をみんなで考えた。
次の各問に答えよ。
【先生が示した問題】
\( a，b \) を正の数とし，\( a>b \) とする。
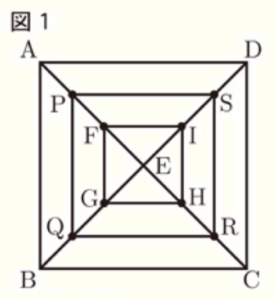
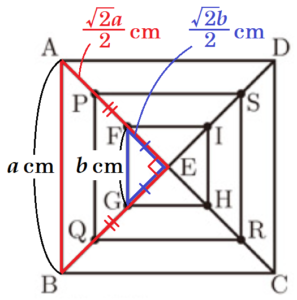
右の図１で，四角形 \( ABCD \) は，１辺の長さが \( a \; cm \) の正方形である。頂点 \( A \) と頂点 \( C \)，頂点 \( B \) と頂点 \( D \) をそれぞれ結び，線分 \( AC \) と線分 \( BD \) との交点を \( E \) とする。
線分 \( AE \) 上にあり，頂点 \( A \)，点 \( E \) のいずれにも一致しない点を \( F \) とする。
線分 \( BE \)，線分 \( CE \)，線分 \( DE \) 上にあり，\( EF=EG=EH=EI \) となる点をそれぞれ \( G，H，I \) とし，点 \( F \) と点 \( G \)，点 \( F \) と点 \( I \)，点 \( G \) と点 \( H \)，点 \( H \) と点 \( I \) をそれぞれ結ぶ。
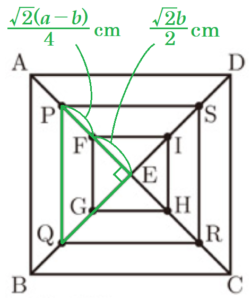
線分 \( AF \)，線分 \( BG \)，線分 \( CH \)，線分 \( DI \) の中点をそれぞれ \( P，Q，R，S \) とし，点 \( P \) と点 \( Q \)，点 \( P \) と点 \( S \)，点 \( Q \) と点 \( R \)，点 \( R \) と点 \( S \) をそれぞれ結ぶ。
線分 \( FG \) の長さを \( b \; cm \)，四角形 \( PQRS \) の周の長さを \( l \; cm \) とするとき，\( l \) を \( a，b \) を用いた式で表しなさい。
〔問１〕 【先生が示した問題】で，\( l \) の値を \( a，b \) を用いて \( l= \) \( cm \) と
表すとき， に当てはまる式を，次のア～エのうちから選び，記号で答えよ。
ア \( 2a+2b \) イ \( \dfrac{a+b}{2} \) ウ \( \dfrac{a-b}{2} \) エ \( 2a-2b \)
\( △ABE \) は直角二等辺三角形になっています。
また，同様の考え方で，\( EF=EG=EH=EI \) より，四角形 \( FGHI \) は正方形であり，
\( △FGE \) は直角二等辺三角形になっています。
\( △ABE \) は直角二等辺三角形なので，
\( AB：AE=\sqrt{2}：1 \) であり，
\( AE=\dfrac{AB}{\sqrt{2}}=\dfrac{a}{\sqrt{2}}=\dfrac{\sqrt{2}a}{2} \; (cm) \)
また，\( △FGE \) は直角二等辺三角形なので，
\( FG：FE=\sqrt{2}：1 \) であり，
\( FE=\dfrac{FG}{\sqrt{2}}=\dfrac{b}{\sqrt{2}}=\dfrac{\sqrt{2}b}{2} \; (cm) \)
点 \( P \) は線分 \( AF \) の中点なので，
\( PF=\dfrac{AE-EF}{2}
\)
\( =\dfrac{\dfrac{\sqrt{2}a}{2}-\dfrac{\sqrt{2}b}{2}}{2} \)
\( =\dfrac{\sqrt{2}(a-b)}{4} \; (cm) \)
\( AE=BE，EF=EG \) より，\( PF=QG \) なので，
\( PE=QE \) であり，\( △PQE \) も直角二等辺三角形になっています。
ここから，\( PQ：PE=\sqrt{2}：1 \) であり，
\( PQ=\sqrt{2}PE \)
\( =\sqrt{2}\left\{ \dfrac{\sqrt{2}(a-b)}{4}+\dfrac{\sqrt{2}b}{2} \right\} \)
\( =\sqrt{2} \times \dfrac{\sqrt{2}(a+b)}{4} \)
\( =\dfrac{a+b}{2} \; (cm) \)
ここまでと同様の考え方から，\( PE=QE=RE=SE \) であり，四角形 \( PQRS \) も正方形なので，
\( l=4PQ=4 \times \dfrac{a+b}{2}=2(a+b)=2a+2b \; (cm) \)
Ｓさんのグループは，【先生が示した問題】をもとにして，次の問題を考えた。
【Ｓさんのグループが作った問題】
\( a，b \) を正の数とし，\( a>b \) とする。
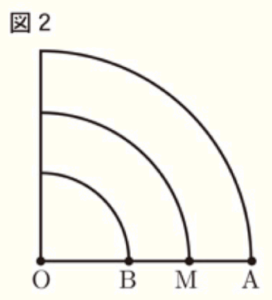
右の図２は，線分 \( OA \) 上にあり，点 \( O \)，点 \( A \) のいずれにも一致しない点を \( B \)，線分 \( AB \) の中点を \( M \) とし，線分 \( OA \)，線分 \( OB \)，線分 \( OM \) を，それぞれ点 \( O \) を中心に反時計回りに \( 90° \) 回転移動させてできた図形である。
図２において，線分 \( OA \) の長さを \( a \; cm \)，線分 \( OB \) の長さを \( b \; cm \)，線分 \( OM \) を半径とするおうぎ形の弧の長さを \( l \; cm \)，線分 \( OA \) を半径とするおうぎ形から，線分 \( OB \) を半径とするおうぎ形を除いた残りの図形の面積を \( S \; cm^2 \) とするとき，\( S=(a-b)l \) となることを確かめてみよう。
〔問２〕 [Ｓさんのグループが作った問題] で，\( l \) を \( a，b \) を用いた式で表し，\( S=(a-b)l \) となることを証明せよ。
ただし，円周率は \( \pi{} \) とする。
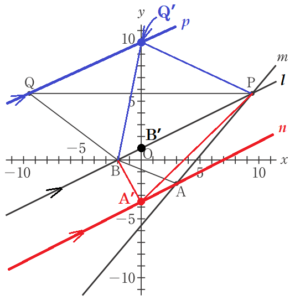
大問３
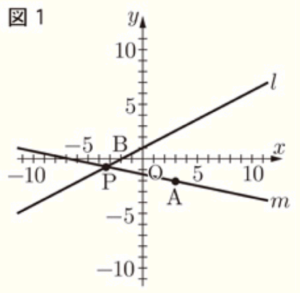
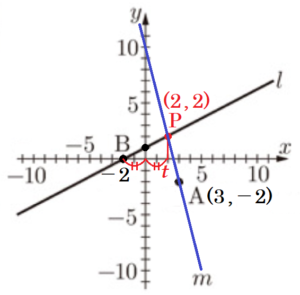
右の図１で，点 \( O \) は原点，点 \( A \) の座標は \( (3，-2) \) であり，直線 \( l \) は一次関数 \( y=\dfrac{1}{2}x+1 \) のグラフを表している。
直線 \( l \) と \( x \) 軸との交点を \( B \) とする。
直線 \( l \) 上にある点を \( P \) とし，２点 \( A，P \) を通る直線を \( m \) とする。
次の各問に答えよ。
〔問１〕 点 \( P \) の \( y \) 座標が \( -1 \) のとき，点 \( P \) の \( x \) 座標を，次のア～エのうちから選び，記号で答えよ。
ア \( -1 \) イ \( -\dfrac{5}{2} \) ウ \( -3 \) エ \( -4 \)
〔問２〕 次の \( \fbox{ ➀ } \) と \( \fbox{ ➁ } \) に当てはまる数を，下のア～エのうちからそれぞれ選び，記号で答えよ。
\( y= \fbox{ ➀ } \; x+ \; \fbox{ ➁ } \)
である。
\( \fbox{ ➀ } \) ア \( -6 \) イ \( -4 \) ウ \( -3 \) エ \( -\dfrac{5}{2} \)
\( \fbox{ ➁ } \) ア \( 5 \) イ \( \dfrac{11}{2} \) ウ \( 7 \) エ \( 10 \)
点 \( B \) は，直線 \( l \) 上の点で，\( x \) 軸との交点なので，
点 \( B \) の座標は \( B(-2，0) \) になります。
線分 \( BP \) が \( y \) 軸により二等分されるということは，
直線 \( l \) と \( y \) 軸の交点 \( (0，1) \) が
線分 \( BP \) の中点になるので，
点 \( P \) の \( x \) 座標を \( t \) とすると，
\( \dfrac{-2+t}{2}=0 \)
\( -2+t=0 \)
\( t=2 \)
点 \( P \) の \( x \) 座標が \( 2 \) のときの \( y \) 座標の値は，
\( y=\dfrac{1}{2} \times 2+1=2 \)
なので，点 \( P \) の座標は \( P(2，2) \) となります。
直線 \( m \) は，\( P(2，2)，A(3，-2) \) を通るので，
傾き \( \fbox{ ➀ } =\dfrac{-2-2}{3-2}=-4 \)
\( y=-4x+\fbox{ ➁ } \) に \( x=2，y=2 \) を代入すると，
\( 2=-4 \times 2+\fbox{ ➁ } \)
\( \fbox{ ➁ }=10 \)
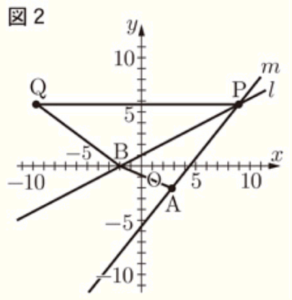
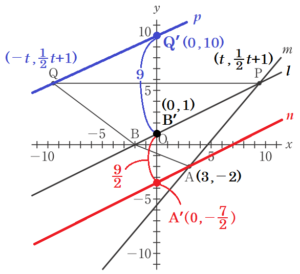
〔問３〕 右の図２は，図１において，点 \( P \) の\( x \) 座標が \( 0 \) より大きい数であるとき，\( y \) 軸を対称の軸として点 \( P \) と線対称な点を \( Q \) とし，点 \( A \) と点 \( B \)，点 \( B \) と点 \( Q \)，点 \( P \) と点 \( Q \) をそれぞれ結んだ場合を表している。
\( △BPQ \) の面積が \( △APB \) の面積の２倍であるとき，点 \( P \) の \( x \) 座標を求めよ。
点 \( A \) を通り，直線 \( l \) と平行な直線を \( n \)，
点 \( Q \) を通り，直線 \( l \) と平行な直線を \( p \)
とし，
直線 \( l \) と \( y \) 軸の交点を \( B’ \)，
直線 \( n \) と \( y \) 軸の交点を \( A’ \)，
直線 \( p \) と \( y \) 軸の交点を \( Q’ \)，
とすると，
等積変形になるので，
\( △BPQ=△BPQ’，△APB=△A’PB \)
になっています。
\( △BPQ=2△APB \) のとき，\( B’Q’=2A’B’ \) になります。
\( A’，B’ \) の座標は具体的にわかるので，\( A’B’ \) の長さもわかります。
そこから，\( B’Q’=2A’B’ \) となるような条件を求めていきます。
直線 \( n \) の式を \( y=\dfrac{1}{2}x+b \) とすると，
\( A(3，-2) \) を通るので，
\( -2=\dfrac{1}{2} \times 3+b \)
\( b=-\dfrac{7}{2} \)
ここから，点 \( A’ \) の座標は \( A’ \left( 0，-\dfrac{7}{2} \right) \)
点 \( B’ \) は，直線 \( l \) と \( y \) 軸の交点なので，
点 \( B’ \) の座標は \( B’(0，1) \)
\( A’ \left( 0，-\dfrac{7}{2} \right)，B’(0，1) \) より，
\( A’B’=1-\left( -\dfrac{7}{2} \right)=\dfrac{9}{2} \)
\( B’Q’=2A’B’ \) となるとき，\( B’Q’=9 \) より，
点 \( Q’ \) の \( y \) 座標の値は\( 10 \) になるので，
直線 \( p \) の式は \( y=\dfrac{1}{2}x+10 \) となります。
ここで，点 \( P \) の \( x \) 座標の値を \( t \) とすると，\( y \) 座標の値は，\( \dfrac{1}{2}t+1 \) と表すことができます。
また，点 \( Q \) は，\( y \) 軸を対称の軸として点 \( P \) と線対称な点なので，
点 \( Q \) の座標は，\( Q(-t，\dfrac{1}{2}t+1) \) と表すことができます。
直線 \( p \) は，\( Q(-t，\dfrac{1}{2}t+1) \) を通るので，
\( y=\dfrac{1}{2}x+10 \) に \( x=-t，y=\dfrac{1}{2}t+1 \) を代入すると，
\( \dfrac{1}{2}t+1=\dfrac{1}{2} \times (-t)+10 \)
\( \dfrac{1}{2}t+1=-\dfrac{1}{2}t+10 \)
\( t=9 \)
大問４
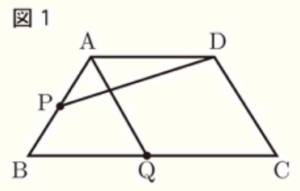
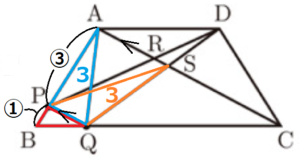
右の図１で，四角形 \( ABCD \) は，\( AD//BC，AB=DC \)，\( AD<BC \) の台形である。
点 \( P \) は，辺 \( AB \) 上にある点で，頂点 \( A \)，頂点 \( B \) のいずれにも
一致しない。
点 \( Q \) は，辺 \( BC \) 上にある点で，頂点 \( B \)，頂点 \( C \) のいずれにも
一致しない。
頂点 \( A \) と点 \( Q \)，頂点 \( D \) と点 \( P \) をそれぞれ結ぶ。
次の各問に答えよ。
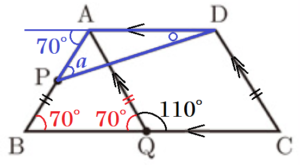
〔問１〕 図１において，\( AQ//DC，∠AQC=110°，∠APD=a° \) とするとき，\( ∠ADP \) の大きさを表す式を，次のア～エのうちから選び，記号で答えよ。
ア \( (140-a) \) 度 イ \( (110-a) \) 度 ウ \( (70-a) \) 度 エ \( (40-a) \) 度
\( AD//BC，AQ//DC \) より，\( AQ=DC \) なので，\( AB=AQ=DC \) であり，
\( △ABQ \) は二等辺三角形になっています。
\( ∠AQB=180°-110°=70° \) なので，
\( ∠ABQ=∠AQB=70° \)
線分 \( AD \) を \( A \) 側に延長し，点 \( R \) をとると，
\( AD//BC \) より，錯角は等しいので，
\( ∠RAB=∠ABQ=70° \)
\( ∠RAB \) は \( △APD \) の外角になっているので，
\( ∠ADP+∠APD=70° \)
\( ∠ADP=70°-a \)
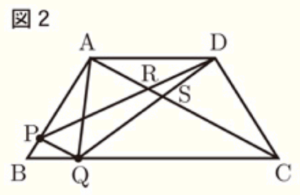
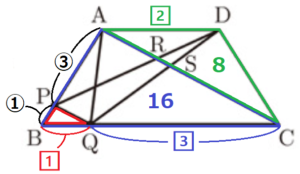
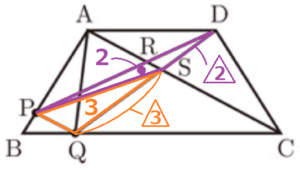
〔問２〕 右の図２は，図１において，
頂点 \( A \) と頂点 \( C \)，頂点 \( D \) と点 \( Q \)，点 \( P \) と点 \( Q \) をそれぞれ結び，線分 \( AC \) と線分 \( DP \) との交点を \( R \)，線分 \( AC \) と線分 \( DQ \) との交点を \( S \) とし， \( AC//PQ \) の場合を表している。
次の➀，➁に答えよ。
➀ \( △ASD \) ∽ \( △CSQ \) であることを証明せよ。
➁ 次の の中の \( \fbox{お}，\fbox{かき} \) に当てはまる数字をそれぞれ答えよ。
\( △DRS \) の面積は，台形 \( ABCD \) の面積の \( \dfrac{ \fbox{お} }{\fbox{かき}} \) 倍である。
\( △DRS \) と台形 \( ABCD \) の面積が\( △BPQ \) の何倍になるかを表すことで
\( △DRS \) と台形 \( ABCD \) の面積比を求めます。
【台形 \( ABCD \) の面積は\( △BPQ \) の何倍か？】
\( △BPQ \) と \( △BAC \) において，
\( △BPQ \) ∽ \( △BAC \)，\( AP：PB=3：1 \) より，
\( △BPQ：△BAC=1：16 \) なので，
\( △BAC \) の面積は「１６」と表すことができます。
\( △ACD \) と \( △BAC \) において，
\( BQ：QC=1：3 \) でもあるので，
\( AD：QC=2：3 \) より，\( AD：BC=2：4 \)
ここから，
\( △ACD：△BAC=2：4=8：16 \) なので，
\( △ACD \) の面積は「８」と表すことができます。
台形 \( ABCD \) は，
\( △BAC \) と \( △ACD \) をくっつけたものなので，
面積は「２４」と表すことができます。 ･･･（ア）
【\( △DRS \) の面積は\( △BPQ \) の何倍か？】
\( △BPQ \) と \( △APQ \) において，
\( AP：PB=3：1 \) より，
\( △BPQ：△APQ=1：3 \) なので，
\( △APQ \) の面積は「３」と表すことができます。
また，\( AC//PQ \) より，等積変形の考え方から
\( △APQ=△SPQ \) なので，
\( △SPQ \) の面積も「３」と表すことができます。
\( △SPQ \) と \( △SPD \) において，
\( △ASD \) ∽ \( △CSQ \)，\( AD：QC=2：3 \) より，
\( SQ：SD=3：2 \) であり，\( △SPQ：△SPD=3：2 \) なので，
\( △SPD \) の面積は「２」と表すことができます。
また，\( △DPQ \) は，
\( △SPQ \) と \( △SPD \) をくっつけたものなので，
面積は「５」と表すことができます。
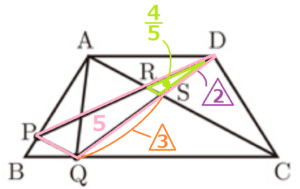
\( △DRS \) と \( △DPQ \) において，
\( △DRS \) ∽ \( △DPQ \)，\( SQ：SD=3：2 \) より，
\( △DRS：△DPQ=4：25 \) なので，
\( △DRS \) の面積は「 \( \dfrac{4}{5} \) 」と表すことができます。 ･･･（イ）
（ア）（イ）より，\( △DRS \) と台形 \( ABCD \) の面積比は，
\( △DRS： \) 台形 \( ABCD=\dfrac{4}{5}：24=1：30 \)
であり，
\( △DRS \) の面積は，台形 \( ABCD \) の面積の \( \dfrac{1}{30} \) 倍 になります。
大問５
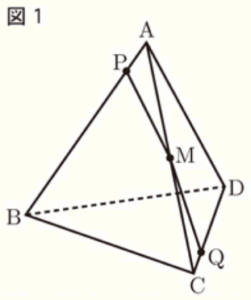
右の図１に示した立体 \( A-BCD \) は，１辺の長さが \( 6 \; cm \) の正四面体である。
辺 \( AC \) の中点を \( M \) とする。
点 \( P \) は，頂点 \( A \) を出発し，辺 \( AB \)，辺 \( BC \) 上を毎秒 \( 1 \; cm \) の速さで動き，\( 12 \) 秒後に頂点 \( C \) に到着する。
点 \( Q \) は，点 \( P \) が頂点 \( A \) を出発するのと同時に頂点 \( C \) を出発し，辺 \( CD \)，辺 \( DA \) 上を点 \( P \) と同じ速さで動き，\( 12 \) 秒後に頂点 \( A \) に到着する。
点 \( M \) と点 \( P \)，点 \( M \) と点 \( Q \) をそれぞれ結ぶ。
次の各問に答えよ。
〔問１〕 次の の中の \( \fbox{く}，\fbox{け} \) に当てはまる数字をそれぞれ答えよ。
\( l \) の値が最も小さくなるのは，点 \( P \) が頂点 \( A \) を出発してから \( \dfrac{\fbox{く}}{\fbox{け}} \) 秒後である。
面 \( ABC \) と面 \( ADC \) に注目し，展開すると右の図のようになります。
また，\( l \) の値が最も小さくなるのは，
線分 \( PQ \) が辺 \( AB，CD \) と垂直になるときです。
\( △ABC，△ADC \) は，ともに正三角形，
点 \( M \) は辺 \( AC \) の中点であることから，
\( △AMP，△CMQ \) は，斜辺が \( 3 \; cm \)で，\( 30°，60°，90° \) の直角三角形になります。
このとき，\( AP=CQ=\dfrac{3}{2} \; cm \) になります。
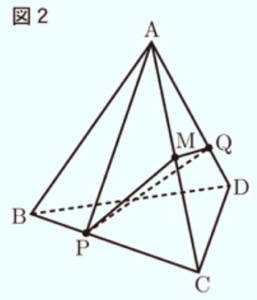
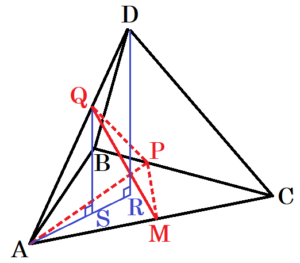
〔問２〕 次の の中の \( \fbox{こ}，\fbox{さ} \) に当てはまる数字をそれぞれ答えよ。
右の図２は，図１において，点 \( P \) が頂点 \( A \) を出発してから
\( 8 \) 秒後のとき，頂点 \( A \) と点 \( P \)，点 \( P \) と点 \( Q \) をそれぞれ
結んだ場合を表している。
立体 \( Q-APM \) の体積は，\( \fbox{こ}\sqrt{\fbox{さ}} \; cm^3 \) である。
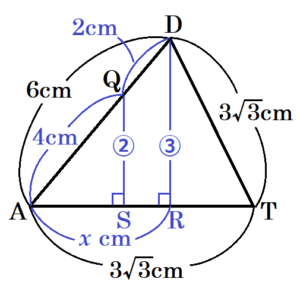
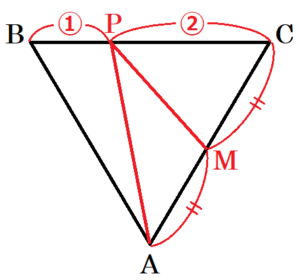
図２の状態のとき，立体 \( A-BCD \) を面 \( ABC \) が底面になるように置き換えると，右の図のようになります。
また，右の図において，点 \( D，Q \) から面 \( ABC \) に垂線をひいたときの交点をそれぞれ点 \( R，S \) とします。
このとき，立体 \( Q-APM \) は，
底面が \( △AMP \)，高さ \( QS \) の三角すいになっています。
点 \( Q \) は辺 \( AD \) 上の点なので，
辺 \( AD \) を通り，面 \( ABC \) と垂直な面で
立体 \( A-BCD \) を切断すると，点 \( D，Q，R，S \) は，この切断面上の点になります。
切断面と辺 \( BC \) の交点を \( T \) とし，
\( AR=x \; cm \) とすると，
\( 6^2-x^2=(3\sqrt{3})^2-(3\sqrt{3}-x)^2 \)
\( 36-x^2=27-(27-6\sqrt{3}x+x^2) \)
\( 6\sqrt{3}x=36 \)
\( x=2\sqrt{3} \; (cm) \)
このとき，
\( DR^2=6^2-(2\sqrt{3})^2=24 \)
\( DR=2\sqrt{6} \; (cm) \)
また，出発してから \( 8 \) 秒後には，\( AQ=4 \; cm，CQ=2 \; cm \) であることから，
\( △ASQ \) と \( △ARD \) の相似比は \( 2：3 \) になるので，
\( QS=\dfrac{2}{3}DR=\dfrac{4\sqrt{6}}{3} \; (cm) \) ･･･（ア）
次に，底面 \( △AMP \) について，
出発してから \( 8 \) 秒後には，
\( BP=2 \; cm，CP=4 \; cm \) であることから，
\( BP：CP=1：2 \) となるので，
\( △ACP=\dfrac{2}{3}△ABC \)
点 \( M \) は，辺\( AC \) の中点なので，
\( △AMP=\dfrac{1}{2}△ACP=\dfrac{1}{3}△ABC \)
\( △ABC \) は１辺 \( 6 \; cm \) の正三角形なので，
\( △ABC=6 \times 3\sqrt{3} \times \dfrac{1}{2}=9\sqrt{3} \; (cm^2) \)
であり，
\( △AMP=\dfrac{1}{3} \times 9\sqrt{3}=3\sqrt{3} \; (cm^2) \) ･･･（イ）
（ア）（イ）より，立体 \( Q-APM \) の体積は，
\( 3\sqrt{3} \times \dfrac{4\sqrt{6}}{3} \times \dfrac{1}{3}=4\sqrt{2} \; (cm^3) \)
