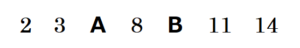大問1
(1) \( 7+4 \times (-2) \) を計算しなさい。
【解説】
\( =7-8 \)
\( =-1 \)
(2) \( xy^3 \times 6x^2y \div 3y^2 \) を計算しなさい。
【解説】
\( =\dfrac{xy^3 \times 6x^2y}{3y^2 } \)
\( =2x^3y^2 \)
(3) \( \sqrt{24}-\sqrt{6} \) を計算しなさい。
【解説】
\( =2\sqrt{6}-\sqrt{6} \)
\( =\sqrt{6} \)
(4) \( 8a+4b-(5a-b) \) を計算しなさい。
【解説】
\( =8a+4b-5a+b \)
\( =3a+5b \)
(5) 連立方程式 \( \left\{ \begin{array}{}
2x+3y=4 \\
5x+4y=3 \\
\end{array} \right. \) を解きなさい。
【解説】
\( \left\{ \begin{array}{}
2x+3y=4 \;\; ・・・ \;\; ➀ \\
5x+4y=3 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁ \( \times 3- \) ➀ \( \times 4 \)
\( 7x=-7 \)
\( x=-1 \)
➀に代入すると,
\( 2 \times (-1)+3y=4 \)
\( 3y=6 \)
\( y=2 \)
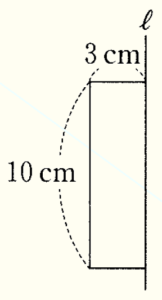
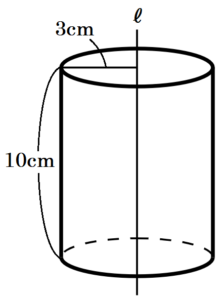
(6) 右の図は,縦 \( 10 \; cm \),横 \( 3 \; cm \) の長方形である。
この長方形を,直線 \( ℓ \) を軸として1回転させてできる立体の体積を求めなさい。
ただし,円周率は \( \pi{} \) とする。
【解答】
\( 90\pi{} \; cm^3 \)
【解説】
図の長方形を回転させると,底面の半径が \( 3 \; cm \),高さが \( 10 \; cm \) の円柱になるので,体積は,
\( \pi{} \times 3^2 \times 10=90\pi{} \; (cm^3) \)
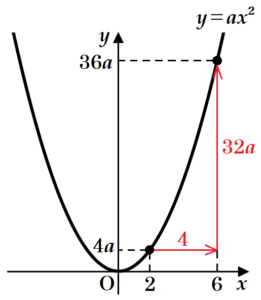
(7) 関数 \( y=ax^2 \) について,\( x \) の値が \( 2 \) から \( 6 \) まで増加するときの変化の割合が \( 12 \) であるとき,\( a \) の値を求めなさい。
【解答】
\( a=\dfrac{3}{2} \)
【解説】
\( y=ax^2 \) について,
\( x=2 \) のときの \( y \) 座標の値は,
\( y=a \times 2^2=4a \)
\( x=6 \) のときの \( y \) 座標の値は,
\( y=a \times 6^2=36a \)
なので,
変化の割合は
\( \dfrac{36a-4a}{6-2}=8a \)
と表すことができます。
よって,
\( 8a=12 \)
\( a=\dfrac{3}{2} \)
(8) ある博物館の入館料は,おとな1人が \( a \) 円,中学生1人が \( b \) 円で,おとな4人と中学生3人の入館料の合計が \( 7000 \) 円以下であった。これらの数量の関係を不等式で表しなさい。
(9) 袋の中に \( 1,2,3,4,5 \) の数が1つずつ書かれた同じ大きさの玉が5個入っている。中を見ないで,この袋から同時に2個の玉を取り出すとき,取り出した玉に書かれた数の積が偶数となる確率を求めなさい。
ただし,どの玉を取り出すことも同様に確からしいものとする。
【解説】
取り出した2個の玉の組み合わせとその積を樹形図に書き出してみます。
積が偶数になる組み合わせは7通り,すべての組み合わせは10通りなので,
求める確率は,\( \dfrac{7}{10} \)

【別解】
2つの数の積が奇数になるのは
奇数 \( \times \) 奇数
の場合になります。
奇数は \( 1,3,5 \) の3つなので,
2個とも奇数を取り出すときの組み合わせは,
\( 1 \) と \( 3 \),\( 1 \) と \( 5 \),\( 3 \) と \( 5 \)
の3通り
ここから,積が奇数になる確率は \( \dfrac{3}{10} \) なので,
積が偶数になる確率は \( 1-\dfrac{3}{10}=\dfrac{7}{10} \)
(偶数・奇数の積の組み合わせ)
偶数 \( \times \) 偶数 \( = \) 偶数
偶数 \( \times \) 奇数 \( = \) 偶数
奇数 \( \times \) 偶数 \( = \) 偶数
奇数 \( \times \) 奇数 \( = \) 奇数
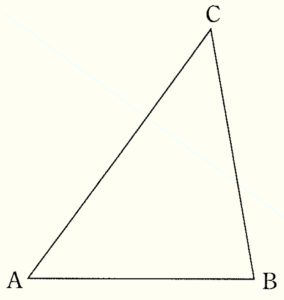
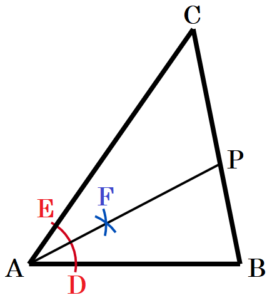
(10) 右の図のような \( △ABC \) がある。辺 \( AB \) が辺 \( AC \) に重なるように \( △ABC \) を折ったときの,折り目の線分と辺 \( BC \) との交点を \( P \) とする。この点 \( P \) を作図によって求め,\( P \) の記号をつけなさい。
ただし,作図に用いた線は残しておくこと。
【解答】
手順1 点 \( A \) を中心に円弧を描く。
(辺 \( AB,AC \) との交点をそれぞれ
点 \( D,E \) とします。)
手順2 2点 \( D,E \) を中心に円弧を描く。
(交点を点 \( F \) とします。)
手順3 2点 \( A,F \) を通る直線を描く。
手順3の直線と辺 \( BC \) との交点が,
求める点 \( P \) になります。
【解説】
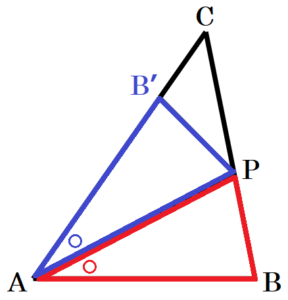
辺 \( AB \) が辺 \( AC \) に重なるように \( △ABC \) を折ったときの,点 \( B \) の移動先を点 \( B’ \) とすると,折り返す前後の図形は合同なので,\( △ABP≡△AB’P \)
対応する角のは等しいので,\( ∠BAP=∠B’AP \)
よって,折り目の直線 \( AP \) は \( ∠BAC \) の二等分線になります。
大問2
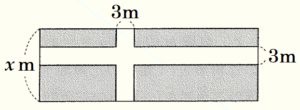
右の図のように,横の長さが縦の長さの3倍である長方形の土地があり,その中に道幅 \( 3 \; m \) で,互いに垂直な道を縦と横につくった。残りの土地を畑にすると,畑の面積が \( 297 \; m^2 \) になった。もとの長方形の土地の縦の長さを求めたい。
かおるさんとひなたさんは,もとの長方形の土地の縦の長さを \( x \; m \) として,それぞれ次の方程式をつくった。
このとき,あとの問いに答えなさい。
かおるさんがつくった方程式
左辺と右辺のどちらも,畑の面積を表している
方程式をつくると,
\( ( \) ① \( )( \) ➁ \( )=297 \)
ひなたさんがつくった方程式
左辺と右辺のどちらも,道の面積を表している
方程式をつくると,
➂ \( =3x^2-297 \)
(1) かおるさんがつくった方程式の ① , ② にあてはまる式を,\( x \) を使った式でそれぞれ表しなさい。
【解答】
① ・・・ \( x-3 \)
② ・・・ \( 3x-3 \)
【解説】
この土地の左端と下端につくったとすると,下の図のようになります。
このとき,畑は,縦 \( x-3 \; m \),横 \( 3x-3 \; m \) の長方形になります。
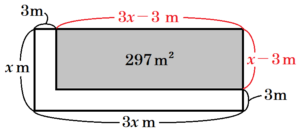
(2) ひなたさんがつくった方程式の ③ にあてはまる式を,\( x \) を使った式で表しなさい。
【解説】
この土地の左端と下端につくったとすると,下の図のようになります。
このとき,道は,
縦 \( x-3 \; m \),横 \( 3 \; m \) の長方形と縦 \( 3 \; m \),横 \( 3x \; m \) の長方形を
くっつけた形になるので,
\( 3(x-3)+3 \times 3x=12x-9 \; (m^2) \)
と表すことができます。
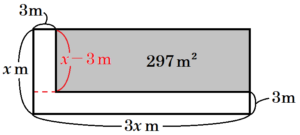
(3) もとの長方形の土地の縦の長さを求めなさい。
【解説】
かおるさんがつくった方程式を解くと,
\( (x-3)(3x-3)=297 \)
\( 3(x-3)(x-1)=297 \)
\( (x-3)(x-1)=99 \)
\( x^2-4x+3=99 \)
\( x^2-4x-96=0 \)
\( (x+8)(x-12)=0 \)
\( x=12 \) (\( x>0 \) より)
よって,求める長さは \( 12 \; m \)
大問3
あるグループの7人が15問の○×クイズに挑戦した。下の図1は,7人の正解した問題数のデータを,箱ひげ図に表したものである。
このとき,次の問いに答えなさい。
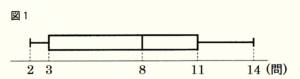
(1) 7人のデータの四分位範囲を求めなさい。
【解説】
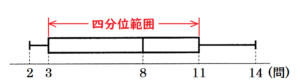
四分位範囲は「第三四分位数」\( – \)「第一四分位数」で求めることができます。
(2) あとから,みずきさんが同じ15問の○×クイズに挑戦した。下の図2は,7人とみずきさんを合わせた8人の正解した問題数のデータを,箱ひげ図に表したものである。
このとき,次の問いに答えなさい。
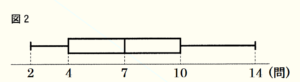
① みずきさんの正解した問題数として,考えられる値は2つある。その値をそれぞれ求めなさい。
【解説】
7人の正解数を少ない方から順番に並べ替えると,
第一四分位数は2番目,中央値は4番目,第三四分位数は6番目の値になるので,
わからない値をA,Bとすると,次のようになります。
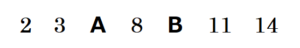
図1と図2を比較すると,最大値と最小値はどちらも同じなので,
みずきさんの正解数は,下のア~カのどこかに入ることがわかります。

8人の正解数で箱ひげ図を描くとき,
第一四分位数は2番目と3番目の平均値,中央値は4番目と5番目の平均値,
第三四分位数は6番目と7番目の平均値
になります。
みずきさんの正解数を \( x \) と考えると,
ア(2番目)に入ると仮定すると,2番目の値が \( x \),3番目の値が \( 3 \),第一四分位数が \( 4 \) になるので,
\( \dfrac{x+3}{2}=4 \) となり,これを解くと,\( x=5 \)
\( x=2,3 \) でなければならないので,これはあてはまりません。
カ(7番目)に入ると仮定すると,6番目の値が \( 11 \),7番目の値が \( x \),第三四分位数が \( 10 \) になるので,
\( \dfrac{11+x}{2}=10 \) となり,これを解くと,\( x=9 \)
\( 11≦x≦14 \) でなければならないので,これはあてはまりません。
エ(5番目)に入ると仮定すると,4番目の値が \( 8 \),5番目の値が \( x \),中央値が \( 7 \) になるので,
\( \dfrac{8+x}{2}=7 \) となり,これを解くと,\( x=6 \)
\( 8≦x≦11 \) でなければならないので,これはあてはまりません。
オ(6番目)に入ると仮定すると,4番目の値が \( 8 \),5番目の値が \( B \),中央値が \( 7 \) になるので,
\( \dfrac{8+B}{2}=7 \) となり,これを解くと,\( B=6 \)
\( 8≦B≦11 \) でなければならないので,これはあてはまりません。
イ(3番目)に入ると仮定すると,2番目の値が \( 3 \),3番目の値が \( x \),第一四分位数が \( 4 \) になるので,
\( \dfrac{3+x}{2}=4 \) となり,これを解くと,\( x=5 \)
このとき,4番目の値が \( A \),5番目の値が \( 8 \),中央値が \( 7 \) になるので,
\( \dfrac{A+8}{2}=7 \) となり,これを解くと,\( A=6 \)
これはあり得ます。
ウ(4番目)に入ると仮定すると,4番目の値が \( x \),5番目の値が \( 8 \),中央値が \( 7 \) になるので,
\( \dfrac{x+8}{2}=7 \) となり,これを解くと,\( x=6 \)
このとき,2番目の値が \( 3 \),3番目の値が \( A \),第一四分位数が \( 4 \) になるので,
\( \dfrac{3+A}{2}=4 \) となり,これを解くと,\( A=5 \)
これはあり得ます。
以上より,みずきさんの正解した問題数として,考えられる値は5問または6問
➁ 8人のデータの平均値を求めなさい。
【解説】
\( x=5,6 \) のとき,6番目の値が \( B \),7番目の値が \( 11 \),第三四分位数が \( 10 \) になるので,
\( \dfrac{B+11}{2}=10 \) となり,これを解くと,\( B=9 \)
このとき,8人の正解数は少ない方から
\( 2,3,5,6,8,9,11,14 \)
となるので,平均値は,
\( \dfrac{2+3+5+6+8+9+11+14}{8}=7.25 \)(問)
大問4
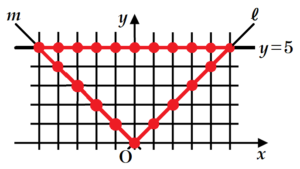
2直線 \( ℓ,m \) と \( x \) 軸に平行な直線の合わせて3つの直線で三角形をつくる。直線 \( ℓ \) の式は \( y=x \),直線 \( m \) の式は \( y=-x \) である。下の図1のように,\( x \) 軸に平行な直線が直線 \( y=1 \) のときの三角形を「\( 1 \) 番目の三角形」,直線 \( y=2 \) のときの三角形を「\( 2 \) 番目の三角形」,直線 \( y=3 \) のときの三角形を「\( 3 \) 番目の三角形」とする。以下,このように,「\( 4 \) 番目の三角形」,「\( 5 \) 番目の三角形」,・・・ をつくっていく。
ただし,三角形をつくる \( x \) 軸に平行な直線と \( y \) 軸との交点の \( y \) 座標は自然数とする。
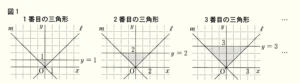
また,点 \( (0,0),(1,2),(-2,3) \)のように,\( x \) 座標,\( y \) 座標がともに整数である点を格子点という。
このとき,次の問いに答えなさい。
(1) 下の図2にある・は三角形の周上にある格子点を表しており,その個数について考える。例えば,「\( 3 \) 番目の三角形」の周上にある格子点の個数は \( 12 \) 個である。
このとき,あとの問いに答えなさい。
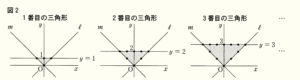
① 「\( 5 \) 番目の三角形」の周上にある格子点の個数を求めなさい。
➁ 「\( n \) 番目の三角形」の周上にある格子点の個数を,\( n \) を使って表しなさい。
【解説】
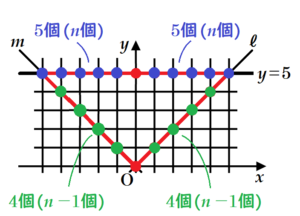
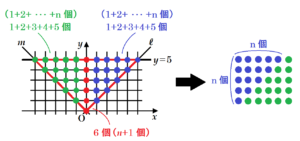
下の図は,\( n=5 \) の例で考えたものです。
\( n \) 個のかたまりが2個,\( n-1 \) 個のかたまりが2個,どちらにも含まれない点が2個あるので,
全部で \( 2n+2(n-1)+2=4n \)(個)
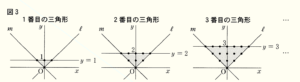
(2) 下の図3にある・は三角形の周上にある格子点と内部にある格子点を表しており,その個数の合計を考える。例えば,「\( 3 \) 番目の三角形」の格子点の個数の合計は \( 16 \) 個である。このとき,格子点の個数の合計がはじめて \( 200 \) 個以上となるのは「何番目の三角形」か求めなさい。
【解説】
格子点の個数の合計は,
「\( 1 \) 番目の三角形」・・・ \( 4=2^2 \) 個
「\( 2 \) 番目の三角形」・・・ \( 9=3^2 \) 個
「\( 3 \) 番目の三角形」・・・ \( 16=4^2 \) 個
・・・
となるので,
「\( n \) 番目の三角形」・・・ \( (n+1)^2 \) 個
となります。
\( 10^2=100,20^2=400 \) より,\( (n+1)^2=200 \) となる \( n+1 \) の値は,
\( 10≦n+1≦20 \) の範囲にあるとわかります。
\( n+1=15 \) のとき,\( (n+1)^2=225 \)
\( n+1=14 \) のとき,\( (n+1)^2=196 \)
なので,はじめて \( 200 \) 個以上となるのは,\( n+1=15 \),
つまり,\( n=14 \) のときなので,「\( 14 \) 番目の三角形」
「n番目の三角形」の格子点が(n+1)²個であることの証明
下の図は,\( n=5 \) の例で考えたものです。
\( 1+2+ \;\; ・・・ \;\; +n \) 個のかたまりが2個,\( n+1 \) 個のかたまりが1個にわけられます,
\( 1+2+ \;\; ・・・ \;\; +n \) 個のかたまり2個の合計個数は \( n(n+1) \)(個)になるので,
全部で \( n(n+1)+n+1=(n+1)^2 \)(個)
大問5
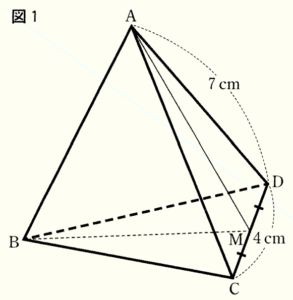
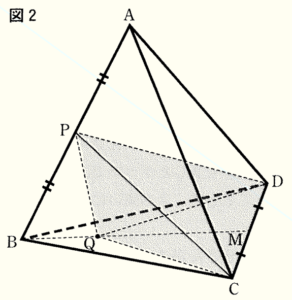
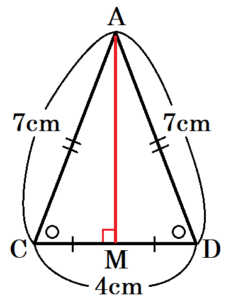
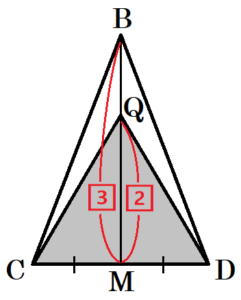
右の図1のような \( AC=AD=BC=BD=7cm,CD=4cm \) の三角すい \( ABCD \) がある。辺 \( CD \) の中点を \( M \) とすると,\( AB=BM=AM \) である。
このとき,次の問いに答えなさい。
(1) 線分 \( AM \) の長さを求めなさい。
【解答】
\( 3\sqrt{5} \; cm \)
【解説】
\( △ACD \) は \( AC=AD \) の二等辺三角形で,
\( M \) は辺 \( CD \) の中点であることから,
\( AM⊥CD \) なので,三平方の定理より,
\( AM^2=7^2-2^2=45 \)
\( AM=3\sqrt{5} \; (cm) \)
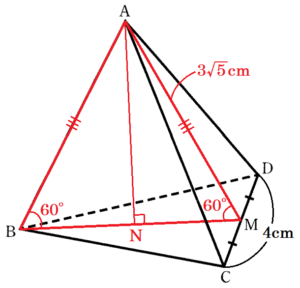
(2) 三角すい \( ABCD \) の体積を求めなさい。
【解答】
\( 15\sqrt{3} \; cm^3 \)
【解説】
\( △ACD,△BCD \) はどちらも \( 7 \; cm,7 \; cm,4 \; cm \) の二等辺三角形なので,
この2面に注目するとひし形 \( ACBD \) を
対角線 \( CD \) で折り曲げた形になっています。
ここから,点 \( A \) から面 \( BCD \) に垂線をひき,
交点を \( N \) とすると,
点 \( N \) は線分 \( BM \) 上の点になります。
\( △ABM \) は1辺 \( 3\sqrt{5} \; cm \) の正三角形なので,
\( AN=\dfrac{\sqrt{3}}{2}AM=\dfrac{3\sqrt{15}}{2} \; (cm) \)
以上より,三角すい \( ABCD \) の体積は,
\( \left( 4 \times 3\sqrt{5} \times \dfrac{1}{2} \right) \times \dfrac{3\sqrt{15}}{2} \times \dfrac{1}{3}=6\sqrt{5} \times \dfrac{\sqrt{15}}{2} \)
\( =15\sqrt{3} \; (cm^3) \)
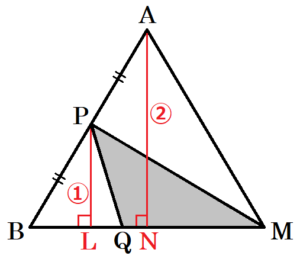
(3) 右の図2のように,辺 \( AB \) の中点を \( P \) とし,線分 \( BM \) 上に点 \( Q \) をとる。三角すい \( PQCD \) の体積が三角すい \( ABCD \) の体積の \( \dfrac{1}{3} \) となるとき,線分 \( QM \) の長さを求めなさい。
【解答】
\( 2\sqrt{5} \; cm \)
【解説】
三角すい \( ABCD \) の高さ \( AN=H_1 \),底面積 \( △BCD=S_1 \),
三角すい \( PQCD \) の高さ \( PL=H_2 \),底面積 \( △QCD=S_2 \)
とすると,
三角すい \( ABCD \) の体積は,\( \dfrac{1}{3}S_1H_1 \)
三角すい \( PQCD \) の体積は,\( \dfrac{1}{3}S_2H_2 \)
と表すことができるので,
\( \dfrac{1}{3}S_2H_2=\dfrac{1}{3} \times \left( \dfrac{1}{3}S_1H_1 \right) \)
\( S_2H_2=\dfrac{1}{3}S_1H_1 \)
となります。
面 \( △ABM \) に注目すると,
\( △ABN \) と \( △PBL \) において,
\( AN//PL \) なので,中点連結定理より,
\( PL=\dfrac{1}{2}AN \)
\( H_2=\dfrac{1}{2}H_1 \)
ここから,
\( S_2H_2=\dfrac{1}{3}S_1H_1 \)
\( \dfrac{1}{2}S_2H_1=\dfrac{1}{3}S_1H_1 \)
\( S_2=\dfrac{2}{3}S_1 \)
面 \( △BCD \) に注目すると,
\( △BCD \) と \( △QCD \) は,底辺 \( CD \) が共通なので,面積比は高さの比と等しくなります。
ここから,\( S_2=\dfrac{2}{3}S_1 \) であるとき,
\( QM=\dfrac{2}{3}BM=\dfrac{2}{3} \times 3\sqrt{5}= 2\sqrt{5} \; (cm) \)
大問6
Aさん,Bさん,Cさんの自宅をそれぞれA宅,B宅,C宅とする。A宅,B宅,C宅,図書館がこの順に一直線の道路沿いにあり,A宅からB宅までは \( 900 \; m \),A宅からC宅までは \( 1200 \; m \),A宅から図書館までは \( 2100 \; m \) はなれている。Aさん,Bさん,Cさんの3人は,次の のように,来週の日曜日に図書館へ行く計画を立てた。
・Aさんは1人でA宅からB宅へ行き,AさんとBさんの2人でB宅からC宅へ行き,Aさん,Bさん,
Cさんの3人でC宅から図書館へ行くことにした。
・3人は毎分 \( 60 \; m \) の速さで歩いていくことにして,図書館に到着する時刻を決め,Aさんの出発時刻,
B宅とC宅のそれぞれでの待ち合わせ時刻を計画した。
ところが,日曜日当日,AさんがおくれてA宅を出発したので,次のア~カのようになった。
ア BさんはB宅での待ち合わせ時刻から \( 5 \) 分間待っていたが,Aさんが来なかったので,Aさんを迎えに
行くために,A宅に向かってB宅を出発した。
イ BさんはB宅からA宅に向かって毎分 \( 60 \; m \) の速さで \( 5 \) 分間歩いたところで,A宅からB宅に向かっ
て毎分 \( 120 \; m \) の速さで走ってきたAさんと出会った。
ウ 出会ったAさんとBさんは,すぐにC宅に向かって毎分 \( 120 \; m \) の速さで走った。
エ CさんはC宅での待ち合わせ時刻から \( 5 \) 分間待っていたが,2人が来なかったので,C宅から図書館に
向かって毎分 \( 30 \; m \) の速さで歩いた。
オ AさんとBさんがC宅に到着したときにはすでにCさんが出発していたので,すぐにAさんとBさんは
毎分 \( 120 \; m \) の速さのままC宅から図書館へ向かったところ, Cさんに追いついた。
カ AさんとBさんがCさんに追いついたあと,3人一緒に図書館に向かった。
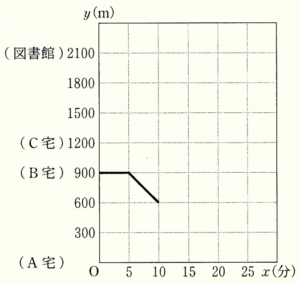
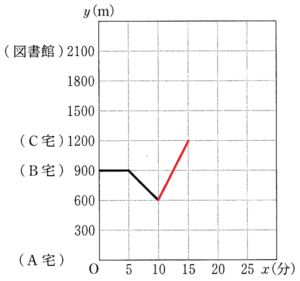
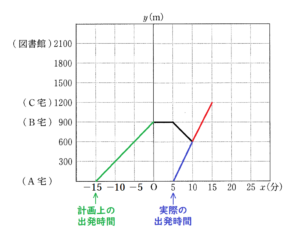
右の図は,BさんがB宅での待ち合わせ時刻から \( x \) 分後に,A宅から \( y \; m \) はなれた地点にいるとして,BさんがAさんと出会うまでの \( x \) と \( y \) の関係を表したグラフである。
このとき,次の問いに答えなさい。
(1) BさんがAさんと出会ってからC宅に到着するまでのグラフを右の図にかき入れなさい。
【解答・解説】
AさんとBさんは,
A宅から \( 600 \; m \) の場所で出会った後,
C宅まで毎分 \( 120 \; m \) の速さで走ったので,
かかった時間は, \( \dfrac{1200-600}{120}=5 \) (分)。
これをグラフに書き込むと右の図のようになります。
(2) Aさんは計画より何分おくれてA宅を出発したか求めなさい。
【解説】
【AさんがA宅を出発した時間】
AさんはA宅を出発してから毎分 \( 120 \; m \) の速さで走ったので,
これをグラフに書き込むと,下の図の青の直線になります。
グラフから,AさんがA宅を出発したのは \( x=5 \) のとき。
【計画上のAさんがA宅を出発する時間】
計画上のB宅での待ち合わせ時刻と場所を表す座標は \( (0,900) \) で,
Aさんは,B宅までの \( 900 \; m \) を毎分 \( 60 \; m \) の速さで歩く予定だったので,
AさんがB宅までの歩くのにかかる時間は \( \dfrac{900}{60}=15 \)(分)
これをグラフに書き込むと,下の図の緑の直線になります。
つまり,計画されていたAさんがA宅を出発する時間は \( x=-15 \) のとき。
よって, Aさんは計画より \( 5-(-15)=20 \) 分遅れて出発したことになります。
(3) AさんとBさんは,A宅から何 \( m \) はなれた地点でCさんに追いついたか求めなさい。
【解説】
Cさんに追いついた場所は,Cさんが歩いた状態を表す直線とAさんとBさんが走った状態を表す直線の
交点としてグラフ上に表されるので,
この2つの直線の式を連立方程式として解いていきます。
【C宅での待ち合わせ時刻】
(2)の緑の直線は計画通りに歩いたときの状態を表しているので,
この直線を \( y=1200 \) まで伸ばしたときの \( x \) の値は \( x=5 \) であり,
これがC宅での待ち合わせ時刻になります。
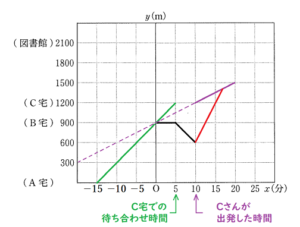
【Cさんが歩いた状態を表す直線の式】
Cさんは.待ち合わせ時刻から \( 5 \) 分後に出発したので,出発したのは \( x=10 \) のとき。
出発してから毎分 \( 30 \; m \) の速さで歩いたので,これをグラフに書き込むと,紫の直線になります。
この直線を延長すると,\( y=900 \) で \( y \) 軸と交わるので,
この直線の式は \( y=30x+900 \) ・・・ ➀
【AさんとBさんが出会ってからCさんに追いつくまでに歩いた状態を表す直線の式】
(1)の赤の直線がAさんとBさんが出会ってから歩いた状態を表していて,
この直線を延長すると,\( y=-600 \) で \( x \) 軸と交わるので,
この直線の式は \( y=120x-600 \) ・・・ ➁
紫と赤の直線の交点がCさんに追いついた時間と場所を表すので,
上の2つの式を連立方程式として解くと,
\( x=\dfrac{50}{3},y=1400 \) となるので,
追いついたのは,A宅から何 \( 1400 \; m \) はなれた地点になります。
(4) AさんとBさんがCさんに追いついたあと,3人ははじめに計画していた毎分 \( 60 \; m \) の速さで歩いて図書館に向かった。計画より何分何秒おくれて図書館に到着するか求めなさい。
【解答】
\( 8 \) 分 \( 20 \) 秒
【解説】
【計画上,図書館に到着する時刻】
(2)の緑の直線は計画通りに歩いたときの状態を表しているので,
この直線を \( y=2100 \) まで伸ばしたときの \( x \) の値は \( x=20 \) であり,
これが計画上の図書館への到着時刻になります。
【Cさんに追いついてから図書館まで歩いた状態を表す直線】
3人は,\( (x,y)=\left(\dfrac{50}{3},1400\right) \) で出会い,
そこから毎分 \( 60 \; m \) の速さで歩いたので,これをグラフに書き込むと,水色の直線になります。
このとき,緑の直線と水色の直線はどちらも毎分 \( 60 \; m \) の速さで歩いた状態を表す直線なので,
平行になっています。
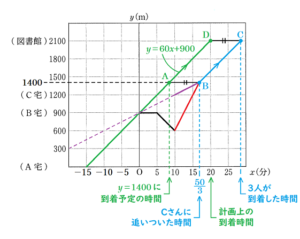
ここで,緑の直線と水色の直線について,
計画上,\( y=1400 \) の場所に到着する予定の点を点 \( A \),
Cさんに追いついた点を点 \( B \),
3人が図書館に到着した点を点 \( C \),
計画上,図書館に到着する予定の点を点 \( D \),
とすると,図書館への到着が計画よりおくれた時間は線分 \( CD \) の長さとして求めることができます。
また,\( AB//CD,AD//BC \) より四角形 \( ABCD \) は平行四辺形になっていることから,
\( AB=CD \) なので,\( AB \) の長さを求めることで遅れた時間を求めます。
緑の直線の式は,\( y=60x+900 \) であり,点 \( A \) の \( y \) 座標は \( 1400 \) なので,
\( x \) 座標は,
\( 1400=60x+900 \)
\( 500=60x \)
\( \dfrac{25}{3}=x \)
点 \( B \) の \( x \) 座標は \( \dfrac{50}{3} \) であることから,
図書館への到着が計画よりおくれた時間は
\( \dfrac{50}{3}-\dfrac{25}{3}=\dfrac{25}{3}=8+\dfrac{1}{3} \)(分)
\( \dfrac{1}{3} \) 分を秒に換算すると,\( 60 \times \dfrac{1}{3}=20 \)(秒)
なので,求める答えは \( 8 \) 分 \( 20 \) 秒。
大問7
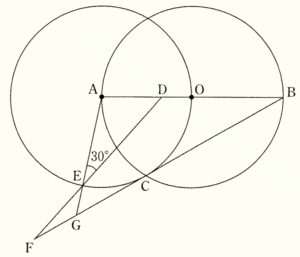
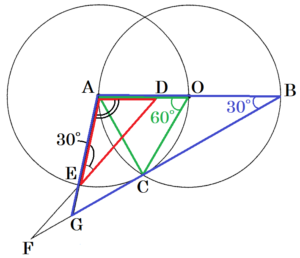
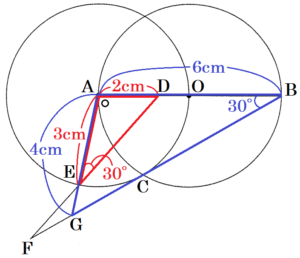
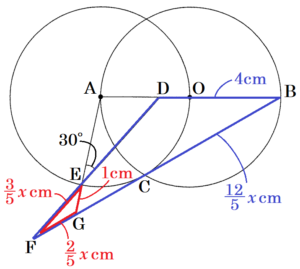
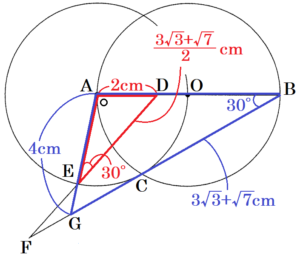
右の図のように,点 \( O \) を中心とし,線分 \( AB \) を直径とする円 \( O \) と,点 \( A \) を中心とし,線分 \( AO \) を半径とする円 \( A \) がある。円 \( O \) と円 \( A \) の交点のうち,一方を \( C \) とする。また,線分 \( AB \) を3等分する点のうち,点 \( A \) に近い方を \( D \) とし,円 \( A \) の周上に \( ∠AED=30° \) となるように点 \( E \) をとる。ただし,点 \( E \) は円 \( O \) の外側にあり,直線 \( AB \) について点 \( C \) と同じ側にあるものとする。また,直線 \( BC \) と直線 \( DE,AE \) の交点をそれぞれ \( F,G \) とする。
このとき,次の問いに答えなさい。
(1) 次の【証明】は,\( △OAC \) が正三角形であることを示し,そのことを用いて \( △AED \) ∽ \( △ABG \) を証明したものである。この【証明】を完成させなさい。
【証明】
\( △OAC \) において,
\( OA,OC \) は円 \( O \) の半径であるから,\( OA=OC \)
\( AO,AC \) は円 \( A \) の半径であるから,\( AO=AC \)
よって,\( OA=OC=AC \)
3つの辺が等しいから,\( △OAC \) は正三角形である。
したがって,\( ∠OAC=∠AOC=∠OCA=60° \)
\( △AED \) と \( △ABG \) において
\( △AED \) ∽ \( △ABG \)
【解答】
\( △AED \) と \( △ABG \) において
\( ∠AOC \) は弧 \( AC \) の中心角
\( ∠ABC \) は弧 \( AC \) の円周角
なので,\( ∠ABC=\dfrac{1}{2}∠AOC=30° \)
\( ∠ABG=∠ABC \) であり,
\( ∠AED=30° \) より,
\( ∠AED=∠ABG \) ・・・ ➀
\( ∠A \) は共通 ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △AED \) ∽ \( △ABG \)
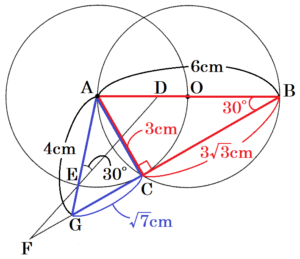
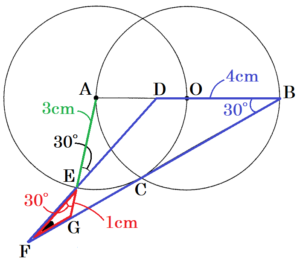
(2) \( AB=6 \; cm,AG=4 \; cm \) のとき,次の問いに答えなさい。
① 線分 \( BG \) の長さを求めなさい。
【解答】
\( (3\sqrt{3}+\sqrt{7}) \; cm \)
【解説】
\( △ABC \) において,
直径に対する円周角なので,\( ∠ACB=90° \)
(1)より \( ∠ABC=30° \)
なので,
\( AC=\dfrac{1}{2}AB=3 \; (cm) \)
\( BC=\dfrac{\sqrt{3}}{2}AB=3\sqrt{3} \; (cm) \)
\( △AGC \) において,三平方の定理より,
\( CG^2=4^2-3^2=7 \)
\( CG=\sqrt{7} \; (cm) \) (\( CG>0 \) より)
よって,
\( BG=(3\sqrt{3}+\sqrt{7}) \; cm \)
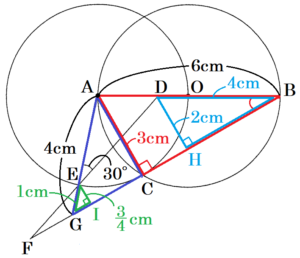
➁ \( △EFG \) の面積を求めなさい。
【解答】
\( \dfrac{9\sqrt{3}+3\sqrt{7}}{40} \; cm \)
【解説】
\( △AED \)∽\( △ABG \),\( AB=6 \; cm,AG=4 \; cm \),
\( AD=\dfrac{1}{3}AB=2 \; cm \) より,
相似比は
\( AD:AG=AE:AB \)
\( 2:4=AE:6 \)
\( AE=3 \; (cm) \)
ここから,\( EG=AG-AE=1 \; (cm) \)
\( △EGF \) と \( △BDF \) において,
対頂角は等しいので,\( ∠GEF=∠AED \)
(1)より,\( ∠DBF=∠AED \)
ここから,\( ∠GEF=∠DBF \) ・・・ ➀
また,\( ∠F \) は共通 ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △EGF \) ∽ \( △BDF \)
相似比は,\( EG:DB=1:4 \)
点 \( D,E \) から線分 \( BF \) に垂線をひき,
交点を \( H,I \) とすると,
\( △ABC \) ∽ \( △DBH \) であり,
\( AB=6 \; cm,AC=3 \; cm,DB=4 \; cm \) なので,
\( AB:DB=AC:DH \)
\( 6:4=3:DH \)
\( DH=2 \; (cm) \)
\( △AGC \) ∽ \( △EGI \) であり,
\( AG=4 \; cm,AC=3 \; cm,EG=1 \; cm \) なので,
\( AG:EG=AC:EI \)
\( 4:1=3:EI \)
\( EI=\dfrac{3}{4} \; (cm) \)
\( △EFI \) と \( △DFH \) において,
\( ∠EIF=∠DHF=90° \),\( ∠F \) は共通
より,2組の角がそれぞれ等しいので,
\( △EFI \) ∽ \( △DFH \)
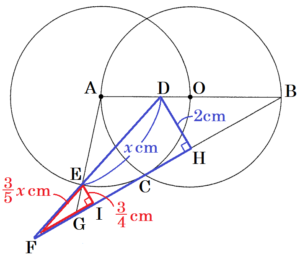
相似比は,\( EI:DH=\dfrac{3}{4}:2=3:8 \)
\( EF:DF=3:8 \) より,\( DE=x \; cm \) とすると,
\( EF:DE=3:5 \)
\( EF:x=3:5 \)
\( EF=\dfrac{3}{5}x \; (cm) \)
\( △EGF \) ∽ \( △BDF \) で,相似比は \( 1:4 \) なので,
\( GF:DF=1:4 \)
\( GF:\dfrac{8}{5}x=1:4 \)
\( GF=\dfrac{2}{5}x \; (cm) \)
以上より,
\( △EFG=GF \times EI \times \dfrac{1}{2} \)
\( =\dfrac{2}{5}x \times \dfrac{3}{4} \times \dfrac{1}{2} \)
\( =\dfrac{3}{20}x \; (cm^2) \)
\( △AED \) ∽ \( △ABG \),\( AD=2 \; cm,AG=4 \; cm,BG=(3\sqrt{3}+\sqrt{7}) \; cm \) より,
\( AD:AG=x:BG \)
\( 2:4=x:(3\sqrt{3}+\sqrt{7}) \)
\( x=\dfrac{3\sqrt{3}+\sqrt{7}}{2} \; (cm) \)
なので,
\( △EFG=\dfrac{3}{20}x \)
\( =\dfrac{3}{20} \times \dfrac{3\sqrt{3}+\sqrt{7}}{2} \)
\( =\dfrac{9\sqrt{3}+3\sqrt{7}}{40} \; (cm^2) \)