大問1
(1) \( 9+21 \div (-3) \) を計算しなさい。
【解説】
\( =9+(-7) \)
\( =2 \)
(2) \( -5^2 \times 2 \) を計算しなさい。
【解説】
\( =-25 \times 2 \)
\( =-50 \)
(3) \( \sqrt{24} \times \sqrt{5} \div \sqrt{15} \) を計算しなさい。
【解説】
\( =2\sqrt{6} \times \sqrt{5} \div \sqrt{15} \)
\( =\dfrac{2\sqrt{6} \times \sqrt{5}}{\sqrt{15}} \)
\( =\dfrac{2\sqrt{6}}{\sqrt{3}} \)
\( =2\sqrt{2} \)
(4) \( 3a+4-2(a-2) \) を計算しなさい。
【解説】
\( =3a+4-2a+4 \)
\( =a+8 \)
(5) 連立方程式 \( \left\{ \begin{array}{}
\dfrac{1}{3}x+\dfrac{1}{2}y=4 \\
5x-3y=18 \\
\end{array} \right. \) を解きなさい。
【解説】
\( \left\{ \begin{array}{}
\dfrac{1}{3}x+\dfrac{1}{2}y=4 \;\; ・・・ \;\; ➀ \\
5x-3y=18 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 6 \)
\( 2x+3y=24 \) ・・・ ➀’
➀’\( + \) ➁
\( 7x=42 \)
\( x=6 \)
➀’に代入すると,
\( 2 \times 6+3y=24 \)
\( 3y=12 \)
\( y=4 \)
(6) 2次方程式 \( 2x^2-7x+4=0 \) を解きなさい。
【解答】
\( x=\dfrac{7±\sqrt{17}}{4} \)
【解説】
解の公式より,
\( x=\dfrac{-(-7)±\sqrt{(-7)^2-4 \times 2 \times 4}}{2 \times 2} \)
\( =\dfrac{7±\sqrt{49-32}}{4} \)
\( =\dfrac{7±\sqrt{17}}{4} \)
(7) \( y \) は \( x \) に反比例し,\( x=-2 \) のとき \( y=8 \) である。\( y \) を \( x \) の式で表しなさい。
【解答】
\( y=-\dfrac{16}{x} \)
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \) ( \( a \) は定数) になります。
\( y=\dfrac{a}{x} \) に \( x=-2,y=8 \) を代入すると,
\( 8=\dfrac{a}{-2} \)
\( a=-16 \)
よって,求める式は \( y=-\dfrac{16}{x} \)
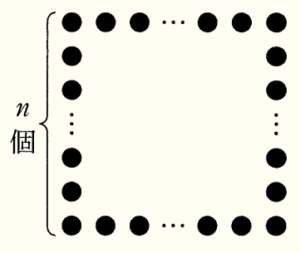
(8) 右の図のように,1辺に \( n \) 個ずつ碁石を並べて,正方形の形をつくる。
このとき,必要な碁石の個数を \( n \) を使った式で表しなさい。
ただし,\( n \) は \( 2 \) 以上の自然数とする。
【解説】
例として,\( n=2,n=3,n=4,n=5 \) それぞれの場合について,
各色の個数が等しくなるように4色に色分けして考えると,次のようになります。
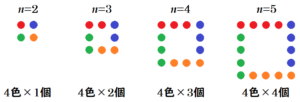
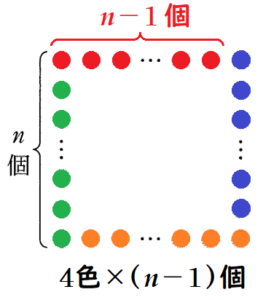
これらを参考に,1辺に \( n \) 個ずつ並べた場合を考えると,下の図のようになるので,
必要な碁石の個数は,\( 4 \times (n-1)=4n-4 \)(個)
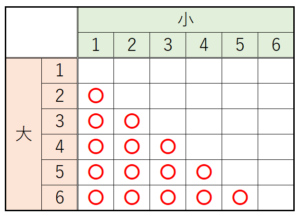
(9) 大小2つのさいころを同時に投げるとき,大きいさいころの出る目の数が,小さいさいころの出る目の数より大きくなる確率を求めなさい。
ただし,それぞれのさいころの \( 1 \) から \( 6 \) までのどの目が出ることも同様に確からしいものとする。
【解説】
大きいさいころの出る目の数と小さいさいころの出る目の数の組み合わせを表に書き出し,大きいさいころの出る目の数が小さいさいころの出る目の数より大きくなるところに 〇 をつけてみます。
大きいさいころの出る目の数が小さいさいころの出る目の数より大きくなる組み合わせは \( 15 \) 通り,
全ての組み合わせは \( 36 \) 通りなので,
求める確率は \( \dfrac{15}{36}=\dfrac{5}{12} \)
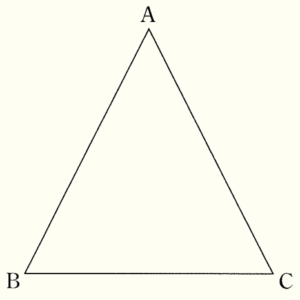
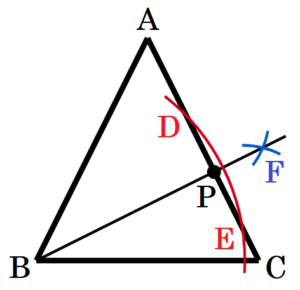
(10) 右の図のように,\( ∠BAC=54°,AB=AC \) である二等辺三角形 \( ABC \) がある。辺 \( AC \) 上にあり,\( ∠ABP=36° \) となる点 \( P \) を作図によって求め,\( P \) の記号をつけなさい。
ただし,作図に用いた線は残しておくこと。
【解答】
手順1 点 \( B \) を中心に円弧を描く
(辺 \( AC \) との交点を \( D,E \) とします。)
手順2 2点 \( D,E \) を中心に円弧を描く
(交点を \( F \) とします。)
手順3 2点 \( B,F \) を通る直線を描く
手順3の直線と辺 \( AC \) との交点が
求める点 \( P \) になります。
【解説】
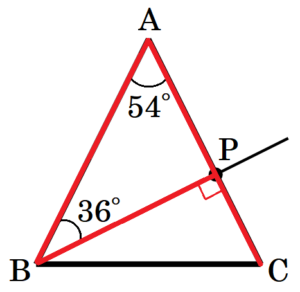
\( ∠BPC \) は \( △ABC \) の外角なので,
\( ∠BAC=54°,∠ABP=36° \) より,
\( ∠BPC=∠BAC+∠ABP \)
\( =54°+36° \)
\( =90° \)
よって,\( BP⊥AC \) になるので,
点 \( B \) を通る辺 \( AC \) の垂線を
描けばいいことになります。
大問2
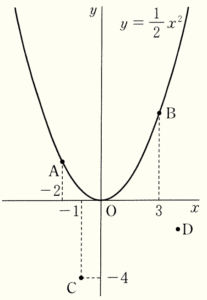
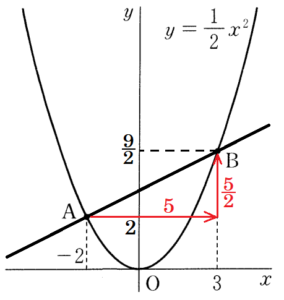
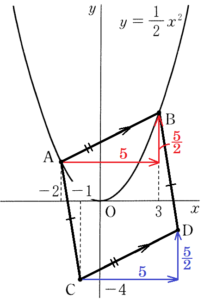
右の図のように,関数 \( y=\dfrac{1}{2}x^2 \) のグラフ上に2点 \( A,B \) があり,\( x \) 座標はそれぞれ \( -2,3 \) である。また,座標平面上に点 \( C(-1,-4) \) をとる。
\( AB=CD,AC=BD \) となるように点 \( D \) をとるとき,次の問いに答えなさい。
(1) 直線 \( AB \) の傾きを求めなさい。
【解説】
点 \( A \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標は \( -2 \) なので,\( y \) 座標の値は,
\( y=\dfrac{1}{2} \times (-2)^2=2 \)
点 \( B \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標は \( 3 \) なので,\( y \) 座標の値は,
\( y=\dfrac{1}{2} \times 3^2=\dfrac{9}{2} \)
直線 \( AB \) の式を \( y=ax+b \) とすると,
直線 \( AB \) は \( A(-2,2),B\left(3,\dfrac{9}{2}\right) \) を通るので,
傾き \( a=\dfrac{\dfrac{9}{2}-2}{3-(-2)}=\dfrac{1}{2} \)
(2) 点 \( D \) の座標を求めなさい。
【解答】
\( D\left(4,-\dfrac{3}{2}\right) \)
【解説】
四角形 \( ACDB \) について考えると,\( AB=CD,AC=BD \) より,
向かい合う2組の辺の長さがそれぞれ等しいことから,平行四辺形になっています。
平行四辺形の向かい合う辺は
それぞれ平行で長さが等しいので,
\( AB//CD,AB=CD \) になっています。
また,(1)より,
点 \( A \) から \( x \) 方向に \( 5 \), \( y \) 方向に \( \dfrac{5}{2} \)
移動した点が点 \( B \) なので,
点 \( C \) から \( x \) 方向に \( 5 \), \( y \) 方向に \( \dfrac{5}{2} \)
移動した点が点 \( D \) になります。
点 \( D \) の座標を \( D(s,t) \) とすると,
\( s=-1+5=4 \)
\( t=-4+\dfrac{5}{2}=-\dfrac{3}{2} \)
なので,点 \( D \) の座標は \( D\left(4,-\dfrac{3}{2}\right) \)
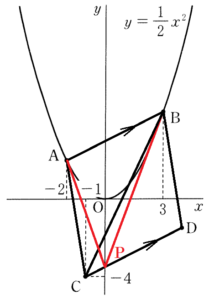
(3) \( y \) 軸上に点 \( P(0,p) \) をとる。\( △ABP \) の面積が四角形 \( ACDB \) の面積の半分となるとき,\( p \) の値を求めなさい。ただし,\( p<0 \) とする。
【解答】
\( p=-\dfrac{7}{2} \)
【解説】
平行四辺形は,対角線によって二等分されるので,
\( △ABC \) の面積は四角形 \( ACDB \) の面積の半分になります。
つまり,\( △ABP \) の面積が\( △ABC \) の面積と等しくなるときの \( p \) の値を求めればいいことに
なります。
\( AB//CD \) より,等積変形の考え方から,
直線 \( CD \) と \( y \) 軸の交点が点 \( P \) になるとき,
\( △ABC=△ABP \) になるので,
直線 \( CD \) の式を \( y=\dfrac{1}{2}x+p \) とし,
\( x=-1,y=-4 \) を代入すると,
\( -4=\dfrac{1}{2} \times (-1)+p \)
\( p=-\dfrac{7}{2} \)
大問3
下の表は,ある中学校の3年A組31人と3年B組32人の反復横とびの記録を,値の小さい方から順に並べたものである。
このとき,あとの問いに答えなさい。

(1) 表1のデータの範囲を求めなさい。
【解説】
範囲 \( = \) 最大値 \( – \) 最小値 で求められるので,
表1のデータの範囲は,\( 62-42=20 \)(回)
(2) 表2のデータの第1四分位数を求めなさい。
【解説】
表2のデータは32人分のデータを集計したものなので,
第1四分位数は回数の少ない方から8番目と9番目の値の平均値になります。
表2から,8番目の値は \( 48 \) 回,9番目の値は \( 50 \) 回なので,
第1四分位数は,\( \dfrac{48+50}{2}=49 \)(回)
(3) 下の図は,表1のデータを箱ひげ図に表したものである。表2のデータを箱ひげ図に表そうとしたところ,表2のデータのうちの1つがまちがっていたことに気づいたので,そのデータを正しい値に直して,あらためてB組のデータとした。この訂正後のB組のデータを箱ひげ図に表すと,下の図と同じ箱ひげ図となった。まちがっていたデータとして考えられる値をすべて求めなさい。
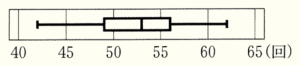
【解答】
\( 53 \),\( 54 \),\( 55 \)
【解説】
表2のデータ(訂正前)と訂正後の箱ひげ図において,最小値,第1四分位数,中央値,第3四分位数,最大値を書き出すと次のようになります。

まず,中央値が \( 53.5 \) 回→ \( 53 \) 回 に変わっていることに注目します。
B組は,全部で32人なので,中央値は回数の少ない方から16番目と17番目の値の平均値になります。
訂正されたデータは1個だけなので,表2で16番目にあたる \( 53 \) 回,17番目にあたる \( 54 \) 回のどちらかは訂正後に16番目または17番目の値になります。
\( 53 \) または \( 54 \) のどちらかを含み,平均値が \( 53 \) になる組み合わせは,
「\( 53 \) と \( 53 \)」,「\( 52 \) と \( 54 \)」の2通りになります。
【16番目の値と17番目の値がどちらも \( 53 \) 回になる場合】
17番目の値が \( 53 \) 回になるということは,「\( 54 \) 回」は18番目の値になります。
このとき,訂正された値は「\( \color{red}{54} \) 回」以上のどれかであることがわかります。
次に,第3四分位数の値に変化がなかったことに注目すると,
24番目と25番目の「\( \color{red}{56} \) 回」という値は変わらないことになります。
これらを整理すると,訂正された(まちがっていた)値は「\( \color{red}{54} \) 回」または「\( \color{red}{55} \) 回」である
ということになります。

【16番目の値が \( 52 \) 回,17番目の値が \( 54 \) 回になる場合】
16番目の値が \( 52 \) 回,17番目の値が \( 54 \) 回になるということは,
「\( 53 \) 回」という値がなくなっています。
つまり,訂正された値は「\( \color{red}{53} \) 回」であることがわかります。
以上より,まちがっていたデータとして考えられる値は,
\( 53 \),\( 54 \),\( 55 \)
の3つになります。
大問4
異なる2つの自然数を自由に選び,小さい方の数を \( a \),大きい方の数を \( b \) とする。\( a \) を2倍した数と \( b \) を5倍した数の和を \( A \),\( a \) を5倍した数と \( b \) を2倍した数の和を \( B \) とし,\( C=A^2-B^2 \) とする。
このとき,次の問いに答えなさい。
(1) \( C \) はつねに,ある自然数の倍数になる。その自然数のうち,もっとも大きいものを求めなさい。
【解説】
\( A,B \) を \( a,b \) を使って表すと,\( A=2a+5b,B=5a+2b \) と表すことができます。
また,\( C=A^2-B^2=(A+B)(A-B) \) なので,ここに代入すると,
\( C=(A+B)(A-B) \)
\( =\{(2a+5b)+(5a+2b)\}\{(2a+5b)-(5a+2b)\} \)
\( =(7a+7b)(-3a+3b) \)
\( =7(a+b) \times 3(-a+b) \)
\( =7(b+a) \times 3(b-a) \)
\( =21(b+a)(b-a) \)
\( a,b \) は自然数,\( b>a \) であることから,\( b+a,b-a \) はどちらも自然数であり,
\( (b+a)(b-a) \) も自然数になります。
よって,\( 21(b+a)(b-a) \) は,\( 21 \) に自然数をかけた数なので,\( 21 \) の倍数になります。
(2) \( \sqrt{C} \) の値が整数となる \( b \) の値のうち,もっとも小さいものを求めなさい。
【解説】
\( \sqrt{C} \) の値が整数となるのは,\( C \) がある整数の2乗になるときです。
(1)より,\( C=21(b+a)(b-a)=3 \times 7 \times (b+a)(b-a) \) なので,
\( C \) がある整数の2乗になり,もっとも小さい値になるのは,
\( (b+a)(b-a)=21=3 \times 7 \)(→ \( C=3 \times 7 \times 3 \times 7=21^2 \) )
のときです。
\( b+a \) は,自然数 \( b \) に自然数 \( a \) を足した数,
\( b-a \) は,自然数 \( b \) から自然数 \( a \) を引いた数
なので,\( b+a>b-a \) になります。
つまり,\( (b+a)(b-a)=3 \times 7 \) のとき,
\( b+a=7,b-a=3 \) になります。
この2つの式を連立方程式として解くと,
\( \left\{ \begin{array}{}
b+a=7 \;\; ・・・ \;\; ➀ \\
b-a=3 \;\; ・・・ \;\; ② \\
\end{array} \right. \)
➀ \( + \) ②
\( 2b=10 \)
\( b=5 \)
(3) \( C \) の値が \( 483 \) であるとき,\( a,b \) の値をそれぞれ求めなさい。
【解説】
(1)より,\( C=21(b+a)(b-a) \) なので,
\( C=483 \)
\( 21(b+a)(b-a)=483 \)
\( (b+a)(b-a)=23 \)
\( 23 \) を自然数の積として表すと,\( 23 \) は素数なので,\( 23 \times 1 \) となります。
このとき,\( b+a>b-a \) になることから,\( b+a=23,b-a=1 \) なので,
連立方程式として解くと,\( a=11,b=12 \)
【参考:\( b+a=23,b-a=1 \) を満たす \( a,b \) の値を連立方程式を使わずに求める】
まず,\( b-a=1 \) より,\( a,b \) は連続する自然数であることがわかります。
次に,\( b+a=23 \) より,連続する自然数の和が \( 23 \) なので,
\( a,b \) は \( 23 \) の半分に近い値であることがわかります。
\( 23 \div 2=11.5 \) であることから,一方の自然数が \( 11 \) であると仮定すると,
\( 23-11=12 \) となり,連続する自然数は \( 11 \) と \( 12 \) であり,
\( b>a \) より,\( a=11,b=12 \) となります。
大問5
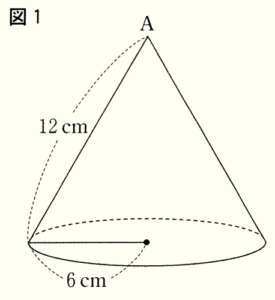
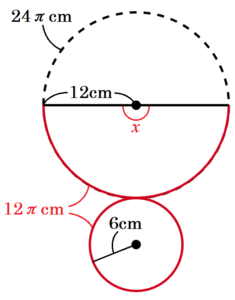
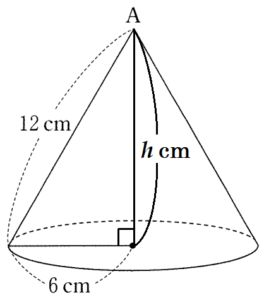
右の図1のように,頂点がA,底面の半径が \( 6 \; cm \),母線の長さが \( 12 \; cm \) の円すいがある。
このとき,次の問いに答えなさい。
ただし,円周率は \( \pi{} \) とする。
(1) この円すいの表面積を求めなさい。
【解答】
\( 108\pi{} \; cm^2 \)
【解説】
円すいの展開図では,側面のおうぎ形の弧の長さと
底面の円周の長さは等しくなっています。
おうぎ形の中心角の大きさは弧の長さに比例するので,おうぎ形の中心角を \( x \) とすると,
\( x=\dfrac{2\pi{} \times 6}{2\pi{} \times 12} \times 360°=180° \)
よって,表面積は
\( \pi{} \times 12^2 \times \dfrac{180°}{360°}+\pi{} \times 6^2=108\pi{} \; (cm^2) \)
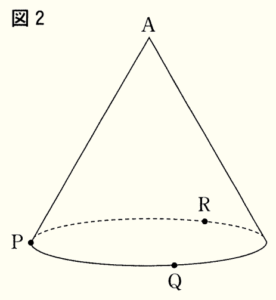
(2) 右の図2のように,底面の円周上に異なる3点 \( P,Q,R \) をとる。このとき,次の問いに答えなさい。
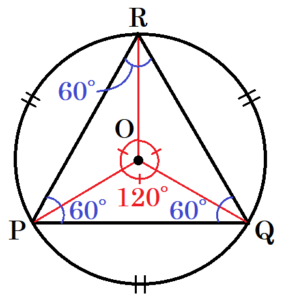
① 3点 \( P,Q,R \) を,円周を3等分するようにとったとき,\( △PQR \) の面積を求めなさい。
【解答】
\( 27\sqrt{3} \; cm^2 \)
【解説】
中心角の大きさは弧の長さに比例することから,
円周が3等分されるとき,中心角も3等分されます。
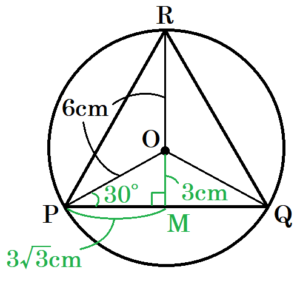
底面の円の中心を \( O \) とすると,
\( ∠POQ=\dfrac{1}{3} \times 360°=120° \)
\( ∠POQ \) は \( \stackrel{\huge\frown}{ PQ } \) の中心角,\( ∠PRQ \) は \( \stackrel{\huge\frown}{ PQ } \) の円周角なので,
\( ∠PRQ=\dfrac{1}{2}∠POQ=60° \)
\( ∠QPR,∠PQR \) についても同じことがいえるので,\( △PQR \) は正三角形になっています。
線分 \( RO \) を延長したときの辺 \( PQ \) との交点を
\( M \) とすると,\( △OPQ \) は \( ∠POQ=120° \) の二等辺三角形なので,
\( ∠OPQ=\dfrac{180°-120°}{2}=30° \)
\( RM⊥PQ \) になることから,
\( △OPM \) は \( 30°,60°,90° \) の直角三角形なので,
\( OM=\dfrac{1}{2}OP=3 \; (cm) \)
\( PM=\dfrac{\sqrt{3}}{2}OP=3\sqrt{3} \; (cm) \)
点 \( M \) は辺 \( PQ \) の中点になるので,
\( PQ=2PM=6\sqrt{3} \; (cm) \)
よって,\( △PQR \) の面積は,
\( △PQR=6\sqrt{3} \times (6+3) \times \dfrac{1}{2}=27\sqrt{3} \; (cm^2) \)
➁ 3点 \( P,Q,R \) を,\( \stackrel{\huge\frown}{ PQ }:\stackrel{\huge\frown}{ QR }:\stackrel{\huge\frown}{ RP }=3:4:5 \) となるようにとったとき,4点 \( A,P,Q,R \) を結んでできる立体の体積を求めなさい。
ただし,\( \stackrel{\huge\frown}{ PQ }:\stackrel{\huge\frown}{ QR }:\stackrel{\huge\frown}{ RP } \) は,それぞれ短い方の弧を指すものとする。
【解答】
\( 54+54\sqrt{3} \; cm^3 \)
【解説】
【方針】
求める三角すいの高さは,図1の円すいの高さと等しいので三平方の定理から簡単に求められます。
つまり,\( △PQR \) の面積を求められればいいことになります。
\( △PQR \) の面積を求めるためには,底辺と高さを求める必要がありますが,
この問題では,長さは \( OP=OQ=OR=6 \; cm \) しか長さの情報がないので,
長さが計算しやすくなるような特徴的な角度を見つけることがポイントになります。
【解法】
中心角の大きさは弧の長さに比例することから,
円周が \( 3:4:5 \) の比で分割されるとき,
それぞれの弧に対する中心角の比も \( 3:4:5 \) なので,
\( ∠POQ:∠QOR:∠ROP=\stackrel{\huge\frown}{ PQ }:\stackrel{\huge\frown}{ QR }:\stackrel{\huge\frown}{ RP } \)
\( =3:4:5 \)
であり,
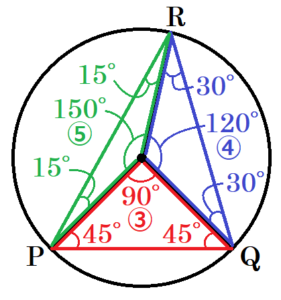
\( ∠POQ=\dfrac{3}{12} \times 360°=90° \)
\( ∠QOR=\dfrac{4}{12} \times 360°=120° \)
\( ∠ROP=\dfrac{5}{12} \times 360°=150° \)
また,\( △OPQ,△OQR,△ORP \) は二等辺三角形なので,
\( ∠OPQ=∠OQP=\dfrac{180°-90°}{2}=45° \)
\( ∠OQR=∠ORQ=\dfrac{180°-120°}{2}=30° \)
\( ∠ORP=∠OPR=\dfrac{180°-150°}{2}=15° \)
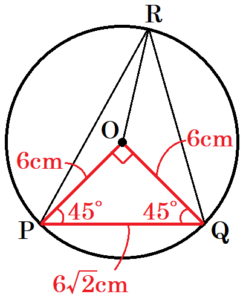
\( △OPQ \) は \( OP=OQ=6 \; cm \) の直角二等辺三角形なので,
\( PQ=\sqrt{2}OP=6\sqrt{2} \; (cm) \)
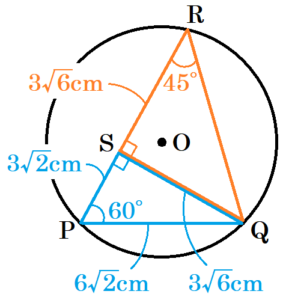
点 \( Q \) から辺 \( RP \) に垂線をひき,交点を \( S \) とすると,
\( △PQS \) は \( 30°,60°,90° \) の直角三角形なので,
\( PS=\dfrac{1}{2}PQ=3\sqrt{2} \; (cm) \)
\( QS=\dfrac{\sqrt{3}}{2}PQ=3\sqrt{6} \; (cm) \)
\( △RQS \) は直角二等辺三角形なので,
\( RS=QS=3\sqrt{6} \; (cm) \)
ここから,
\( RP=RS+PS=3\sqrt{6}+3\sqrt{2} \; (cm) \)
であり,\( △PQR \) の面積は,
\( RP \times QS \times \dfrac{1}{2}=(3\sqrt{6}+3\sqrt{2}) \times 3\sqrt{6} \times \dfrac{1}{2} \)
\( =27+9\sqrt{3} \; (cm^2) \)
また,求める立体の高さを \( h \; cm \) とすると,
三平方の定理より,
\( h^2=12^2-6^2=108 \)
\( h=6\sqrt{3} \; (cm) \)
よって,求める立体の体積は,
\( (27+9\sqrt{3}) \times 6\sqrt{3} \times \dfrac{1}{3}=54+54\sqrt{3} \; (cm^3) \)
大問6
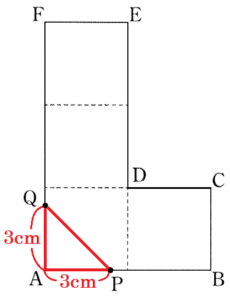
下の図1のように,1辺が \( 4 \; cm \) の正方形を4つ組み合わせたL字型の図形 \( ABCDEF \) がある。点 \( P \) は,\( A \) を出発し,毎秒 \( 1 \; cm \) の速さで,あともどりすることなく辺 \( AB,BC,CD,DE \) 上を \( A→B→C→D→E \) の順に \( E \) まで動き,\( E \) で停止する。点 \( Q \) は,\( A \) を出発し,毎秒 \( 1 \; cm \) の速さで,あともどりすることなく辺 \( AF,FE \) 上を \( A→F→E \) の順に \( E \) まで動き,\( E \) で停止する。
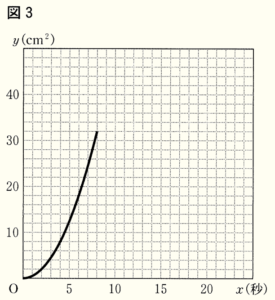
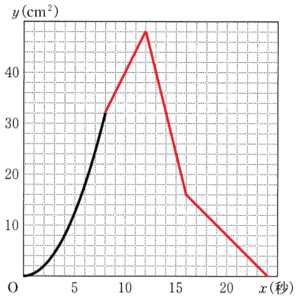
下の図2のように,2点 \( P,Q \) が同時に \( A \) を出発してから \( x \) 秒後の \( △APQ \) の面積を \( y \; cm^2 \) とするとき,あとの問いに答えなさい。
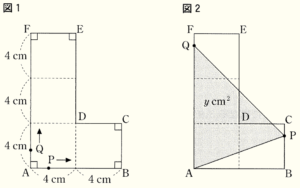
(1) \( x=3 \) のとき,\( y \) の値を求めなさい。
【解答】
\( y=\dfrac{9}{2} \)
【解説】
\( x=3 \) のとき,\( △APQ \) は,右の図のように
\( AP=AQ=3 \; cm,∠PAQ=90° \)
の直角二等辺三角形になるので,
\( y=3 \times 3 \times \dfrac{1}{2}=\dfrac{9}{2} \; (cm^2) \)
(2) 点 \( P \) が辺 \( BC \) 上を動くとき,\( y \) を \( x \) の式で表しなさい。
【解説】
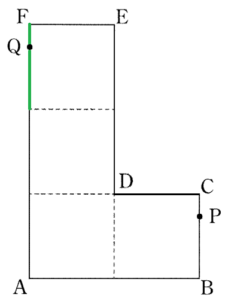
まず,点 \( P \) が辺 \( BC \) 上を動くとき,点 \( Q \) はどこを動いているのかを確認します。
点 \( P \) が点 \( B \) 上にあるのは,\( x=8 \) のとき,
点 \( C \) 上にあるのは,\( x=12 \) のとき
なので,点 \( P \) が辺 \( BC \) 上を動くとき,
点 \( Q \) は右の図の緑の線の部分を動きます。
\( △APQ \) の底辺を \( AQ \) とすると,
点 \( P \) が辺 \( BC \) 上を動くとき,
\( AQ=x \; cm \) であり,
\( AF//BC \) より,高さは常に \( 8 \; cm \) なので,
\( y=x \times 8 \times \dfrac{1}{2}=4x \)
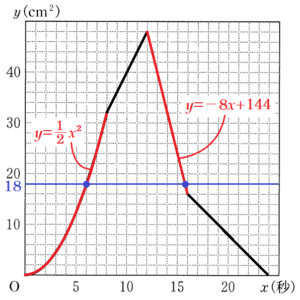
(3) 右の図3は,点 \( P \) が \( A \) を出発してから停止するまでの \( x \) と \( y \) の関係を表したグラフの一部である。このグラフを完成させなさい。
【解説】
\( x \) の値によって,2点 \( P,Q \) がどこを動いているのかを場合分けして考えていきます。
【\( 8≦x≦12 \) の場合】
点 \( P \) が辺 \( BC \) 上を動くときなので,(2)の結果より,\( x \) と \( y \) の関係は \( y=4x \) で表されます。
よって,\( x=12 \) のときの \( y \) の値は,\( y=4 \times 12=48 \)
であり,\( (8,32) \) と \( (12,48) \) をつなぐ直線になります。
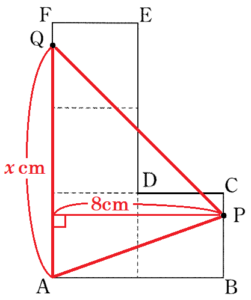
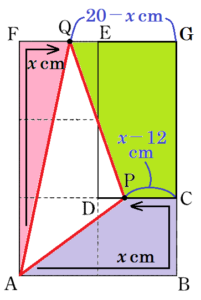
【\( 12≦x≦16 \) の場合】
点 \( P \) は辺 \( CD \) 上,点 \( Q \) は辺 \( FE \) 上を動きます。
辺 \( BC \) と辺 \( FE \) を延長した交点を \( G \) とすると,
\( △APQ= \) 長方形 \( ABGF-(△AFQ+ \) 台形 \( ABCP+ \) 台形 \( QGCP) \)
となっています。
このとき,\( x \) と \( y \) の関係を式で表すと,
\( AB+BC+CP=x \; (cm) \),
\( AB+BC=12 \; (cm) \) より,
\( CP=x-12 \; cm \) ,
\( AF+FQ=x \; (cm) \),
\( AF+FG=20 \; cm \) より,
\( QG=20-x \; cm \)
\( FQ=x-12 \; cm \)
なので,
長方形 \( ABGF=12 \times 8=96 \; (cm^2) \)
\( △AFQ=12 \times (x-12) \times \dfrac{1}{2} \)
\( =6x-72 \; (cm^2) \)
台形 \( ABCP=\{ (x-12)+8 \} \times 4 \times \dfrac{1}{2} \)
\( =2x-8 \; (cm^2) \)
台形 \( QGCP=\{ (20-x)+(x-12) \} \times 8 \times \dfrac{1}{2} \)
\( =32 \; (cm^2) \)
となり,
\( y=96-\{ (6x-72)+(2x-8)+32 \} \)
\( =-8x+144 \)
と表すことができます。
よって,\( x=16 \) のときの \( y \) の値は,\( y=-8 \times 16+144=16 \)
であり,\( (12,48) \) と \( (16,16) \) をつなぐ直線になります。
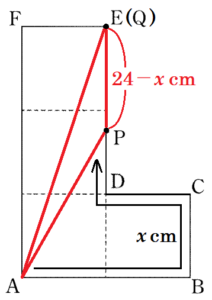
【\( 16≦x≦24 \) の場合】
点 \( P \) は辺 \( DE \) 上を動き,点 \( Q \) は点 \( E \) から動きません。
このとき,\( x \) と \( y \) の関係を式で表すと,
\( AB+BC+CD+DP=x \; (cm) \),
\( AB+BC+CD+DE=24 \; cm \) より,
\( PE=24-x \; cm \)
なので,
\( y=(24-x) \times 4 \times \dfrac{1}{2} \)
\( =-2x+48 \)
と表すことができます。
よって,\( x=24 \) のときの \( y \) の値は,\( y=-2 \times 24+48=0 \)
であり,\( (16,16) \) と \( (24,0) \) をつなぐ直線になります。
(4) \( △APQ \) の面積が \( 18 \; cm^2 \) となる \( x \) の値は2つある。その値をそれぞれ求めなさい。
【解答】
\( x=6,\dfrac{63}{4} \)
【解説】
(3)のグラフは,\( x \) 秒後の \( △APQ \) の面積を \( y \; cm^2 \) として表したものなので,
(3)のグラフにおいて,\( y=18 \) となるときの \( x \) の値を求めればいいことになります。
(3)のグラフに \( y=18 \) の直線をかき加えると,
\( 0≦x≦8 \) の曲線及び \( 12≦x≦16 \) の直線の2本と交わります。
\( 0≦x≦8 \) の曲線の式は \( y=\dfrac{1}{2}x^2 \) なので,\( y=18 \) を代入すると,
\( 18=\dfrac{1}{2}x^2 \)
\( x^2=36 \)
\( x=6 \) (\( x>0 \) より)
\( 12≦x≦16 \) の直線の式は \( y=-8x+144 \) なので,\( y=18 \) を代入すると,
\( 18=-8x+144 \)
\( 8x=126 \)
\( x=\dfrac{63}{4} \)
大問7
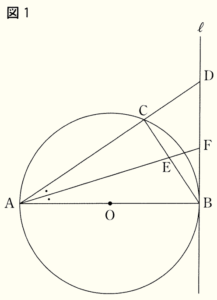
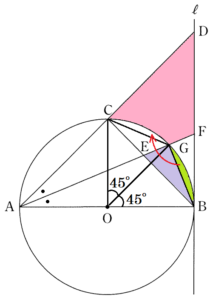
右の図1のように,線分 \( AB \) を直径とする円 \( O \) がある。また,直線 ℓ は点 \( B \) を接点とする円 \( O \) の接線である。
\( \stackrel{\huge\frown}{ AB } \) 上に点 \( C \) をとり,直線 \( AC \) と直線 ℓ との交点を \( D \) とし,\( ∠DAB \) の二等分線と線分 \( BC,BD \) との交点をそれぞれ \( E,F \) とする。
このとき,次の問いに答えなさい。
(1) 次の【証明】は,\( ∠BAE=∠CAE=∠a \) として,\( △BEF \) が二等辺三角形であることを証明したものである。この【証明】を完成させなさい。
【証明】
仮定から
\( ∠BAE=∠CAE=∠a \) ・・・ ①
円の接線は,接点を通る半径に垂直だから,
\( ∠ABF=90° \) ・・・ ➁
三角形の内角の和は \( 180° \) であることと,①,②から
\( ∠BFE=180°-∠ABF-∠BAE \)
\( =90°-∠a \) ・・・ ➂
また,
\( △BEF \) は二等辺三角形である。
【解答】
また,直径に対する円周角だから
\( ∠ACE=90° \) ・・・ ➃
三角形の内角の和は \( 180° \) であることと,①,➃から
\( ∠AEC=180°-∠ACE-∠CAE \)
\( =90°-∠a \)
対頂角は等しいから
\( ∠BEF=∠ACE=90°-∠a \) ・・・ ➄
➂,➄から
\( ∠BFE=∠BEF \)
よって,2つの角が等しいから,
\( △BEF \) は二等辺三角形である。
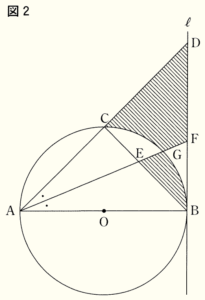
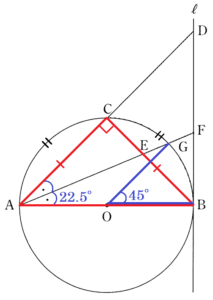
(2) 右の図2のように,点 \( C \) を \( \stackrel{\huge\frown}{ AC }=\stackrel{\huge\frown}{ BC } \) となるようにとり,線分 \( EF \) と \( \stackrel{\huge\frown}{ BC } \) との交点を \( G \) とする。
\( AB=4 \; cm \) のとき,次の問いに答えなさい。
ただし,円周率は \( \pi{} \) とする。
➀ 円周角 \( ∠BAG \) に対する \( \stackrel{\huge\frown}{ BG } \) の長さを求めなさい。
【解答】
\( \dfrac{\pi{}}{2} \)
【解説】
直径に対する円周角なので,\( ∠ACB=90° \)
弧の長さが等しいとき,対応する弦の長さも等しいので,
\( \stackrel{\huge\frown}{ AC }=\stackrel{\huge\frown}{ BC } \) より,\( AC=BC \)
ここから,\( △ACB \) は直角二等辺三角形なので,
\( ∠CAB=45° \)
線分 \( AF \) は \( ∠CAB \) の二等分線なので,
\( ∠BAG=\dfrac{1}{2}∠CAB=22.5° \)
\( ∠BAG \) は \( \stackrel{\huge\frown}{ BG } \) に対する円周角,
\( ∠BOG \) は \( \stackrel{\huge\frown}{ BG } \) に対する中心角なので,
\( ∠BOG=2∠BAG=45° \)
中心角の大きさは弧の長さに比例するので,\( \dfrac{45°}{360°}=\dfrac{1}{8} \) より,
\( \stackrel{\huge\frown}{ BG } \) の長さは,円 \( O \) の円周の長さの \( \dfrac{1}{8} \) になります。
よって,
\( \stackrel{\huge\frown}{ BG }=\pi{} \times 4 \times \dfrac{1}{8}=\dfrac{\pi{}}{2} \)
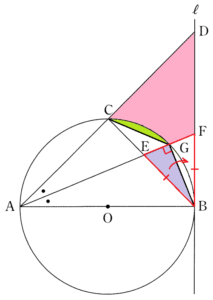
➁ 図2の斜線部分の面積を求めなさい。
【解答】
\( 6-2\sqrt{2} \; cm^2 \)
【解説】
計算しにくい形の面積を求めるときは,計算しやすい形に変形(移動)できないか考えていきます。
補助線 \( BG,CG,OC,OG \) をひくと,斜線部分の面積は,ピンク \( + \) 紫 \( + \) 黄緑 と考えることができます。
【黄緑の部分の場所を移動させる】
➀より,\( ∠CAG=∠BAG=22.5° \) なので,
中心角と円周角の関係から,
\( ∠COG=∠BOG=45° \)
このとき,おうぎ形 \( OBG \) とおうぎ形 \( OCG \),\( △OBG \) と \( △OCG \) はそれぞれ合同であり,
おうぎ形 \( OBG \) から \( △OBG \) を引いた弓形と
おうぎ形 \( OCG \) から \( △OCG \) を引いた弓形
も合同になっています。
合同な図形の面積は等しいので,右の図のように黄緑の部分を移動させても面積は等しくなります。
【紫の部分の場所を移動させる】
(1)より,\( △BEF \) が二等辺三角形であることに
注目すると,
\( ∠EGB \) は直径 \( AB \) に対する円周角なので,
\( ∠EGB=90° \)
であり,\( △BEG≡△BFG \) になっています。
よって,右の図のように紫の部分を移動させることができます。
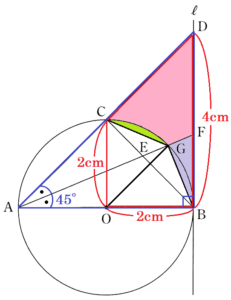
以上のことから,ピンク \( + \) 紫 \( + \) 黄緑 の面積は,
台形 \( OBDC-(△OBG+△OCG) \)
で求めることができます。
【台形 \( OBDC \) の面積を求める】
\( △ABD \) において,
円の直径と接線は接点において垂直に交わるので,
\( ∠ABD=90° \)
問➀より,
\( ∠CAB=45° \)
であり,\( △ABD \) は直角二等辺三角形なので,
\( BD=AB=4 \; cm \)
円 \( O \) の半径なので,
\( OB=OC=2 \; cm \)
よって,台形 \( OBDC \) の面積は,
\( (2+4) \times 2 \times \dfrac{1}{2}=6 \; (cm^2) \)
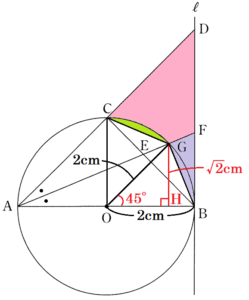
【\( △OBG,△OCG \) の面積を求める】
\( △OBG \) において,点 \( G \) から線分 \( BO \) に垂線をひき,交点を \( H \) とすると,
\( ∠BOG=45° \) より,
\( △OGH \) は直角二等辺三角形になっています。
円 \( O \) の半径なので,
\( OG=2 \; cm \)
であることから,
\( GH=\dfrac{1}{\sqrt{2}}OG=\sqrt{2} \; (cm) \)
よって,\( △OBG \) の面積は,
\( 2 \times \sqrt{2} \times \dfrac{1}{2}=\sqrt{2} \; (cm^2) \)
\( △OBG,△OCG \) は合同なので,
\( △OCG=△OBG=\sqrt{2} \; (cm^2) \)
【ピンク \( + \) 紫 \( + \) 黄緑 の面積を求める】
ピンク \( + \) 紫 \( + \) 黄緑 の面積を \( S \) とすると,
\( S= \) 台形 \( OBDC-(△OBG+△OCG) \)
\( =6-(\sqrt{2}+\sqrt{2}) \)
\( =6-2\sqrt{2} \; (cm^2) \)