大問1
1 次の式を計算しなさい。
(1) \( 1-(2-5) \)
【解説】
\( =1-(-3) \)
\( =1+3 \)
\( =4 \)
(2) \( \dfrac{3}{5} \times \left( \dfrac{1}{2}-\dfrac{2}{3} \right) \)
【解答】
\( -\dfrac{1}{10} \)
【解説】
\( =\dfrac{3}{5} \times \left( \dfrac{3}{6}-\dfrac{4}{6} \right) \)
\( =\dfrac{3}{5} \times \left(-\dfrac{1}{6} \right) \)
\( =-\dfrac{1}{10} \)
(3) \( -12ab \times (-3a)^2 \div 6a^2b \)
【解説】
\( =\dfrac{-12ab \times 9a^2}{6a^2b} \)
\( =-18a \)
(4) \( (\sqrt{7}-2)(\sqrt{7}+3)-\sqrt{28} \)
【解説】
\( =(7+\sqrt{7}-6)-2\sqrt{7} \)
\( =1-\sqrt{7} \)
2 2次方程式 \( (x-7)(x+2)=-9x-13 \) を解きなさい。解き方も書くこと。
【解答】
\( x^2-5x-14=-9x-13 \)
\( x^2+4x-1=0 \)
\( x=\dfrac{-4±\sqrt{16+4}}{2} \)
\( =\dfrac{-4±2\sqrt{5}}{2} \)
\( =-2±\sqrt{5} \)
3 \( x=23,y=18 \) のとき,\( x^2-2xy+y^2 \) の値を求めなさい。
【解説】
\( x^2-2xy+y^2=(x-y)^2 \)
\( x=23,y=18 \) を代入すると,
\( (23-18)^2=25 \)
4 下の図は,山形市,酒田市,新庄市,米沢市における,2022年4月1日から4月30日までの日ごとの最高気温のデータを,それぞれ箱ひげ図に表したものである。あとの ➀~➂ のそれぞれについて,これらの箱ひげ図から読み取れることとして正しいものを〇,正しくないものを×としたとき,〇と×の組み合わせとして適切なものを,あとのア~クから1つ選び,記号で答えなさい。
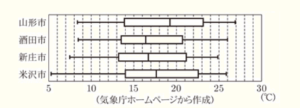
➀ 中央値は,山形市のほうが,酒田市より大きい。
➁ 四分位範囲がもっとも大きいのは,米沢市である。
➂ 最高気温が21°C以上の日数がもっとも少ないのは,新庄市である。
|
ア |
イ |
ウ |
エ |
オ |
カ |
キ |
ク |
| ➀ |
○ |
○ |
○ |
○ |
× |
× |
× |
× |
| ➁ |
○ |
○ |
× |
× |
○ |
○ |
× |
× |
| ➂ |
○ |
× |
○ |
× |
○ |
× |
○ |
× |
【解説】
➀ 中央値は,山形市が約23℃,酒田市が約16.5℃
➁ 四分位範囲の大小は,箱の長さで確認できます。
箱の長さが最も長いのは山形市。
➂ データの総数が30日なので,第三四分位数にあたるのは気温が高い方から8番目の気温になります。
酒田市は第三四分位数が21℃より低いので,最高気温が21°C以上だったのは,7日以下。
他の3市は第三四分位数が21℃以上なので,最高気温が21°C以上だったのは,8日以上。
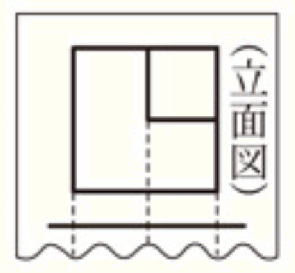
5 右の図は,投影図の一部である。この図から考えられる立体の見取
図として適切でないものを,次のア~エから1つ選び,記号で答えな
さい。
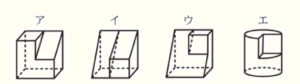
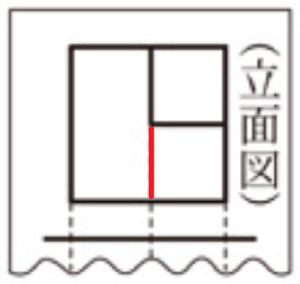
【解答】
イ
イの立面図には下の図の赤線の部分が必要です。
大問2
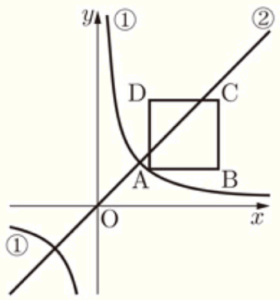
1 右の図において,➀は関数 \( y=\dfrac{a}{x} \) のグラフ,➁は関数 \( y=bx \) のグラフである。
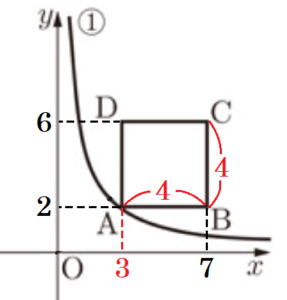
➀のグラフ上に座標が \( 3 \) である点 \( A \) をとり,四角形 \( ABCD \) が正方形となるように,3点 \( B,C,D \) をとると,2点 \( B,C \) の座標は,それぞれ \( (7,2),(7,6) \) となった。このとき,次の問いに答えなさい。
(1) \( a \) の値を求めなさい。
【解説】
正方形はすべての辺の長さが等しいので,
\( B,C \) の座標が,\( (7,2),(7,6) \) であることから,
辺 \( AB,BC \) の長さは \( 4 \) になります。
\( B \) の \( x \) 座標は \( 7 \) なので,\( A \) の \( x \) 座標は \( 3 \) になります。
ここから,\( A \) の座標は,\( (3,2) \) なので,
\( y=\dfrac{a}{x} \) に \( x=3,y=2 \) を代入すると,
\( 2=\dfrac{a}{3} \)
\( a=6 \)
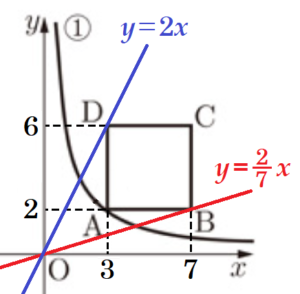
(2) 関数 \( y=bx \) のグラフが四角形 \( ABCD \) の辺上の点を通るとき,\( b \) のとる値の範囲を,不等号を使って表しなさい。
【解答】
\( \dfrac{2}{7}≦b≦2 \)
【解説】
四角形 \( ABCD \) の辺上の点を通るとき,
➁の直線の傾きがもっとも小さくなるのは,
\( B(7,2) \) を通るときなので,
\( y=\dfrac{2}{7}x \) より,\( b=\dfrac{2}{7} \)
➁の直線の傾きがもっとも大きくなるのは,
\( D(3,6) \) を通るときなので,
\( y=2x \) より,\( b=2 \)
よって,求める \( b \) の範囲は,\( \dfrac{2}{7}≦b≦2 \)
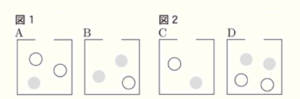
2 純さんと友子さんは,白玉3個と赤玉3個を使い,あることがらの起こりやすさを条件を変えて調べてみることにした。
純さんは,図1のように,Aの箱に白玉2個と赤玉1個,Bの箱に白玉1個と赤玉2個を入れ,A,Bの箱から,それぞれ玉を1個ずつ取り出す。友子さんは,図2のように,Cの箱に白玉1個と赤玉1個,Dの箱に白玉2個と赤玉2個を入れ,C,Dの箱からそれぞれ玉を1個ずつ取り出す。
このとき,2個とも白玉が出ることの起こりやすさについて述べた文として適切なものを,あとのア~ウから1つ選び,記号で答えなさい。また,選んだ理由を確率を使って説明しなさい。
ただし,それぞれの箱において,どの玉が取り出されることも同様に確からしいものとする。
ア 純さんのほうが,友子さんより起こりやすい。
イ 友子さんのほうが,純さんより起こりやすい。
ウ 起こりやすさは2人とも同じである。
【解答】
イ
純さんが2個とも白玉を選ぶ確率は,
Aの箱から白玉が出る確率は \( \dfrac{2}{3} \),Bの箱から白玉が出る確率は \( \dfrac{1}{3} \) なので,
\( \dfrac{2}{3} \times \dfrac{1}{3}=\dfrac{2}{9} \)
友子さんが2個とも白玉を選ぶ確率は,
Cの箱から白玉が出る確率は \( \dfrac{1}{2} \),Dの箱から白玉が出る確率は \( \dfrac{2}{4} \) なので,
\( \dfrac{1}{2} \times \dfrac{2}{4}=\dfrac{1}{4} \)
\( \dfrac{2}{9}≦\dfrac{1}{4} \) なので,友子さんのほうが,純さんより起こりやすい。
(参考)
●ということがらが起こる確率を \( a \),▲ということがらが起こる確率を \( b \) とするとき,
●と▲が両方とも起こる確率は,\( a \times b \) で求めることができます。
3 次の問題について,あとの問いに答えなさい。
〔問題〕
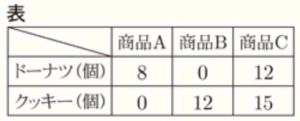
ある洋菓子店では,お菓子を箱に入れた商品A,B,Cをそれぞれ作っています。右の表は,それぞれの商品に入っているお菓子の種類と個数を示したものです。この洋菓子店では,商品A,B,Cを合わせて40箱作り,そのうち,商品Cは10箱作りました。また,40箱の商品を作るために使ったお菓子の個数は,ドーナツのほうが,クッキーより50個少なくなりました。40箱の商品を作るために使ったドーナツは何個ですか。
(1) この問題を解くのに,方程式を利用することが考えられる。どの数量を文字で表すかを示し,
問題にふくまれる数量の関係から,1次方程式または連立方程式のいずれかをつくりなさい。
【解答】
\( \left\{ \begin{array}{}
x+y+10=40 \\
12y+15 \times 10-50=8x+12 \times 10
\end{array} \right. \)
【解説】
商品A,B,Cを合わせて40箱作り,そのうち,商品Cは10箱作ったので,
商品Aを作った数を \( x \) 箱,商品Bを作った数を \( y \) 箱として,
箱数の関係を方程式で表すと,\( x+y+10=40 \)
次に,使ったお菓子の個数の関係を考えると,
使ったドーナツの個数は,\( 8x+12 \times 10 \) 個
使ったクッキーの個数は,\( 12y+15 \times 10 \) 個
使ったお菓子の個数は,ドーナツのほうが,クッキーより50個少なかったので,方程式で表すと,
\( 12y+15 \times 10-50=8x+12 \times 10 \) 個 と表すことができます。
(2) 40箱の商品を作るために使ったドーナツの個数を求めなさい。
【解説】
(1) の連立方程式を解くと,
\( \left\{ \begin{array}{}
x+y+10=40 ・・・ ➀ \\
12y+15 \times 10-50=8x+12 \times 10 ・・・ ➁
\end{array} \right. \)
➀より,
\( x+y=30 \) ・・・ ➀’
➁より,
\( 3y-2x=5 \) ・・・ ➁’
➀’\( \times 3\) すると,
\( 3x+3y=90 \) ・・・ ➀”
➀”-➁すると,
\( 5x=85 \)
\( x=17 \)
よって,使ったドーナツの個数は,
\( 8 \times 17+12 \times 10=256 \) (個)
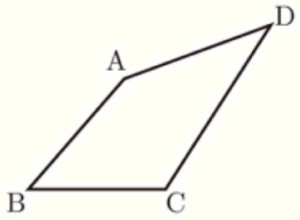
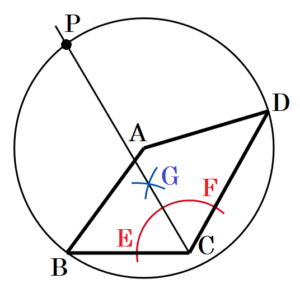
4 右の図において,四角形 \( ABCD \) は,\( AB=AD \) である。下の【条件】1,2をともにみたす点 \( P \) を,定規とコンパスを使って作図しなさい。
ただし,作図に使った線は残しておくこと。
【条件】
1 点 \( P \) は,\( ∠BCD \) を二等分する直線上にあり,直線 \( BC \) の上側の点である。
2 \( ∠BPD \) の大きさは,\( ∠BAD \) の大きさの半分であり,\( 90° \) より小さい。
【解答・解説】
「\( ∠BPD \) の大きさは,\( ∠BAD \) の大きさの半分」ということから,
\( ∠BPD \) と \( ∠BAD \) は,円周角と中心角の関係になっています。
このとき,\( AB=AD \) より,点 \( A \) が円の中心になることがわかります。
ここから,線分 \( AB \) を半径とする円 \( A \) と \( ∠BCD \) の二等分線の交点が点 \( P \) になります。
手順1 点 \( A \) を中心に線分 \( AB \) を半径とする円を描く
手順2 点 \( C \) を中心に線分 \( BC,CD \) と交わるような弧を描く
(交点を点 \( D,E \) とします)
手順3 点 \( E,F \) を中心に弧を描く
(交点を点 \( G \) とします)
手順4 点 \( C,G \) を通る直線を描く
手順1の円と手順4の直線の交点が点 \( P \) になります。
大問3
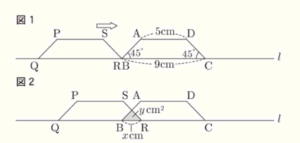
図1において,四角形 \( ABCD \) と四角形 \( PQRS \) は合同であり,\( AD//BC,AD=5 \; cm \),
\( BC=9 \; cm,∠ABC=∠DCB=45° \) である。四角形 \( ABCD \) の辺 \( BC \) と四角形 \( PQRS \) の辺 \( QR \) は直線 \( l \) 上にあって,頂点 \( B \) と頂点 \( R \) は直線 \( l \) 上の同じ位置にある。いま,四角形 \( PQRS \) を直線 \( l \) にそって矢印の方向に移動する。
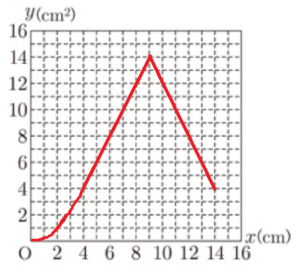
図2のように,四角形 \( PQRS \) を \( x \; cm \) 移動したとき,四角形 \( ABCD \) と四角形 \( PQRS \) が重なっている部分の面積を \( y \; cm^2 \) とする。このとき,それぞれの問いに答えなさい。
1 頂点 \( P \) が頂点 \( D \) と同じ位置にくるまで移動したときの \( x \) と \( y \) の関係を表にかきだしたところ,表1のようになった。次の問いに答えなさい。
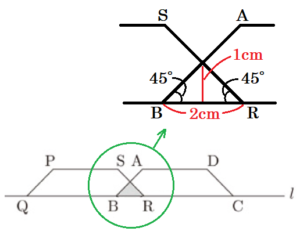
(1) \( x=2 \) のときの \( y \) の値を求めなさい。
【解説】
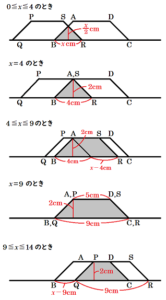
四角形 \( PQRS \) が \( 2 \; cm \) 移動したとき,重なっている部分は,
底辺 \( 2 \; cm \),高さ \( 1 \; cm \) の三角形になります。
(2) 表2は,頂点 \( P \) が頂点 \( D \) と同じ位置にくるまで移動したときの \( x \) と \( y \) の関係を式に表したものである。
\(\fbox{ ア }\) ~ \(\fbox{ ウ }\) にあてはまる数または式を,それぞれ書きなさい。
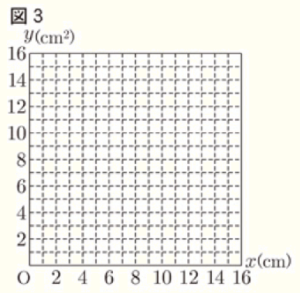
また,このときの \( x \) と \( y \) の関係を表すグラフを図3にかきなさい。

【解答】
\( \fbox{ ア } \) ・・・ \( \dfrac{1}{4}x^2 \)
\( \fbox{ イ } \) ・・・ \( 9 \)
\( \fbox{ ウ } \) ・・・ \( -2x+32 \)
【解説】
\( 0≦x≦4 \) のとき,重なっている部分は,
底辺 \( x \; cm \),高さ \( \dfrac{x}{2} \; cm \) の三角形になるので,
\( y=x \times \dfrac{x}{2} \times \dfrac{1}{2} \)
\( =\dfrac{1}{4}x^2 \; (cm^2) \)。
\( x=4 \) のとき,点 \( A \) と点 \( S \) が重なります。
\( 4≦x≦9 \) のとき,重なっている部分は,
底辺 \( 4 \; cm \),高さ \( 2 \; cm \) の三角形と
底辺 \( x-4 \; cm \),高さ \( 2 \; cm \) の平行四辺形を
くっつけた形になるので,
\( y=\left\{ 4 \times 2 \times \dfrac{1}{2} \right\}+\left\{ (x-4) \times 2 \right\} \)
\( =4+2(x-4) \)
\( =2x-4 \; (cm^2) \)
\( x=9 \) のとき,四角形 \( ABCD \) と四角形 \( PQRS \) はぴったり重なります。
\( 9≦x≦14 \) のとき,四角形 \( ABCD \) から
底辺 \( x-9 \; cm \),高さ \( 2 \; cm \) の平行四辺形を
除いた形になるので,
\( y=\left\{ (5+9) \times 2 \times \dfrac{1}{2} \right\}-\left\{ (x-9) \times 2 \right\} \)
\( =14-2(x-9) \)
\( =-2x+32 \; (cm^2) \)
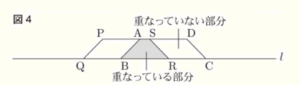
2 図4のように,四角形 \( ABCD \) を,四角形 \( PQRS \) と重なっている部分と,四角形 \( PQRS \) と重なっていない部分に分ける。重なっている部分の面積が,重なっていない部分の面積の2倍となるときの \( x \) の値のうち,最も小さい値を求めなさい。
【解説】
四角形 \( ABCD \) の面積は,\( (5+9) \times 2 \times \dfrac{1}{2}=14 \; (cm^2) \) なので,
重なっている部分の面積が,重なっていない部分の面積の2倍となるとき,
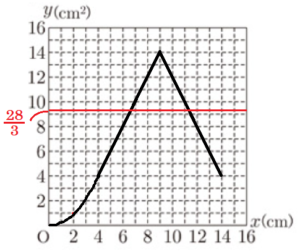
重なっている部分の面積は,\( 14 \times \dfrac{2}{3}=\dfrac{28}{3} \; (cm^2) \)
(2) のグラフに,\( y=\dfrac{28}{3} \) の直線を書き足すと,
\( y=2x-4 \) の直線と \( y=-2x+32 \) の直線と
交わります。
求めるのは小さい方の \( x \) の値ということは,
\( y=\dfrac{28}{3} \) と \( y=2x-4 \) が交わるときなので,
\( 2x-4=\dfrac{28}{3} \)
\( 2x=\dfrac{40}{3} \)
\( x=\dfrac{20}{3} \)
大問4
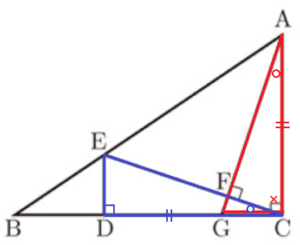
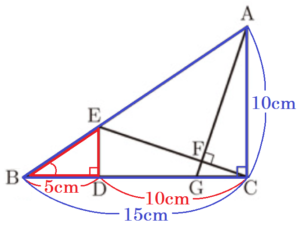
下の図のように, \( ∠ACB=90° \) の \( △ABC \) があり,辺 \( BC \) の長さは辺 \( AC \) の長さよりも長いものとする。点 \( D \) を,辺 \( BC \) 上に,\( AC=CD \) となるようにとる。また,点 \( E \) を,辺 \( AB \) 上に,\( AC//ED \) となるようにとる。点 \( A \) から線分 \( CE \) にひいた垂線と線分 \( CE \) との交点を \( F \) とし,直線 \( AF \) と直線 \( BC \) との交点を \( G \) とする。このとき,あとの問いに答えなさい。
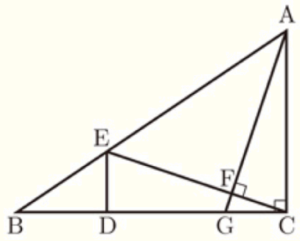
1 \( △AGC≡△CED \) であることを証明しなさい。
【解答】
\( △AGC \) と \( △CED \) において,
仮定より,\( AC=CD \) ・・・ ➀
\( AC//ED,∠ACB=90° \) より,\( ∠ACG=∠CDE=90° \) ・・・ ➁
\( △ACF \) において,
\( ∠CAF=180°-(∠AFC+∠ACF) \)
\( =90°-∠ACF \) ・・・ ➂
\( ∠ACB=90° \) より,
\( ∠DCE=90°-∠ACF \) ・・・ ➃
➂➃より,\( ∠CAG=∠DCE \) ・・・ ➄
➀➁➄より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △AGC≡△CED \)
2 \( AC=10 \; cm,BC=15 \; cm \) であるとき,次の問いに答えなさい。
(1) \( ED \) の長さを求めなさい。
【解答】
\( \dfrac{10}{3} \; cm \)
【解説】
\( ∠BDE=∠BCA=90°,∠B \) 共通 より,\( △BDE \) ∽ \( △BCA \)
\( AC=CD=10 \; cm,BC=15 \; cm \) より,
\( BD=BC-CD=5 \; cm \) なので,
\( ED:AC=BD:BC \)
\( ED:10=5:15 \)
\( ED=\dfrac{10}{3} \; (cm) \)
(2) \( △AFC \) を,直線 \( AC \) を軸として1回転させてできる立体の体積を求めなさい。なお,円周率は \( \pi{} \) とする。
【解答】
\( 30\pi{} \; cm^3 \)
【解説】
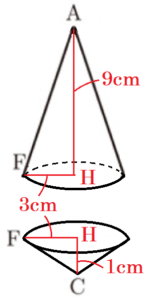
\( △AFC \) を,直線 \( AC \) を軸として1回転させてできる立体は,2つの円すいをくっつけた形になります。
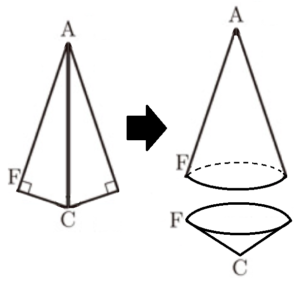
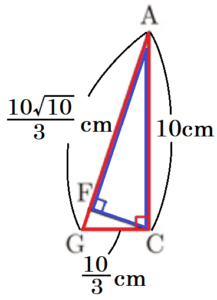
\( △AGC≡△CED \)より,\( GC=ED=\dfrac{10}{3} \; cm \)
\( △AGC \) において,三平方の定理より,
\( AG^2=AC^2+GC^2=\dfrac{1000}{9} \)
\( AG=\dfrac{10\sqrt{10}}{3} \; cm \)
\( ∠ACG=∠AFC=90°,∠A \)共通 より,\( △AGC \) ∽ \( △ACF \)
対応する辺の比は等しいので,
\( AG:AC=AC:AF \)
\( \dfrac{10\sqrt{10}}{3}:10=10:AF \)
\( AF=3\sqrt{10} \; (cm) \)
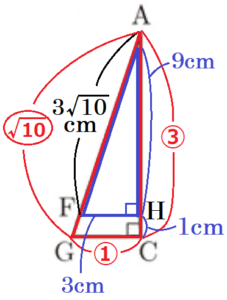
点 \( F \) から線分 \( AC \) に垂線をひき,交点を点 \( H \) とすると,
\( GC:AC:AG=\dfrac{10}{3}:10:\dfrac{10\sqrt{10}}{3}=1:3:\sqrt{10} \) なので,
\( GC:AC:AG=FH:AH:AF \)
\( 1:3:\sqrt{10}=FH:AH:3\sqrt{10} \)
となり,
\( FH=3 \; cm,AH=9 \; cm \)
また,\( AC=10 \; cm \) より, \( CH=AC-AH=1 \; (cm) \)
以上より,求める立体の体積は,
\( \left( \pi{} \times 3^2 \times 9 \times \dfrac{1}{3} \right)+\left( \pi{} \times 3^2 \times 1 \times \dfrac{1}{3} \right) \)
\( =\pi{} \times 3^2 \times (9+1) \times \dfrac{1}{3} \)
\( =30\pi{} \; (cm^3) \)