大問1
1 次の式を計算しなさい。
(1) \( 4-(3-7) \)
【解説】
\( =4-(-4) \)
\( =4+4 \)
\( =8 \)
(2) \( \dfrac{2}{3}+\dfrac{5}{2} \div \left( -\dfrac{9}{4} \right) \)
【解説】
\( =\dfrac{2}{3}+\dfrac{5}{2} \times \left( -\dfrac{4}{9} \right) \)
\( =\dfrac{2}{3}-\dfrac{10}{9} \)
\( =\dfrac{6}{9}-\dfrac{10}{9} \)
\( =-\dfrac{4}{9} \)
(3) \( (18a^2b-12ab) \div (-6ab) \)
【解説】
\( =-\dfrac{18a^2b-12ab}{6ab} \)
\( =-(3a-2) \)
\( =-3a+2 \)
(4) \( (\sqrt{2}+3)(\sqrt{2}-4)+\sqrt{18} \)
【解説】
\( =(-10-\sqrt{2})+3\sqrt{2} \)
\( =-10+2\sqrt{2} \)
2 2次方程式 \( (2x-1)^2=5x-1 \) を解きなさい。解き方も書くこと。
【解答】
\( (2x-1)^2=5x-1 \)
\( 4x^2-4x+1=5x-1 \)
\( 4x^2-9x+2=0 \)
\( (4x-1)(x-2)=0 \)
\( x=\dfrac{1}{4},2 \)
3 \( \sqrt{225-n} \) の値が整数となるような自然数 \( n \) の個数を求めなさい。
【解説】
\( \sqrt{225-n}=m \)(\( m \) は整数)として,両辺を2乗すると,
\( 225-n=m^2≧0 \) ・・・ ➀
また,\( n \) は自然数なので,
\( 225-n<225 \) ・・・ ➁
➀➁より,\( 225-n \) の値は,\( 0≦225-n≦225 \) の平方数になります。
\( 0≦225-n<225 \)
\( 0^2≦225-n<15^2 \)
なので,あてはまる \( n \) の値は,
\( 225-n=0 \; (=0^2) \) のとき → \( n=225 \)
\( 225-n=4 \; (=2^2) \) のとき → \( n=221 \)
\( 225-n=16 \; (=4^2) \) のとき → \( n=209 \)
\( 225-n=36 \; (=6^2) \) のとき → \( n=189 \)
\( 225-n=64 \; (=8^2) \) のとき → \( n=161 \)
\( 225-n=100 \; (=10^2) \) のとき → \( n=125 \)
\( 225-n=144 \; (=12^2) \) のとき → \( n=81 \)
\( 225-n=196 \; (=14^2) \) のとき → \( n=29 \)
\( 225-n=1 \; (=1^2) \) のとき → \( n=224 \)
\( 225-n=9 \; (=3^2) \) のとき → \( n=216 \)
\( 225-n=25 \; (=5^2) \) のとき → \( n=200 \)
\( 225-n=49 \; (=7^2) \) のとき → \( n=176 \)
\( 225-n=81 \; (=9^2) \) のとき → \( n=144 \)
\( 225-n=121 \; (=11^2) \) のとき → \( n=104 \)
\( 225-n=169 \; (=13^2) \) のとき → \( n=56 \)
であり,全部で \( 15 \) 個あります。
よって,\( \sqrt{225-n} \) の値が整数となるような自然数 \( n \) の個数は \( 15 \) 個になります。
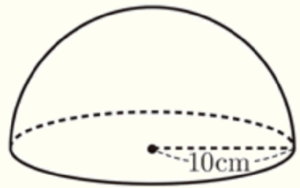
4 右の図の立体は,半径が \( 10 \; cm \) の半球である。この立体の表面積を求めなさい。
なお,円周率は \( \pi{} \) とする。
【解答】
\( 300\pi{} \; cm^2 \)
【解説】
【曲面部分の面積】
\( 4\pi{} \times 10^2 \times \dfrac{1}{2}=200\pi{} \; (cm^2) \)
【底面部分の面積】
\( \pi{} \times 10^2=100\pi{} \; (cm^2) \)
なので,この立体の表面積は,
\( 200\pi{}+100\pi{}=300\pi{} \; (cm^2) \)
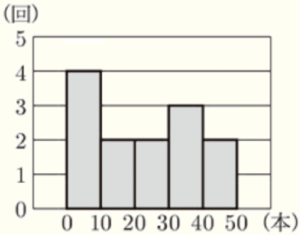
5 右の図は,ある野球選手が1年間に打ったホームランの本数の13年分の記録を,ヒストグラムに表したものである。このヒストグラムから,たとえば,記録が \( 0 \) 本以上 \( 10 \) 本未満の階級に入る年は \( 4 \) 回であることがわかる。
このヒストグラムをつくるのにもとにした記録を,箱ひげ図に表したものとして最も適切なものを,次のア~オから1つ選び,記号で答えなさい。
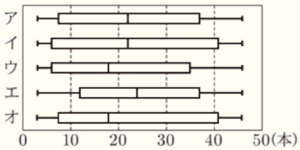
【解説】
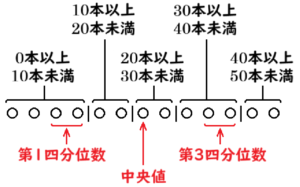
すべてのデータの数が13個なので,データの値を小さい順に並べ替えたとき,
中央値 ・・・ 小さい方から7番目の値
第一四分位数 ・・・ 小さい方から3番目と4番目の平均値
第三四分位数 ・・・ 小さい方から10番目と11番目の平均値
になります。
ヒストグラムから,
第一四分位数 ・・・ \( 0 \) 本以上 \( 10 \) 本未満の階級
中央値 ・・・ \( 20 \) 本以上 \( 30 \) 本未満の階級
第三四分位数 ・・・ \( 30 \) 本以上 \( 40 \) 本未満の階級
に含まれており,これらをすべて満たす箱ひげ図は ア になります。
大問2
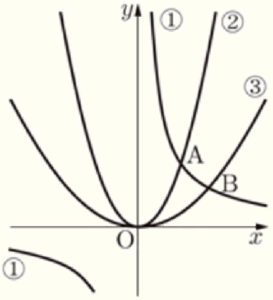
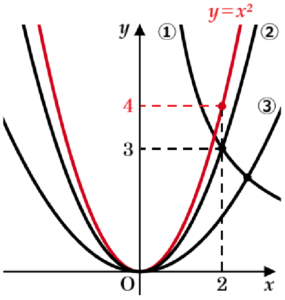
1 右の図において,➀は関数 \( y=\dfrac{6}{x} \) のグラフ,➁は関数 \( y=ax^2 \) のグラフ,➂は関数 \( y=bx^2 \) のグラフである。
➀と➁,➂との交点を,それぞれ \( A,B \) とする。点 \( A \) の \( x \) 座標が \( 2 \) で,点 \( B \) の \( x \) 座標が \( 2 \) より大きいとき,次の問いに答えなさい。
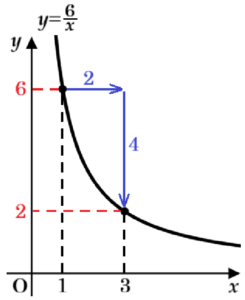
(1) 関数 \( y=\dfrac{6}{x} \) について,\( x \) の値が \( 1 \) から \( 3 \) まで増加するときの変化の割合を求めなさい。
【解説】
\( x \) の値が \( 1 \) のとき,\( y \) の値は
\( y=\dfrac{6}{1}=6 \)
\( x \) の値が \( 3 \) のとき,\( y \) の値は
\( y=\dfrac{6}{3}=2 \)
なので,変化の割合は,
\( \dfrac{2-6}{3-1}=-2 \)
(2) \( 1,a,b \) の関係を表す不等式として最も適切なものを,次のア~エから1つ選び,記号で答えなさい。
ア \( 1<a<b \) イ \( a<b<1 \) ウ \( b<1<a \) エ \( b<a<1 \)
【解説】
2次関数 \( y=mx^2 \)(\( m>0 \),\( m \) は定数) のグラフでは,\( m \) の値が大きくなるほど
グラフの開き具合は小さくなります。
\( y=ax^2 \) ・・・ ➁のグラフと \( y=bx^2 \) ・・・ ➂のグラフでは,
\( y=ax^2 \) ・・・ ➁の方がグラフの開き具合は小さいので,\( b<a \) であることがわかります。
点 \( A \) は,\( y=\dfrac{6}{x} \) ・・・ ➀上の点で,
\( x \) 座標が \( 2 \) なので,\( y \) 座標は
\( y=\dfrac{6}{2}=3 \)
また,関数 \( y=x^2 \) において,
\( x \) 座標が \( 2 \) なので,\( y \) 座標は
\( y=2^2=4 \)
なので,図の中に関数 \( y=x^2 \) のグラフを
書き加えると,右の図のようになります。
関数 \( y=x^2 \) のグラフの方が,➁のグラフより開き具合が小さいので,
\( a<1 \) であることがわかります。
以上より,\( 1,a,b \) の関係は エ \( b<a<1 \) になります。
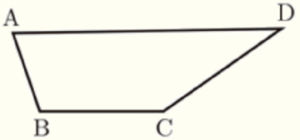
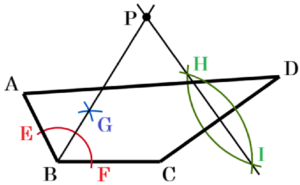
2 右の図のように,四角形 \( ABCD \) がある。下の【条件】の➀,➁をともにみたす点 \( P \) を,定規とコンパスを使って作図しなさい。
ただし,作図に使った線は残しておくこと。
【条件】
① 点 \( P \) は,直線 \( AB \) と直線 \( BC \) から等しい距離にあり,直線 \( BC \) の上側の点である。
② 線分 \( PC \) の長さは,線分 \( PD \) の長さと等しい。
【解答】
手順1 点 \( B \) を中心に円弧を描く
(辺 \( AB,BC \) との交点を \( E,F \) とします)
手順2 2点 \( E,F \) を中心に円弧を描く
(交点を \( G \) とします)
手順3 2点 \( B,G \) を通る直線を描く
手順4 2点 \( C,D \) を中心に円弧を描く
(交点を \( H,I \) とします)
手順5 2点 \( H,I \) を通る直線を描く
手順3と手順5の直線の交点が求める点 \( P \) になります。
【解説】
点 \( P \) が「条件➀ を満たすとき」と「条件➁ を満たすとき」をわけて考え,
その結果から,条件➀と➁の両方を満たす場所を考えます。
【条件➀ を満たすとき】
点 \( P \) が,直線 \( AB \) と直線 \( BC \) から
等しい距離にあるとき,
「点 \( P \) から直線 \( AB \) にひいた垂線の長さ」
と
「点 \( P \) から直線 \( BC \) にひいた垂線の長さ」
は等しくなります。
問題の図において,
点 \( P \) から直線 \( AB,BC \) に垂線をひき,
交点を \( S,T \) とすると,
\( △PBS≡△PBT \) であり,対応する角は等しい
ので,\( ∠PBA=∠PBC \) になっています。
\( \phantom{ } \)
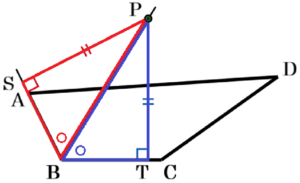
【\( △PBS≡△PBT \) である理由】
\( △PBS \) と \( △PBT \) において,
仮定より,\( PS=PT \) ・・・ ➀
仮定より,\( ∠PSB=∠PTB=90° \) ・・・ ➁
\( PB \) は共通 ・・・ ➂
➀➁➂より,
斜辺と他の1辺が等しい直角三角形なので,
\( △PBS≡△PBT \)
つまり,直線 \( BP \) は \( ∠ABC \) の二等分線であり,
点 \( P \) は,\( ∠ABC \) の二等分線上の点であるといえます。
【条件➁ を満たすとき】
線分 \( PC \) の長さが線分 \( PD \) の長さと等しいとき,
問題の図において,
点 \( P \) から直線 \( CD \) に垂線をひき,
交点を \( U \) とすると,
\( △PCU≡△PDU \) であり,対応する辺は等しい
ので,\( CU=DU \) になっています。
\( \phantom{ } \)
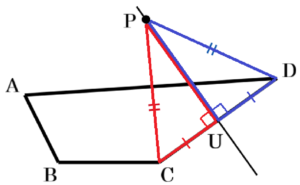
【\( △PCU≡△PDU \) である理由】
\( △PCU \) と \( △PDU \) において,
仮定より,\( PC=PD \) ・・・ ➀
仮定より,\( ∠PUC=∠PUD=90° \) ・・・ ➁
\( PU \) は共通 ・・・ ➂
➀➁➂より,
斜辺と他の1辺が等しい直角三角形なので,
\( △PCU≡△PDU \)
つまり,点 \( U \) は線分 \( CD \) の中点であり,
点 \( P \) は,線分 \( CD \) の垂直二等分線上の点であるといえます。
以上より,点 \( P \) は,\( ∠ABC \) の二等分線と線分 \( CD \) の垂直二等分線の交点になります。
3 次の問題について,あとの問いに答えなさい。
[問題]
そば粉と小麦粉が,それぞれ \( 3000 \; g \) ずつあります。右の表は,そばとうどんを,それぞれ \( 5 \) 人分作るために必要なそば粉と小麦粉の量を示したものです。この表をもとにして,そばとうどんを合わせて \( 58 \) 人分作ったところ,すべての小麦粉を使いましたが,そば粉は残りました。残ったそば粉の量は何 \( g \) ですか。
\( \phantom{ } \)

(1) この問題を解くのに,方程式を利用することが考えられる。どの数量を文字で表すかを示し,問題にふくまれる数量の関係から,1次方程式または連立方程式のいずれかをつくりなさい。
【解答】
【1次方程式で表す場合】
そばを \( x \) 人分作ったとすると,
\( \dfrac{100}{5}x+\dfrac{500}{5}(58-x)=3000 \)
【連立方程式で表す場合】
そばを \( x \) 人分,うどんを \( y \) 人分作ったとすると,
\( \left\{ \begin{array}{}
x+y=58 \\
\dfrac{100}{5}x+\dfrac{500}{5}y=3000 \\
\end{array} \right. \)
【解説】
【1次方程式で表す場合】
そばを \( x \) 人分作ったとすると,そばとうどんを合わせて \( 58 \) 人分作ったことから,
作ったうどんの量は \( (58-x) \) 人分と表すことができます。
\( 5 \) 人分のそばをつくるために,必要な小麦粉の量は,\( 100 \; g \) なので,
\( 1 \) 人分のそばをつくるために,必要な小麦粉の量は,\( \dfrac{100}{5} \; g \) であり,
\( x \) 人分のそばをつくるために,必要な小麦粉の量は,\( \dfrac{100}{5}x \; g \)
\( 5 \) 人分のうどんをつくるために,必要な小麦粉の量は,\( 500 \; g \) なので,
\( 1 \) 人分のうどんをつくるために,必要な小麦粉の量は,\( \dfrac{500}{5} \; g \)
\( (58-x) \) 人分のうどんをつくるために,必要な小麦粉の量は,\( \dfrac{500}{5}(58-x) \; g \)
と表すことができます。
そばとうどんを合わせて \( 58 \) 人分作るために使った小麦粉の量は \( 3000 \; g \) なので,
この関係を方程式で表すと,
\( \dfrac{100}{5}x+\dfrac{500}{5}(58-x)=3000 \)
【連立方程式で表す場合】
そばを \( x \) 人分,うどんを \( y \) 人分作ったとすると,
そばとうどんを合わせて \( 58 \) 人分作ったので,この関係を方程式で表すと,
\( x+y=58 \) ・・・ ➀
\( x \) 人分のそばと \( y \) 人分のうどんを作るために必要な小麦粉の量に注目すると,
\( 5 \) 人分のそばをつくるために,必要な小麦粉の量は,\( 100 \; g \) なので,
\( 1 \) 人分のそばをつくるために,必要な小麦粉の量は,\( \dfrac{100}{5} \; g \) であり,
\( x \) 人分のそばをつくるために,必要な小麦粉の量は,\( \dfrac{100}{5}x \; g \)
\( 5 \) 人分のうどんをつくるために,必要な小麦粉の量は,\( 500 \; g \) なので,
\( 1 \) 人分のうどんをつくるために,必要な小麦粉の量は,\( \dfrac{500}{5} \; g \)
\( y \) 人分のうどんをつくるために,必要な小麦粉の量は,\( \dfrac{500}{5}y \; g \)
と表すことができます。
\( x \) 人分のそばと \( y \) 人分のうどんを作るために使った小麦粉の量は \( 3000 \; g \) なので,
この関係を方程式で表すと,
\( \dfrac{100}{5}x+\dfrac{500}{5}y=3000 \) ・・・ ➁
➀➁を連立方程式として表すと,
\( \left\{ \begin{array}{}
x+y=58 \\
\dfrac{100}{5}x+\dfrac{500}{5}y=3000 \\
\end{array} \right. \)
(2) 残ったそば粉の量を求めなさい。
【解説】
【(1)を1次方程式で表した場合】
\( \dfrac{100}{5}x+\dfrac{500}{5}(58-x)=3000 \)
\( 20x+100(58-x)=3000 \)
\( x+5(58-x)=150 \)
\( -4x+290=150 \)
\( 4x=140 \)
\( x=35 \)(人)
\( 35 \) 人分のそばを作るために使ったそば粉の量は
\( \dfrac{400}{5} \times 35=2800 \; (g) \)
なので,残ったそば粉の量は
\( 3000-2800=200 \; (g) \)
【(1)を連立方程式で表した場合】
\( \left\{ \begin{array}{}
x+y=58 \;\; ・・・ \;\; ➀ \\
\dfrac{100}{5}x+\dfrac{500}{5}y=3000 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁より,
\( x+5y=150 \) ・・・ ➁’
➁’-➀ すると,
\( 4y=92 \)
\( y=23 \)(人)
➀ の代入すると,
\( x+23=58 \)
\( x=35 \)(人)
\( 35 \) 人分のそばを作るために使ったそば粉の量は
\( \dfrac{400}{5} \times 35=2800 \; (g) \) なので,
残ったそば粉の量は
\( 3000-2800=200 \; (g) \)
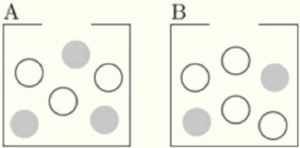
4 右の図のように,Aの箱の中には,赤玉 \( 3 \) 個と白玉 \( 3 \) 個,Bの箱の中には,赤玉 \( 2 \) 個と白玉 \( 4 \) 個が,それぞれ入っている。
Aの箱から \( 1 \) 個の玉を取り出し,赤玉が出ると景品をもらえるゲームSと,Bの箱から \( 2 \) 個の玉を同時に取り出し,少なくとも \( 1 \) 個は赤玉が出ると景品をもらえるゲームTの,2つのゲームがある。このとき,景品をもらいやすいのは,ゲームSとゲームTのどちらであるかを,確率を使って説明しなさい。
ただし,それぞれの箱において,どの玉が取り出されることも同様に確からしいものとする。
【解答】
ゲームSで景品をもらえる確率は \( \dfrac{1}{2} \),ゲームTで景品をもらえる確率は \( \dfrac{3}{5} \) で,
ゲームTで景品をもらえる確率の方が高い。
よって,ゲームTの方が景品をもらいやすい。
【解説】
【ゲームSで景品をもらえる確率】
\( 3 \) 個の赤玉に「赤1」,「赤2」,「赤3」
\( 3 \) 個の白玉に「白1」,「白2」,「白3」
と名前をつけると,赤玉が出るのは,
「赤1」を選んだとき,「赤2」を選んだとき,「赤3」を選んだとき,
の \( 3 \) 通り,すべての組み合わせは \( 6 \) 通りなので,
景品をもらえる確率は,\( \dfrac{3}{6}=\dfrac{1}{2} \)
【ゲームTで景品をもらえる確率】
\( 2 \) 個のうち,少なくとも \( 1 \) 個は赤玉のとき景品がもらえるのだから,
景品がもらえないのは,赤玉が出ない(2個とも白玉が出る)場合です。
\( 2 \) 個の赤玉に「赤1」,「赤2」
\( 3 \) 個の白玉に「白1」,「白2」,「白3」,「白4」
と名前をつけ,取り出した \( 2 \) 個の玉の組み合わせを樹形図に書き出すと,
2個とも白玉が出る組み合わせは,\( 6 \) 通り,
すべての組み合わせは \( 15 \) 通りなので,
景品をもらえない確率は,\( \dfrac{6}{15}=\dfrac{2}{5} \) です。
よって,景品をもらえる確率は,\( 1-\dfrac{2}{5}=\dfrac{3}{5} \) です。

大問3
A駅とB駅を結ぶロープウェイと,B駅とC駅を結ぶロープウェイがあり,A駅,B駅,C駅がある地点の標高は,それぞれ \( 100 \; m,550 \; m,900 \; m \) である。ある日,明美さんは,ロープウェイを利用して,A駅からB駅に向かい,A駅を出発してから \( 6 \) 分後にB駅に到着した。B駅で \( 3 \) 分間待ったあと,B駅からC駅に向かうロープウェイを利用したところ,明美さんが,C駅に到着したのは,A駅を出発してから \( 19 \) 分後だった。このとき,それぞれの問いに答えなさい。
ただし,明美さんが,A駅を出発してからB駅に到着するまでの間と,B駅を出発してからC駅に到着するまでの間,明美さんがいる位置の標高は,それぞれ一定の割合で変化するものとする。
1 明美さんがA駅を出発してから \( x \) 分後の,明美さんがいる位置の標高を \( y \; m \) とする。明美さんがA駅を出発してから,B駅に到着するまでの \( x \) と \( y \) の関係をグラフに表したところ,図のようになった。次の問いに答えなさい。
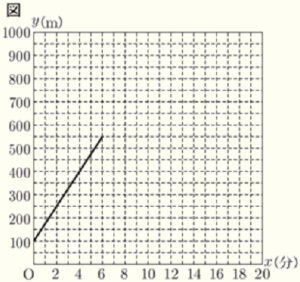
(1) 明美さんがA駅を出発してから \( 2 \) 分後の,明美さんがいる位置の標高は何 \( m \) か,答えなさい。
【解説】
グラフより,A駅を出発してから \( 6 \) 分間に \( 550-100=450 \; (m) \) 標高が高くなっているので,
\( 1 \) 分あたり \( \dfrac{450}{6}=75 \; (m) \) ずつ標高が高くなっていることになります。
ここから,\( 2 \) 分間で \( 75 \times 2=150 \; (m) \) 標高が高くなったとわかります。
スタートのA駅の標高は \( 100 \; m \) なので,出発してから \( 2 \) 分後の標高は
\( 100+150=250 \; (m) \)
になります。
(2) 表は,明美さんがA駅を出発してからC駅に到着するまでの \( x \) と \( y \) の関係を式に表したものである。 \( \boxed{ ア } \) ~ \( \boxed{ ウ } \) にあてはまる数または式を,それぞれ書きなさい。
また,このときの \( x \) と \( y \) の関係を表すグラフを,図にかき加えなさい。
【解答】
\( \boxed{ ア } \) ・・・ \( 75x+100 \)
\( \boxed{ イ } \) ・・・ \( 9 \)
\( \boxed{ ウ } \) ・・・ \( 35x+235 \)
グラフ
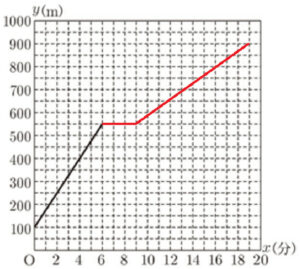
【解説】
\( \boxed{ ア } \)
グラフより, \( 0≦x≦6 \) の直線は \( (0,100),(6,550) \) を通っているので,
傾き \( =\dfrac{550-100}{6-0}=75 \)
であり,この直線の式は \( y=75x+100 \) になります。
\( \boxed{ イ } \)
\( y=550 \) の式は,B駅から移動していないことを表しています。
明美さんがB駅に到着したのは,A駅を出発してから \( 6 \) 分後なので,
明美さんがB駅を出発したのは,A駅を出発してから \( 6+3=9 \) 分後になります。
\( \boxed{ ウ } \)
明美さんがB駅を出発した時間と場所を表す座標は \( (9,550) \),
明美さんがC駅に到着した時間と場所を表す座標は \( (19,900) \)
なので,この2点を通る直線の式を \( y=ax+b \) とすると,
\( a=\dfrac{900-550}{19-9}=35 \)
\( y=35x+b \) に \( x=9,y=550 \) を代入すると,
\( 550=35 \times 9+b \)
\( b=235 \)
なので,求める直線の式は \( y=35x+235 \) になります。
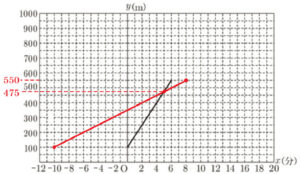
2 大樹さんは,同じ日に,バスを利用して,明美さんより早くA駅を出発してB駅に向かった。すると,明美さんがA駅を出発した \( 5 \) 分後に,大樹さんと明美さんがいる位置の標高が等しくなった。また,大樹さんは,明美さんがB駅に到着した \( 2 \) 分後にB駅に到着した。大樹さんがA駅を出発したのは,明美さんがA駅を出発する何分前か,求めなさい。
ただし,大樹さんが,A駅を出発してからB駅到着するまでの間,大樹さんがいる位置の標高は,一定の割合で変化するものとする。
【解説】
\( x=5 \) のときの \( y \) 座標の値は,
\( y=75 \times 5+100=475 \)
なので,大樹さんと明美さんがいる位置の標高が等しくなったのは \( (5,475) \) のときです。
また,大樹さんがB駅に到着したのは \( (8,550) \) のときなので,
この2点を通る直線の式を \( y=mx+n \) とすると,
\( m=\dfrac{550-475}{8-5}=25 \)
\( y=25x+n \) に \( x=8,y=550 \) を代入すると,
\( 550=25 \times 8+b \)
\( b=350 \)
なので,この直線の式は \( y=25x+350 \) になります。
大樹さんがA駅を出発した点を表しているのは \( y=100 \) になる点なので,
\( y=25x+350 \) に \( y=100 \) を代入すると,
\( 100=25x+350 \)
\( x=-10 \)
よって,大樹さんがA駅を出発したのは,明美さんがA駅を出発する \( 10 \) 分前になります。
大問4
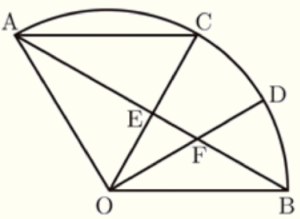
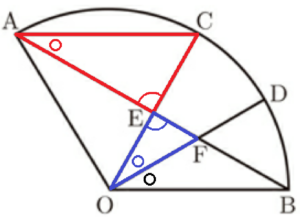
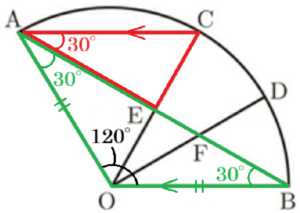
右の図のように,線分 \( OA,OB \) を半径とし,中心角の大きさが \( 180° \) より小さいおうぎ形 \( OAB \) がある。2点 \( A,B \) とは異なる点 \( C \) を,弧 \( AB \) 上にとり,点 \( A \) と \( C \) を結ぶ。また,点 \( D \) を,弧 \( BC \) 上に,\( ∠BOD=∠COD \) となるようにとる。線分 \( AB \) と線分 \( OC,OD \) との交点をそれぞれ \( E,F \) とする。このとき,次の問いに答えなさい。
1 \( △AEC \) ∽ \( △OEF \) であることを証明しなさい。
【解答】
\( △AEC \) と \( △OEF \) において,
対頂角は等しいので,\( ∠AEC=∠OEF \) ・・・ ➀
\( ∠EAC \) は弧 \( BC \) に対する円周角,
\( ∠BOC \) は弧 \( BC \) に対する中心角なので,
\( ∠EAC=\dfrac{1}{2}∠BOC \) ・・・ ➁
仮定より,\( ∠EOF=\dfrac{1}{2}∠BOC \) ・・・ ➂
➁➂より,\( ∠EAC=∠EOF \) ・・・ ➃
➀➃より,2組の角がそれぞれ等しいので,
\( △AEC \) ∽ \( △OEF \)
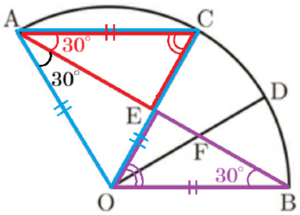
2 \( OA=6cm,∠AOB=120°,AC//OB \) であるとき,次の問いに答えなさい。
(1) \( △AEC \) と \( △OBF \) の面積の比を求めなさい。
【解説】
\( △OBF=△BEO-△OEF \) と考えると,図から \( △AEC≡△OEF \) であれば,
\( △AEC \) と \( △OEF \) の相似比を求めることで,
\( △AEC \) と \( △OBF \) の面積の比を求めることができると推測できます。
\( △AEC≡△OEF \) であることを確認する
\( OA=OB,∠AOB=120° \) より,
\( ∠OAB=∠OBA=30° \)
\( AC//OB \) より,錯角は等しいので,
\( ∠EAC=∠OBA=30° \)
になっています。
\( \phantom{ } \)
このとき,\( OA=OC,∠OAC=60° \) より,
\( △OAC \) は内角の1つが \( 60° \) の
二等辺三角形なので,正三角形になっており,
\( ∠EAC=∠EBO \)
\( ∠ECA=∠EOB \)
\( AC=BO \)
より,\( △AEC≡△OEF \) になっています。
\( \phantom{ } \)
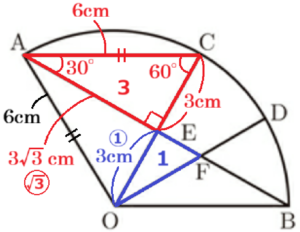
\( △AEC \) と \( △OEF \) の相似比を求める
1より,\( △AEC \) ∽ \( △OEF \) であり,
\( △OAC \) が正三角形であることから,
\( AC=OC=OA=6 \; cm \)
\( ∠CAE=30°,∠ACE=60° \) より,
\( △AEC \) は \( 30°,60°,90° \) の直角三角形になっているので,
\( AE=\dfrac{\sqrt{3}}{2}AC=3\sqrt{3} \; (cm) \)
\( CE=\dfrac{1}{2}AC=3 \; (cm) \)
\( \phantom{ } \)
\( OE=OC-CE=3 \; cm \) であることから,\( △AEC \) と \( △OEF \) の相似比は,
\( AE:OE=3\sqrt{3}:3=\sqrt{3}:1 \)
相似な三角形の面積は相似比の2乗の比と等しいので,
\( △AEC:△OEF=(\sqrt{3})^2:1^2=3:1 \)
よって,\( △AEC \) と \( △OBF \) の面積の比は,
\( △AEC:△OBF=△AEC:(△BEO-△OEF) \)
\( =△AEC:(△AEC-△OEF) \)
\( =3:(3-1) \)
\( =3:2 \)
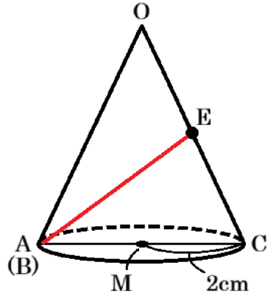
(2) 線分 \( OA \) と \( OB \) を合わせて円すいの側面にあたる部分をつくったときの,2点 \( A,E \) 間の距離を求めなさい。
【解答】
\( \sqrt{17} \; cm \)
【解説】
つくった円すいはどのような形なのか?
\( ∠AOB=120°,∠AOC=60° \) より,\( ∠BOC=60° \) であり,
弧の長さは,中心角の大きさに比例するので,
\( \stackrel{\huge\frown}{ AC }=\stackrel{\huge\frown}{ CB } \) になっています。
\( \phantom{ } \)
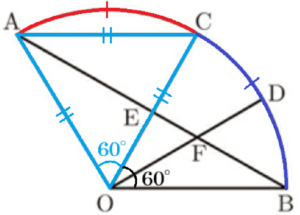
このおうぎ形を組み立てて円すいをつくったとき,
底面の円周の長さは \( \stackrel{\huge\frown}{ AB } \) の長さと等しいので,
\( \stackrel{\huge\frown}{ AC } \left( \stackrel{\huge\frown}{ CB } \right) \) は底面の円の半周分であり,
底面は \( AC \) を直径とする円になります。
おうぎ形 \( OAB \) の \( \stackrel{\huge\frown}{ AB } \) の長さは,
\( 2\pi{} \times 6 \times \dfrac{120°}{360°}=4\pi{} \; (cm) \)
なので,底面の半径を \( r \; cm \) とすると,
\( 2\pi{}r=4\pi{} \)
\( r=2 \; (cm) \)
また,(1)より \( CE=3 \; cm \) なので,
つくった円すいは右の図のようになります。
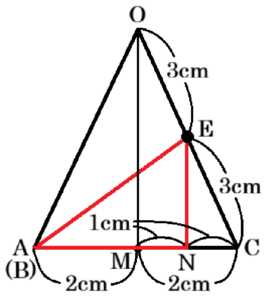
線分 \( AE \) の長さを求める
この円すいにおいて,面 \( OAC \) に注目します。
底面の円の中心を \( M \),点 \( E \) から底面に垂線をひいた交点を \( N \) とすると,\( OE=CE=3 \; cm \) なので,
\( △OCM \) と \( △ECN \) は相似であり,
相似比は \( 2:1 \) になっています。
相似な三角形の対応する辺の比は等しいので,
\( CM:CN=2:1 \) であり,\( CN=1 \; cm \) です。
\( △ECN \) において,三平方の定理より,
\( EN^2=3^2-1^2=8 \)
\( △AEN \) において,三平方の定理より,
\( AE^2=AN^2+EN^2 \)
\( =3^2+8 \)
\( =17 \)
\( AE=\sqrt{17} \; (cm) \)