大問1
(1) \( (-2)+6 \) を計算しなさい。
(2) \( 5a+1-(2-3a) \) を計算しなさい。
【解説】
\( =5a+1-2+3a \)
\( =8a-1 \)
(3) \( \dfrac{2}{5}a \times \left( -\dfrac{10}{9}b \right) \) を計算しなさい。
【解答】
\( -\dfrac{4ab}{9} \) または \( -\dfrac{4}{9}ab \)
【解説】
\( =-\dfrac{2a \times 10b}{5 \times 9} \)
\( =-\dfrac{4ab}{9} \)
\( \left( =-\dfrac{4}{9}ab \right) \)
(4) \( (8x^2-6xy) \div 2x \) を計算しなさい。
【解説】
\( =\dfrac{8x^2-6xy}{2x} \)
\( =4x-3y \)
(5) \( (\sqrt{7}+3)(\sqrt{7}-3) \) を計算しなさい。
【解説】
\( =(\sqrt{7})^2-3^2 \)
\( =7-9 \)
\( =-2 \)
大問2
(1) \( x^2-5x-24 \) を因数分解しなさい。
【解説】
\( =x^2+\{3+(-8)\}x+\{3 \times (-8)\} \)
\( =(x+3)(x-8) \)
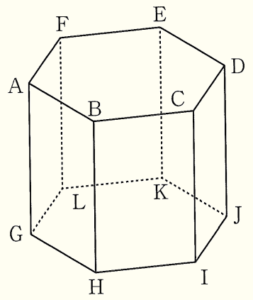
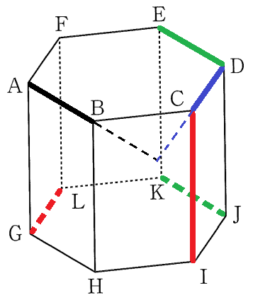
(2) 右の図の正六角柱 \( ABCDEF-GHIJKL \) において, 辺 \( AB \) とねじれの位置の関係にある辺を,次のア~オから2つ選び,記号で答えなさい。
ア 辺 \( CD \) イ 辺 \( CI \) ウ 辺 \( DE \)
エ 辺 \( GL \) オ 辺 \( JK \)
【解答】
イ 辺 \( CI \)
エ 辺 \( GL \)
【解説】
ねじれの位置の関係にある辺とは,
どこまで延ばしても交わらない辺のうち,平行ではないもの
のことをいいます。
ア 辺 \( CD \)
辺 \( AB \) と辺 \( CD \) を延長すると,交わります。
ウ 辺 \( DE \),オ 辺 \( JK \)
辺 \( AB \) と平行になっています。
(3) 次の図は,ある年における,総人口がともに130万人である自治体Aと自治体Bの年齢別人口のデータを,箱ひげ図に表したものである。
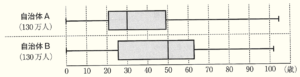
この箱ひげ図から読み取れることとして正しいものを,次のア~エから1つ選び,記号で答えなさい。
ア 自治体Aの平均年齢は30歳である。
イ 四分位範囲は,自治体Bより自治体Aの方が大きい。
ウ 50歳以下の人口は,自治体Bより自治体Aの方が多い。
エ 自治体Aの60歳以上の人口は,自治体Bの80歳以上の人口の2倍である。
【解説】
【正しい理由】
箱ひげ図のひげの部分と2つに分けられた箱のそれぞれの部分には,
全体の約25%にあたる個数のデータが含まれています。

自治体A ・・・ 第三四分位数が約49歳なので,50歳以下の人口は,
\( 130 \) 万 \( \times 0.75=97 \) 万 \( 5 \) 千人以上いるとわかります。
自治体B ・・・ 中央値が50歳なので,50歳以下の人口は,65万人未満とわかります。
よって,50歳以下の人口は,自治体Bより自治体Aの方が多くなっています。
【正しくない理由】
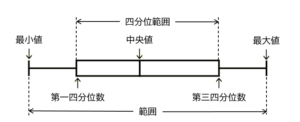
ア ・・・ 箱ひげ図から,自治体Aの中央値が30歳であることがわかりますが,
中央値と平均値は等しくなるとは限りません。
イ ・・・ 四分位範囲は 第三四分位数 \( – \) 第一四分位数 で求められます。
自治体Aのおよその四分位範囲は \( 49-21=28 \)(歳)
自治体Bのおよその四分位範囲は \( 63-25=38 \)(歳)
自治体Bの方が自治体Aより大きくなっています。
エ ・・・ 箱ひげ図のひげの部分には全体の約25%にあたる個数のデータが含まれるので,
自治体Aの60歳以上の人口と自治体Bの80歳以上の人口は,
どちらも32万5千人未満であると考えられますが,
その約32万5千人の内訳は,箱ひげ図からだけでは判断できません。
(自治体Aの場合,50歳以上60歳未満の人が約32万人いるかもしれないし,
90歳以上100歳未満の人が約32万人いるかもしれない)
つまり,この箱ひげ図からだけでは,自治体Aの60歳以上の人口と自治体Bの80歳以上の人口
を比較することはできません。
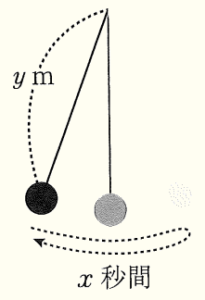
(4) 1往復するのに \( x \) 秒かかるふりこの長さを \( y \; m \) とすると,\( x \) と \( y \) の間には,\( y=\dfrac{1}{4}x^2 \) という関係がある。1往復するのに \( 6 \) 秒かかるふりこの長さは何 \( m \) か求めなさい。
【解説】
\( y=\dfrac{1}{4}x^2 \) に \( x=6 \) を代入すると,
\( y=\dfrac{1}{4} \times 6^2=9 \; (m) \)
大問3
関数 \( y=\dfrac{a}{x} \) が表す双曲線 ①について, 次の(1),(2)に答えなさい。
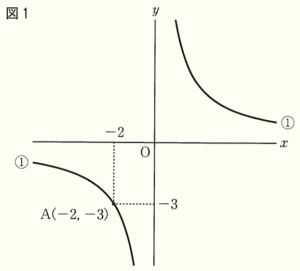
(1) 図1のように,点 \( A(-2,-3) \) は双曲線①上の点である。このとき,\( a \) の値を求めなさい。
【解説】
\( y=\dfrac{a}{x} \) に \( x=-2,y=-3 \) を代入すると,
\( -3=\dfrac{a}{-2} \)
\( a=6 \)
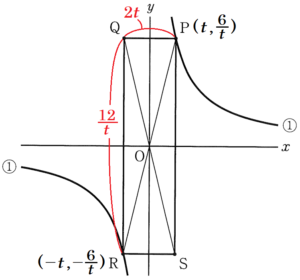
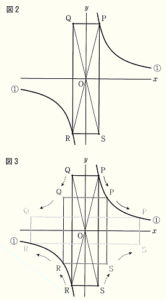
(2) 点 \( P \) は双曲線 ① 上にあり,図2のように,長方形 \( PQRS \) を,対角線の交点が原点 \( O \) となり,辺 \( PQ \) が \( x \) 軸と平行になるようにつくる。点 \( P \) の \( x \) 座標が増加すると,点 \( P \) は図3の矢印 (→)の方向に動き,それに対応して,点 \( Q,R,S \) は長方形 \( PQRS \) の対角線の交点が原点 \( O \) となることを維持しながら矢印 (→) の方向に動く。
このとき,長方形 \( PQRS \) の面積はどのように変化するか, 正しいものを,次のア~オから1つ選び,記号で答えなさい。
ア 増加し続ける
イ 減少し続ける
ウ 一定である
エ 増加したのち, 減少し続ける
オ 減少したのち, 増加し続ける
【解説】
点 \( P \) の \( x \) 座標を \( t \) とすると,
点 \( P \) の座標は \( P \left( t,\dfrac{6}{t} \right) \) と表すことができます。
長方形の対角線はそれぞれの中点で交わるので,
点 \( R \) の座標は \( R \left(-t,-\dfrac{6}{t} \right) \) と表すことができます。
このとき,辺 \( PQ \) が \( x \) 軸と平行になることから,
辺 \( QR \) は \( x \) 軸と垂直になり,
点 \( Q \) の座標は \( Q \left( -t,\dfrac{6}{t} \right) \) と表すことができます。
ここから,
\( PQ=2t,QR=\dfrac{12}{t} \)
と表すことができるので,
長方形 \( PQRS \) の面積は
\( \dfrac{12}{t} \times 2t=24 \)
よって,長方形 \( PQRS \) の面積は,\( t \) の値に寄らず常に \( 24 \) で一定になります。
大問4
全校生徒数が \( 871 \) 人の中学校で,保健委員会が学校新聞の記事を作成している。保健委員会は,生徒のインターネットの利用実態を調査するために,【アンケート】を実施することにした。次の【アンケート】は,保健委員会が作成したものの一部である。このとき,下の(1),(2)に答えなさい。

(1) 全校生徒 \( 871 \) 人から \( 120 \) 人を無作為に抽出して,この【アンケート】を実施したところ,全員が回答し,\( Q \, 1 \) で「イ 1時間以上,2時間未満」と回答した生徒は \( 48 \) 人であった。
この結果から考えると,先週1週間における,1日あたりのインターネット平均利用時間が「1時間以上,2時間未満」である生徒は,全校生徒 \( 871 \) 人のうち,およそ何人と推定されるか。小数第1位を四捨五入した概数で答えなさい。
【解説】
母集団に含まれる調査対象の割合(比)は,標本に含まれる調査対象の割合(比)と等しくなる
と考えられます。
母集団 ・・・ 全校生徒 \( 871 \) 人
母集団に含まれる調査対象 ・・・ 利用時間が「1時間以上,2時間未満」である生徒 \( x \) 人
標本 ・・・【アンケート】に回答した生徒 \( 120 \) 人
標本に含まれる調査対象 ・・・ 【アンケート】で「イ 1時間以上,2時間未満」と回答した生徒 \( 48 \) 人
となるので,
\( 871:x=120:48 \)
\( 871:x=5:2 \)
\( 5x=1742 \)
\( x=348.4 \)
小数第1位を四捨五入すると,\( 348.4 → 348 \)(人)
(2) 保健委員会のAさん,Bさん,Cさんは【アンケート】の回答を集計したグラフと,集計結果を分析した文章を学校新聞の記事に載せるために,グラフ作成の担当者1人と文章作成の担当者2人を以下の【方法】で決めることにした。
【方法】
【手順】
1枚の硬貨を,Aさん,Bさん,Cさんが順番に1回ずつ投げる。
【担当決定のルール】
3人が1回ずつ投げた硬貨の表裏の出かたのうち
・ 1人が表,2人が裏の場合 → 表が出た人がグラフ担当,裏が出た人が文章担当
・ 1人が裏,2人が表の場合 → 裏が出た人がグラフ担当,表が出た人が文章担当
・ 全員が表の場合 → Cさんがグラフ担当, AさんとBさんが文章担当
・ 全員が裏の場合 → Bさんがグラフ担当, AさんとCさんが文章担当
上の【方法】で担当を決めるとき,AさんとCさんのどちらがグラフ担当になりやすいか。確率を求めるまでの過程を明らかにして説明しなさい。
【解答】
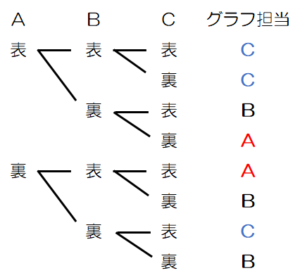
Aさん,Bさん,Cさんが順番に1回ずつ硬貨を
投げたときの表裏の組み合わせとそれぞれの場合に
おけるグラフ担当者を右の図のように樹形図に表すと,
すべての組み合わせは \( 8 \) 通り,
Aさんがグラフ担当になる組み合わせは \( 2 \) 通り
Cさんがグラフ担当になる組み合わせは \( 3 \) 通り
なので,
Aさんがグラフ担当になる確率は \( \dfrac{2}{8}=\dfrac{1}{4} \)
Cさんがグラフ担当になる確率は \( \dfrac{3}{8} \)
で,Cさんがグラフ担当になる確率の方が高い。
よって,Cさんの方がグラフ担当になりやすい。
大問5
Sさんは花植えボランティアに参加した。次の(1),(2)に答えなさい。
(1) Sさんは長方形の花だんから正方形の花だんへの花の植え替えを手伝った。長方形の花だんは,横の長さが縦の長さの4倍であり,周の長さは \( 30 \; m \) であった。長方形の花だんの面積が正方形の花だんの面積と同じとき,正方形の花だんの1辺の長さを求めなさい。

【解説】
長方形の花だんの縦の長さを \( x \; m \) とすると,横の長さは \( 4x \; m \) と表すことができます。
このとき,周の長さは \( 30 \; m \) なので,
\( 2(x+4x)=30 \)
\( x+4x=15 \)
\( x=3 \; (m) \)
ここから,縦の長さは \( 3 \; m \),横の長さは \( 12 \; m \) なので,
長方形の花だんの面積は \( 36 \; m^2 \) とわかります。
正方形の花だんの面積も \( 36 \; m^2 \) なので,1辺の長さは \( 6 \; m \) になります。
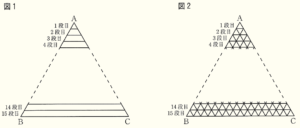
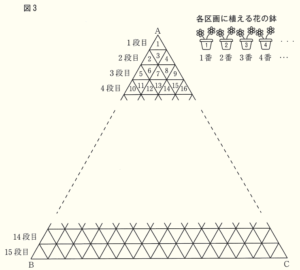
(2) 次に,Sさんは三角形の花だんの花植え作業を手伝った。三角形の花だんの花植え作業は,三角形の花だんを \( △ABC \) とし,【手順1】から【手順4】により行う。図1から図3は【手順1】から【手順4】の様子を図にしたものである。
【手順1】 辺 \( AB \) と辺 \( AC \) を \( 15 \) 等分する点をそれぞれとり,辺 \( BC \) に平行になるように \( 15 \) 等分
した点をそれぞれ結ぶ。図1のように区分けされた場所を,頂点 \( A \) から辺 \( BC \) に向かって
\( 1 \) 段目,\( 2 \) 段目,・・・,\( 15 \) 段目とする。
【手順2】 辺 \( BC \) を \( 15 \) 等分する点をとり,辺 \( AB \) と平行になるように辺 \( AC \) を \( 15 \) 等分した点と
それぞれ結ぶ。辺 \( BC \) を \( 15 \) 等分した点と辺 \( AB \) を \( 15 \) 等分した点を辺 \( AC \) と平行と
なるようにそれぞれ結び, \( △ABC \) を図2のように三角形の区画に分割する。
【手順3】 図3のように,分割した三角形の区画すべてに,以下の規則で \( 1 \) から順に自然数の番号を
付ける。
① \( 1 \) 段目を \( 1 \) とする。
② \( 2 \) 段目の左端を \( 2 \) とし,左から順に番号を付ける。
③ \( 3 \) 段目以降の段は,その段の1つ上の段の右端の番号に \( 1 \) を足したものを,その段の
左端の番号とし,左から順に番号を付けていく。
④ ③の操作を \( 3 \) 段目から順に \( 15 \) 段目までおこなっていく。
【手順4】 図3のように,各区画に植える花の鉢には \( 1 \) から順に自然数の番号が付いており,番号を
付けた区画に同じ番号の鉢の花を植える。
Sさんは,\( 10 \) 段目のすべての区画に花を植えることになった。
このとき,次の文の ア , イ にあてはまる数を求めなさい。
Sさんは ア 番から イ 番までの鉢の花を植える。
【解答】
ア ・・・ \( 82 \)
イ ・・・ \( 100 \)
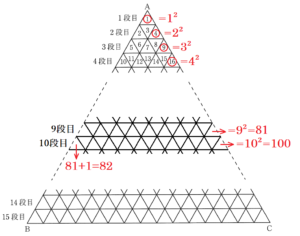
【解説】
各段の右端の番号に注目すると,
1段目 ・・・ \( 1=1^2 \)
2段目 ・・・ \( 4=2^2 \)
3段目 ・・・ \( 9=3^2 \)
4段目 ・・・ \( 16=4^2 \)
となっており,
9段目の右端の番号は \( 9^2=81 \)
10段目の右端の番号は \( 10^2=100 \)
になることがわかります。
また,10段目の左端の番号は,
9段目の右端の番号 \( 9^2=81 \) の次の番号なので,\( 82 \) になります。
大問6
直角三角形について,次の(1)~(3)に答えなさい。
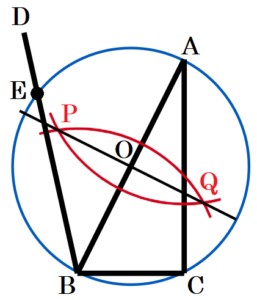
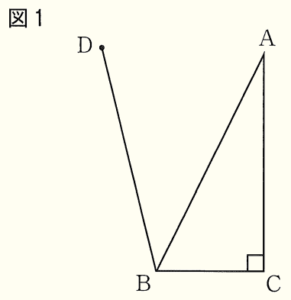
(1) 図1において,\( △ABC \) は \( ∠C=90° \) の直角三角形であり,点 \( D \) は \( △ABC \) の外部の点である。線分 \( BD \) 上にあり,\( ∠EBA=∠ECA \) となる点 \( E \) を定規とコンパスを使って図1に作図しなさい。ただし,作図に用いた線は消さないこと。
【解答】
手順1 点 \( A,B \) を中心に円弧を描く
(交点を \( P,Q \) とします)
手順2 点 \( P,Q \) を通る直線を描く
(辺 \( AB \) との交点を \( O \) とします)
手順3 点 \( O \) を中心に線分 \( OA \) を半径とする円を描く
手順3の円と線分 \( BD \) の交点が求める点 \( E \) になります。
【解説】
\( ∠EBA=∠ECA \) に注目すると,
2点 \( E,A \) が共通であることから,
4点 \( E,B,C,A \) が同一円周上にあるとき,
\( ∠EBA,∠ECA \) はどちらも \( \stackrel{\huge\frown}{ EA } \) に対する円周角になります。
このとき, \( \stackrel{\huge\frown}{ AB } \) に対する円周角 \( ∠ACB=90° \) であることから,
辺 \( AB \) がこの円の直径になります。
よって,辺 \( AB \) の中点がこの円の中心になり,
この円と線分 \( BD \) の交点が求める点 \( E \) になります。
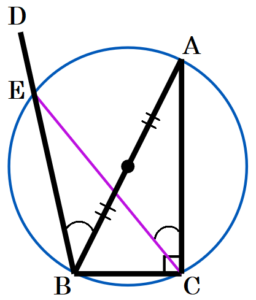
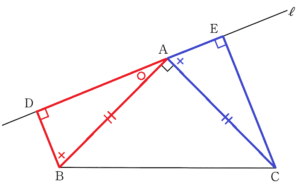
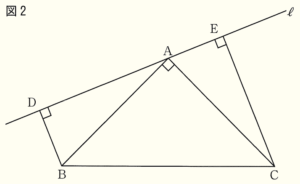
(2) 図2において,\( △ABC \) は \( AB=AC \) の直角二等辺三角形であり,点 \( A \) を通り,辺 \( BC \) に平行でない直線を ℓ とする。また,点 \( B,C \) から直線 ℓ にひいた垂線をそれぞれ \( BD,CE \) とする。このとき,\( △ABD≡△CAE \) であることを証明しなさい。
【解答】
\( △ABD \) と \( △CAE \) において,
仮定より \( AB=CA \) ・・・ ➀
\( BD,CE \) は、直線 ℓ に対する垂線なので,
\( ∠ADB=∠CEA=90° \) ・・・ ➁
三角形の内角の和は \( 180° \) なので,
\( ∠ABD=180°-(∠ADB+∠BAD) \)
\( =90°-∠BAD \) ・・・ ➂
3点 \( D,A,E \) は,直線 ℓ 上の点なので,
\( ∠CAE=180°-(∠BAD+∠BAC) \)
\( =90°-∠BAD \) ・・・ ➃
➂➃より,
\( ∠ABD=∠CAE \) ・・・ ➄
➀➁➄より,
斜辺と他の1鋭角が等しい直角三角形なので,
\( △ABD≡△CAE \)
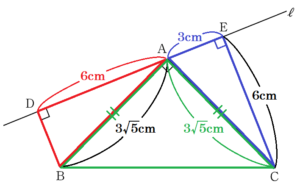
(3) (2)の図2において,\( AB=3√5 \; cm,CE=6 \; cm \) のとき,\( DE \) の長さを求めなさい。
【解説】
\( △ABC \) は \( AB=AC \) の直角二等辺三角形なので,
\( AC=AB=3√5 \; cm \)
\( △ACE \) において,三平方の定理より,
\( AE^2=(3√5)^2-6^2=9 \)
\( AE=3 \; (cm) \)
(2)より,\( △ABD≡△CAE \) なので,
\( AD=CE=6 \; cm \)
よって,\( DE=AD+AE=9 \; (cm) \)
大問7
関数 \( y=x^2 \) と点 \( A(1,1) \) について,次の(1),(2)に答えなさい。
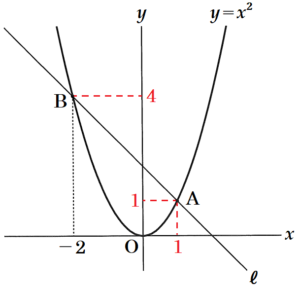
(1) 図1において,関数 \( y=x^2 \) のグラフと直線 ℓ との交点が点 \( A \) と点 \( B \) である。点 \( B \) の \( x \) 座標が \( -2 \) であるとき,直線 ℓ の式を求めなさい。
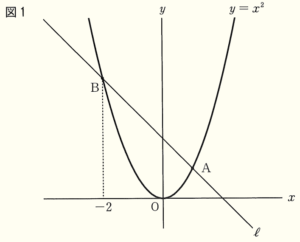
【解説】
点 \( B \) は,\( y=x^2 \) 上の点で,
\( x \) 座標が \( -2 \) なので,
\( y=(-2)^2=4 \)
直線 ℓ は,\( A(1,1),B(-2,4) \) を通るので,
直線 ℓ の式を \( y=ax+b \) とすると,
\( a=\dfrac{1-4}{1-(-2)}=-1 \)
\( y=-x+b \) に \( x=1,y=1 \) を代入すると,
\( 1=-1+b \)
\( b=2 \)
よって,直線 ℓ の式は \( y=-x+2 \) になります。
(2) 図2において,関数 \( y=x^2 \) のグラフと直線 \( m \) は2点 \( A,C \) で交わっている。直線 \( m \) の式は \( y=\dfrac{1}{2}x+\dfrac{1}{2} \) で,点 \( C \) の \( x \) 座標は \( -\dfrac{1}{2} \) である。直線 \( m \) と \( x \) 軸の交点を \( E \) とおき,線分 \( AC \) 上に点 \( P \) をとる。点 \( P,A \) から \( x \) 軸にひいた垂線をそれぞれ \( PM,AN \) とし,点 \( P \) の \( x \) 座標を \( t \) とする。
\( △EAN \) の面積が \( △EPM \) の面積の2倍となるとき,\( t \) の値を求めなさい。
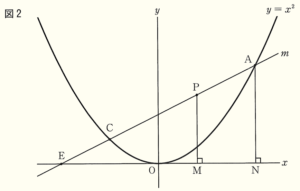
【解説】
\( △EAN \) と \( △EPM \) は,\( ∠E \) が共通,\( ∠ANE=∠PME=90° \) より,
\( △EAN \) ∽ \( △EPM \) になっています。
相似な図形の面積比は相似比の2乗の比と等しいので,
\( △EAN:△EPM-2:1 \) のとき,相似比は \( \sqrt{2}:1 \) になります。
つまり,\( AN:PM=\sqrt{2}:1 \) となるような \( t \) の値を求めればいいことになります。
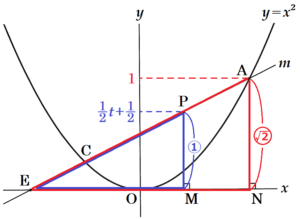
線分 \( AN \) は \( x \) 軸と垂直で,点 \( A \) の座標が \( A(1,1) \) であることから,
\( AN=1 \)
点 \( P \) は,\( y=\dfrac{1}{2}x+\dfrac{1}{2} \) 上の点で,\( x \) 座標が \( t \) なので,
\( y=\dfrac{1}{2}t+\dfrac{1}{2} \)
であり,線分 \( PM \) は \( x \) 軸と垂直であることから,
\( PM=\dfrac{1}{2}t+\dfrac{1}{2} \)
よって,\( AN:PM=\sqrt{2}:1 \) となるような \( t \) の値は,
\( 1:\left( \dfrac{1}{2}t+\dfrac{1}{2} \right)=\sqrt{2}:1 \)
\( 2:(t+1)=\sqrt{2}:1 \)
\( \sqrt{2}(t+1)=2 \)
\( t+1=\sqrt{2} \)
\( t=-1+\sqrt{2} \)
大問8
図形の計量について, 次の(1),(2)に答えなさい。ただし, 円周率は \( \pi{} \) とする。
(1) 図1のようなグラスの上の部分は,図2のように円すい型の容器とみなすことができる。ここに,\( 15 \; mL \) の水を入れたところ,この容器の高さのちょうど半分のところまで水が入った。このグラスの容積を求めなさい。
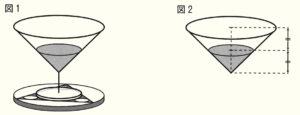
【解説】
容器の円すい形と入れた水の円すい形は相似であり,
水が容器の半分の高さまで入っていることから,
相似比は \( 2:1 \) になっています。
相似な立体の体積比は相似比の3乗の比と等しいので,
容器の体積と水の体積の比は \( 8:1 \) になります。
容器の体積を \( V \; mL \) とすると,
\( V:15=8:1 \)
\( V=120 \; (mL) \)
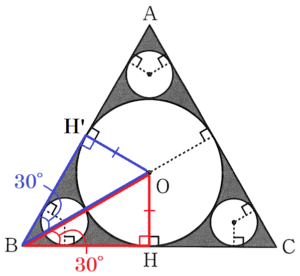
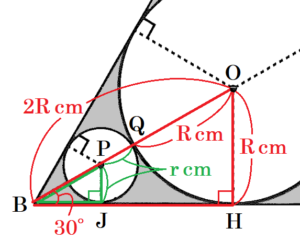
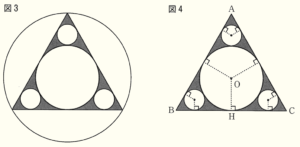
(2) グラスが置いてあるコースターに図3のような模様がかかれていた。図3の模様をもとに図4の図形を考える。円 \( O \) は正三角形 \( ABC \) の3辺に接しており,\( △ABC \) の内部には円 \( O \) 以外の3つの円があり,これらの3つの円はすべて円 \( O \) と \( △ABC \) の2辺に接している。円 \( O \) と辺 \( BC \) の接点を \( H \) とし,\( △ABC \) の内部にある大小4つの円の面積の和が \( 8\pi{} \; cm^2 \) に等しいとき,\( OH \) の長さを求めなさい。
【解答】
\( OH=\sqrt{6} \; cm \)
【解説】
この問題では長さの情報が与えられていないので,\( OH \) の長さ(\( R \) の値)は直接求められません。
そこで,大小4つの円の面積の和が \( 8\pi{} \; cm^2 \) であることから,
大きい円の半径を \( R \; cm \),小さい円の半径を \( r \; cm \) とすると,
\( \pi{} \times R^2+3\pi{} \times r^2=8\pi{} \)
と表すことができ,\( r \) を消すことができれば,この方程式を解いて \( R \) の値を求めることができます。
このタイプの問題の場合には,\( R \) を \( r \) を使った式で表す,または,\( r \) を \( R \) を使った式で表すことで
どちらか一方の文字を消すことができます。
円 \( O \) と辺 \( AB \) の接点を \( H’ \) とすると,
円 \( O \) の半径なので,\( OH=OH’ \) ・・・ ➀
円の半径と接線の関係より,\( ∠OHB=∠OH’B=90° \) ・・・ ➁
辺 \( OB \) は共通 ・・・ ➂
➀➁➂より,
直角三角形において,斜辺と他の1辺が等しいので,
\( △OHB≡△OH’B \)
\( △ABC \) は正三角形なので,\( ∠ABC=60° \) であり,
\( ∠OBH=\dfrac{1}{2}∠ABC=30° \)
これは,小さい円についても同じことが成り立っています。
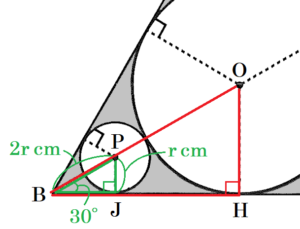
ここで,小さい円のうち,
辺 \( AB,AC \) に接する円の中心を \( P \) ,
円 \( P \) と辺 \( BC \) の接点を \( J \) とし,
\( PJ=r \; cm \) とすると,
\( △PBJ \) は \( 30°,60°,90° \) の直角三角形
なので,
\( PB=2PJ=2r \; (cm) \) ・・・ 【ア】
と表すことができます。
次に,\( OH=R \; cm \) とすると,
\( △OBH \) は \( 30°,60°,90° \) の直角三角形
なので,
\( OB=2OH=2R \; (cm) \)
また,円 \( O \) と円 \( P \) の交点を \( Q \) とすると,
\( OQ \) は円 \( O \) の半径なので,
\( OQ=OH=R \; cm \)
\( PQ \) は円 \( P \) の半径なので,
\( PQ=PJ=r \; cm \)
であり,
\( PB=OB-OQ-PQ \)
\( =2R-R-r \)
\( =R-r \; (cm) \) ・・・ 【イ】
と表すことができます。
【ア】【イ】より,
\( R-r=2r \)
\( r=\dfrac{R}{3} \)
大小4つの円の面積の和は
\( \pi{} \times R^2+3\pi{} \times r^2=8\pi{} \)
と表すことができるので,
\( \pi{} \times R^2+3\pi{} \times r^2=8\pi{} \)
\( \pi{} \times R^2+3\pi{} \times \left( \dfrac{R}{3} \right)^2=8\pi{} \)
\( R^2+\dfrac{1}{3}R^2=8 \)
\( R^2=6 \)
\( R=\sqrt{6} \; (cm) \) (\( R>0 \) より)











 自治体A ・・・ 第三四分位数が約49歳なので,50歳以下の人口は,
自治体A ・・・ 第三四分位数が約49歳なので,50歳以下の人口は,