大問1
1 \( 7+(-11) \)
【解説】
\( =7-11 \)
\( =-4 \)
2 \( \dfrac{8}{3} \div (-6)-\dfrac{1}{9} \)
【解説】
\( =\dfrac{8}{3 \times (-6)}-\dfrac{1}{9} \)
\( =-\dfrac{4}{9}-\dfrac{1}{9} \)
\( =-\dfrac{5}{9} \)
3 \( (-9)^2-5^2 \)
【解説】
\( =81-25 \)
\( =56 \)
4 \( 3\sqrt{5}+\sqrt{10} \div \sqrt{2} \)
【解説】
\( =3\sqrt{5}+\sqrt{5} \)
\( =4\sqrt{5} \)
5 \( -3x^2y \times 4y^2 \div (−6xy^2) \)
【解説】
\( =\dfrac{-3x^2y \times 4y^2}{−6xy^2} \)
\( =2xy \)
6 \( \dfrac{x+y}{4}-\dfrac{x-y}{8} \)
【解答】
\( \dfrac{x+3y}{8} \)
【解説】
\( =\dfrac{2(x+y)}{8}-\dfrac{x-y}{8} \)
\( =\dfrac{2(x+y)-(x-y)}{8} \)
\( =\dfrac{x+3y}{8} \)
大問2
1 2次方程式 \( x^2+4x-2=0 \) を解きなさい。
【解説】
この2次方程式を \( ax^2+bx+c=0 \) と考えると,\( a=1,+b=4,c=-2 \) なので,
\( x=\dfrac{-4±\sqrt{4^2-4 \times 1 \times (-2)}}{2 \times 1} \)
\( =\dfrac{-4±\sqrt{24}}{2} \)
\( =-2±\sqrt{6} \)
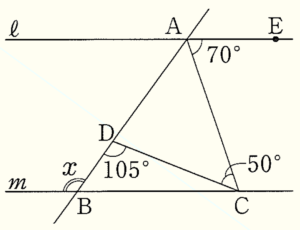
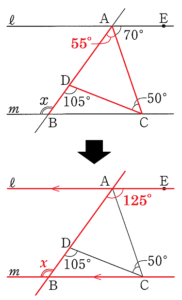
2 右の図において,2つの直線 \( ℓ,m \) は平行である。点 \( A,E \) は直線 \( ℓ \) 上の点,点 \( B,C \) は直線 \( m \) 上の点,点 \( D \) は直線 \( AB \) 上の点である。また,\( ∠EAC=70°,∠DCA=50°,∠CDB=105° \) である。
このとき,\( ∠x \) の大きさを求めなさい。
【解説】
\( ∠CDB=105° \) は \( △ACD \) の外角なので,
\( ∠CAD+50°=105° \)
\( ∠CAD=55° \)
ここから,
\( ∠BAE=55°+70°=125° \)
\( ℓ//m \) より,錯角は等しいので,
\( ∠x=∠BAE=125° \)
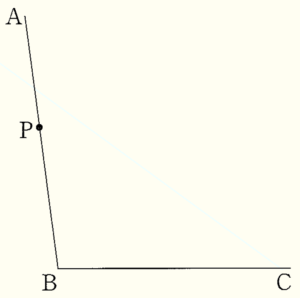
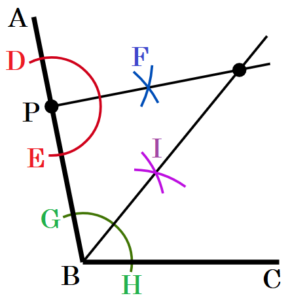
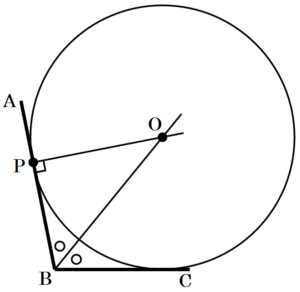
3 右の図において,半直線 \( BA,BC \) をともに接線とし,半直線 \( BA \) との接点を点 \( P \) とするような円の中心を作図によって求めなさい。そのとき,求めた点を ● で示しなさい。
ただし,作図には定規とコンパスを用い,作図に用いた線は消さずに残しておくこと。
【解答】
手順1 点 \( P \) を中心に円弧を描く。
(半直線 \( AB \) との交点を点 \( D,E \) とします)
手順2 点 \( D,E \) を中心に円弧を描く。
(交点を点 \( F \) とします)
手順3 点 \( P,F \) を通る直線を描く。
手順4 点 \( B \) を中心に円弧を描く。
(半直線 \( AB,AC \) との交点を点 \( G,H \) とします)
手順5 点 \( G,H \) を中心に円弧を描く。
(交点を点 \( I \) とします)
手順6 点 \( B,I \) を通る直線を描く。
手順3と手順6の直線の交点が求める点になります。
【解説】
円と接線については,以下の性質があるので,
これを利用して求める円の中心の位置を求めます。
(円の中心を \( O \) とします。)
・ 円の半径と接線は接点において垂直に交わる
・ 円 \( O \) の外部の点 \( B \) から2本の接線をひいたとき,直線 \( OB \) は \( ∠B \) の二等分線になる。(注)
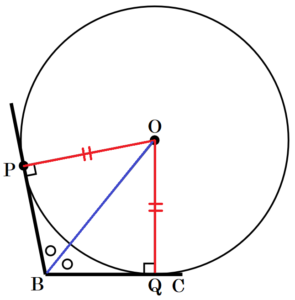
直線OBが∠Bの二等分線になる理由
接線 \( BC \) と円 \( O \) の接点を点 \( Q \) とすると,
\( △OBP \) と \( △OBQ \) において,
線分 \( OB \) は共通 ・・・ ➀
円 \( O \) の半径なので,\( OP=OQ \) ・・・ ➁
円の半径と接線は接点において垂直に交わるので,
\( ∠OPB=∠OQB=90° \) ・・・ ③
➀➁③より,
直角三角形において,斜辺と他の1辺がそれぞれ等しいので,
\( △OBP≡△OBQ \)
対応する角は等しいので,
\( ∠OBP=∠OBQ \)
4 \( y \) は \( x \) に反比例し,\( x=-1 \) のとき \( y=-4 \) である。このとき,この関係を表すグラフ上にある \( x \) 座標と \( y \) 座標がともに整数となる点の個数を求めなさい。
【解説】
反比例の式は,
\( y=\dfrac{a}{x} \) ( \( a \) は定数)
と表すことができるので,
\( x=-1,y=-4 \) を代入すると,
\( -4=\dfrac{a}{-1} \)
\( a=4 \)
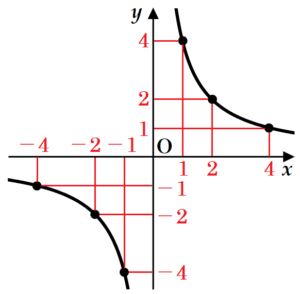
\( y=\dfrac{4}{x} \) において,
\( x \) 座標と \( y \) 座標がともに整数となるのは,
\( x \) と \( y \) の値がともに \( 4 \) の約数になるときです。
\( 4 \) の(正の)約数は \( 1,2,4 \) の3つなので,
グラフの曲線1本あたり3個になります。
反比例の曲線は原点 \( O \) について点対称な位置にもあるので,全部で6個になります。
5 箱の中に,赤球2個,青球1個,白球2個が入っている。この箱の中から球を同時に2個取り出したとき,取り出した球の中に青球が含まれる確率を求めなさい。
ただし,どの球を取り出すことも同様に確からしいものとする。
【解説】
赤球2個に「赤A」,「赤B」,白球2個に「白A」,「白B」と名前をつけると,
同時に2個取り出すので,「赤A・白A」と「白A・赤A」の組み合わせはまとめて1通りと考えられます。
これに注意して2個の球の組み合わせを樹形図として書き出すと,
青球が含まれる組み合わせは4通り,すべての組み合わせは10通りなので,
求める確率は,\( \dfrac{4}{10}=\dfrac{2}{5} \)

大問3
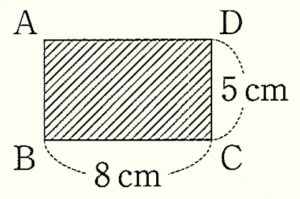
1 縦の長さが \( 5 \; cm \) ,横の長さが \( 8 \; cm \) の長方形の厚紙が4枚ある。これらの一部を切り取って異なる多角形の厚紙を作り,厚紙より大きい長方形の封筒の中に1枚ずつ入れた。
もとの厚紙を右のような長方形 \( ABCD \) とし,図1は,それぞれの多角形の厚紙を,封筒の右端から矢印の方向へ \( x \; cm \) 引き出した様子を模式的に表している。点 \( B,C \) は直線 \( ℓ \) 上にあり,封筒から出ている部分の面積を \( y \; cm^2 \) とすると,\( y \) は \( x \) の関数である。4つの多角形の,\( x \) と \( y \) の関係をそれぞれグラフに表したところ,図2のような折れ線となるものがあった。
このとき,次の(1),(2)に答えなさい。
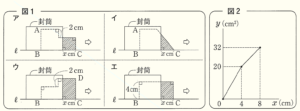
(1) 図2が表している \( x \) と \( y \) の関係は,どの多角形を引き出した場合であるか。その様子を表したものを,図1のア~エから1つ選び,その記号を書きなさい。
【解説】
\( 0≦x≦4 \) の範囲の直線に注目すると,\( y \) の値は同じ割合で増えているので,
イの三角形は正しくないとわかります。
グラフから,
\( 4 \; cm \) 引き出したとき,封筒から出ている部分の面積は \( 20 \; cm^2 \) なので,
\( 1 \; cm \) 引き出すごとに,封筒から出ている部分の面積は \( 5 \; cm^2 \) ずつ増えています 。
つまり,高さが \( 5 \; cm \) であればいいので,
あてはまるのは,ウになります。
(2) 図2のグラフについて,\( x \) の変域が \( 4≦x≦8 \) のとき,\( y \) を \( x \) の式で表しなさい。
【解説】
この部分の直線の式を \( y=ax+b \) とすると,
\( (4,20),(8,32) \) を通るので,
傾き \( a=\dfrac{32-20}{8-4}=3 \)
\( y=3x+b \) に \( x=4,y=20 \) を代入すると,
\( 20=3 \times 4+b \)
\( b=8 \)
以上より,求める式は \( y=3x+8 \)
2 「塩こうじ」という発酵調味料がある。野菜の分量に対して \( 12 \; \% \) の分量の「塩こうじ」で漬けて 「野菜の塩こうじ漬け」を作る。
Aさんは,にんじんと白菜の分量の比が \( 1:7 \) で書かれていたレシピをもとに,野菜の分量を \( n \; g \) としたときの材料の分量を表のようにまとめた。
このとき,次の(1)~(3)に答えなさい。
(1) 表の に当てはまる数量を,\( n \) を使った式で表しなさい。
【解説】
にんじんと白菜の分量の比が \( 1:7 \) なので,
にんじんの分量は白菜の分量の \( \dfrac{1}{7} \) になります。
よって,にんじんの分量は, \( \dfrac{7}{8}n \times \dfrac{1}{7}=\dfrac{1}{8}n \)
(2) 「塩こうじ」が \( 27 \; g \) ある。これを使って「野菜の塩こうじ漬け」を表のとおり作る。\( 240 \; g \) の野菜をすべて漬けようとするとき,「塩こうじ」はこの分量で足りるか。次のア,イから正しいものを1つ選び,その記号を書きなさい。また,それが正しいことの理由を表の式をもとに根拠を示して説明しなさい。
ア 「塩こうじ」は \( 27 \; g \) で足りる。
イ 「塩こうじ」は \( 27 \; g \) では足りない。
【解答】
イ
【理由】
表より,\( n \; g \) の野菜をすべて漬けるとき,必要な「塩こうじ」の分量は \( \dfrac{3}{25}n \) なので,
\( n=240 \) を代入すると,
\( \dfrac{3}{25} \times 240=\dfrac{144}{5}=28.8 \; (g) \)
となり,\( 27 \; g \) より多いから。
(3) Aさんが,「野菜の塩こうじ漬け」を作るために野菜を用意したところ,にんじんと白菜の分量の比が \( 1:10 \) であった。そこで,にんじんを \( 15 \; g \) 増やし,にんじんと白菜の分量の比が \( 1:7 \) になるよう調整した。このとき,必要な「塩こうじ」の分量を求めなさい。
【解説】
最初のにんじんの分量を \( x \; g \) とすると,白菜の分量は \( 10x \; g \) と表せます。
\( 15 \; g \) 増やした後のにんじんの分量は \( x+15 \; g \) と表すことができ,
にんじんと白菜の分量の比が \( 1:7 \) になったので,
\( (x+15):10x=1:7 \)
\( 7(x+15)=10x \)
\( x=35 \; (g) \)
ここから,
\( 15 \; g \) 増やした後のにんじんの分量は \( 35+15=50 \; (g) \),
\( 15 \; g \) 増やした後の野菜全体の分量は \( 50 \times 8=400 \; (g) \)
よって,\( 400 \; g \) の野菜をすべて漬けるのに必要な「塩こうじ」の分量は,
\( \dfrac{3}{25} \times 400=48 \; (g) \)
大問4
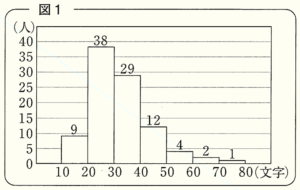
1 Bさんは,所属する学年の生徒95人で行われた,ある日の練習会における1分間あたりの文字入力数を記録し,図1のようなヒストグラムに表した。また,長方形の上に示されている数は,それぞれの階級の度数を表している。このとき,次の(1),(2)に答えなさい。
(1) 中央値が含まれる階級を求めなさい。
【解説】
学年全体の生徒数は95人なので,中央値になるのは,入力数の少ない方から48番目の値になります。
30文字未満の階級の度数は \( 9+39=47 \)(人) なので,
中央値が含まれる階級は,「30文字以上40文字未満」の階級になります。
(2) 1分間あたりの文字入力数が40文字以上の生徒の人数の割合は,全体の何%か求めなさい。
【解説】
1分間あたりの文字入力数が40文字以上の生徒の人数は,
\( 12+4+2+1=19 \)(人)
なので,割合は,
\( 19 \div 95 \times 100=20 \; (\%) \)
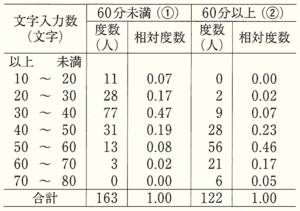
2 Bさんは,数か月後に行われた練習会で全校生徒285人を対象に1分間あたりの文字入力数を調べた。その際,1日あたりのICT機器を学習に用いた時間についても調べ,\( 60 \) 分未満( ① )の生徒と \( 60 \) 分以上( ② )の生徒に分け,それぞれについて相対度数を求め,右のような度数分布表に表した。
このとき,次の(1),(2)に答えなさい。
(1) 2つの分布の傾向を比べるために,相対度数を用いることについて,次のように理由を示した。 X に当てはまるものを下のア~エから1つ選び,その記号を書きなさい。
ア 学習時間の合計
イ 最大値
ウ 範囲
エ 全体の度数
【解説】
ある階級の度数が同じ10人であっても全体の度数が100人のときと1万人のときでは,
10人の重み(価値)が異なるので,度数で比較するのは不適切です。
(2) 図2は度数分布表をもとに,横軸を文字入力数,縦軸を相対度数として度数分布多角形(度数折れ線)に表したものである。図2から「1日あたりのICT機器を学習に用いた時間が \( 60 \) 分以上( ② )の生徒は,\( 60 \) 分未満( ① )の生徒より,1分間あたりの文字入力数が多い傾向にある」と主張することができる。そのように主張することができる根拠を,2つの度数分布多角形の特徴を比較して説明しなさい。
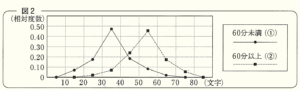
【解答(例)】
度数分布多角形において,\( 60 \) 分以上( ② )の山の部分の方が
\( 60 \) 分未満( ① )よりも右側にあるから。
大問5
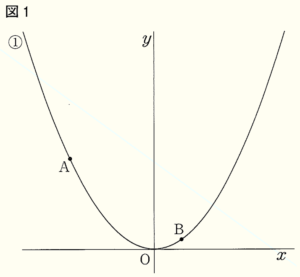
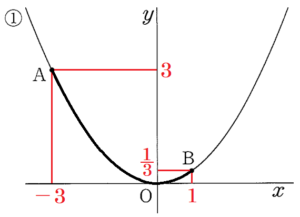
図1,2において,① は関数 \( y=\dfrac{1}{3}x^2 \) のグラフであり,点 \( A,B \) は ① 上にある。また,点 \( A \) の座標は \( (-3,3) \),点 \( B \) の \( y \) 座標は \( \dfrac{1}{3} \) である。ただし,点 \( B \) の \( x \) 座標は正とする。
このとき,次の1~3に答えなさい。
1 点 \( B \) の \( x \) 座標を求めなさい。
【解説】
\( y=\dfrac{1}{3}x^2 \) に \( y=\dfrac{1}{3} \) を代入すると,
\( \dfrac{1}{3}=\dfrac{1}{3}x^2 \)
\( x^2=1 \)
\( x=1 \) (\( x>0 \) より)
2 ① の関数 \( y=\dfrac{1}{3}x^2 \) において,\( x \) の変域が \( -3≦x≦1 \) のとき,\( y \) の変域を求めなさい。
【解説】
①は \( A(-3,3),B\left(1,\dfrac{1}{3} \right) \) を通っているので,
右のグラフより,\( 0≦y≦3 \)
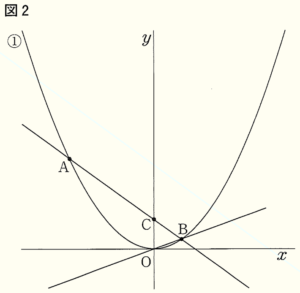
3 図2において,直線 \( AB \) と \( y \) 軸との交点を点 \( C \) とする。
このとき,次の(1),(2)に答えなさい。
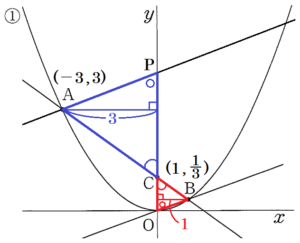
(1) 点 \( A \) を通り直線 \( OB \) に平行な直線と,\( y \) 軸との交点を点 \( P \) とするとき,\( △COB \) と \( △CPA \) の面積比を最も簡単な整数の比で表しなさい。
【解説】
\( △COB \) と \( △CPA \) において,
対頂角は等しいので,\( ∠BCO=∠ACP \) ・・・ ➀
\( OB//AP \) より,
錯角は等しいので,\( ∠BOC=∠APC \) ・・・ ➁
2組の角がそれぞれ等しいので,
\( △COB \) ∽ \( △CPA \)
\( △COB \) の底辺を線分 \( CO \) とすると,
高さは \( 1 \),
\( △CPA \) の底辺を線分 \( CP \) とすると,
高さは \( 3 \)
なので,相似比は \( 1:3 \)
相似な三角形の面積比は,相似比の2乗の比になるので,
\( △COB:△CPA=1^2:3^2=1:9 \)
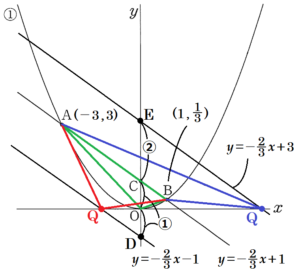
(2) \( x \) 軸上にある点 \( Q \) の \( x \) 座標を \( t \) とするとき,\( △AQB \) の面積が \( △AOB \) の面積の2倍となるような \( t \) の値をすべて求めなさい。
【解答】
\( t=-\dfrac{3}{2},\dfrac{9}{2} \)
【解説】
\( y \) 軸上に \( CD=2OC,CE=2OC \) となるように点 \( D,E \) をとるとき,
(点 \( D \) は直線 \( AB \) より下側,点 \( E \) は直線 \( AB \) より上側の点とします。)
\( △AQB \) と \( △AOB \) は,辺 \( AB \) が共通であることから,
点 \( D \) を通り,直線 \( AB \) と平行な直線上,
または,
点 \( E \) を通り,直線 \( AB \) と平行な直線上に
点 \( Q \) があるとき,\( △AQB=2△AOB \) となります。
(詳細は別途)
直線 \( AB \) の式を \( y=ax+b \) とすると,
\( a=\dfrac{\dfrac{1}{3}-3}{1-(-3)}=-\dfrac{2}{3} \)
\( y=-\dfrac{2}{3}x+b \) に \( x=-3,y=3 \) を代入すると,
\( 3=-\dfrac{2}{3} \times (-3)+b \)
\( b=1 \)
となり,直線 \( AB \) の式は \( y=-\dfrac{2}{3}x+1 \)
ここから,\( OC=1 \) なので,
\( CD=2 \) となるのは,\( D(0,-1) \) のとき,
\( CE=2 \) となるのは,\( E(0,3) \) のときです。
点 \( D \) を通り,直線 \( AB \) と平行な直線の式は \( y=-\dfrac{2}{3}x-1 \) なので,
\( x=t,y=0 \) を代入すると,
\( 0=-\dfrac{2}{3}t-1 \)
\( t=-\dfrac{3}{2} \)
点 \( E \) を通り,直線 \( AB \) と平行な直線の式は \( y=-\dfrac{2}{3}x+3 \) なので,
\( x=t,y=0 \) を代入すると,
\( 0=-\dfrac{2}{3}t+3 \)
\( t=\dfrac{9}{2} \)
CD=2OC,CE=2OCのとき,△AQB=2△AOBとなる理由
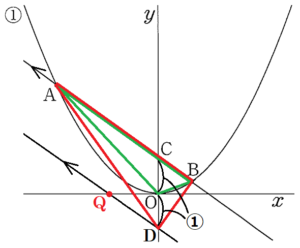
【点 \( D \) の場合】
\( y \) 軸上に \( CD=2OC \) となる点 \( D \) をとると,
\( △AOB=△AOC+△BOC \) ・・・ ➀
\( △ADB=△ADC+△BDC \) ・・・ ➁
\( △AOC \)と\( △ADC \),\( △BOC \)と\( △BDC \) は,
それぞれ高さが共通なので,
\( △AOC:△ADC=OC:CD=1:2 \)
\( △ADC=2△AOC \)
\( △BOC:△BDC=OC:CD=1:2 \)
\( △BDC=2△BOC \)
➁に代入すると,
\( △ADB=2△AOC+2△BOC \)
\( =2(△AOC+△BOC) \) ・・・ ③
➀➂より,
\( △ADB=2△AOB \)
点 \( D \) を通り,直線 \( AB \) と平行な直線と \( x \) 軸の交点を点 \( Q \) とすると,
等積変形になるので,
\( △AQB=△ADB=2△AOB \)
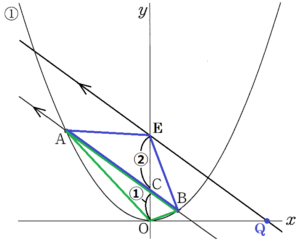
【点 \( E \) の場合】
\( y \) 軸上に \( CE=2OC \) となる点 \( E \) をとると,
\( △AOB=△AOC+△BOC \) ・・・ ➃
\( △AEB=△AEC+△BEC \) ・・・ ➄
\( △AOC \)と\( △AEC \),\( △BOC \)と\( △BEC \) は,
それぞれ高さが共通なので,
\( △AOC:△AEC=OC:CE=1:2 \)
\( △AEC=2△AOC \)
\( △BOC:△BEC=OC:CE=1:2 \)
\( △BEC=2△BOC \)
➄に代入すると,
\( △AEB=2△AOC+2△BOC \)
\( =2(△AOC+△BOC) \) ・・・ ⑥
➃➅より,
\( △AEB=2△AOB \)
点 \( E \) を通り,直線 \( AB \) と平行な直線と \( x \) 軸の交点を点 \( Q \) とすると,
等積変形になるので,
\( △AQB=△AEB=2△AOB \)
大問6
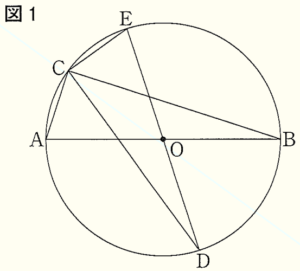
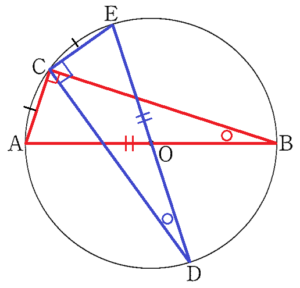
1 図1において,点 \( O \) は線分 \( AB \) を直径とする円の中心であり,
3点 \( C,D,E \) は円 \( O \) の周上にある点である。
5点 \( A, B,C,D,E \) は,図1のように \( A,D,B,E,C \) の順
で並んでいる。また,点 \( D,O,E \) は一直線上にあり,
弧 \( AC= \) 弧 \( CE \) である。
このとき,次の(1),(2)に答えなさい。
(1) \( △ABC≡△EDC \) となることを証明しなさい。
【解答】
\( △ABC \) と \( △EDC \) において,
円 \( O \) の直径なので,
\( AB=ED \) ・・・ ➀
直径に対する円周角なので,
\( ∠ACB=∠ECD=90° \) ・・・ ➁
\( ∠ABC \) は弧 \( AC \) の円周角,
\( ∠EDC \) は弧 \( CE \) の円周角なので,
弧 \( AC= \) 弧 \( CE \) より,
\( ∠ABC=∠EDC \) ・・・ ➂
➀➁➂より,
直角三角形の斜辺と他の1つの鋭角がそれぞれ等しいので,
\( △ABC≡△EDC \)
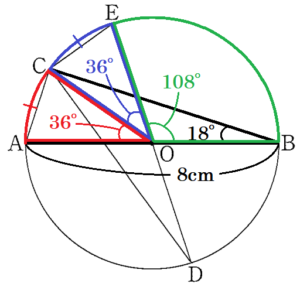
(2) \( AB=8 \; cm, ∠ABC=18° \) のとき,点 \( A \) を含まない弧 \( EB \) の長さを求めなさい。
【解答】
\( \dfrac{12}{5}\pi{} \; cm \)
【解説】
弧 \( AC \) の中心角なので,
\( ∠AOC=2∠ABC=36° \)
弧 \( AC= \) 弧 \( CE \) より,
\( ∠EOC=∠AOC=36° \)
ここから,
\( ∠BOE=180°-(∠AOC+∠EOC) \)
\( =108° \)
おうぎ形の弧の長さは,中心角に比例するので,
弧 \( EB=8\pi{} \times \dfrac{108°}{360°} \)
\( =8 \pi{} \times \dfrac{3}{10} \)
\( =\dfrac{12}{5}\pi{} \; (cm) \)
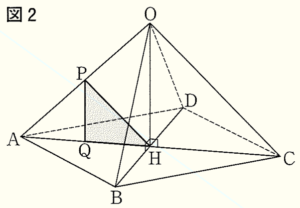
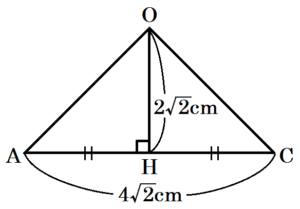
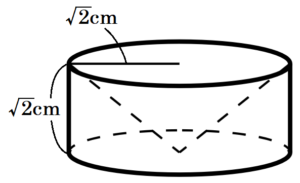
2 図2のような底面が正方形である正四角錐 \( OABCD \) がある。底面の対角線の交点を \( H \),辺 \( OA \) の中点を \( P \),線分 \( AH \) の中点を \( Q \) とする。また,底面の対角線の長さは \( 4\sqrt{2} \; cm \),線分 \( OH \) の長さは \( 2\sqrt{2} \; cm \) である。
このとき,次の(1)~(3)に答えなさい。
(1) 辺 \( OA \) の長さを求めなさい。
【解説】
線分 \( AC \) は底面の対角線なので,\( AC=4\sqrt{2} \; cm \)
正方形の対角線はそれぞれの中点で交わるので,
\( AH=\dfrac{1}{2}AC=2\sqrt{2} \; (cm) \)
\( OH⊥AC \) より,
\( △OAH \) は直角二等辺三角形なので,
\( OA=\sqrt{2}OH=4 \; (cm) \)
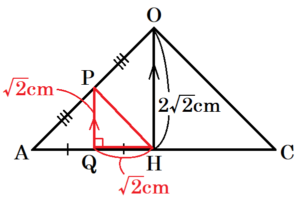
(2) \( △PQH \) を,直線 \( OH \) を軸として回転させてできる立体の体積を求めなさい。
【解答】
\( \dfrac{4\sqrt{2}}{3}\pi{} \; cm^3 \)
【解説】
\( △OAH \) において,
\( Q \) は線分 \( AH \) の中点なので,
\( QH=\dfrac{1}{2}AH=\sqrt{2} \; (cm) \)
また,中点連結定理より,
\( PQ//OH,PQ=\dfrac{1}{2}AH=\sqrt{2} \; (cm) \)
ここから,
\( △PQH \) を,直線 \( OH \) を軸として回転させてできる立体は,底面の半径と高さが \( \sqrt{2} \; cm \) の円柱 \( V_1 \) から底面の半径と高さが \( \sqrt{2} \; cm \) の円すい \( V_2 \) を取り除いた形になります。
\( V_1,V_2 \) の体積は,
\( V_1=(\pi{} \times \sqrt{2}^2) \times \sqrt{2}=2\sqrt{2}\pi{} \; (cm^3) \)
\( V_2=(\pi{} \times \sqrt{2}^2) \times \sqrt{2} \times \dfrac{1}{3}=\dfrac{2\sqrt{2}}{3}\pi{} \; (cm^3) \)
なので,
\( V_1-V_2=2\sqrt{2}\pi{}-\dfrac{2\sqrt{2}}{3}\pi{}=\dfrac{4\sqrt{2}}{3}\pi{} \; (cm^3) \)
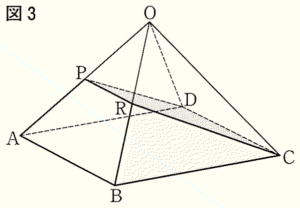
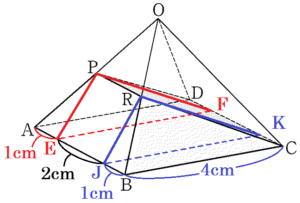
(3) 図3のように,図2の正四角錐において,辺 \( OB \) の中点を \( R \) とする。
このとき,6点 \( P,R,A,B,C,D \) を頂点とする立体の体積を求めなさい。
【解答】
\( \dfrac{20\sqrt{2}}{3} \; cm^3 \)
【解説】
\( P \) を通り面 \( ABCD \) と垂直な面と辺 \( AB ,CD\) との交点をそれぞれ \( E,F \),
\( R \) を通り面 \( ABCD \) と垂直な面と辺 \( AB ,CD\) との交点をそれぞれ \( J,K \) とすると,
求める立体は,
四角すい \( P-AEFD \),三角柱 \( PEF-RJK \),四角すい \( R-JBCK \)
の3つに分けることができます。
正方形 \( ABCD \) の対角線が \( 4\sqrt{2} \; cm \) なので,
1辺の長さは,\( 4\sqrt{2} \times \dfrac{1}{\sqrt{2}}=4 \; (cm) \)
\( △OAB \) において,中点連結定理より,
\( PR//AB,PR=\dfrac{1}{2}AB=2 \; (cm) \)
なので,
\( EJ=PR=2 \; cm,AE=BJ=1 \; cm \)
よって,
四角すい \( P-AEFD \) の体積は,
\( (AE \times AD) \times PQ \times \dfrac{1}{3}=(1 \times 4) \times \sqrt{2} \times \dfrac{1}{3}=\dfrac{4\sqrt{2}}{3} \; (cm^3) \)
三角柱 \( PEF-RJK \) の体積は,
\( \left( EF \times PQ \times \dfrac{1}{2} \right) \times EJ=\left( \sqrt{2} \times 4 \times \dfrac{1}{2} \right) \times 2=4\sqrt{2} \; (cm^3) \)
四角すい \( R-JBCK \) は,四角すい \( P-AEFD \) と合同なので,体積は,\( \dfrac{4\sqrt{2}}{3} \; (cm^3) \)
以上より,求める立体の体積は,
\( \dfrac{4\sqrt{2}}{3}+4\sqrt{2}+\dfrac{4\sqrt{2}}{3}=\dfrac{20\sqrt{2}}{3} \; (cm^3) \)