正の数と負の数
「算数」では、\( 0 \)(ゼロ)より大きい数について学んできましたが、
「数学」では,\( 0 \) より大きい数だけではなく,\( 0 \) より小さい数についても学んでいきます。
この単元で学ぶことは数学の基礎中の基礎で,これからいろいろ学んでいく中で当たり前のように使い続ける内容なので,確実にマスターしていきましょう。
(小数や分数も含みますが,\( 0 \) は含みません)
・ 小数点以下が \( 0 \) である数を整数といいます。
(小数や分数は含みませんが,\( 0 \) は含みます)
・ \( 0 \) より大きい整数を正の整数,\( 0 \) より小さい整数を負の整数といいます。
(小数や分数,\( 0 \) は含みません)
・ 正の整数のことを自然数といいます。
正の数と負の数
\( 0 \) より大きい数を 正の数(せいのすう),\( 0 \) より小さい数を 負の数(ふのすう)といい,
正の数,負の数には分数や小数も含みます。
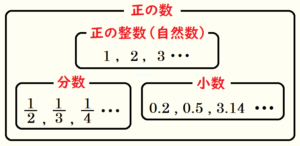
正の数とは
算数では,\( 0 \) より大きい整数,小数,分数について学習してきました。
それらをまとめて 正の数(せいのすう)といいます。
正の数は \( 0 \) よりどれだけ大きいかを表していて,数字の前に+(プラス)の記号をつけて、
\( +1 \;,+2 \;, ・・・ \) と書きます。
例:\( 0 \) より \( 1 \) 大きい数 → \( +1 \)
\( 0 \) より \( \dfrac{1}{2} \) 大きい数 → \( +\dfrac{1}{2} \)
正の数については、最初の+(プラス)を省略して,算数のときと同じように数字だけで表すことができます。
例: \( 1 \;,2 \;,3 \;,\dfrac{1}{2} \;,3.14 \;\; ・・・ \)
正の数(せいのすう)は「\( 0 \) より大きい」数なので,\( 0 \) は含みません。
\( A \) は \( 0 \) 「より」大きい → \( A>0 \) (\( 0 \) は含まない)
\( A \) は \( 0 \) 「より」小さい → \( A<0 \) (\( 0 \) は含まない)
\( A \) は \( 0 \) 「未満」 → \( A<0 \) (\( 0 \) は含まない)
\( A \) は \( 0 \) 「以上」 → \( A≧0 \) (\( 0 \) を含む)
\( A \) は \( 0 \) 「以下」 → \( A≦0 \) (\( 0 \) を含む)
負の数とは
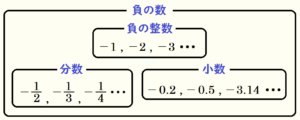
正の数に対して,\( 0 \) より小さい整数,小数,分数をまとめて 負の数(ふのすう)といいます。
負の数は \( 0 \) よりどれだけ小さいかを表していて,数字の前に-(マイナス)の記号をつけて、
\( -1 \;, -2 \; ・・・ \) と書きます。
例:\( 0 \) より \( 1 \) 小さい数 → \( -1 \)
\( 0 \) より \( \dfrac{1}{2} \) 小さい数 → \( -\dfrac{1}{2} \)
正の数の場合と違って、-(マイナス)は省略できませんので、必ず書いてください。
負の数(ふのすう)は「\( 0 \) より小さい」数なので,\( 0 \) は含みません。
整数と自然数
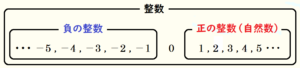
小数でも分数でもない,小数点以下が \( 0 \) になる切りのいい数を整数といい,
\( 0 \) より大きい整数を 正の整数 ,\( 0 \) より小さい整数を 負の整数 といいます。
\( 0 \) は 正の整数,負の整数 どちらにも含まれません。
つまり,整数は「正の整数」,「負の整数」,「\( 0 \)」の3種類に分けることができます。
また,正の整数は 自然数 と呼ばれることもあります。
【例題】
次の数の中から 正の数,負の数,整数,自然数,負の整数 のそれぞれにあてはまるものをすべて選びなさい。
\( \boxed{4 \;\;,\;\; -9 \;\;,\;\; \dfrac{3}{4} \;\;,\;\; 0 \;\;,\;\; 3.14 \;\;,\;\; -5 \;\;,\;\; -\dfrac{7}{3} \;\;,\;\; +8 \;\;,\;\; -2.1} \)
数学の世界での数直線
算数の世界では \( 0 \) より大きい数だけを扱っていたので,数直線は,一番小さい数 \( 0 \) を左端にしたものでした。
数学の世界では \( 0 \) より小さい数も扱うので,数直線も少し変わります。
数直線は右に行くほど大きい数,左に行くほど小さい数を表すので,
負の数は \( 0 \) より小さい数であることから,
負の数を表す数直線は,一番大きい数 \( 0 \) を右端にしたものになります。
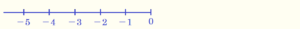
なので,数学の世界の数直線は,これら2つをくっつけたものになり,
\( 0 \) より右側が正の数,\( 0 \) より左側が負の数を表しています。
また,\( 0 \) を表す点を 原点 といいます。

負の数を数直線上に表す
負の数を数直線上に表す場合も考え方は正の数の場合と同じです。
例1:\( -2 \) を数直線上に表す
下の数直線で目盛1個は \( 1 \) を表していて,左に行くほど小さい数を表しています。
\( -2 \) は,\( 0 \) より \( 2 \) だけ小さい数を表しているので,
\( -2 \) を表す点は,\( 0 \) より目盛2個分だけ左の点になります。

例2:\( -\dfrac{3}{2} \) を数直線上に表す
下の数直線で大きい目盛1個は \( 1 \) を,小さい目盛1個は \( \dfrac{1}{2} \) を表していて,
左に行くほど小さい数を表しています。
\( -\dfrac{3}{2} \) は,\( 0 \) より \( \dfrac{3}{2} \) だけ小さい数を表していて,\( \dfrac{3}{2} \) は小さい目盛3個分になるので,
\( -\dfrac{3}{2} \) を表す点は,\( 0 \) より小さい目盛3個分だけ左の点になります。

数直線に数を表す方法(書き方)
1.その数が表すところに ●(黒丸)を書く
2.書き込んだ ●(黒丸)の上側にその数を 必ず 書く
(数直線の下側に書いてある数は目盛を表す数なので,書いていないものと考えます)

正の数・負の数を使っていろいろな量を表す
「-(マイナス)」の記号(符号)には,「反対」ということを表す効果があります。
例えば,乾電池のプラス極の反対側はマイナス極になっています。
正の数は基準となる値 \( 0 \) よりどれだけ大きいか,負の数は,基準となる値 \( 0 \) よりどれだけ小さいかを表していて,ある基準に対して反対の性質を表しています。
例:\( \color{red}{+}2 \) ・・・ \( 0 \) より \( 2 \) 大きい
\( \color{blue}{-}2 \) ・・・ \( 0 \) より \( 2 \) 小さい
これを利用して,「-(マイナス)」をつけることによっていろいろな量に対して反対の意味を表すことができます。
反対の性質を持つ量(増える減る・高い低いなど)を表す
身近な \( 0 \) より小さい量の例として「気温 \( -2 \; C^\circ \)」について考えてみます。
「気温 \( \color{red}{+}2 \; C^\circ \)」は,水が凍り始める温度「\( 0 \; C^\circ \)」より \( 2 \; C^\circ \) 髙い温度を表しています。
これに対して,
「気温 \( \color{blue}{-}2 \; C^\circ \)」は,水が凍り始める温度「\( 0 \; C^\circ \)」より \( 2 \; C^\circ \) 低い温度を表しています。
数直線で考えると,数直線は右に行くほど値は大きくなる,左に行くほど値は小さくなるので,
一般的には,「増える」,「髙い」,「重い」を正の数,「減る」,「低い」,「軽い」を負の数
を使って表すことが多いです。
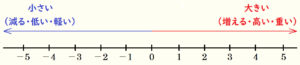
このように考えると,
体重が \( 5 \; kg \) 増えたことを \( \color{red}{+}5 \; kg \) と表すとき,
体重が \( 5 \; kg \) 減ったことは \( \color{blue}{-}5 \; kg \) と表すことができます。

このように,いろいろな値に「-(マイナス)」をつけることによって,反対の意味を持つ値を表すことができます。
・ \( 5 \; cm \) 高いことを \( \color{red}{+}5 \; cm \) と表すとき,\( 5 \; cm \) 低いことは \( \color{blue}{-}5 \; cm \) と表すことができます。
・ \( 5 \; cm \) 長いことを \( \color{red}{+}5 \; cm \) と表すとき,\( 5 \; cm \) 短いことは \( \color{blue}{-}5 \; cm \) と表すことができます。
・ \( 5 \) 分後を \( \color{red}{+}5 \) 分と表すとき,\( 5 \) 分前は \( \color{blue}{-}5 \) 分と表すことができます。
・ 北へ \( 500 \; m \) 進むことを \( \color{red}{+}500 \; m \) と表すとき,
南へ \( 500 \; m \) 進むことは \( \color{blue}{-}500 \; m \) と表すことができます。
基準となる値との差を表す
\( 0 \) ではないある値を基準として,基準となる値との差を正の数,負の数を使って表すことで,より簡単に表すことができます。
例えば,A~Fの6人が合格点が \( 60 \) 点に設定されているテストを受け,結果は下の表のとおりであったとします。
このとき,A~Fの得点と合格点 \( 60 \) 点との差を合格点より高い得点を正の数,低い得点を負の数として表してみます。
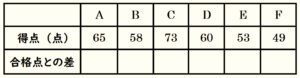
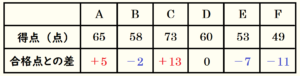
このとき,合格点 \( 60 \) 点を基準とすると,
Aの得点は \( 65 \) 点で,合格点 \( 60 \) 点より \( 5 \) 点高いので,差は \( +5 \) 点と表すことができます。
Bの得点は \( 58 \) 点で,合格点 \( 60 \) 点より \( 2 \) 点低いので,差は \( -2 \) 点と表すことができます。
Cの得点は \( 73 \) 点で,合格点 \( 60 \) 点より \( 13 \) 点高いので,差は \( +13 \) 点と表すことができます。
Dの得点は \( 60 \) 点で,合格点 \( 60 \) 点と等しいので,差は \( 0 \) 点と表すことができます。
Eの得点は \( 53 \) 点で,合格点 \( 60 \) 点より \( 7 \) 点低いので,差は \( -7 \) 点と表すことができます。
Fの得点は \( 49 \) 点で,合格点 \( 60 \) 点より \( 11 \) 点低いので,差は \( -11 \) 点と表すことができます。
同じ意味のことを反対の言葉を使って言い換える
また,この他にも,体重が \( 5 \; kg \) 増えたことを,意味を変えないように体重が \( \color{blue}{-}5 \; kg \) 減ったと言いかえることができます。
これは,「増えた」を「減った」という反対の意味の言葉に変えているので,値の方も反対を表す \( \color{blue}{-}5 \; kg \) に変えることで,意味が同じになるようにしています。

・ \( 5 \; cm \) 高い ⇔ \( \color{blue}{-}5 \; cm \) 低い
・ \( 5 \; cm \) 長い ⇔ \( \color{blue}{-}5 \; cm \) 短い
・ \( 5 \) 分後 ⇔ \( \color{blue}{-}5 \) 分前
・ 北へ \( 500 \; m \) 進む ⇔ 南へ \( \color{blue}{-}500 \; m \) 進む
絶対値と数の大小
符号を変える
\( +2 \) から \( -2 \),\( -5 \) から \( +5 \) などのように,数字はそのままで符号だけをとりかえることを 符号を変える といいます。
\( +2 \) と \( -2 \) はどちらも数直線上における \( 0 \) からの距離は \( 2 \) ,
\( -5 \) と \( +5 \) はどちらも数直線上における \( 0 \) からの距離は \( 5 \)
になっていて,符号を変えた2つの数は数直線上における \( 0 \) からの距離が等しくなります。

絶対値とは
絶対値とは、数直線上で原点からの距離を表す値のことです。
\( \color{red}{+}2 \) は,原点からの距離が \( 2 \) なので,絶対値は \( 2 \)
\( \color{blue}{-}5 \) は,原点からの距離が \( 5 \) なので,絶対値は \( 5 \)
となります。

また,\( \color{red}{+}2 \) と \( \color{blue}{-}2 \) は,どちらも原点からの距離が \( 2 \) なので,
絶対値は \( 2 \) になります。ここから,符号をはずした数が絶対値になると考えることができます。
例:\( \color{red}{+}2 \) から符号(+)をはずすと \( +2 \) → \( 2 \) なので,絶対値は \( 2 \)
\( \color{blue}{-}2 \) から符号(-)をはずすと \( -2 \) → \( 2 \) なので,絶対値は \( 2 \)

ここから,絶対値が等しくなる数は正の数,負の数各1個ずつ,つまり2個存在する( \( 0 \) は除く)ことになります。
ここから,絶対値についてテストでよく出るパターンについて考えます。
絶対値が ○ 以下の整数
例として「絶対値が \( 3 \) 以下の整数」について考えます。
絶対値は符号をはずした数なので,「絶対値が \( 3 \) 以下」(注)になるとき,
あてはまる絶対値は,\( 3,2,1,0 \) になります。
絶対値が \( 3 \) の整数は,\( 3 \) と \( -3 \)
絶対値が \( 2 \) の整数は,\( 2 \) と \( -2 \)
絶対値が \( 1 \) の整数は,\( 1 \) と \( -1 \)
絶対値が \( 0 \) の整数は,\( 0 \)
なので,「絶対値が \( 3 \) 以下の整数」は \( 3,2,1,0,-1,-2,-3 \) の7個になります。
\( 3 \) 「以下」の場合は \( 3 \) を含みます。
\( 3 \) 「未満」 または \( 3 \) 「より小さい」の場合は \( 3 \) を含みません。
絶対値が ○ より小さい整数
例として「絶対値が \( 3 \) より小さい整数」について考えます。
絶対値は符号をはずした数なので,「絶対値が \( 3 \) より小さく」なるとき,
あてはまる絶対値は,\( 2,1,0 \) になります。
絶対値が \( 2 \) となる整数は,\( 2 \) と \( -2 \)
絶対値が \( 1 \) となる整数は,\( 1 \) と \( -1 \)
絶対値が \( 0 \) となる整数は,\( 0 \)
なので,「絶対値が \( 3 \) より小さい整数」は \( 2,1,0,-1,-2 \) の5個になります。
ちなみに,「絶対値が \( 3 \) 未満の整数」の場合も考え方,結果は同じになります。
絶対値が ○ 以上 △ 未満の整数
例として「絶対値が \( 2 \) 以上 \( 5 \) 未満の整数」について考えます。
絶対値は符号をはずした数なので,「絶対値が \( 2 \) 以上 \( 5 \) 未満」(注)になるとき,
あてはまる絶対値は,\( 4,3,2 \) になります。
ここから,
絶対値が \( 4 \) の整数は,\( 4 \) と \( -4 \)
絶対値が \( 3 \) の整数は,\( 3 \) と \( -3 \)
絶対値が \( 2 \) の整数は,\( 2 \) と \( -2 \)
なので,「絶対値が \( 2 \) 以上 \( 5 \) 未満の整数」は \( 4,3,2,-2,-3,-4 \) の6個になります。
\( 3 \) 「以上」の場合は \( 3 \) を含みます。
\( 3 \) 「より大きい」の場合は \( 3 \) を含みません。
正の数・負の数の大小
正の数・負の数で表されたいろいろな数の大小を比較する方法を考えます。
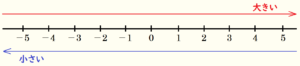
数直線上に書き出して考える
数直線では,右に行くほど大きい数,左に行くほど小さい数を表しているので,
比較する数が数直線上のどの位置にあるか調べることで大小を比較することができます。
正の数どうしの大小を比較する
正の数は \( 0 \) より大きい数なので,数字が大きい数ほど数直線の右側に位置しています。
ここから,正の数どうしの場合は,数字が大きい数ほど大きいことになります。
例:\( 2 \) と \( 5 \) の大小を比較する
\( 2 \) と \( 5 \) を数直線上に表すと,数字が大きい数 \( 5 \) の方が右側に位置しているので,
\( 5 \) は \( 2 \) より大きい(\( 2 \) は \( 5 \) より小さい)といえます。

負の数どうしの大小を比較する
負の数は \( 0 \) より小さい数なので,数字が大きい数ほど数直線の左側に位置しています。
ここから,負の数どうしの場合は,数字が大きい数ほど小さいことになります。
例:\( -2 \) と \( -5 \) の大小を比較する
\( -2 \) と \( -5 \) を数直線上に表すと,数字が大きい数 \( -5 \) の方が左側に位置しているので,
\( -5 \) は \( -2 \) より小さい(\( -2 \) は \( -5 \) より大きい)といえます。

正の数と負の数の大小を比較する
正の数は \( 0 \) より大きい数,負の数は \( 0 \) より小さい数なので,
数直線で表すと,正の数は \( 0 \) より右側,負の数は \( 0 \) より左側に位置しています。
ここから,正の数と負の数の場合は,必ず正の数の方が大きいことになります。
例として,\( 2 \) と \( -5 \) を数直線上に表すと,正の数 \( 2 \) の方が右側に位置しています。
例:\( 2 \) と \( -5 \) の大小を比較する
\( 2 \) と \( -5 \) を数直線上に表すと,正の数 \( 2 \) の方が右側に位置しているので,
\( 2 \) は \( -5 \) より大きい(\( -5 \) は \( 2 \) より小さい)といえます。

数直線を使わずに大小を比較する
以上のように,数直線上にそれぞれの数を書き出すことで,複数の数を比較することができますが,
毎回数直線を書いていたのでは,時間がかかってしまいます。
ここまでで数の大小を表す性質
・ 正の数どうしの場合は,数字が大きい数ほど大きい
・ 負の数どうしの場合は,数字が大きい数ほど小さい
・ 正の数と負の数の場合は,必ず正の数の方が大きい
がわかったので,慣れてきたら,以下の手順で数直線を書かずに頭の中で比較するようにしましょう。
2つの数を比較する場合
手順1.それぞれの数の符号を確認する。
符号が異なっていれば,正の数の方が大きい
手順2.符号が同じであれば,符号をはずした数字だけで大小を比較する。
正の数どうしの場合 ・・・ 符号をはずした数字が大きい方が大きい
負の数どうしの場合 ・・・ 符号をはずした数字が大きい方が小さい
3つ以上の数を比較する場合
手順1.それぞれの数の符号を確認し,負の数のグループ(と \( 0 \) )と正の数のグループに分ける
手順2.負の数だけで符号をはずして数字の大小を比較する。
手順3.数字の大きいほうから順に左から並べる。
手順4.正の数だけで符号をはずして数字の大小を比較する。
手順5.数字の小さいほうから順に左から並べる。
例として,次の大小を比較し,小さい順に並べてみます。
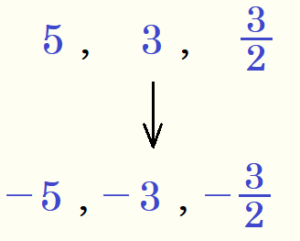
\( -\dfrac{3}{2},2,-5,0,-3,1.5 \)
手順1.それぞれの数の符号を確認し,負の数のグループ(と \( 0 \) )と正の数のグループに分ける
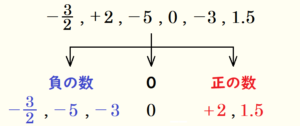
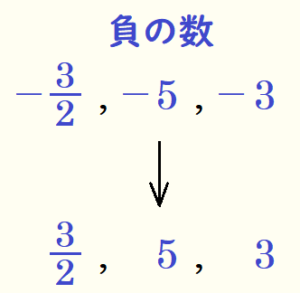
手順2.負の数だけ符号をはずす。
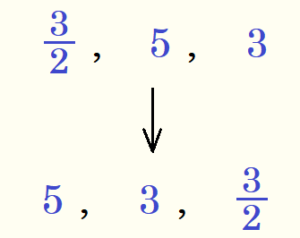
手順3.数字の大きいほうから順に左から並べる。
手順4.符号を戻す。
手順5.正の数だけで符号をはずす。
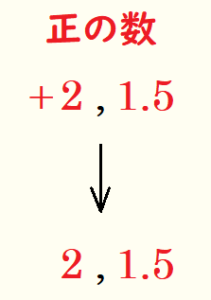
手順6.数字の小さいほうから順に左から並べる。
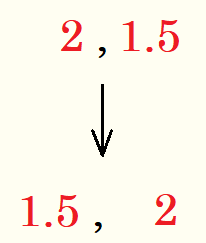
手順7.符号を戻す。
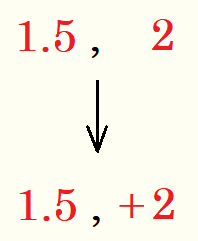
手順8.負の数のグループ(と \( 0 \) )と正の数のグループをすべてくっつけて左から順に書く。
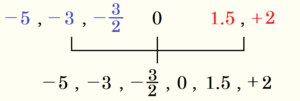
手順1~7をまとめると,こんな感じになります。

数の大小を記号を使って表す
数の大小は記号を使って簡単に表すことができます。
例えば,\( 2 \) と \( -5 \) の大小を記号を使って表すと
\( 2>-5 \) または \( -5<2 \)
となります。
この「>」や「<」の記号を 不等号 といい,大きい数の方が開く向きに書きます。
上の例の場合,\( 2 \) の方が大きいので,\( 2 \) が書いてある方が開くように書きます。
また,読み方は「>」が「大(だい)なり」,「<」が「小(しょう)なり」で,
\( 2>-5 \) と書いてある場合は「\( 2 \) 大なり \( -5 \)」
\( -5<2 \) と書いてある場合は「\( -5 \) 小なり \( 2 \)」
と読みます。
絶対値の大小と数の大小の関係
正の数どうしの絶対値の大小を比較すると・・・
絶対値の大小と数の大小の関係は必ず同じになります。
例:\( 2 \) と \( 5 \) の絶対値の大小と数の大小の関係を確認する
\( 2 \) の絶対値と \( 5 \) の絶対値の大小を比較すると,
\( 2 \) の絶対値は \( 2 \),\( 5 \) の絶対値は \( 5 \) なので,\( 5 \) の絶対値の方が大きくなります。
\( 2 \) と \( 5 \) の大小を比較すると,\( 5 \) の方が大きいので,
絶対値の大小と数の大小の関係はどちらも同じになります。
負の数どうしの絶対値の大小を比較すると・・・
絶対値の大小と数の大小の関係は必ず反対になります。
例:\( -2 \) と \( -5 \) の絶対値の大小と数の大小の関係を確認する
\( -2 \) の絶対値と \( -5 \) の絶対値の大小を比較すると,
\( -2 \) の絶対値は \( 2 \),\( -5 \) の絶対値は \( 5 \) なので,\( -5 \) の絶対値の方が大きくなります。
\( -2 \) と \( -5 \) の大小を比較すると,\( -2 \) の方が大きいので,
絶対値の大小と数の大小の関係は反対になります。
正の数と負の数の絶対値の大小を比較すると・・・
絶対値の大小と数の大小の関係は比較する数によって異なります。
例1:\( 2 \) と \( -5 \) の絶対値の大小と数の大小の関係を確認する
\( 2 \) の絶対値と \( -5 \) の絶対値の大小を比較すると,
\( 2 \) の絶対値は \( 2 \),\( -5 \) の絶対値は \( 5 \) なので,\( -5 \) の絶対値の方が大きくなります。
\( 2 \) と \( -5 \) の大小を比較すると,\( 2 \) の方が大きいので,
絶対値の大小と数の大小の関係は反対になります。
例2:\( 4 \) と \( -3 \) の絶対値の大小と数の大小の関係を確認する
\( 4 \) の絶対値と \( -3 \) の絶対値の大小を比較すると,
\( 4 \) の絶対値は \( 4 \),\( -3 \) の絶対値は \( 3 \) なので,\( 4 \) の絶対値の方が大きくなります。
\( 4 \) と \( -3 \) の大小を比較すると,\( 4 \) の方が大きいので,
絶対値の大小と数の大小の関係はどちらも同じになります。
数直線を使っていろいろな数を求める
ここまでは,正の数・負の数を \( 0 \) を基準としていろいろな数を表してきました。
たとえば,\( -5 \) は \( 0 \) より \( 5 \) 小さい数を表していますが,
逆に,\( 0 \) は \( -5 \) より \( 5 \) 大きい数と考えることもできます。

いくつかの例を使って,数直線を使っていろいろな数を求める方法を考えてみます。
例1.\( -3 \) より \( 4 \) 大きい数を求める
数直線では右に行くほど大きい値になるので,
「\( -3 \) より \( 4 \) 大きい数」は,数直線上で \( -3 \) から右に \( 4 \) 進んだところの数 \( 1 \) になります。

例2.\( 4 \) より \( 6 \) 小さい数を求める
数直線では左に行くほど小さい値になるので,
「\( 4 \) より \( 6 \) 小さい数」は,数直線上で \( 4 \) から左に \( 6 \) 進んだところの数 \( -2 \) になります。

例3.\( -1 \) より \( -3 \) 大きい数を求める
「\( -3 \) 大きい数」は「\( 3 \) 小さい数」と言い換えることができる(理由はコチラ)ので,
「\( -1 \) より \( -3 \) 大きい数」は「\( -1 \) より \( 3 \) 小さい数」と同じになります。
数直線では左に行くほど小さい値になるので,
「\( -1 \) より \( 3 \) 小さい数」は,数直線上で \( -1 \) から左に \( 3 \) 進んだところの数 \( -4 \) になります。

例4.\( -2 \) より \( -4 \) 小さい数を求める
「\( -4 \) 小さい数」は「\( 4 \) 大きい数」と言い換えることができる(理由はコチラ)ので,
「\( -2 \) より \( -4 \) 小さい数」は「\( -2 \) より \( 4 \) 大きい数」と同じになります。
数直線では右に行くほど大きい値になるので,
「\( -2 \) より \( 4 \) 大きい数」は,数直線上で \( -2 \) から右に \( 4 \) 進んだところの数 \( 2 \) になります。



