正の数・負の数のかけ算
ここでは,正の数・負の数のひき算について解説していきます。
かけ算のことを 乗法(じょうぽう) ,かけ算(乗法)によって求められた結果を 積 と呼びます。
2つの数が同じ符号の場合は,絶対値の積に「 + 」の符号をつける
2つの数が異なる符号の場合は,絶対値の積に「 - 」の符号をつける
3つ以上の数のかけ算の場合
式の中に含まれる負の数が奇数個の場合,絶対値の積に「 - 」の符号をつける
式の中に含まれる負の数が偶数個の場合は,絶対値の積に「 + 」の符号をつける
正の数 \( \times \) 正の数の場合
これは,算数で学んだなじみのあるかけ算になります。
例として \( 2 \times 3 \) について考えてみます。
「\( 2 \) に \( 3 \) をかけた数」ということは,「\( 2 \) を3個分たした数」を表すので,
数直線を使って考えると

つまり,\( 2 \times 3=6 \) となります。
負の数 \( \times \) 正の数の場合
例として \( -2 \times 3 \) について考えてみます。
「\( -2 \) に \( 3 \) をかけた数」ということは,「\( -2 \) を3個分たした数」を表すので,
数直線を使って考えると

つまり,\( -2 \times 3=-6 \) となります。
正の数 \( \times \) 負の数の場合
例として \( 2 \times (-3) \) について考えてみます。
「\( 2 \) に \( -3 \) をかけた数」ということは,「\( 2 \) を反対向きに3個分たした数」を表し,
「\( 2 \) を反対向きに3個分たした数」は「\( -2 \) を3個分たした数」と同じことなので,
数直線を使って考えると

つまり,\( 2 \times (-3)=-6 \) となります。
負の数 \( \times \) 負の数の場合
例として \( -2 \times (-3) \) について考えてみます。
「\( -2 \) に \( -3 \) をかけた数」ということは,「\( -2 \) を反対向きに3個分たした数」を表し,
「\( -2 \) を反対向きに3個分たした数」は「\( 2 \) を3個分たした数」と同じことなので,
数直線を使って考えると

つまり,\( -2 \times (-3)=6 \) となります。
乗法の交換法則と結合法則
乗法の交換法則
かけ算の式においては,かける順番を入れ替えても計算結果は等しくなります。
〇 \( \times \) □ \( = \) □ \( \times \) 〇
これを 乗法の交換法則 といいます。
例として,\( 2 \times (-3) \) と \( -3 \times 2 \) について考えてみます。
● \( 2 \times (-3) \) の場合
\( 2 \times (-3) \) は,「\( 2 \) を反対向きに3個分たした数」なので,

● \( -3 \times 2 \) の場合
\( -3 \times 2 \) は,「\( -3 \) を2個分たした数」なので,
となり,どちらの場合も計算結果は \( -6 \) で等しくなります。
乗法の結合法則
3個以上の数をかける場合にかける順番を入れ替えても計算結果は等しくなります。
\( ( \) 〇 \( \times \) △ \( ) \; \times \) □ \( = \) 〇 \( \times \; ( \) △ \( \times \) □ \( ) \)
これを 乗法の結合法則 といいます。
ここから,
〇 \( \times \) △ \( \times \) □ \( = \) 〇 \( \times \) □ \( \times \) △
\( = \) △ \( \times \) 〇 \( \times \) □ \( = \) △ \( \times \) □ \( \times \) 〇
\( = \) □ \( \times \) 〇 \( \times \) △ \( = \) □ \( \times \) △ \( \times \) 〇
例として,\( 2 \times 3 \times 4 \) の場合を考えてみます。
\( 2 \times 3 \) を先に計算する場合は,\( (2 \times 3) \times 4=6 \times 4=24 \)
\( 3 \times 4 \) を先に計算する場合は,\( 2 \times (3 \times 4)=2 \times 12=24 \)
となり,どちらの計算方法でも和は \( 24 \) で等しくなっています。
● 負の数を含む場合はどうなる?
乗法の結合法則は負の数を含んだかけ算でも成り立ちます。
例として,\( 2 \times (-3) \times 4 \) の場合を考えてみます。
\( 2 \times (-3) \) を先に計算する場合は,\( \{2 \times (-3)\} \times 4=-6 \times 4=-24 \)
\( (-3) \times 4 \) を先に計算する場合は,\( 2 \times \{(-3) \times 4\}=2 \times (-12)=-24 \)
となり,どちらの計算方法でも和は \( -24 \) で等しくなります。
● どんなときに使うの?
結合法則により計算順序をかえることで計算しやすくなります。
例として,\( 6 \times 2 \times 5 \) の場合を考えてみます。
前から順番に計算する場合は,\( 6 \times 2 \times 5=12 \times 5=60 \)
\( 2 \times 5 \) を先に計算すると,\( 6 \times 2 \times 5=6 \times 10=60 \)
となり,\( 2 \times 5 \) を先に計算することで,途中で \( 10 \) という切りのいい数が出てきて,
より簡単に計算できるようになります。
正の数・負の数のかけ算の結果をまとめると・・・
正の数・負の数のかけ算の結果は絶対値どうしの積に「 + 」または「 - 」の符号をくっつけることで求められます。
2つの数のかけ算
例えば,\( -2 \) を \( 2 \times (-1) \) つまり,\( 2 \) に\( -1 \) をかけてできた数と考えると,
\( -2 \) と \( 2 \) は,絶対値が同じで符号だけを入れ替えた関係にあることから,
\( -1 \) をかけるということは「 + 」→「 - 」または「 - 」→「 + 」に符号を入れ替えることと同じであると考えることができます。
これをもとに負の数を含むかけ算の積について考えると,次のようになります。
● 負の数 \( \times \) 正の数 の場合 (例:\( -2 \times 3 \) )

● 正の数 \( \times \) 負の数 の場合 (例:\( 2 \times (-3) \) )

● 負の数 \( \times \) 負の数 の場合 (例:\( -2 \times (-3) \) )
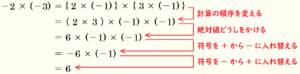
となります。
以上のことから,正の数・負の数のかけ算の結果をまとめると次のようになります。

つまり,
2つの数が同じ符号の場合は,絶対値の積に「 + 」の符号をつける
2つの数が異なる符号の場合は,絶対値の積に「 - 」の符号をつける
ことになります。
3つ以上の数のかけ算
先程の2つの数のかけ算のときと同じ考え方で負の数が3個の場合と4個の場合について符号がどのようになるか確認します。
● 負の項が3個の場合 (例:\( -2 \times (-3) \times (-4) \) )
\( -2 \times (-3) \times (-4)=\{ 2 \times (-1) \} \times \{ 3 \times (-1) \} \times \{ 4 \times (-1) \} \)
\( =(2 \times 3 \times 4) \times (-1) \times (-1) \times (-1) \)
\( =24 \times (-1) \times (-1) \times (-1) \)
\( =-24 \times (-1) \times (-1) \)
\( =24 \times (-1) \)
\( =-24 \)
● 負の項が4個の場合 (例:\( -2 \times (-3) \times (-4) \times (-5) \) )
\( -2 \times (-3) \times (-4) \times (-5)=\{ 2 \times (-1) \} \times \{ 3 \times (-1) \} \times \{ 4 \times (-1) \} \times \{ 5 \times (-1) \} \)
\( =(2 \times 3 \times 4 \times 5) \times (-1) \times (-1) \times (-1) \times (-1) \)
\( =120 \times (-1) \times (-1) \times (-1) \times (-1) \)
\( =-120 \times (-1) \times (-1) \times (-1) \)
\( =120 \times (-1) \times (-1) \)
\( =-120 \times (-1) \)
\( =120 \)
これらのことから,
式の中に含まれる負の項が奇数個の場合,絶対値の積に「 - 」の符号をつける
式の中に含まれる負の項が偶数個の場合は,絶対値の積に「 + 」の符号をつける
ことになります。
この符号のつけ方を覚えておけば上の例のように \( -1 \) だけを取り出してかける必要がなくなるので
式を見ただけで自然に出てくるぐらいきっちり身につけておいてください。
\( -2 \times (-3) \times (-4) \times (-5) \) の場合,負の項が4個(偶数個)なので,商の符号は「 + 」になり,
\( -2 \times (-3) \times (-4) \times (-5)=+(2 \times 3 \times 4 \times 5) \)
\( =120 \)
と簡単に計算ができます。
正の数・負の数のわり算
ここでは,正の数・負の数のわり算について解説していきます。
かけ算のことを 除法(じょほう) ,わり算(除法)によって求められた結果を 商 と呼びます。
2つの数が同じ符号の場合は,絶対値の商に「 + 」の符号をつける
2つの数が異なる符号の場合は,絶対値の商に「 - 」の符号をつける
3つ以上の数のわり算の場合
式の中に含まれる負の項が奇数個の場合,絶対値の商に「 - 」の符号をつける
式の中に含まれる負の項が偶数個の場合は,絶対値の商に「 + 」の符号をつける
正の数 \( \div \) 正の数の場合
これは,算数で学んだなじみのあるわり算になります。
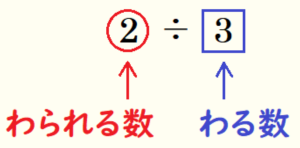
例として \( 2 \div 3 \) について考えてみます。
わり算はわる数を分母と分子をひっくり返した数のかけ算にできるので,
\( 2 \div 3=2 \div \dfrac{3}{1} \)
\( =2 \times \dfrac{1}{3} \)
\( =\dfrac{2}{3} \)
となります。
ちなみに,分母と分子をひっくり返した数を 逆数 と呼びます。
もとの数と逆数の積は必ず \( 1 \) になります。
例 \( \dfrac{2}{3} \) の場合
\( \dfrac{2}{3} \) の逆数は \( \dfrac{3}{2} \) になるので,
\( \dfrac{2}{3} \times \dfrac{3}{2}=\dfrac{2 \times 3}{3 \times 2}=\dfrac{6}{6}=1 \)
負の数 \( \div \) 正の数の場合
例として \( -2 \div 3 \) について考えてみます。
負の数を含む場合も正の数同士の場合と同じようにわる数の逆数をとることでかけ算として計算ができます。
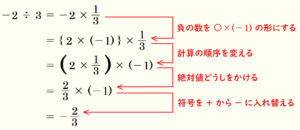
となります。
正の数 \( \div \) 負の数の場合
例として \( -2 \div 3 \) について考えると次のようになります。
負の数の逆数は,符号はそのままで絶対値の分母分子をひっくり返した数 になります。
例として \( -\dfrac{2}{3} \) の逆数について考えてみます。
もとの数と逆数の積は必ず \( 1 \) になるので,\( -\dfrac{2}{3} \) の逆数を □ とすると,
\( -\dfrac{2}{3} \times \) □ \( =1 \)
と表すことができます。
負の数に何かをかけた積が正の数になっているので,□は負の数であることがわかります。
また,もとの数の分子分母をひっくり返した数でもあるので,\( -\dfrac{3}{2} \) が逆数ということになります。
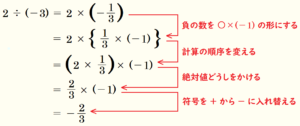
となります。
負の数 \( \div \) 負の数の場合
例として \( -2 \div 3 \) について考えると次のようになります。

正の数・負の数のわり算の結果をまとめると・・・
2つの数のわり算
負の数を含む場合も正の数同士の場合と同じようにわる数の逆数をとることでかけ算として計算ができます。
また、正の数の逆数は正の数,負の数の逆数は負の数で,符号が変わりません。
これらのことから,正の数・負の数のわり算の結果をまとめると次のようになります。

つまり,
2つの数が同じ符号の場合は,絶対値の商に「 + 」の符号をつける
2つの数が異なる符号の場合は,絶対値の商に「 - 」の符号をつける
ことになります。
3つ以上の数のわり算
先程の2つの数のかけ算のときと同じ考え方で負の数が3個の場合と4個の場合について符号がどのようになるか確認します。
● 負の項が3個の場合 (例:\( -2 \div (-3) \div (-4) \) )
\( -2 \div (-3) \div (-4)=-2 \times \left( -\dfrac{1}{3} \right) \times \left( -\dfrac{1}{4} \right) \)
\( =\{ 2 \times (-1) \} \times \left\{ \dfrac{1}{3} \times (-1) \right\} \times \left\{ \dfrac{1}{4} \times (-1) \right\} \)
\( =\left( 2 \times \dfrac{1}{3} \times \dfrac{1}{4} \right) \times (-1) \times (-1) \times (-1) \)
\( =\dfrac{1}{6} \times (-1) \times (-1) \times (-1) \)
\( =-\dfrac{1}{6} \times (-1) \times (-1) \)
\( =\dfrac{1}{6} \times (-1) \)
\( =-\dfrac{1}{6} \)
● 負の項が4個の場合 (例:\( -2 \div (-3) \div (-4) \div (-5) \) )
\( -2 \div (-3) \div (-4) \div (-5)=-2 \times \left( -\dfrac{1}{3} \right) \times \left( -\dfrac{1}{4} \right) \times \left( -\dfrac{1}{5} \right) \)
\( =\{ 2 \times (-1) \} \times \left\{ \dfrac{1}{3} \times (-1) \right\} \times \left\{ \dfrac{1}{4} \times (-1) \right\} \times \left\{ \dfrac{1}{5} \times (-1) \right\} \)
\( =\left( 2 \times \dfrac{1}{3} \times \dfrac{1}{4} \times \dfrac{1}{5} \right) \times (-1) \times (-1) \times (-1) \times (-1) \)
\( =\dfrac{2}{3 \times 4 \times 5} \times (-1) \times (-1) \times (-1) \times (-1) \)
\( =\dfrac{1}{30} \times (-1) \times (-1) \times (-1) \times (-1) \)
\( =-\dfrac{1}{30} \times (-1) \times (-1) \times (-1) \)
\( =\dfrac{1}{30} \times (-1) \times (-1) \)
\( =-\dfrac{1}{30} \times (-1) \)
\( =\dfrac{1}{30} \)
これらのことから,
式の中に含まれる負の項が奇数個の場合,絶対値の商に「 - 」の符号をつける
式の中に含まれる負の項が偶数個の場合は,絶対値の商に「 + 」の符号をつける
ことになります。
この符号のつけ方を覚えておけば上の例のように \( -1 \) だけを取り出してかける必要がなくなるので
式を見ただけで自然に出てくるぐらいきっちり身につけておいてください。
\( -2 \div (-3) \div (-4) \div (-5) \) の場合,負の項が4個(偶数個)なので,商の符号は「 + 」になり,
\( -2 \div (-3) \div (-4) \div (-5)=+(2 \div 3 \div 4 \div 5) \)
\( =+ \left( 2 \times \dfrac{1}{3} \times \dfrac{1}{4} \times \dfrac{1}{5} \right) \)
\( =+\dfrac{2}{3 \times 4 \times 5} \)
\( =\dfrac{1}{30} \)
と簡単に計算ができます。
かけ算とわり算が混じった計算
逆数をとってかけ算だけの式にしてから計算する
例として,\( 12 \div 4 \times 2 \div 3 \) の場合を考えてみます。
\( 12 \div 4 \times 2 \div 3=12 \times \dfrac{1}{4} \times 2 \times \dfrac{1}{3} \)
\( =\dfrac{12 \times 2}{4 \times 3} \)
\( =2 \)
特に整数だけの計算の場合,暗算で計算しがちですが,丁寧に分数の形で書き出して計算していくことをオススメします。
その理由は,わり算を含む場合は乗法の結合法則の使い方を間違えると計算結果が変わってしまうからです。
次に,乗法の結合法則の使い方を間違える典型例を示します。
95%の大人が間違える(らしい)! \( 9 \times 9 \div 9 \times 9=\;\boxed{ ? } \)
正解は \( 9 \times 9 \div 9 \times 9=\color{red}{81} \) です。
間違える人の中で多いとされている答えは \( 9 \times 9 \div 9 \times 9=\color{blue}{1} \) です。
これは,間違った形で結合法則を使って
\( 9 \times 9 \div 9 \times 9=9 \times 9 \div \color{blue}{(9 \times 9)} \)
\( =81 \div 81 \)
\( =1 \)
と計算しているからだと思われます。
乗法の結合法則が成り立つのはかけ算の部分だけなので,結合法則を使うのであれば
\( 9 \times 9 \color{red}{ \div 9} \times 9=9 \times 9 \color{red}{\times \dfrac{1}{9}} \times 9 \)
\( =9 \times 9 \times \left( \dfrac{1}{9} \times 9 \right) \)
\( =9 \times 9 \times 1 \)
\( =81 \)
としなければなりません。
暗算で計算できるため,さらっと計算しやすいところから計算してしまいがちですが,
丁寧に
\( 9 \times 9 \div 9 \times 9=9 \times 9 \times \dfrac{1}{9} \times 9 \)
\( =\dfrac{9 \times 9 \times 9}{9} \)
\( =81 \)
とすれば,計算間違いをしにくくなります。
負の数を含む場合は?
また,負の数を含む計算の場合には,かけ算だけ,わり算だけのときと同じように絶対値だけで計算をして式の中に含まれる負の数の個数に応じて「 + 」または「 ー 」の符号をつけることで値を求められます。
● 負の数が1個の場合 (例:\( 12 \div 4 \times 2 \div (-3) \) )
\( 12 \div 4 \times 2 \div (-3)=12 \times \dfrac{1}{4} \times 2 \times \left( -\dfrac{1}{3} \right) \)
\( =12 \times \dfrac{1}{4} \times 2 \times \left\{ \dfrac{1}{3} \times ( -1 ) \right\} \)
\( =\left( 12 \times \dfrac{1}{4} \times 2 \times \dfrac{1}{3} \right) \times ( -1 ) \)
\( =\dfrac{12 \times 2}{4 \times 3} \times (-1) \)
\( =2 \times (-1) \)
\( =-2 \)
● 負の数が2個の場合 (例:\( -12 \div 4 \times 2 \div (-3) \) )
\( -12 \div 4 \times 2 \div (-3)=-12 \times \dfrac{1}{4} \times 2 \times \left( -\dfrac{1}{3} \right) \)
\( =\{ 12 \times (-1) \} \times \dfrac{1}{4} \times 2 \times \left\{ \dfrac{1}{3} \times ( -1 ) \right\} \)
\( =\left( 12 \times \dfrac{1}{4} \times 2 \times \dfrac{1}{3} \right) \times (-1) \times (-1) \)
\( =\dfrac{12 \times 2}{4 \times 3} \times (-1) \times (-1) \)
\( =2 \times (-1) \times (-1) \)
\( =-2 \times (-1) \)
\( =2 \)
これらのことから,
式の中に含まれる負の数が奇数個の場合,絶対値の計算結果に「 - 」の符号をつける
式の中に含まれる負の数が偶数個の場合は,絶対値の計算結果に「 + 」の符号をつける
ことになります。


