正の数・負の数のたし算
算数で学んできたたし算は,答えが \( 0 \) または正の数の範囲に限られていました。
数学においては,負の数を含む場合についてのたし算を学んでいきます。
たし算のことを 加法(かほう) ,たし算(加法)によって求められた結果を 和 と呼びます。
数式の書き方のルール
負の数を扱うことによって,数式を書くときに新しいルールが追加されます。
その新しいルールは
「+」,「-」,「×」,「÷」の記号の後ろに書く数を符号をつけて表すときは必ずかっこをつける
です。
なぜかというと,
負の数を扱い始めたことによって「+」と「-」の記号は次の2つの意味を持つことになりました。
1.たし算・ひき算を表す記号
2.その数が正の数・負の数のどちらであるかを表す記号 → これが追加された
例えば,\( 2 \) と \( -3 \) のたし算をかっこを使わずに書くと \( 2+-3 \) となります。
この式だけを見たとき,「-」は上の1.2どちらの意味を表しているのかがわかりにくく,
1の意味で考える人と2の意味で考える人に分かれてしまう恐れがあります。
そこで,\( -3 \) という負の数を表している(2の意味である)ことをわかりやすく示すために
\( (-3) \) と書き,式は \( 2+(-3) \) と表します。
負の数が最初にくるときや正の数を符号をつけずに表す場合はかっこを省略できますが,
正の数を符号をつけて表す場合にはかっこが必要です。

正しい例 ・・・ \( 2+(-3) \),\( 3-5 \),\( 3-(+5) \),\( -4+2 \)
間違った例 ・・・ \( 2+-3 \),\( 3-+5 \),
正の数 \( + \) 正の数 のたし算
これは,算数で学んだなじみのあるたし算になります。
例として \( 2+3 \) について考えてみます。
「\( 2 \) に \( 3 \) を足した数」ということは,「\( 2 \) より \( 3 \) 大きい数」を表すので,
数直線を使って考えると
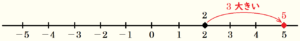
となります。
\( \color{green}{2}\color{red}{+}\color{blue}{3} \) を「\( \color{green}{2} \) から \( \color{red}{+} \) の方向に \( \color{blue}{3} \) 進んだ数」と考える方法もあるので,わかりやすい方で考えて大丈夫です。
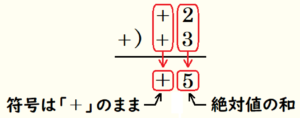
これを数直線を使わずに頭の中で計算すると,\( 2+3 \) は \( +2+(+3) \) と同じことです。
2つの数の符号は両方 \( + \) なので \( + \) のまま,絶対値は2つの数の絶対値の和になっています。
負の数 \( + \) 負の数 のたし算
例として \( -2+(-3) \) について考えてみます。
「\( -2 \) に \( -3 \) を足した数」ということは,「\( -2 \) より \( -3 \) 大きい数」を表しています。
「\( -3 \) 大きい数」は「\( 3 \) 小さい数」と言い換えることができるので,
「\( -2 \) より \( -3 \) 大きい数」は「\( -2 \) より \( 3 \) 小さい数」と同じことになります。
これを数直線を使って考えると,

つまり,\( -2+(-3)=-5 \) となります。
ちなみに,「\( -2 \) より \( 3 \) 小さい数」を数式で表すと,\( -2-3 \) となるので,
\( -2+(-3)=-2-3=-5 \) となります。
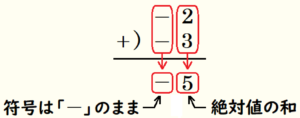
これを数直線を使わずに頭の中で計算すると,
2つの数の符号は両方 \( – \) なので \( – \) のまま,絶対値は2つの数の絶対値の和になります。
正の数 \( + \) 負の数 のたし算
例として \( 2+(-3) \) について考えてみます。
「\( 2 \) に \( -3 \) を足した数」ということは,「\( 2 \) より \( -3 \) 大きい数」を表しています。
また,「\( 2 \) より \( -3 \) 大きい数」は,「\( 2 \) より \( 3 \) 小さい数」といいかえることもできるので,
数直線を使って考えると

つまり,\( 2+(-3)=-1 \) となります。
ちなみに,「\( 2 \) より \( 3 \) 小さい数」を数式で表すと,\( 2-3 \) となるので,
\( 2+(-3)=2-3=-1 \) となります。
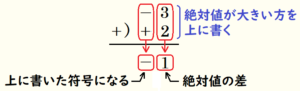
これを数直線を使わずに頭の中で計算すると,\( 2+(-3) \) は \( +2+(-3) \) と同じことであり,
符号は絶対値が大きい方の符号,絶対値は2つの数の絶対値の差になります。
負の数 \( + \) 正の数 のたし算
例として \( -2+3 \) について考えてみます。
「\( -2 \) に \( 3 \) を足した数」ということは,「\( -2 \) より \( 3 \) 大きい数」を表すので,
数直線を使って考えると

つまり,\( -2+3=1 \) となります。
これを数直線を使わずに頭の中で計算すると,\( -2+3 \) は \( -2+(+3) \) と同じことであり,
符号は絶対値が大きい方の符号,絶対値は2つの数の絶対値の差になります。
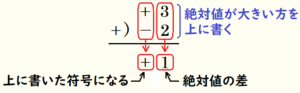
正の数・負の数のたし算の結果をまとめると・・・
正の数・負の数のたし算の結果についてまとめると次のようになります。

加法の交換法則と結合法則
加法の交換法則
たし算の式においては,たす順番を入れ替えても計算結果は等しくなります。
これを 加法の交換法則 といいます。
〇 \( + \) □ \( = \) □ \( + \) 〇
例として \( 2+(-3) \) と \( (-3)+2 \) について考えてみます。
● \( 2+(-3) \) の場合
\( 2+(-3) \) は,「\( 2 \) より \( -3 \) 大きい数」または「\( 2 \) より \( 3 \) 小さい数」なので,

● \( (-3)+2 \) の場合
\( (-3)+2 \) は,「\( -3 \) より \( 2 \) 大きい数」なので,
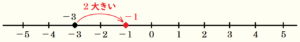
と,どちらも計算結果は \( -1 \) で等しくなります。
加法の結合法則
加法の交換法則より,たし算だけの式の場合,計算順序を入れ替えても計算結果は等しくなることから,
3個以上の数を足す場合に足す順番を入れ替えても計算結果は等しくなります。
これを 加法の結合法則 といいます。
\( ( \) 〇 \( + \) △ \( ) \; + \) □ \( = \) 〇 \( + \; ( \) △ \( + \) □ \( ) \)
ここから,
〇 \( + \) △ \( + \) □ \( = \) 〇 \( + \) □ \( + \) △
\( = \) △ \( + \) 〇 \( + \) □ \( = \) △ \( + \) □ \( + \) 〇
\( = \) □ \( + \) 〇 \( + \) △ \( = \) □ \( + \) △ \( + \) 〇
例として,\( 2+3+4 \) の場合を考えてみます。
\( 2+3 \) を先に計算する場合は,\( (2+3)+4=5+4=9 \)
\( 3+4 \) を先に計算する場合は,\( 2+(3+4)=2+7=9 \)
となり,どちらの計算方法でも和は \( 9 \) で等しくなっています。
また,以下のとおり,加法の結合法則は負の数を含んだたし算でも成り立ちます。
例として,\( 2+(-3)+4 \) の場合を考えてみます。
\( 2+(-3) \) を先に計算する場合は,\( \{2+(-3)\}+4=-1+4=3 \)
\( (-3)+4 \) を先に計算する場合は,\( 2+\{(-3)+4\}=2+1=3 \)
となり,どちらの計算方法でも和は \( 3 \) で等しくなります。
正の数・負の数のひき算
ここでは,正の数・負の数のひき算について解説していきます。
ひき算のことを 減法(げんぽう) ,ひき算(減法)によって求められた結果を 差 と呼びます。
正の数 \( – \) 正の数 のひき算
「引かれる数の絶対値が引く数より大きい場合」と「引かれる数の絶対値が引く数より小さい場合」にわけて考えます。
引かれる数の絶対値が引く数の絶対値より大きい場合
これは,算数で学んだなじみのあるひき算になります。
ちなみに,ひき算の式 ○ \( – \) □ の〇の部分にあたる数が引かれる数,□の部分にあたる数が引く数になります。
例えば,\( 3-2 \) の場合では,\( 3 \) が引かれる数,\( 2 \) が引く数になります。
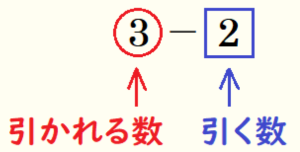
例として \( 3-2 \) について考えてみます。
「\( 3 \) から \( 2 \) をひいた数」ということは,「\( 3 \) より \( 2 \) 小さい数」を表すので,
数直線を使って考えると
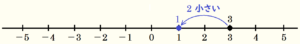
つまり,\( 3-2=1 \) となります。
引かれる数の絶対値が引く数の絶対値より小さい場合
例として \( 2-3 \) について考えてみます。
「\( 2 \) から \( 3 \) をひいた数」ということは,「\( 2 \) より \( 3 \) 小さい数」を表しているので,
数直線を使って考えると

つまり,\( 2-3=-1 \) となります。
これを数直線を使わずに頭の中で計算すると,
符号は必ず「\( \bf{-} \)」 になり,絶対値は2つの数の絶対値の差 になります。
ちなみに,「\( 2 \) より \( 3 \) 小さい数」は,「\( 2 \) より \( -3 \) 大きい数」といいかえることもできるので,\( 2-3=2+(-3)=-1 \) とあえてたし算に書き直して考えることもできます。
負の数 \( – \) 負の数 のひき算
「引かれる数が引く数より大きい場合」と「引かれる数が引く数より小さい場合」にわけて考えます。
引かれる数の絶対値が引く数の絶対値より大きい場合
例として \( -3-(-2) \) について考えてみます。
「\( -3 \) から \( -2 \) をひいた数」ということは,「\( -3 \) より \( -2 \) 小さい数」を表しています。
「\( -2 \) 小さい数」は「\( 2 \) 大きい数」と言い換えることができるので,
「\( -3 \) より \( -2 \) 小さい数」は「\( -2 \) 小さい数」は「\( 2 \) 大きい数」と同じことになります。
これを数直線を使って考えると,

つまり,\( -3-(-2)=1 \) となります。
ちなみに,「\( -3 \) より \( 2 \) 大きい数」を数式で表すと,\( -3+2 \) となるので,
\( -3-(-2)=-3+2=-1 \) となります。
これを数直線を使わずに頭の中で計算すると,
符号は必ず「\( \bf{-} \)」 になり,絶対値は2つの数の絶対値の差 になります。
引かれる数の絶対値が引く数の絶対値より小さい場合
例として \( -2-(-3) \) について考えてみます。
「\( -2 \) から \( -3 \) をひいた数」ということは,「\( -2 \) より \( -3 \) 小さい数」を表しています。
「\( -3 \) 小さい数」は「\( 3 \) 大きい数」と言い換えることができるので,
「\( -2 \) より \( -3 \) 小さい数」は「\( -2 \) より \( 3 \) 大きい数」と同じことになります。
これを数直線を使って考えると,

つまり,\( -2-(-3)=1 \) となります。
ちなみに,「\( -2 \) より \( 3 \) 大きい数」を数式で表すと,\( -2+3 \) となるので,
\( -2-(-3)=-2+3=1 \) となります。
これを数直線を使わずに頭の中で計算すると,
符号は必ず「\( \bf{+} \)」 になり,絶対値は2つの数の絶対値の差 になります。
正の数 \( – \) 負の数 のひき算
例として \( 2-(-3) \) について考えてみます。
「\( 2 \) から \( -3 \) をひいた数」ということは,「\( 2 \) より \( -3 \) 小さい数」を表しています。
「\( -3 \) 小さい数」は「\( 3 \) 大きい数」と言い換えることができるので,
「\( 2 \) より \( -3 \) 小さい数」は「\( 2 \) より \( 3 \) 大きい数」と同じことになります。
これを数直線を使って考えると,
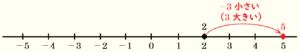
つまり,\( 2-(-3)=5 \) となります。
ちなみに,「\( 2 \) より \( 3 \) 大きい数」を数式で表すと,\( 2+3 \) となるので,
\( 2-(-3)=2+3=5 \) となります。
これを数直線を使わずに頭の中で計算すると,
符号は必ず「\( \bf{+} \)」 になり,絶対値は2つの数の絶対値の和 になります。
負の数 \( – \) 正の数 のひき算
例として \( -2-3 \) について考えてみます。
「\( -2 \) から \( 3 \) をひいた数」ということは,「\( -2 \) より \( 3 \) 小さい数」を表しているので,
これを数直線を使って考えると,
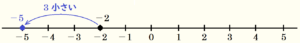
つまり,\( -2-3=-5 \) となります。
これを数直線を使わずに頭の中で計算すると,
符号は必ず「\( \bf{-} \)」 になり,絶対値は2つの数の絶対値の和 になります。
正の数・負の数のひき算の結果をまとめると・・・
正の数・負の数のひき算の結果についてまとめると次のようになります。

たし算とひき算が混じった計算
加法の交換法則、加法の結合法則より,たし算とひき算が混じった計算ではたし算だけをまとめて計算,ひき算だけをまとめて計算することができます。
〇 \( – \) △ \( + \) □ \( – \) ◇ \( = \) 〇 \( + \) □ \( – \) △ \( – \) ◇
\( = \) 〇 \( + \) □ \( -( \) △ \( + \) ◇ \( ) \)
例として,\( 5-4+3-2 \) の場合を考えてみます。
前から順番に計算する場合は,
\( 5-4+3-2=1+3-2 \)
\( =4-2 \)
\( =2 \)
たし算を先に計算する場合は,
\( 5-4+3-2=5+3-4-2 \)
\( =8-4-2 \)
\( =4-2 \)
\( =2 \)
となり,どちらの計算方法でも和は \( 2 \) で等しくなっています。
次に,ひき算の部分だけを考えると,
\( 5+3 \) の結果から \( 4 \) をひいて,さらに \( 2 \) をひく
つまり,\( 4+2=6 \) をひくと考えられるので,
ひき算の部分だけをまとめて計算して
\( 5-4+3-2=\color{red}{5}\color{blue}{-4}\color{red}{+3}\color{blue}{-2} \)
\( =\color{red}{5}\color{red}{+3}\color{blue}{-4}\color{blue}{-2} \)
\( =\color{red}{5}\color{red}{+3}\color{blue}{-(4+2)} \)
\( =\color{red}{8}\color{blue}{-6} \)
\( =2 \)
とすることもできます。
また,負の数を含む計算の場合には,次の法則で符号を変えてかっこを使わない式に直すと計算しやすくなります。
符号のかえ方は次のとおりです。

例として,\( 5-4+(-3)-(-2) \) の場合を考えてみます。
上の法則にしたがって符号を変えると,
\( 5-4+(-3)-(-2)=5-4-3+2 \)
\( =5+2-4-3 \)
\( =5+2-(4+3) \)
\( =7-7 \)
\( =0 \)
となります。


